非完美CSI情况下大规模MIMO系统的下行链路能效优化

禹永植, 张春红, 郝 海

(1. 哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001;2. 北京遥感设备研究所, 北京 100854)

0 引 言

近年来,绿色通信一直是通信领域的热点问题,能源消耗和不断增长的业务需求之间的矛盾将长期存在,学者们对节能和绿色能源的注重也推动着无线通信技术的发展,在之前技术的基础上,第五代移动通信系统(the 5th generation mobile communication systems, 5G)应运而生[1-2]。5G的系统模型架构和其关键技术自然成为了国内外学者所关心的热点问题,作为5G的关键技术之一的大规模多输入多输出(multiple input multiple output, MIMO)通过在基站处配置数十乃至数百根天线来实现更高的频谱效率[3],但在实际通信环境中,大量配置天线的做法会导致更高的功率损耗,这对我们所倡导的绿色通信的理念相违背[4]。因此,大规模MIMO系统中对于能效问题的研究非常重要。

蜂窝系统吞吐量的大幅度增加需要通过密集网络来实现[5],这种密集网络一般有两种技术方法实现:微小区网络和大规模MIMO系统[6]。前者通过配置微型小区的网络来实现降低传输损耗的目的,但其使用更多的硬件电路从而大量增加功率损耗[7-10],而后者利用复用技术通过增加基站天线数来为更多的用户提供服务,同样会增加功耗[11-13]。一般来讲微小区网络随着密度增加,得到的增益会逐渐趋于平稳,所以可以通过将其与大规模MIMO结合来得到更好的吞吐量优化,但二者都会以增加功耗的代价来达到更高的吞吐量,因此只有当代价与收益取得平衡时,才可以最大化能量效率[14]。文献[15]考虑了将微小区与大规模系统技术相结合，采用随机几何方法建模，设计了一个蜂窝网络来实现最大化能量效率,提出了电路功耗模型，从而得到一个更符合实际生活的能量效率优化问题,但由于只考虑了单小区环境,没有考虑到多小区中的小区间干扰，从而影响了整个系统下的MIMO能效性能,并且对非完美信道状态信息(channel state information, CSI)情况下的研究甚少。文献[16]考虑了密集网络和大规模MIMO等技术结合得到异构网络(Hetnet)来对能量效率进行优化,但只对上行链路进行了研究分析,目前大多数文章都只研究了上行链路的能效问题,缺少了对下行链路中能效优化的研究。

针对上述问题,本文设计了一种非完美CSI情况下能实现能量效率最大化的多小区大规模MIMO系统下行链路的实现方法。首先,利用随机几何方法建立大规模MIMO系统的下行链路系统模型[17-20],系统模型中基站密度按λ的均匀泊松点分布,用户则根据基站进行随机分布。其次,在系统模型中引入实际通信系统中导频复用系数、下行传输的固定比例、硬件损伤程度等参数,通过数学公式推导出包含基站的天线数、用户数、基站密度、导频复用系数以及功率控制因子等参量的下行链路的信干噪比(signal to interference plus noise ratio, SINR)表达式从而得到频谱效率。然后,将能量效率设定为区域性质,考虑区域内发射功率、硬件损耗、信号处理[21-23]等各种情况下能耗的功耗模型,由此得到能效方程。最后通过交替迭代的优化算法[24]进行能效优化并得到在最大化能效时的各个参数的数值。仿真实验表明,相比于现有的多小区实现方法,本文所提的下行链路实现方法在有效提升了大规模MIMO系统能效的同时还对环境变化有了更强的鲁棒性,具有更实际的应用场景。

1 系统模型及能效分析

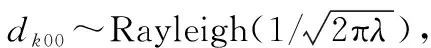
(1)

(2)

在下行传输过程中,用户端k接收到的来自BS0的信号[28]可表示为

(3)

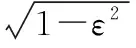
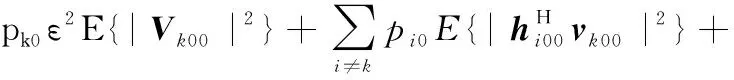
(4)

我们假设在用户端使用MRC接收技术来进行数据恢复,根据MRC接收技术得到下行链路平均频谱效率的下界

(5)

本文研究多小区的下行链路的能量效率,能量效率定义为每单位能量传输的信息量[30],数学表达式为

(6)

其中,单位区域内的平均频谱效率为UTP=λK·SE。单位区域内的功率消耗为发射功率、硬件方面损耗、信号处理、回程信号和各种实际情况下的损耗等因素的模型。单位区域的总功耗为

(7)

式中:η为下行线性功率放大器效率;C0为一个基站的静态功率损耗;C1K为用户端的功率损耗;D0M为基站传输链路的功率损耗;D1MK为用户和基站的信号处理功耗;A为编、解码及回程信号所需的功率损耗。

本文通过设定不同的模型符号长度S、传播衰减指数(α,ω)、硬件及传输环节中的能量消耗(η,ε,C0,C1,D0,D1)得到最大能效时的优化参数θ=(β,ρ,λ,K,M)。将上述参数引入到优化函数中,优化问题目标函数为能量效率,约束条件为导频复用系数、功率控制因子以及基站密度的约束。多小区下行大规模MIMO系统的能效优化问题描述为

(8)

式中：Θ代表所有能效值点包含的参数取值；1≤β≤S/K代表导频系数的上下限；功率控制因子ρ为非负；基站密度λ也为非负。

2 交替迭代优化算法

首先,将SINR的数学表达式改写为以β为参数的表达式

(9)

其中,

(10)

其中,

(11)

式中:CD为C0+C1K+D0M+D1MK的简写表达;q(γ)为式(10)中的B1γ/M(1-ε2)2-B2γ;R为log2(1+γ)。

然后,优化基站天线数M和用户数K,把优化得到的λ和ρ代入目标方程,得到

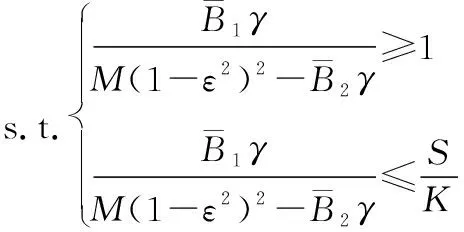
(12)

其中,

EE∞可表示为

(13)

为了后续分析方便,本文将基站的天线数M替换为每个用户端的基站天线数c=M/K。可知式(13)是拟凹函数,可以通过求一阶导数得到最优用户数K*为

(14)

其中,

(15)

把EE∞改写为参数为c的表达式:

将过去自然菌种发酵发展成为筛选菌种纯种发酵，专注于北京传统食品腐乳、臭豆腐、芝麻酱等百余品种生产的北京王致和食品集团有限公司运用科技工艺，将35道传统发酵豆制品工序实现现代化传承，让罐装腐乳走进千万百姓家。好想你健康食品股份有限公司则在枣片生产上灵活应用酶解技术、微细化技术和微波干燥技术，解决了枣片口感粗糙、干燥时间长等技术难题。中粮集团成立营养健康研究院，将科技融入食品开发，生产出一系列膨化食品，如悦活燕麦片、悦活蜂蜜、美滋滋花生及花生酱、美滋滋软糖巧克力、美滋滋膨化谷物卷、中宏营养早餐粉、番茄沙司等。

(16)

上述公式是拟凹函数,可以通过求一阶导数得到最优解c*,表达式为

(17)

其中,

(18)

(19)

a2=(1-ε2)(1-(1+γ)ε2)

(20)

(21)

a4=C0+C1K

(22)

a5=D0K+D1K2

(23)

综上所述,能效优化问题的交替迭代算法过程如下所示。

步骤 1初始化。令迭代次数t=1,0<ξ<1,并设定θ=(K,M)的可行起始点。

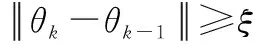
步骤 3再固定K计算M,后令t=t+1。

步骤 4重复步骤2和步骤3,对θ=(K,M)进行更新,直到达到收敛,返回一组最大化能效的(K,M)值。

3 仿真实验与结果分析

为了验证本文所提的多小区下行大规模MIMO的能效优化的性能,本文采用蒙特卡罗进行仿真分析。本文选择文献[7]与本文所提下行链路方法采用相同的交替优化算法的能效性能进行比较验证。

3.1 仿真参数配置

考虑多小区大规模MIMO通信系统有K个用户随机分布其中,相干块长度S=400,系统带宽为B。假设所有用户的最大允许发送功率和回路能耗均相同,系统所有噪声功率均是功率谱密度相同的高斯白噪声。大规模MIMO系统的具体参数如表1所示。

表1 大规模MIMO系统参数设置

3.2 可行性

系统能效随基站密度λ变化的曲线如图2所示,图中BS表示基站个数。

EE作为基站密度λ的函数,根据每个给定的λ值对其他优化变量进行优化。EE的下界都是使用平均SE公式计算得到的,上界则是通过蒙特卡罗模拟得到。首先,图2考虑了3种不同的SINR情况分别为SINR=2、3、4,3种情况下上界与下界之间都只有一个很小的差距并且当γ变大时,差距随之减小。这验证了本文提供的SE表达式的准确性。其次,通过增加λ可以极大地改善EE,这也说明了本文所提方法可以最大限度地优化EE。但是,基站密度增加带来的增益在λ=10到λ=100的区间内趋于饱和,这说明一味地增加λ也不能提高EE。最后,图中可以看出EE随着γ的增加而减少,这也说明了只提高SE不能整体增加能效。

系统能效随基站密度λ与导频复用系数β变化的曲线如图3所示。

仿真中设置大规模MIMO的基站天线数与用户数为100和10,利用蒙特卡罗方法进行模拟仿真,可以看出EE在相同导频复用系数下随λ先在20以内增大后一直趋于平稳。这也再次验证了增加基站密度可以使EE更大限度地改善。EE在基站密度相同时随导频复用系数也是先增大后平稳的趋势,可以得出合适的导频复用系数也会得到更大的EE。

3.3 性能分析

本文进一步研究了用户数与基站天线数对EE的影响,如本文第2节所述,交替优化算法得到的仿真结果如图4、图5所示。

初始化点均设置为(K,M)=(1,20),由图2可以看出,SINR=3时处于3种情况下能效中间位置,更具有一般性,因此,后续SINRγ均设定为3。从图4为文献[7]中能效随K、M的变化,图5为本文提出的下行大规模MIMO的能效方程得到的EE随K、M的变化。图4可以看出现有方法经过数次迭代后得到优化解(K*,M*)=(3,78),能效最大值为4.1。计算得出图4M/K=26,最优解符合大规模MIMO天线设定。图5可以看出本文方法经过数次迭代后得到优化解(K*,M*)=(11,113),能效最大值为4.6。计算得出图4M/K≈10,最优解同样符合大规模MIMO天线设定。与文献[7]相比,本文所提方法在EE数值上有了12.2%的提升,验证了本文方法不仅能有效提升能量效率，并且明显看出图5相比图4曲面更加平缓,验证了在环境发生改变时本文所提方法具有更强的鲁棒性,更具有实际意义。

如图6所示为系统能效在SINR为3的情况下随用户密度变化的曲线图,UE表示用户个数。设定M和K为图5仿真中得到的最优解M=113和K=11。由于用户是按基站的分布而随机分布,所以可以得到用户密度与基站密度存在比例关系,通过图6可以看出,在用户密度为100左右时交替优化算法可以迭代出最优天线数和用户数。

由此可以得到如下几个结论:首先,当用户密度足够大时,EE独立于用户密度;其次,本文优化算法迭代得到的M和K与仿真设定的M=113和K=11在用户密度达到一定数值时就可保持一致,验证了在用户密度达到一定程度时通过交替迭代优化算法就可以使能效最大化,这也意味着本文所提方法在优化能效的问题上可以得到很好的结果。

4 结 论

本文研究了非完美CSI下多小区大规模MIMO系统中下行链路的能效问题,首先推导出大规模MIMO系统中非完美CSI情况下包含基站天线数、导频复用因子、用户数量以及发射功率等参数的最大能效方程,并通过交替迭代优化算法求解出各参数的最优解。经仿真验证,本文所提下行链路实现方法具有良好的收敛性和可行性,可以实现能效优化,仿真得到的基站天线数与用户数符合大规模MIMO系统的天线设置,且与文献[7]中多小区下行链路能效相比,在能量效率方面也具有明显优势,数值方面相比文献[7]提升了12.2%左右,并且在环境发生改变时本文所提方法具有更强的鲁棒性,在实际情况中也具有代表性。