高速低复杂度可重构L&R算法研究与实现

胡婉如, 王竹刚, 梅如如, 陈 轩

(1. 中国科学院国家空间科学中心复杂航天系统电子信息技术重点实验室, 北京 100190;2. 中国科学院大学电子电气与通信工程学院, 北京 100049)

0 引 言

随着空间探测任务的日益繁重,对有效载荷系统数传速率提出了更高的要求,高速数传系统研究也迫在眉睫。由于多普勒频移和收发两端本振时钟偏差等因素,接收机采集的信号存在频率偏移和相位偏移,需通过载波恢复算法进行补偿。载波恢复算法是数传接收机关键技术之一,其性能直接决定了数传接收机的准确性和可靠性。载波恢复包括载波频偏恢复和载波相位恢复两步。载波频偏恢复算法和载波相偏恢复算法可分为数据辅助(data aided, DA)和非DA(not DA, NDA)两大类。载波频偏恢复算法对接收数据的频偏进行补偿,并将剩余频偏和剩余相偏减至载波相位恢复算法可纠正范围。

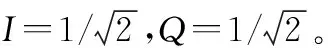
为提高算法精度,采取基于多段导频自相关函数叠加的改进L&R算法。为平衡载波频偏估计范围和算法精度,先采用高速低复杂度可重构L&R算法=2的架构将大载波频偏补偿至较低范围,再切换至=17的架构,使锁定后的频偏补偿保持在高精度。为便于算法逻辑架构实现与提高算法可工作时钟速率,对自相关函数公式进行分解和优化,实现了各函数功能模块化,并在优化后的自相关函数架构的基础上进一步提高L&R算法精度,最终提出一种高速低复杂度可重构L&R算法及其架构。仿真结果表明,本文提出的高速低复杂度可重构L&R算法可满足载波同步算法解调性能,且与理论误码率曲线基本一致;提出的算法架构可减少92.59%的乘法器;工作时钟频率高达370.37 MHz,可满足高速数传需求。

1 载波频偏恢复

1.1 载波频偏估计算法

假设信号经过下变频并已经取得符号定时同步,则接收信号的表达式为

()=ej(2πΔ+Δ)+

(1)

式中:为发送机在时刻发送的符号;Δ为信号的频偏;Δ为信号的相偏;为高斯白噪声;为符号速率。

(2)

()的自相关函数()表达式为

(3)

式中:1≤≤-1,为导频符号的个数,=36。

Kay频偏估计算法的表达式为

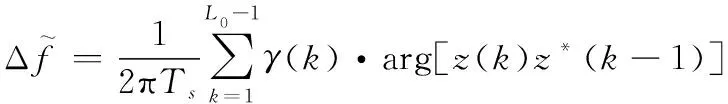
(4)

式中:=1,2,…,-1;加权系数()为

C&S频偏估计算法的表达式为

(5)

式中:=1,2,…,-1。

M&M频偏估计算法的表达式为

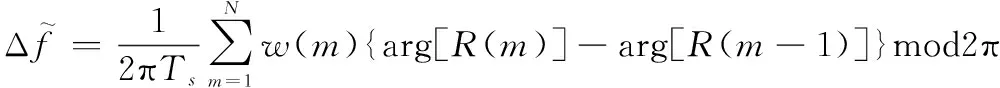
(6)

式中:1≤≤;加权系数()为

Jiang频偏估计算法的表达式为

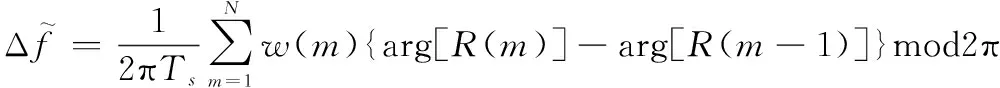
(7)

式中:1≤≤;加权系数()为

Fitz算法的表达式为

(8)

L&R算法的表达式为

(9)

为提高载波频偏恢复算法的精度,对Kay、C&S、M&M、Jiang、Fitz和L&R算法进行分析与最优参数筛选。Kay、C&S、M&M、Jiang、Fitz和 L&R 6种频偏估计算法的理论频偏估计范围如表1所示,其中Kay算法、C&S算法、M&M算法和Jiang算法的理论频偏估计范围只与符号速率有关,最大可估计0.5倍符号速率的频偏;Fitz算法和L&R算法的理论频偏估计范围与符号速率和参数有关,最大只能估计1符号速率的频偏,越大,频偏估计范围越小,精度越高,因此常用于小频偏算法恢复。

表1 不同频偏估计算法的理论频偏估计范围

在调制方式为16APSK,码长为8 160,信噪比分别为5 dB、10 dB、15 dB、20 dB,不同参数下的L&R算法和Fitz算法均方根误差性能仿真如图1所示。由图1可知,相比于Fitz算法,L&R算法性能更加稳定,本文对L&R算法进行载波频偏恢复方案的改进。

图1 参数N对L&R和Fitz算法频偏估计性能影响Fig.1 Influence of parameter N on the performance of L&R and Fitz algorithm frequency offset estimation

1.2 高速低复杂度可重构L&R算法

(10)

(11)

令

(12)

式中:1≤≤-1,0<≤,则

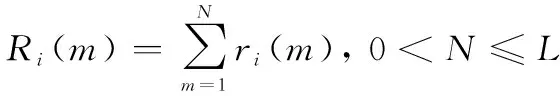
(13)

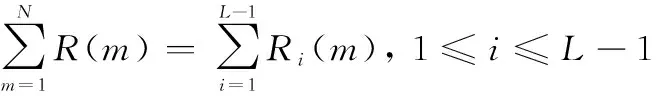
(14)

则有

(15)

由式(12)可知,进行相同间隔自相关计算的去调制信号均可复用同一间隔子自相关模块,图2为间隔为的子自相关函数模块框图。由式(13)～式(15)可知,复杂的去调制导频段自相关函数功能被完全分解成不同间隔子自相关函数,便于模块化设计。

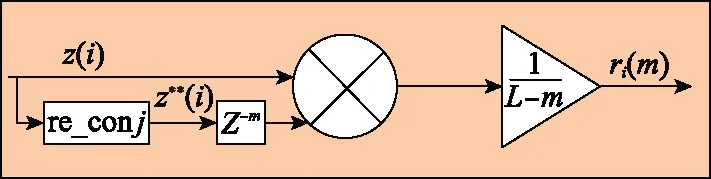
图2 子自相关函数模块Fig.2 Sub-autocorrelation function module

此外,可叠加连续个导频块的自相关值进行平均提高L&R算法估计精度性能,相应表达式为

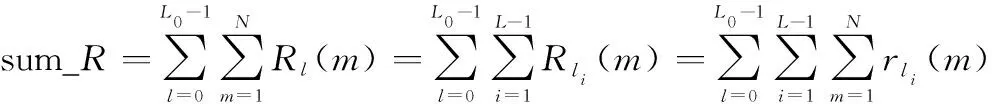
(16)

式中:sum_为多段连续导频段自相关函数累加值;()为第个导频段自相关函数;()为第个导频段的第个去调制信号不同间隔自相关值和;()为第个导频段的第个去调制信号间隔为的自相关值。

高速低复杂度可重构L&R算法的表达式为

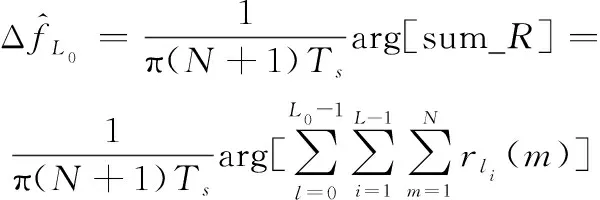
(17)

式中:1≤≤。由式(16)和式(17)可知,可根据不同参数选择不同间隔子自相关函数模块进行累加,灵活重构具有不同频偏估计范围的L&R算法架构。其中,当叠加导频段自相关函数段数为时,清除自相关导频段累加器累计值,等待下次累加开始。

2 载波频偏恢复算法实现

2.1 载波频偏估计与载波同步整体结构

由文献[14,16-22]可知,常规的载波同步方案可分为3步,包括载波粗频偏恢复、载波细频偏恢复和载波相位恢复,较为复杂。本文基于高速低复杂度可重构L&R算法和导频辅助相位线性插值算法进行载波同步方案设计,具体载波同步框图如图3所示,主要包括帧同步、载波频偏恢复和载波相位恢复3部分。帧同步采用SOF+PLSC(start of frame and physical layer signaling code)联合差分相关检测算法检测帧头位置,再由帧头位置推算出导频段位置、导频段间距和构建数据位置索引;载波频偏恢复根据导频段数据利用高速低复杂度可重构L&R算法计算出频偏,并通过环路滤波器和数控振荡器(numerically controlled oscillator, NCO)进行频偏补偿;最后根据导频段间距和数据位置索引利用导频辅助相位线性插值算法推算当前数据相偏,进行相位恢复,其中频偏恢复算法采用反馈结构,相位恢复算法采用前馈结构。载波频偏估计算法的准确性直接决定了传输信息的有效性和可靠性,环路滤波器的设计有利于提高系统的抗干扰性能。

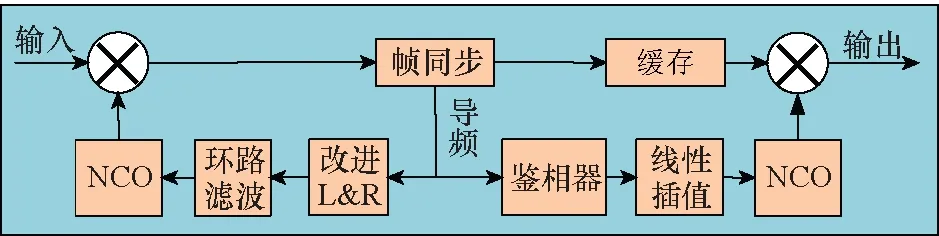
图3 载波同步框图Fig.3 Carrier synchronization block diagram

2.2 载波频偏估计算法结构

如式(10)、 式(12)～式(14)所示,自相关公式分解后的每个公式可进行模块化设计。式(12)可以设计成导频段自相关函数的子模块,如图2所示,该子模块具有普遍性和可复用性,便于不同频偏估计范围的L&R算法重构。式(14)和式(16)均涉及数据累加,可合理使用累加器,简化自相关函数累加计算框架结构,减少累加过程的时延。如图4所示,自相关函数实现可由Unit1、Unit2和Unit3 3部分组成,其中 Unit1对应实现第个去调制符号不同间隔的自相关(),Unit2对应实现不同间隔自相关值累加(),Unit3对应实现整个导频段自相关值累加()。图4中en36表示导频段36个数据符号有效信号,pilot_en表示导频段最后一个符号数据有效。

如图5所示,将多个导频段的自相关值()进行叠加,可由Unit4实现,当pilot_en有效时,累加器使能,自相关值进行累加,当叠加导频段自相关函数段数为时,计算频偏估计值,并清除累加器累计值,等待下次累加。由Unit4可知,其资源增加有限。

图4 自相关函数框图Fig.4 Block diagram of autocorrelation function

图5 多段导频自相关值叠加求频偏框图Fig.5 Block diagram of multi-segment pilot autocorrelation value superposition for frequency offset calculation

由图4和图5可知,对于不同参数的差异在于不同间隔子自相关函数模块()叠加个数,叠加不同数量导频段自相关函数在于参数的修改,因此高速低复杂度可重构L&R算法架构的修改是简单清晰的。 其中enable()指示间隔为的子自相关函数模块输出是否参与计算,当=时,enable(1),enable(2),…,enable()有效,其余使能信号无效,使能信号的控制使得算法可灵活根据需求进行重构。

2.3 环路滤波器结构

高速低复杂度可重构L&R算法根据连续个导频块累加自相关值计算频偏,并通过反馈环路进行载波频偏恢复,其中载波同步环路滤波器采用可降采的环路滤波结构。如图6所示,可降采的环路滤波结构可由Unit5和Unit6两部分组成,Unit5对应实现积分清除滤波器(integrate dump filter, IDF),Unit6对应实现二阶有源比例积分滤波器。积分清除滤波器可抑制高频噪声、降采,结构简单。环路滤波器可平滑误差值,减小噪声和抖动的影响,使环路调整更加稳定。其中,环路滤波器的递归方程为

()=[(-1)-(-1)]+()+()

(18)

式(18)可简化为

()=(-1)+()+()

(19)

式中:()为积分清除滤波器输出;()为二阶环路滤波器输出;()=()-(),且()为第二支路输出。

式中:为环路带宽;=0707;为鉴相器增益系数;为数控振荡器增益系数;为符号周期。

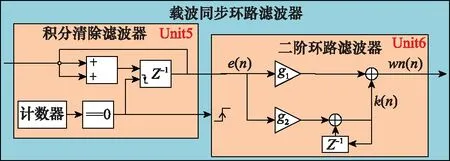
图6 载波同步环路滤波器Fig.6 Carrier synchronous loop filter

3 载波同步仿真与硬件实现

为验证高速低复杂度可重构L&R算法的性能,根据表2所示仿真参数对高速低复杂度可重构L&R算法进行仿真,载波同步仿真的流程如图7所示。首先采用SOF+PLSC联合差分检测算法检测帧头,推算导频段位置,然后利用高速低复杂度可重构L&R算法估算载波频偏,并进行载波频偏恢复,将剩余频偏和剩余相偏减至导频辅助相位线性插值算法可纠正的范围,最后经过解映射,计算误比特率。

表2 载波频偏恢复算法仿真参数

图7 载波同步仿真流程图Fig.7 Carrier synchronization simulation flowchart

3.1 高速低复杂度可重构L&R算法仿真及性能分析

由图1可知,随着越大,L&R算法精度越高,且当≥17后,均方根误差性能改善比较有限。由表1可知,可捕获理论载波频偏为符号速率的1(+1),随着越大,L&R算法可捕获频偏范围越小,其中=2的架构最高可补偿理论载波频偏为符号速率的13,=17的架构最高可补偿理论载波频偏为符号速率的118。此外,随着越大,高速低复杂度可重构L&R算法资源消耗越高,而切换过程只需控制使能信号即可,不会额外增加资源消耗,且资源消耗取决于最终切换到的精度更高的架构。如果可重构L&R算法精度不足以将剩余频偏和剩余相偏减至导频辅助相位线性插值算法可纠正的范围,那么无法正确进行载波同步。因此,为平衡载波频偏估计范围、算法精度、资源消耗等因素,本文先采用高速低复杂度可重构L&R算法=2的架构将载波频偏快速补偿至较低范围,再切换至=17的架构,使得锁定后的频偏补偿保持在高精度。高速低复杂度可重构L&R算法架构具有极高的可重构性和灵活性,可根据不同应用场景选择合适参数进行载波频偏恢复。

为进一步确定高速低复杂度可重构L&R算法最优性能参数,结合表2所示的仿真条件,在8 dB信噪比和不同叠加导频段自相关函数段数下,对高速低复杂度可重构L&R算法的频偏估计性能进行仿真。由图8可知,当=1时,未进行导频段自相关叠加的高速低复杂度可重构L&R算法的均方根误差较高,所选叠加导频段数为16～64时,其均方根误差性能几乎相同。当=32时, 高速低复杂度可重构L&R算法均方根误差性能最佳,算法精度有所提升。

图8 叠加段数L0对高速低复杂度可重构L&R算法频偏估计性能影响Fig.8 Influence of the number of overlaps L0 on the performance of the high-speed, low-complexity, reconfigurable L&R algorithm frequency offset estimation

在信噪比为20 dB时,对应无载波同步和载波同步后的16APSK信号星座图如图9所示。

图9 载波同步前后16APSK信号星座图Fig.9 16APSK signal constellation diagram before and after carrier synchronization

由图9可知,载波同步前星座图受频偏和相偏的影响,无法准确识别星座点,这对接收机的解调性能提出了极大的挑战;载波同步后,剩余频偏和剩余相偏的影响极其有限,星座点分布清晰,便于接收机的解调。结合表2所示仿真条件和图3所示载波同步结构,在不同的信噪比条件下,进行载波同步仿真,得到如图10所示载波恢复算法误比特率曲线。由图10可知,载波恢复算法误比特率曲线和理论误比特曲线几乎重合,性能损失很小,且在23 dB时,误码率已降为0。可知高速低复杂度可重构L&R算法满足高速接收机跟踪锁定精度和解调性能的需求。

图10 载波同步算法误比特率曲线Fig.10 Bit error rate curve of carrier synchronization algorithm

文献[15]中先采用D&M(Delay & Multiply) (=2)进行了载波粗频偏恢复,再采用L&R算法(=9)进行载波细频偏恢复;文献[16]中提出的常规载波恢复方案是先采用D&M(=2)进行了载波粗频偏恢复,再采用L&R算法(=18)进行载波细频偏恢复;文献[16]中提出的改进方案是先采用M&M算法(=9)进行载波粗频偏恢复,再采用简单导频块相关算法进行载波细频偏恢复。以往文献中整个频偏恢复方案是比较复杂的,而本文所用的可重构L&R算法,可先用=2的L&R算法架构将载波频偏快速跟踪锁定至较小频偏范围,再利用=17的架构进行精度更高的锁定,整个过程只需使用可重构L&R算法,且只需控制使能信号即可实现对应的架构,资源消耗也只取决于=17的架构。

文献[15]和文献[16]中关于L&R载波频偏估计算法和M&M载波频偏估计算法的计算复杂度如表3所示。对应不同算法,乘法器资源消耗均较多,而本文提出的改进结构相比于直接结构乘法器消耗减少了92.59%,极大地节省了资源消耗。此外,由表1可知, L&R算法的参数取值越大,计算复杂度越高,频偏估计范围越小,精度越高。本文高速低复杂度可重构L&R算法及其架构先基于=17的架构进行设计,当载波频偏较大时,控制使能信号,让架构先以=2的情况进行载波频偏补偿,当载波频偏补偿至剩余频偏小于5 kHz时,控制使能信号,让架构以=17的情况进行载波频偏补偿,直至环路锁定。高速低复杂度可重构L&R算法及其架构可兼顾计算复杂度和算法精度,适用于高速接收机中,具有极高的应用价值。

表3 不同载波频偏估计算法计算复杂度对比

3.2 高速低复杂度可重构L&R算法实现性能分析

本文基于XCKU040-FFVA1156-2-E硬件平台进行硬件实现,开发环境为Vivado2017.4,载波频偏恢复仿真结果如图11所示。freq_ini和freq_inq为载波频偏恢复算法输入信号的实部和虚部信号;en36指示导频段符号数据有效, 其中导频段符号个数为36;pilot_en指示导频段最后一个符号数据有效;freq_cos_outi和freq_cos_outq分别为用于补偿载波频偏的实部、虚部信号。当en36有效时,可重构L&R算法根据导频段符号数据进行频偏估计,将估计出的频偏信号送入NCO模块,得到freq_cos_outi和freq_cos_outq,并将freq_cos_outi和freq_cos_outq用于频偏补偿。指示当前工作架构情况,先用=2的架构将载波频偏快速跟踪锁定至5 kHz,然后将可重构L&R算法架构切换至=17的架构,使得剩余频偏和剩余相偏减至导频辅助相位线性插值算法可纠正的范围,从而正确实现载波同步。

图11 载波频偏恢复仿真结果Fig.11 Carrier frequency offset recovery simulation results

高速低复杂度可重构L&R算法的资源消耗和可工作时钟频率如表4所示。其中，LUT、FF和BRAM分别表示为查找表(look up table, LUT)、触发器(flip-flop, FF)和块随机存储器(block random access memory, BRAM)。高速低复杂度可重构L&R算法在XCKU040-FFVA1156-2-E上可工作时钟频率高达370.37 MHz，数字信号处理器(digital signal processor, DSP)资源仅消耗了3.54%，实现了硬件资源和可工作时钟之间的平衡。现有的L&R载波频偏恢复算法主要基于低速数传系统进行研究与实现，不适用于高速数传系统，本文提出的高速低复杂度可重构L&R算法及其架构适用于高速数传系统，在高速接收机中具有极高的应用价值。

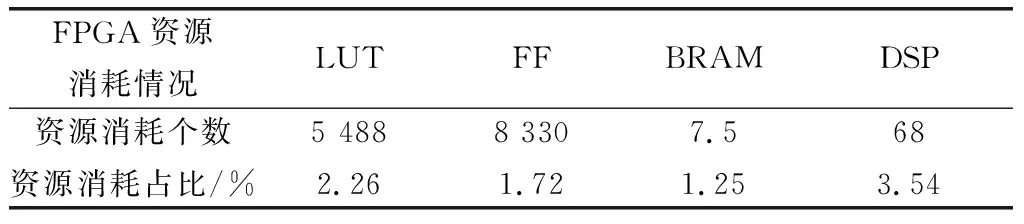
表4 高速低复杂度可重构L&R算法的资源消耗

4 结 论

为简化和模块化载波频率恢复算法的实现结构,提高载波频率恢复算法精度和可工作时钟频率,本文提出一种高速低复杂度可重构L&R算法及其架构。首先对L&R算法的自相关公式进行分析、分解,并对分解后的公式进行模块化设计;然后基于模块化的自相关函数架构进行设计,合理使用累加器、简化整个框架结构、减少时延;最后利用叠加多个导频段自相关函数提高算法精度。结果表明,载波同步后的误比特曲线与理论误比特率曲线几乎重合,性能损失较小;优化后的结构实现简单,乘法器消耗可减少92.59%,可工作时钟频率高达370.37 MHz。本文提出的L&R算法架构具有可重构性,可灵活应用于不同载波频偏场景,相较于传统接收机,可应用于高速数传系统中。接下来将对可重构L&R算法的架构进行进一步的优化,减少资源消耗。