基于强化学习的全电推进卫星变轨优化方法

韩明仁, 王玉峰,*

(1. 北京控制工程研究所, 北京 100094; 2. 空间智能控制技术重点实验室, 北京 100094)

0 引 言

全电推进卫星目前主要应用于地球同步轨道(geostationary orbit, GEO)相关任务中,使用电推力器实现全部的轨道转移、位置保持、角动量卸载等功能。得益于电推力器的高比冲和高燃料利用率,全电推进卫星能够搭载更多的有效载荷。然而,全电推进卫星由于推力小,依靠电推力器点火进入GEO的时间要长达几个月或半年多的时间。因此,优化变轨策略,缩短变轨时间,是全电推进卫星研究中的关键问题之一。

全电推进卫星轨道优化问题属于最优控制问题的范畴,本文主要研究全电推进卫星在转移轨道段以时间最优为目标的变轨策略优化方法,初始轨道为星箭分离后的同步转移轨道(geostationary transfer orbit,GTO),目标轨道为GEO。该问题要求在满足系统约束和动力学约束的前提下,在整个转移过程中确定一个推力方向变化策略。高度非线性和非凸动力学、空间环境摄动以及局部极小值的存在使优化过程十分复杂。连续小推力变轨问题目前已存在的研究成果主要包括解析方法和数值方法两大类。解析方法通过理论推导获得最优轨道的解析解,但对于大多数航天器的轨道优化问题,可行性得不到保证。大多数研究者都致力于数值方法的研究,如直接法、间接法、反馈控制法等。直接法的基本思想是将控制变量离散化,使最优控制问题转化成一个非线性规划问题,然后使用现有的优化方法对其进行求解,Ricciardi等采用结合有限元素全局多目标优化方法、启发式的进化算法以及基于梯度的约束非线性规划方法开发了用于空间系统任务设计、优化的多目标直接混合最优控制(multi objective direct hybrid optimal control，MODHOC)工具箱。Pritchett等研究了基于配点法的小推力转移轨道的直接优化方法,并设计了轨道链叠加法来进行初值猜测,将初始轨道和目标轨道中间某些弧段的状态作为连接点,将初始猜测值引导到特定的解。文献[9]介绍了空中客车防务及航天公司基于直接多重打靶法开发的小推力转移轨道优化软件OptElec,在考虑地球阴影区和部分摄动的情况下能够设计从近地轨道(low earth orbit,LEO)或GTO转移至GEO的时间或燃料最优的变轨策略。间接法依赖于庞特里亚金极小值原理,将原最优控制问题转化成多点边值问题,再利用微分方程边值问题的求解方法进一步得到最优解。Mazzini等在考虑摄动和地影的情况下采用平均轨道根数法简化动力学方程,通过打靶法求解了经间接法转化后的两点边值问题,得到了GEO卫星依靠电推力器提升轨道的最优策略。Bastante等研究了基于序列梯度修复算法的GTO-GEO小推力轨道转移间接优化方法,并讨论了如何处理推力方向变化的连续性、最大角速度等约束条件。段传辉等则提出了推力同伦的方法求解两点边值问题,简化了间接法中对于协态变量初值猜测的复杂度,并以GTO-GEO小推力轨道提升问题为例对算法进行了验证,通过5次推力缩减,最终得到了时间最优的转移策略。文献[12-14]中则采用了反馈控制法,设计了基于李雅普诺夫函数的近端商制导律(proximity quotient guidance law,Q-law),作为小推力轨道转移的控制策略。其中,文献[12]和文献[13]中对GTO-GEO的小推力转移过程进行了仿真,表明了该方法能够实现时间次优的轨道转移闭环控制。

上述研究中所述的方法虽然均能够得到优化的小推力变轨策略,但是在复杂度、灵活性、最优性等方面却各有优劣,直接法的变量规模巨大,计算复杂;间接法中协态变量初值猜测较为困难;反馈控制法则无法保证策略的最优性。近年来有越来越多的研究者都采用强化学习方法来解决控制与决策问题,Bertsekas更是全面研究和阐述了强化学习与最优控制的理论联系,同时也有研究者采用强化学习方法解决行星际轨道优化问题。可以得知，采用强化学习方法解决复杂的最优控制问题在简易性、灵活性和最优性方面均具有比较出色的表现,能够处理较为复杂的约束。因此,本文采用了强化学习的方法,求解小推力变轨最优策略,在考虑摄动、地影等多种复杂约束的情况下,训练智能体的神经网络,得到轨道转移决策模型。

本文的主要贡献如下:①在演员-评论家(Actor-Critic)强化学习框架下建立连续小推力变轨决策模型,结合广义优势估计和近端策略优化方法训练深度神经网络,以其为非线性逼近器,探索小推力轨道转移的最优推力方向变化策略;②以轨道摄动方程、空间环境摄动、地球阴影区约束的数学模型为基础,建立可与智能体交互的环境模型;③针对由于状态空间过大而导致智能体探索困难的问题,提出了动作网络输出映射和分层奖励的方法,缩小了探索空间,显著地提高了智能体探索到目标轨道的效率,有效缩短了训练时间。最后,通过几组不同初始参数的结果对比,验证了求解得到的变轨策略的最优性。

1 问题描述

1.1 预备知识

连续小推力轨道转移问题中,作用于卫星的推力加速度量级一般为10～10km/s,稍大于作用于卫星的空间摄动力的大小。因此,若采用经典轨道六根数来描述卫星的轨道,那么卫星的轨道动力学模型应采用高斯型拉格朗日行星摄动力方程表示:

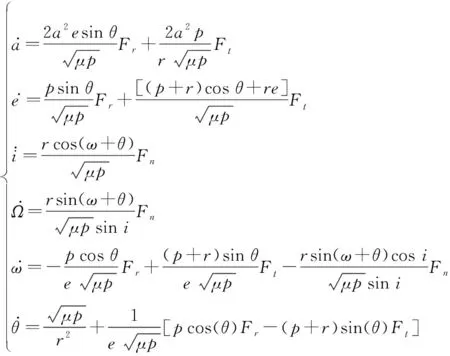
(1)

式中:

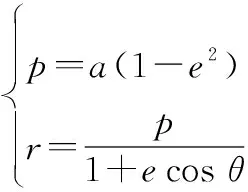
(2)

为半长轴;为偏心率;为轨道倾角;为升交点赤经;为近地点幅角;为真近点角;为轨道半通径;为卫星质心到地心的距离;为地球引力常数;、、分别为作用于卫星的合力在卫星轨道坐标系3个坐标轴方向产生的加速度,分别对应径向、轨道面内垂直于径向、轨道面法向3个方向。

本文采用强化学习的方法求解小推力变轨问题。强化学习方法通过智能体与环境的交互过程获得回报,如图1所示,从而更新智能体的策略,在实现特定目标的同时使回报最大化,进而得到最优策略。

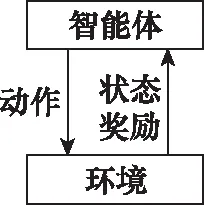
图1 智能体与环境交互图Fig.1 Interaction between agent and environment

在智能体与环境的交互中,智能体需要多次重复从初始状态到目标状态的过程以获得训练数据,重复一次称为一回合,而一回合中又包含很多步,用和分别表示智能体在第步的状态和动作,此过程将产生一组状态-动作序列(,,…,,),其中(,)表示智能体探索到特定目标前的最后一对状态-动作,状态与动作既可以是标量,也可以是矢量,需要根据实际问题定义。该状态-动作序列即代表了智能体在一回合中的轨迹,用表示。可以定义第步的累积回报函数为

(3)

式中:()表示轨迹的回报;(,)表示在状态下采取动作的单步回报。在基于策略的强化学习方法中,目标函数可以表示为

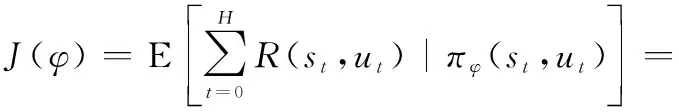
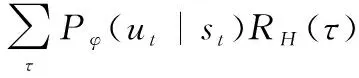
(4)

式中：变量泛指智能体从状态到动作的映射中涉及到的参数,参数不同即代表不同的策略；E(·)表示期望；表示在参数下的策略；(|)表示在参数下的策略在条件下执行的概率。强化学习的最终目标则是找到最优的参数,使得目标函数达到最大值,用公式描述为

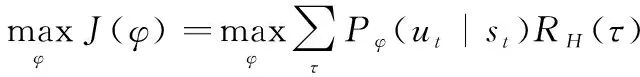
(5)

实际上,强化学习问题变成了一个优化问题,采用文献[27]提出的策略梯度优化方法,即

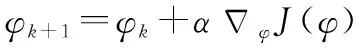
(6)

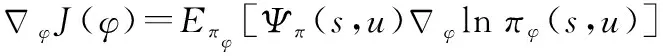
(7)

式中：(,)为评价函数。在Actor-Critic框架下,(,)为Actor,(,)则为Critic,二者均采用神经网络来表示,分别称为动作网络和评价网络。Actor的实际输出值为归一化的值,一般取值范围为[-1,1],在与环境交互前需进行变换,映射到相应的动作空间中。Critic的输出值为当前状态及动作的价值。

1.2 问题建模

本文研究全电推进卫星转移至GEO的时间最短变轨策略,卫星的动力学模型采用式(1)中的微分方程描述,式中的加速度项可以拆分为电推力器提供的加速度和摄动加速度两项,即

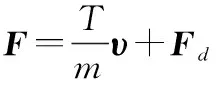
(8)

式中：为在卫星轨道坐标系中卫星的合加速度矢量,=(,,)；为电推力器产生的合力大小；为当前时刻的质量；为推力在卫星轨道坐标系下的单位矢量;则为卫星所受的摄动加速度,包括地球非球形引力摄动、日月引力摄动、太阳光压摄动、大气阻力摄动等。

在变轨过程中,卫星质量随着工质的消耗而减小,变化率为

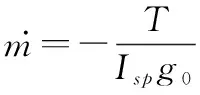
(9)

式中：为电推力器的比冲；为重力加速度。

假设表示推力单位矢量在轨道面内的投影与径向的夹角,表示推力单位矢量与轨道面的夹角,则可以写为

=(coscos,sincos,sin)

(10)

卫星的推力指向即可用和两个参数表示,若不考虑工程上的推力指向范围约束,可取∈[-90°,270°],∈[-90°,90°]。因此,全电推进卫星的变轨策略优化也就是对、两参数的变化策略进行优化。因此,问题可转化为如下优化指标:

(11)

令=(,,,,,),则系统的状态方程可以写为

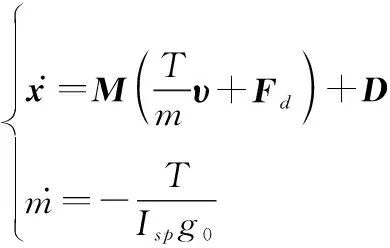
(12)

式中：为6×3矩阵,为6×1矩阵,具体表达式见文献[28],=(,)∈为状态空间,=(,)∈为动作空间,优化目标为时间最短,任务目标轨道为GEO。

2 轨道优化方法

2.1 环境模型

强化学习算法要求建立可供与智能体交互产生数据的环境模型,即图1中的环境模块,其输入是智能体的动作,输出为采取动作后达到的状态以及当前动作的奖励。由于目标轨道是GEO,其倾角为零且为圆轨道。当达到目标轨道时,轨道的升交点赤经和近地点幅角产生了奇异。为了避免这种奇异,本文采用改进的春分点轨道根数(,,,,,)描述强化学习过程中的状态,与经典轨道六根数转换关系如下:

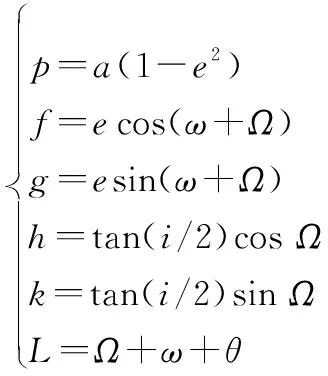
(13)

相应的状态转移方程为

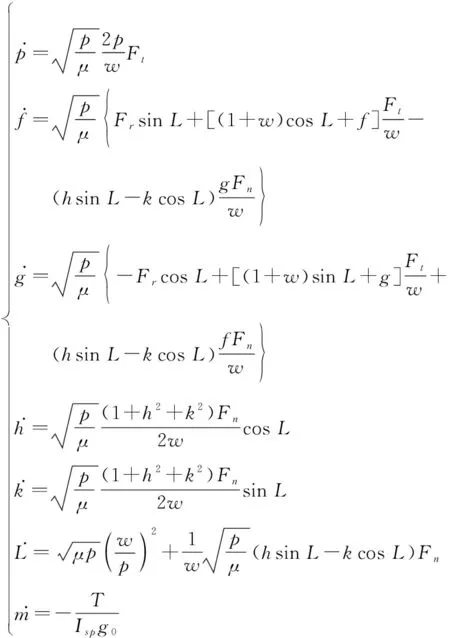
(14)

式中:为辅助量,定义如下:

=1+cos+sin

(15)

本文仅在智能体训练中采用式(14)替代式(12)作为与智能体交互的状态转移模型,在分析问题时仍采用式(1)。

为更加贴近真实情况,使得到的策略更具工程意义,需要考虑摄动和地影的影响。考虑的摄动包括地球非球形引力摄动、日月引力摄动、太阳光压摄动、大气阻力摄动等,其数学模型对应文献中一致,这里不过多赘述。将得到的各种摄动加速度经过坐标变换并求和,可得到卫星轨道坐标系下的摄动加速度,代入式(8)中,即可得到卫星在空间中的合加速度。

此外,地球阴影区对全电推进卫星变轨的影响也需要考虑在内。由于电推力器主要靠太阳能转化成的电能驱动,因此当进入地影区时,太阳帆板被遮挡,卫星须关闭电推力器滑行。本文采用圆锥形地影模型,通过太阳矢量和卫星位置矢量计算出地球-卫星-太阳夹角、卫星上观察太阳的视半径以及卫星上观察地球的视半径。通过三者关系即可得知卫星的地影情况,用可视因子表示太阳被地球遮挡的程度,有以下关系:

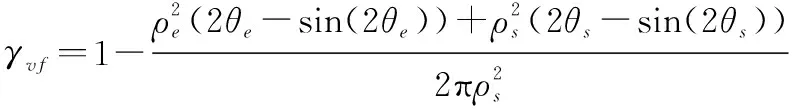
(16)

取值范围为[0,1]。其中,与为中间变量:

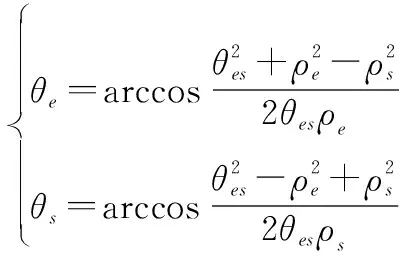
(17)

如图2所示,当=1时,卫星位于阳照区,地球对太阳无遮挡;当=0时,卫星位于本影区,地球完全遮挡太阳;当0<<1时,卫星位于半影区,地球对太阳的遮挡程度随着的值减小而增加。

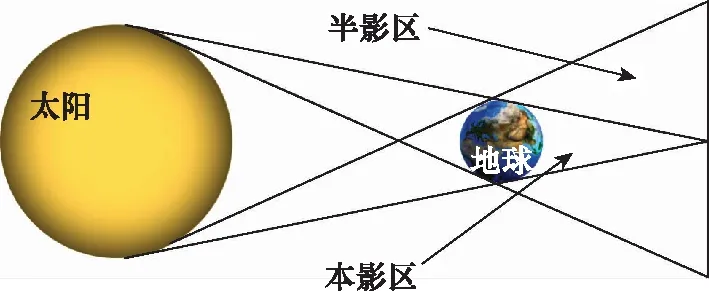
图2 圆锥形地影模型示意图Fig.2 Schematic diagram of conical earth shadow model

卫星位于半影区内太阳可视因子较大的区域时,电推力器也能够点火。本文假设>01时,电推力器可点火,当≤01时，电推力器关机,卫星滑行。

2.2 改进的近端策略优化方法

本文采用结合广义优势估计(generalized advantage estimator, GAE)的近端策略优化(proximal policy optimization, PPO)(GAE&PPO)方法对所提出的问题进行求解。PPO属于强化学习方法的一种,基于Actor-Critic框架而提出,其核心优化公式如下:

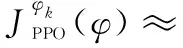
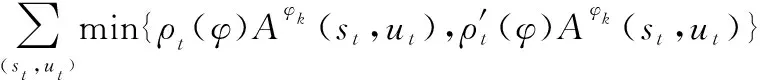
(18)

其中,

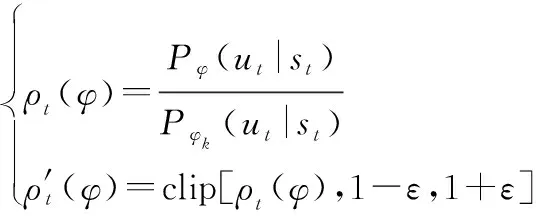
(19)

式中:()为概率比,表示新老策略的差异;clip(·)为剪切函数,用来将()限制在[1-,1+]之间,如果超过边界值则取边界值;为剪切率,限制()的剪切范围,代表了更新策略的探索性,越大,算法越容易探索到新的状态,但影响稳定性。优势函数定义为

(,)=(,)-()

(20)

(,)表示当前步状态-动作值函数(,)与状态值函数()之差,由评价网络产生,用来评价在步时采取动作的优劣,为值函数的相关参数。

值函数的参数属于评价网络中的参数,其更新方法同样采用策略梯度法：

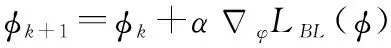
(21)

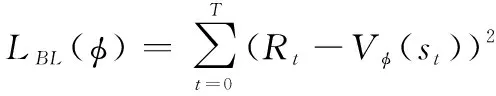
(22)

式中:()为值函数的目标函数;为第步的累积奖励值。

在评价网络估计优势函数时,常常用逼近算法近似计算值函数,因此会引入偏差,文献[37]中提出了广义优势函数估计:

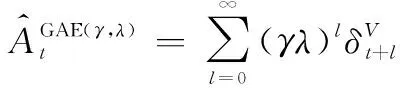
(23)

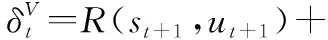
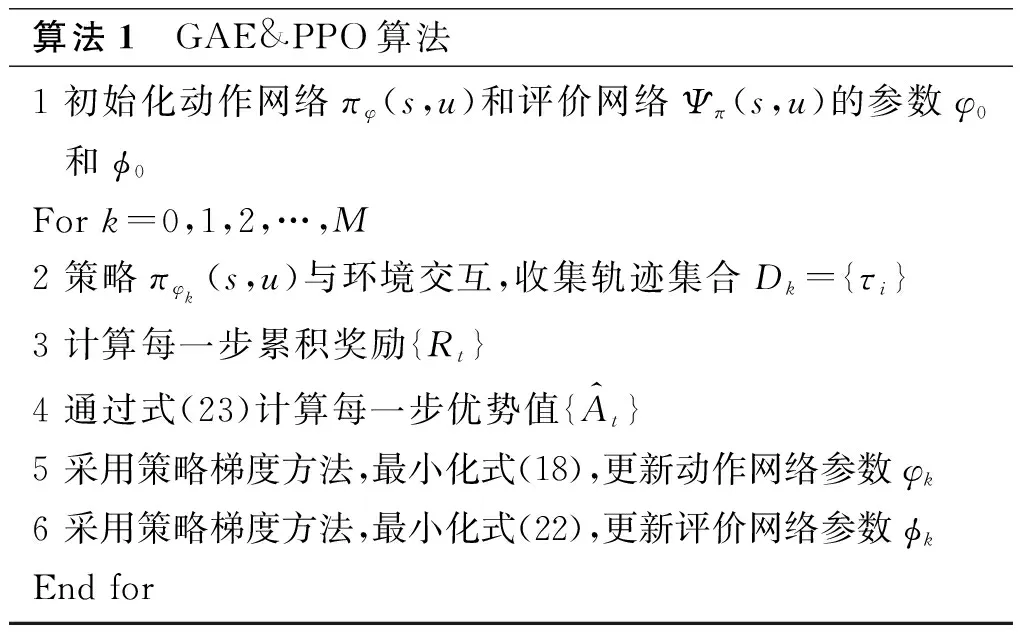
GAE&PPO算法流程如下。

算法1 GAE&PPO算法1 初始化动作网络πφ(s,u)和评价网络Ψπ(s,u)的参数φ0和ϕ0For k=0,1,2,…,M2 策略πφk(s,u)与环境交互,收集轨迹集合Dk={τi}3 计算每一步累积奖励{Rt}4 通过式(23)计算每一步优势值{A^t}5 采用策略梯度方法,最小化式(18),更新动作网络参数φk6 采用策略梯度方法,最小化式(22),更新评价网络参数ϕkEnd for

由于采用了概率分布和采样的方式确定下一步动作,因此GAE&PPO算法的稳定性和收敛性更好,算法具体流程如图3所示。

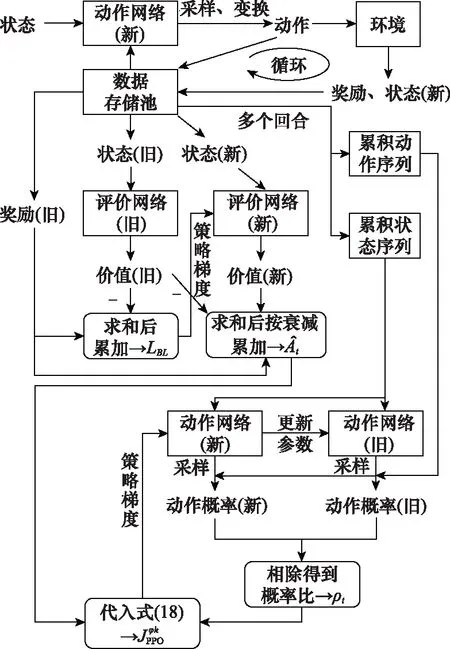
图3 GAE&PPO算法流程图Fig.3 GAE&PPO algorithm flow diagram

3 训练加速方法

本文中智能体要在七维状态空间中探索到目标状态,寻找这一过程中时间最优推力指向序列,而目标状态仅为GEO附近能够进行轨道捕获的小范围区域。智能体在状态空间中很难探索到目标状态,导致有效训练数据不足,训练过程十分缓慢甚至难以完成训练,这是强化学习方法解决小推力变轨问题的难点之一。本文提出了以下方法解决这一难点。

3.1 动作输出映射

轨道转移的目标状态限制了半长轴、偏心率和轨道倾角3个参数,卫星从初始轨道到目标轨道需要完成提高半长轴、减小偏心率、压低轨道倾角3方面内容。本文通过分析轨道动力学方程,提炼出能够实现这3方面内容的推力指向角、的粗略变化规律。根据提炼出来的先验知识,对动作网络的输出进一步设计,使半长轴、偏心率和轨道倾角3个参数始终向目标值靠近,从而缩小探索空间。

由前文可知,动作网络的实际输出值需要做线性变换才能与环境交互,因此可以在这一过程中引入先验知识。

暂时忽略式(8)中摄动加速度的影响,将式(10)代入式(8),得到推力加速度矢量三维分量关于的表达式

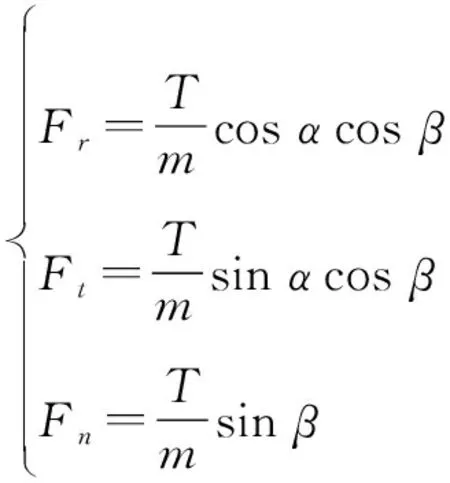
(24)

将式(24)代入式(1)中的半长轴、偏心率和轨道倾角微分方程,整理得到:

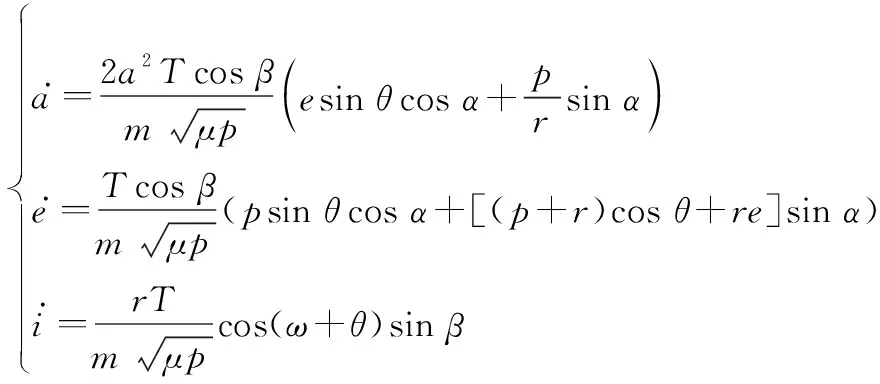
(25)

若使、、尽可能向目标值靠近,须满足以下条件:

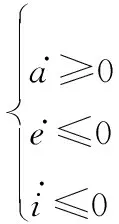
(26)

由于,∈[-90°,90°],cos≥0,因此,将式(25)代入式(26)可以得到

(27)

由式(27)可知,半长轴、偏心率的增减与∈[0°,180°]有关,轨道倾角的增减与∈[0°,180°]有关,因此可以通过式(27)得到:

(1)当∈[0°,180°]时,若使半长轴增大,则∈[0°,90°];若使偏心率减小,则∈[-90°,-]∪[180°-,360°-]。

(2)当∈(180°,360°]时,若使半长轴增大,则∈[90°,180°];若使偏心率减小,则∈[180°-,360°-]∪[540°-,270°]。

(3)当+∈[0°,90°]∪(270°,360°]时,若使轨道倾角减小,则∈[-90°,0°]。

(4)当+∈(90°,270°]时,若使轨道倾角减小,则∈[0°,90°]。

对轨道摄动情况进行分析,可以得知在变轨前期轨道高度较低的弧段,地球非球形引力摄动和大气阻力产生的摄动加速度相对较大,因此变轨前期主要提升半长轴。

综合以上分析可以得知,能够实现轨道转移任务的策略具有以下几个特点:① 变轨前期主要增大半长轴,推力在轨道面内分量主要分布在速度方向附近;② 变轨后期进一步提升半长轴,同时减小偏心率,推力在轨道面内分量随真近点角程周期变化;③ 整个变轨过程中推力矢量在轨道面法向的分量在升交点侧的一半弧段指向负法向,在降交点侧的一半弧段指向正法向。

假设动作网络的实际输出为(′,′),根据上述特点对其做以下变换:

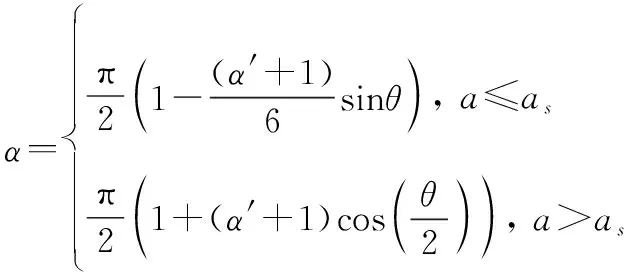
(28)

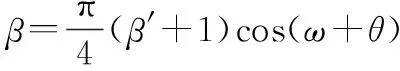
(29)

式(28)和式(29)在最优策略的必要条件下对、进行粗略约束,不影响策略最优性的同时使卫星更容易探索到目标轨道,从而获得更多的有效训练数据。其中,变轨阶段临界点的最优值在强化学习训练循环中采用随机搜索的方法求解。

3.2 分层奖励设计

在强化学习中,奖励通过环境传递给智能体,智能体的训练目标是使总收益最大化,因此奖励函数的设计尤为重要。

当前的优化目标是时间最优,一般的时间最优奖励函数形式为

(30)

式中：为一个较小值,代表耗时惩罚;为一个较大值,代表完成任务目标的奖励。

上述奖励函数虽然能够保证优化目标的实现,但是训练过程中可能达不到任务目标,导致很多无效的训练。因此,根据本文实际问题,设计奖励函数如下：

(31)

式中：、、和、、分别为当前时间步和目标的半长轴、偏心率和轨道倾角。其他情况中包括耗时惩罚和偏离任务目标惩罚。

前文中奖励函数虽然引入了偏离任务目标的惩罚项,但是智能体中神经网络由于采用了随机初始化参数,训练效率受神经网络初始化影响较大,在训练初期仅通过的奖励值首次探索到目标轨道的用时不稳定。因此,在的基础上,设计了更加有利于探索到目标的奖励函数:

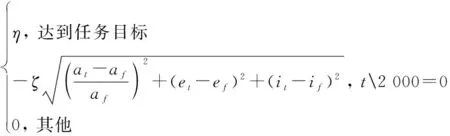
(32)

式中：为取余符号。中每隔2 000个时间步计算一次当前状态与目标的偏差,其余情况奖励为0,取消对时间的寻优,只探索目标状态,提高任务成功率。

结合和的优势,本文设计了分层奖励方法,将训练过程分为两个层次,下层训练采用作为奖励,上层训练采用作为奖励,训练初期从下层训练开始,优先探索能够达到目标状态的策略,当某一回合智能体成功达到目标状态时,则在此基础上开始上层训练,进行时间最短策略寻优。

采用上述方法优化后的智能体与环境交互模型如图4所示。

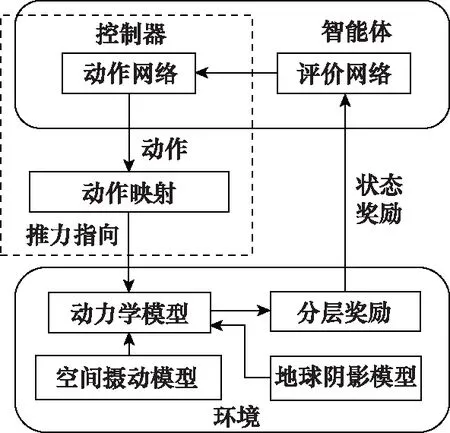
图4 改进的智能体与环境交互模型Fig.4 Improved agent-environment interaction model

4 结果分析及对比

4.1 训练结果

采用前文所提到的强化学习及训练加速方法对全电推进卫星轨道转移问题进行求解,验证方法的可行性和最优性。

假设在协调世界时(universal time coordinated, UTC)下的历元时刻2021年1月1日12:00:00,卫星位于初始轨道,其初始轨道和目标轨道参数如表1所示,卫星初始质量为1 600 kg,携带两台装有矢量调节机构的离子电推力器,可产生推力合力大小为400 m·N,比冲为2 000 s,太阳光压反射率为1,光压等效面积为20 m,在低轨道时的大气阻力系数为2.2,迎风面积为20 m。

表1 卫星轨道根数初始值和目标值

当卫星达到目标轨道附近且半长轴偏差小于0.5 km、偏心率小于0.1、轨道倾角小于0.1°时,即认为当前回合成功达到任务目标。当卫星半长轴大于42 170 km、偏心率大于1、轨道倾角大于90°时,则认为探索超出边界,任务失败。

算法中动作网络和评价网络均采用三隐层平行结构,每层神经元节点数为128个,学习率均设置为10,激活函数采用ReLu和Hardswish两种函数,具体结构如图5所示。

图5 智能体包含的神经网络结构示意图Fig.5 Schematic diagram of neural network contained in agent

训练过程中还涉及到前文中提到的一些其他参数,具体参数值如表2所示。由于算法的稳定性和收敛性较好,因此超参数设置在合理的范围内即可,选取较为容易。

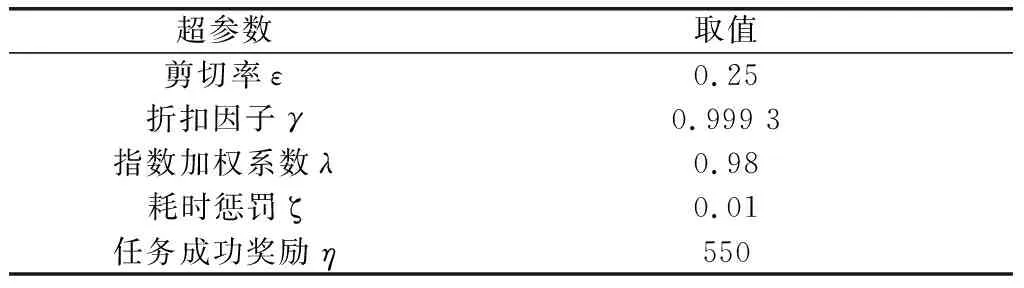
表2 其余参数选取

采用Python语言实现网络结构并训练,用每回合累积奖励的变化来表示训练效果,得到的训练曲线如图6所示。

图6 学习曲线Fig.6 Learning curve

由图6可知,在训练初期,智能体未能探索到目标状态,奖励函数为,此时奖励为状态与目标状态偏差所产生的惩罚项,因此累积奖励为负值。随后,智能体通过最小化偏差探索到任务目标,获得任务目标奖励,因此累计奖励产生了较大的阶跃,同时开始对转移时间优化。在此阶段中,由于策略的探索性,智能体会探索到目标状态之外,因此会产生累计奖励突然下降的情况,由于中同样存在偏差项,智能体能够重新找到目标状态,从而继续优化任务时间,最终累积奖励稳定到一个范围内,从中选取最大累积奖励对应的参数,得到动作网络模型,即可得到时间最优的转移策略。最大累积奖励为176.84,对应的轨道转移时间为142.11 d。

将得到的动作网络与环境交互,即可得到时间最优的推力方向变化序列以及相应的轨道变化序列,其中半长轴、偏心率、轨道倾角变化曲线如图7所示。

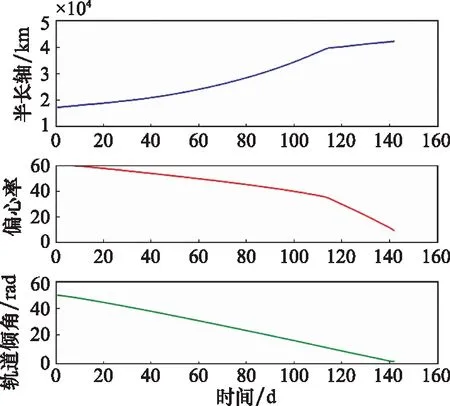
图7 卫星轨道根数变化曲线Fig.7 Orbit elements curve of satellite

卫星变轨轨迹如图8所示,其中蓝色部分为阳照区电推力器点火弧段,红色部分为地影区电推力器关机滑行阶段。

图8 卫星变轨轨迹Fig.8 Trajectory during satellite orbit transfer

4.2 效果对比

在不同的变轨问题以及约束条件下,对比本文方法与其他方法的优化效果,采用不同文献中的初始轨道参数作为初值,如表3所示,分别求解时间最优的轨道转移策略。

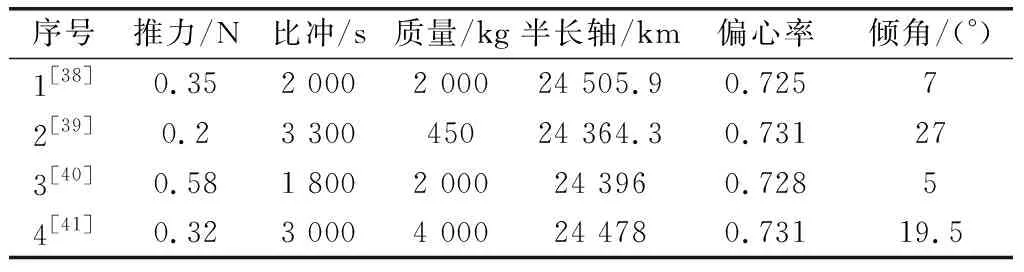
表3 参考文献中的初始轨道参数

表4中列举了采用文献中各自算法求解得出的最优转移时间和采用强化学习方法求解得到的转移时间。其中,情况1是在开普勒模型下的结果,忽略了地影和摄动的影响;情况2和情况3只考虑了地球的J2摄动项以及地影区约束;情况4则是在全引力模型以及地影区影响下的计算结果。

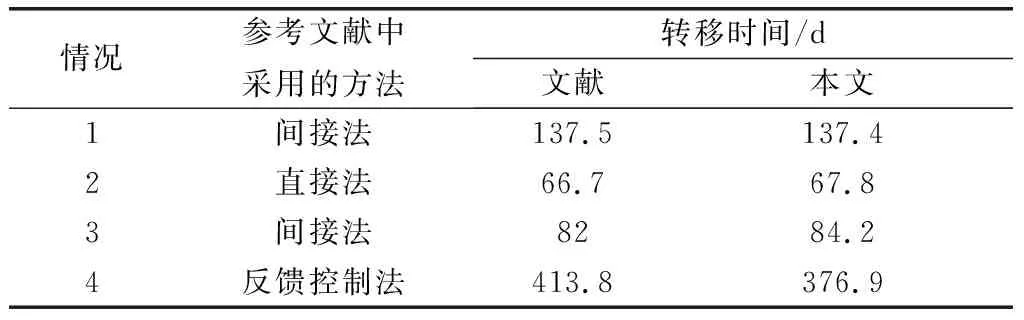
表4 不同情况下的轨道转移时间对比

通过表4中的结果对比,可见在不考虑地影约束和摄动影响的情况下,采用本文所述方法得到的最优轨道转移时间与采用间接法得出的最优结果基本一致。在仅考虑J2项非球形引力摄动和地影区约束的情况下,本文方法得到的最优结果与文献中的最优结果相近,但略差于最优结果,差距控制在3%以内。在考虑全部摄动以及地影区影响的情况下,本文方法与反馈控制法计算得到的最优结果相比有较大的提升。因此,由上述内容可以得出,在不同初始轨道参数、考虑不同环境影响的情况下,所设计的轨道优化算法仍然能够计算出接近最优的轨道转移策略。

在求解效率方面,求解GTO-GEO小推力转移轨道问题需要计算每一轨的推力方向变化策略,共包含了几百甚至上万个变量,求解计算量较大。直接法求解时涉及到的变量和约束多达几十万个,求解时间长达几小时甚至一整天。间接法虽然求解计算量小,但是由于协态变量需要猜测初值,初值猜测不准确将导致求解时间延长甚至无解。本文所提到的方法不需要同间接法一样进行准确的初值猜测。同时,相比于直接法,本文方法涉及到的变量和约束少,求解时间更短,如图6所示,经过3 000个批次的训练即可达到最优解,采用GPU(NVIDIA GeForce RTX 2080Ti)训练,求解时间为两小时左右。

5 结 论

本文研究了将强化学习算法引入小推力轨道优化问题中的具体实现方法。首先采用高斯型轨道动力学方程、各种空间摄动方程以及地影模型对强化学习所需的环境进行了建模,得到了可以参与训练的环境模型。随后,将GAE和PPO方法结合,得到了改进的近端策略优化算法,使算法更加稳定,同时减小了值函数的偏差。针对训练中遇到的由于奖励稀疏而难以收敛的问题,提出了动作输出映射和分层奖励等方法,显著加快了收敛速度。最后,通过数值仿真,证明了算法的有效性。通过与其他文献中采用不同方法计算得到的结果对比,表明了所提算法具有轨道转移时间的最优性。同时,所提方法既不需要对初值进行猜测,也不需要优化大量的变量,相比于其他方法更加简便、灵活。本文对采用强化学习方法解决全电推进卫星轨道优化问题做了初步研究,只考虑了变轨过程中空间环境的约束,并没有考虑工程上的约束,如推力指向调节范围、卫星姿态角速度限制、燃料消耗量、同步轨道定点等约束。因此,研究带有以上工程约束的小推力变轨策略是后续的研究方向之一。