激振力作用下桩侧土液化特性及拔桩过程分析

杨胜文, 石 旷, 杨吉新, 凌中水

(1.中国一冶集团有限公司,湖北 武汉 430080; 2.武汉理工大学 交通学院,湖北 武汉 430063; 3.安庆职业技术学院 机电工程学院,安徽 安庆 246003)

振动锤常用于桩基础的施工中,其原理是利用振动锤内部偏心块转动的离心力,产生竖直方向正弦激振力[1-4]。当桩入土深度较深或土质情况复杂时,用一般的起重设备施加静力进行拔桩施工难度较大,此时通常用振动锤在桩顶施加激振力,充分激振后使得桩侧土软化或液化,桩侧阻力大幅削弱,从而达到顺利拔桩的目的。对于饱和土中振动锤拔桩过程的分析,研究桩侧土的液化特性十分关键。Seed、Ishihara、汪闻韶等提出了土液化相关理论[5-8];文献[9]建立饱和砂土固相颗粒和液相流体耦合的模型,采用计算流体动力学技术分析饱和砂土的液化效应;文献[10]提出一种新的本构模型用于模拟土体液化后的强度及液化后的响应;文献[11]对某盾构隧道处地层在地震作用下的液化效应进行分析;文献[12]提出适用于不同土层的双曲线形式剪切波速判别模型,用于评价土层的液化程度;文献[13]基于振动台试验模拟强震区饱和砂土的液化规律;文献[14]利用动三轴试验研究含气砂土的液化特性。上述对于土液化的研究大多集中于饱和土整体在地震荷载等外部循环荷载作用下的液化效应,针对桩顶振动锤正弦激振下桩侧土体液化效应的相关研究很少。对桩侧土进行液化分析可以评价振动锤的激振效果,对于振动锤拔桩施工具有重要意义。

工程中常要进行拔桩施工[15-18],以达到清障、废桩重复利用等目的。对于静力拔桩过程,已有一些研究成果。文献[19]通过室内模型试验,对砂土中管桩的抗拔特性进行研究;文献[20]对水平与竖向静力上拔组合荷载作用下的桩基承载特性进行试验研究;文献[21]基于离散元对扩底桩的上拔特性进行研究。当桩顶施加激振力进行动力拔桩时,桩与土之间的动力相互作用更为复杂,同时还要考虑桩侧土液化效应的影响,激振力作用下的拔桩过程有待进一步研究。

本文以石首建宁大桥桥下钢管桩为例,通过FLAC3D有限差分软件,利用描述土体液化的Finn模型,首先分析在EP160型振动锤激振力作用下桩侧土的液化效应,得出拔桩施工的可行性,然后分析不同拔桩力作用下桩体的位移时程响应,并通过现场试验实测与数值计算对比,验证FLAC3D计算振动拔桩过程的准确性。

1 土体液化的原理

1.1 本构模型

本文利用Finn模型模拟土受动荷载的液化过程,其基本原理是根据文献[22]提出的公式,即

(1)

C1C2C4=C3

(2)

(3)

(4)

其中:Δεvd为塑性体积应变增量;γ为剪应变;εvd为塑性体积应变;C1、C2、C3、C4为模型常数,可根据土工试验测定,C3为应变阈值,即发生塑性体积应变的最小剪应变值;(N1)60为标准贯入击数。

(1)式很好地描述了土体塑性体积应变增量与不可恢复的塑性体积应变间的函数关系,从细观角度分析,在动力作用下,土体经过一个完整的应变循环,使得土颗粒发生重排并产生不可恢复的体积收缩,在恒定围压下,土体空隙减小,如果空隙中充满流体,那么会导致流体压力增大,从而使土颗粒间的有效应力减小,当有效应力值减小至接近于0时,认为土颗粒已经处于悬浮状态,土体发生液化,因此可通过土体塑性体积应变的变化得到激振过程中孔隙水压力的变化,从而对液化的情况进行判定。

Finn模型是将(1)式与Mohr-Coulomb本构模型整合在一起的新的本构模型,该模型保留了Mohr-Coulomb模型所描述的土材料的非线性及弹塑性,同时能够对土液化过程进行分析。

1.2 土体液化判定方法

当饱和土体在动力作用下有效应力值接近0时,可认为产生液化[23]。假设σ1′、σ2′、σ3′为激振结束后土体的三向有效应力,σ10′、σ20′、σ30′分别为最初土体的三向有效应力,土的有效球应力为p,广义剪应力为q,当有效应力值减小为0时,土体内部应力状态可表示为:

σ1′=σ2′=σ3′=0

(5)

(6)

(7)

为了更加形象描述土体液化过程,利用FLAC3D自带编程语言fish将超孔隙水压比Ru的表达式以额外变量的方式编入程序。Ru的计算公式为:

(8)

(8)式中分母项的初始有效应力随深度变化,当分子项的有效应力值接近于0时,即当Ru值接近于1时表示土体基本液化。

2 工程概况与拔桩数值分析模型建立

2.1 工程概况

石首市建宁大桥全长548 m,主桥为单跨158 m下承式钢-混叠合梁简支系杆钢拱桥。主桥钢梁采用拼装支架施工,施工过程中使用了大量钢管桩作为临时支撑,大桥建成后钢管桩需要拔除回收。桥址范围内总体地形平坦,无滑坡、崩塌、泥石流等不良地质现象,桥梁沿东西向跨越山底湖,湖水深1.6～2.7 m,桥址区岩土体是以粉质黏土、砂性土、黏土及基岩组成的多层结构土体,其中粉质黏土厚0.8～48.8 m,砂性土厚2.3～21.3 m,黏土厚3.3～10.5 m,临时钢管桩架设区域土层主要为粉质黏土。主桥钢管桩布置如图1所示。钢管桩材质为Q235钢,直径为630 mm,壁厚为8 mm。利用浮船设备配合EP160型振动锤,现场进行拔桩试验,试验设备如图2所示。

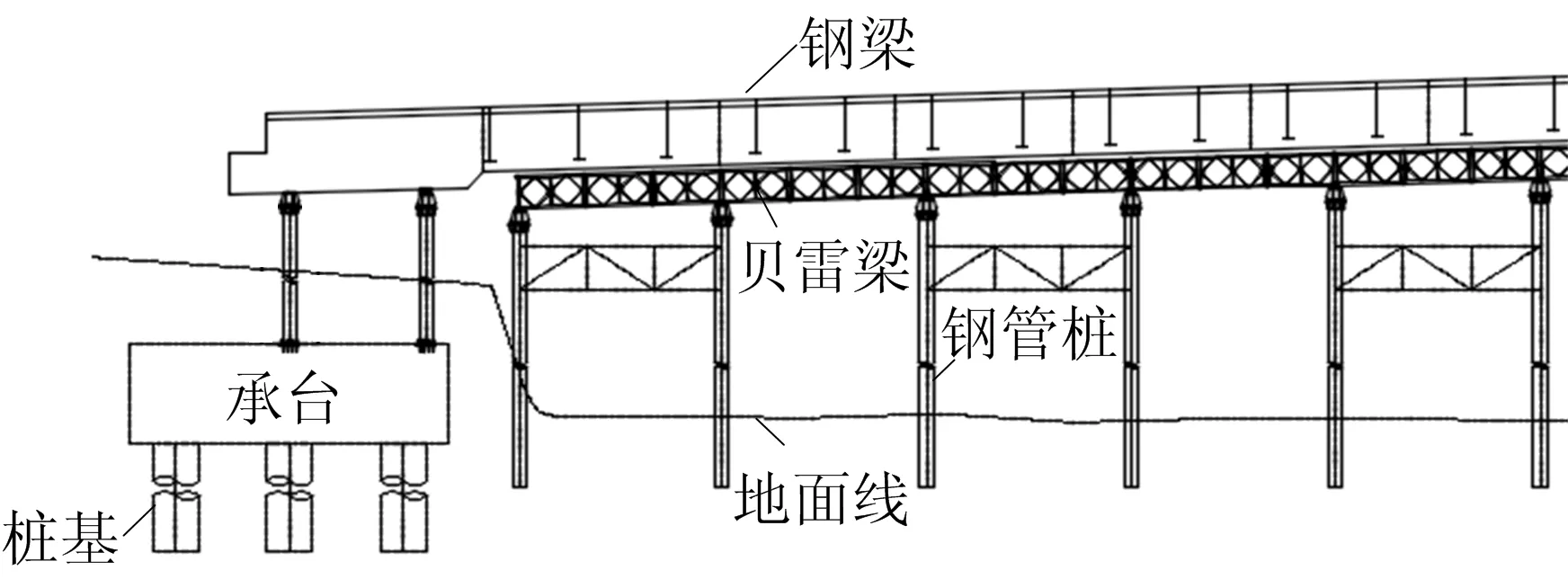
图1 主桥钢管桩支架布置

图2 浮船拔桩设备

浮船拔桩设备由大型浮箱拼装成船体,浮船上受力结构由钢管立柱及贝雷梁组成,振动锤通过滑轮装置,在贝雷梁上可自由调整位置,方便对准钢管桩,拔桩过程中由卷扬机提供上拔力,振动锤提供激振力,试验过程中测量不同桩顶力下钢管桩的位移情况,可反映振动锤的激振效果。

2.2 拔桩数值分析模型建立

利用FLAC3D建立振动锤拔桩模型如图3所示。考虑到缩短计算时间以及远处土体基本不参与受力,土体长度及宽度取30倍桩径,深度取1.5倍桩长,桩-土界面采用面-面接触的方式,在钢管桩外侧及桩侧土表面均设interface接触单元,采用非线性动力分析模块,土体四周建立自由边界减少波在边界上的反射对动力计算的影响,整体模型设置局部阻尼模拟激振过程中能量的耗散。以静力及激振力组合的方式来模拟激振时桩顶荷载,其具体表达式为:

Fd=Fs+F

(9)

其中:Fs为静力;F为振动锤激振力。激振力振幅及频率分别为200 kN、40 Hz,其波形图为按时间变化的正弦函数,激振力示意图如图4所示。

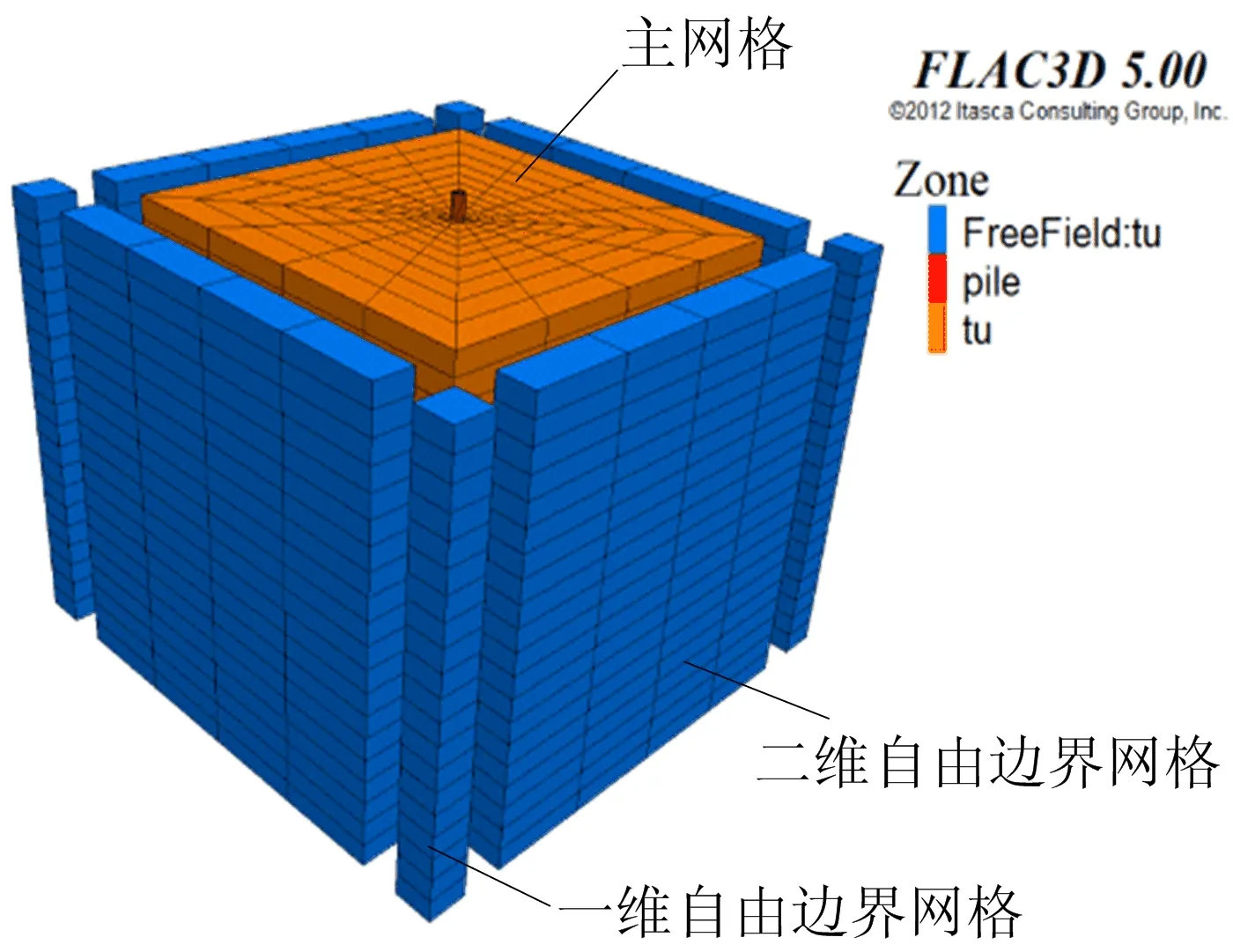
图3 振动锤拔桩数值分析模型

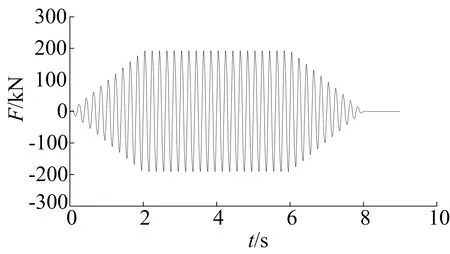
图4 桩顶正弦激振力时程曲线

钢管桩材质按Q235钢设置相关材料参数;桩侧土为单层粉质黏土;由于饱和土动力分析中要考虑孔隙水的影响,动力分析的同时打开流体分析模式。数值分析所需标贯击数由室外原位钻孔标准贯入试验测得,所需渗透系数、孔隙率、干密度、摩擦角、土弹性模量、泊松比由室内土工试验测得。室外钻孔土样及室内试验标准土样如图5所示。

图5 试验土样

所有土样品的试验均按文献[24]执行,所测具体参数见表1所列。

表1 桩侧土物理、力学性能参数取值

3 土体液化及拔桩过程分析

3.1 测点超孔隙水压比分析

考虑到对称性,在桩的一侧布置监测点,监测振动锤激振过程中各测点超孔隙水压比的变化规律。沿深度方向及桩径方向设置5个监测点,各监测点布置如图6所示。

各监测点超孔隙水压比时程曲线如图7、图8所示。从图7、图8可以看出，随着激振时间增加,各点超孔隙水压比迅速增大,说明激振过程中孔隙水压力在不断增大,导致土体单元有效应力不断减小。离振源较近的A、B、D点在激振一段时间后超孔隙水压比接近于1并保持稳定,说明其有效应力已经接近于0,此时可认为A、B、D点的土体单元已达到液化条件。

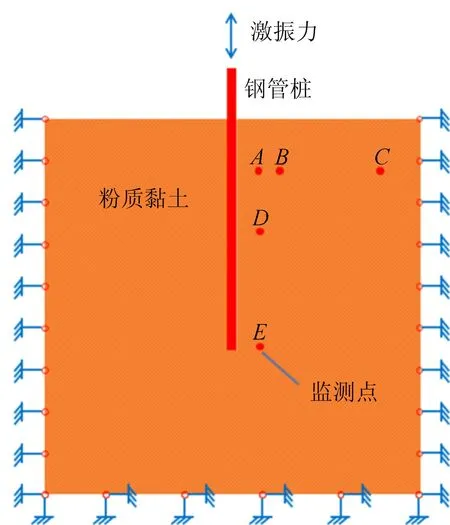
图6 桩侧监测点布置

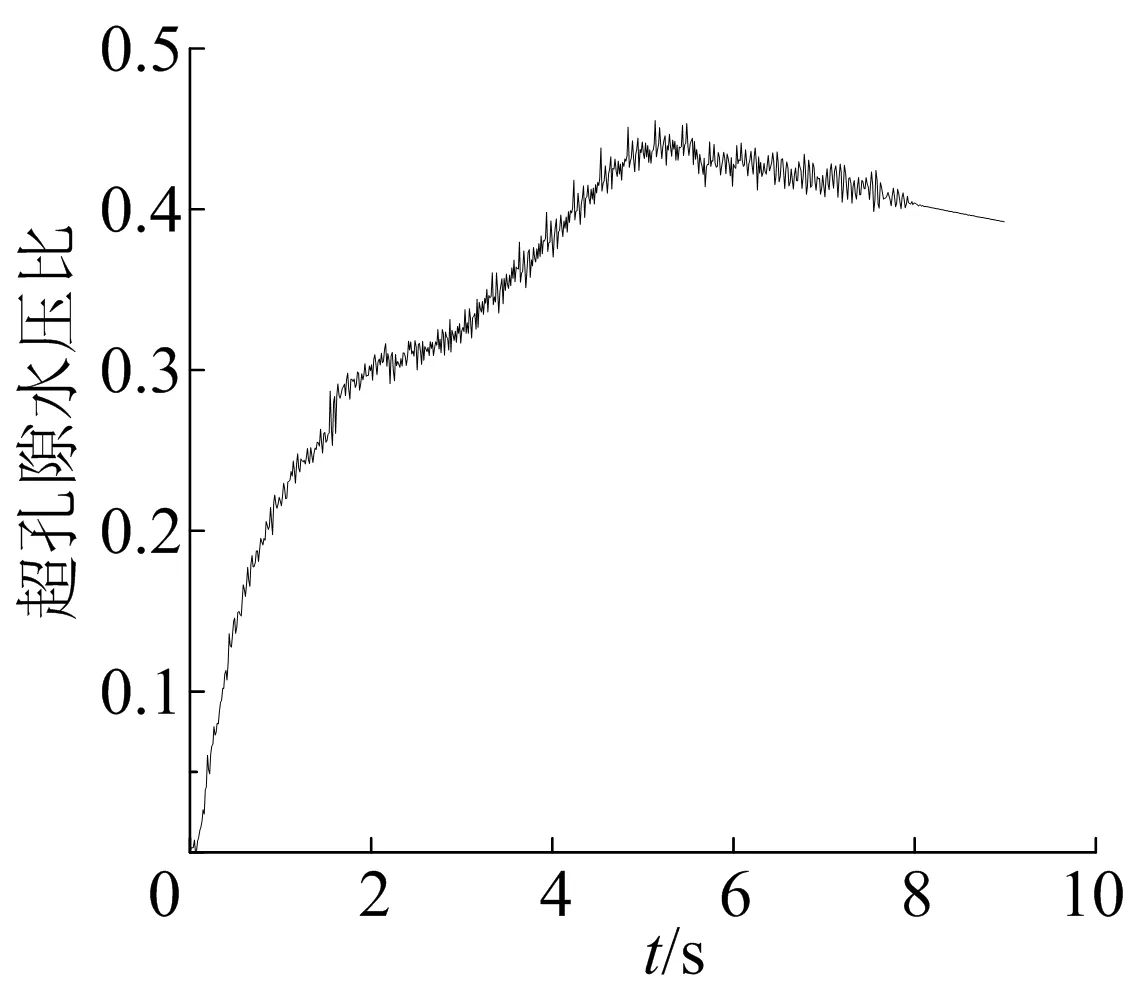
图7 C点超孔隙水压比时程曲线

图8 A、B、D、E点超孔隙水压比时程曲线

而C、E点超孔隙水压比最大值分别为0.43、0.86,并在达到峰值后不断下降,由此可知C、E点的土体未达到液化条件。在动力激振结束后,各测点超孔隙水压比均在减小,说明超孔隙水压力在逐渐消散,桩侧土有重新固结的趋势,由此可知在实际拔桩施工中,激振结束后应尽快进行拔桩施工,避免土体重固结导致抗拔力的回升。

3.2 测点加速度响应分析

为进一步探究桩侧土的液化规律,提取5个监测点的加速度响应曲线,如图9所示。从图9可以看出,各监测点加速度响应波形与桩顶所施加激振力波形相似,即中间振幅较大而两边较小,说明激振力通过桩-土接触面传递到桩侧土,也进一步反映了计算模型的准确性。A、B、D点振幅相对较大,而C、E点振幅较小,从饱和土体中波传递的角度进行分析,桩顶激振力的作用使得桩侧土产生交变的剪切应力,激发出沿径向传递的横波及竖直方向的纵波。因为土体阻尼作用,波传递至离振源较远的C、E点时削弱较大,导致C、E点塑性体积应变的累积较缓慢,所以C、E点在激振过程中并未产生液化,这与前述超孔隙水压比的分析结果相符。

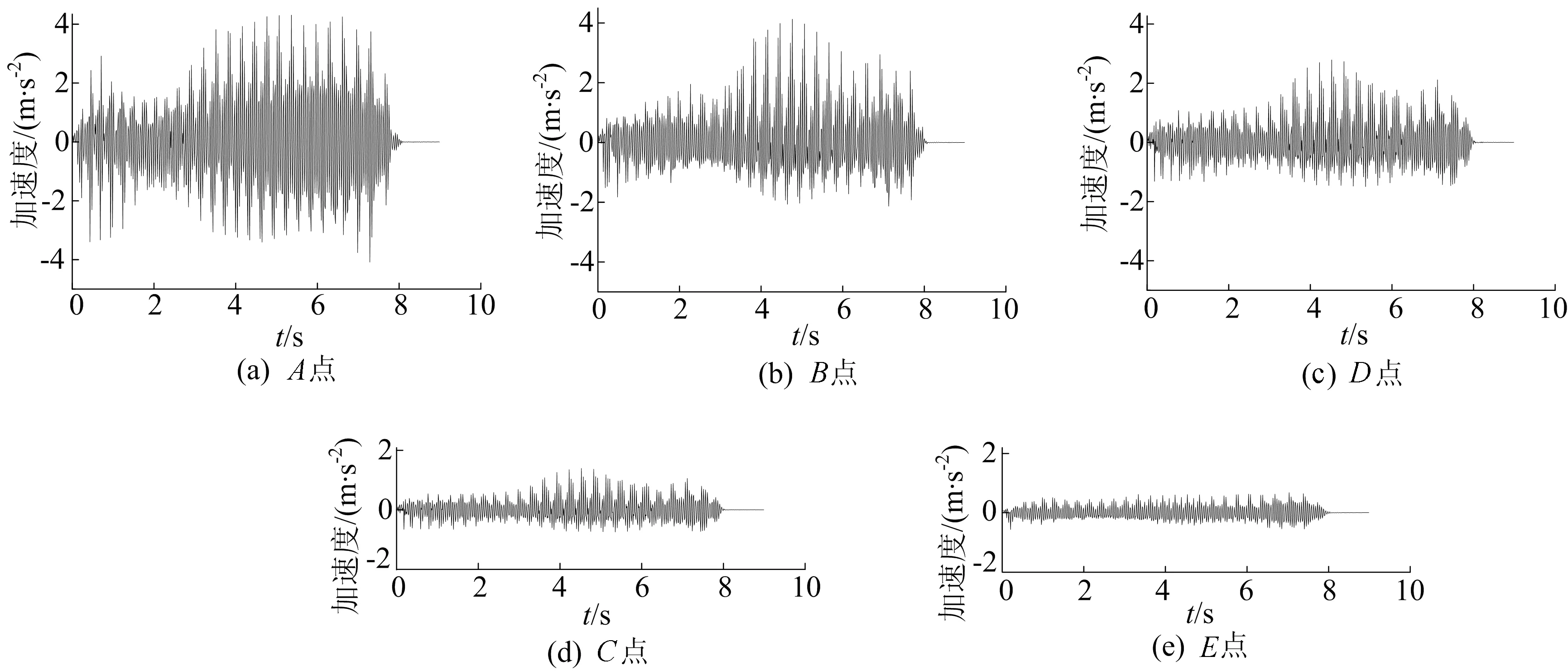
图9 A、B、C、D、E 5个测点加速度响应时程曲线

通过FLAC3D内置编程语言,得到激振结束后桩侧超孔隙水压比云图如图10所示。超孔隙水压比接近1时认为土体具备液化的条件,因此超孔隙水压比云图可表示液化区域,直观反映桩侧土的液化情况。由图10可知,激振结束后桩侧土出现液化区,液化区范围从上到下变窄,表层土受激振力的影响容易产生较大范围液化,中间土层也有一定范围的液化,到接近桩端处桩侧土不再液化。由此综合判断,激振结束后桩侧基本被液化土覆盖,此时桩侧土的抗剪强度值接近于0,拔桩的阻力将大大减小,表明EP160型振动锤激振效果较好,因此可以利用此型号振动锤进行拔桩施工。

图10 桩侧土超孔隙水压力云图

3.3 桩侧摩阻力与拔桩过程分析

在原模型基础上,保持振幅200 kN不变,提取频率分别为0、10、20、30、40、50、60 Hz桩-土接触面切向应力,得到桩侧摩阻力沿深度分布曲线如图11所示。

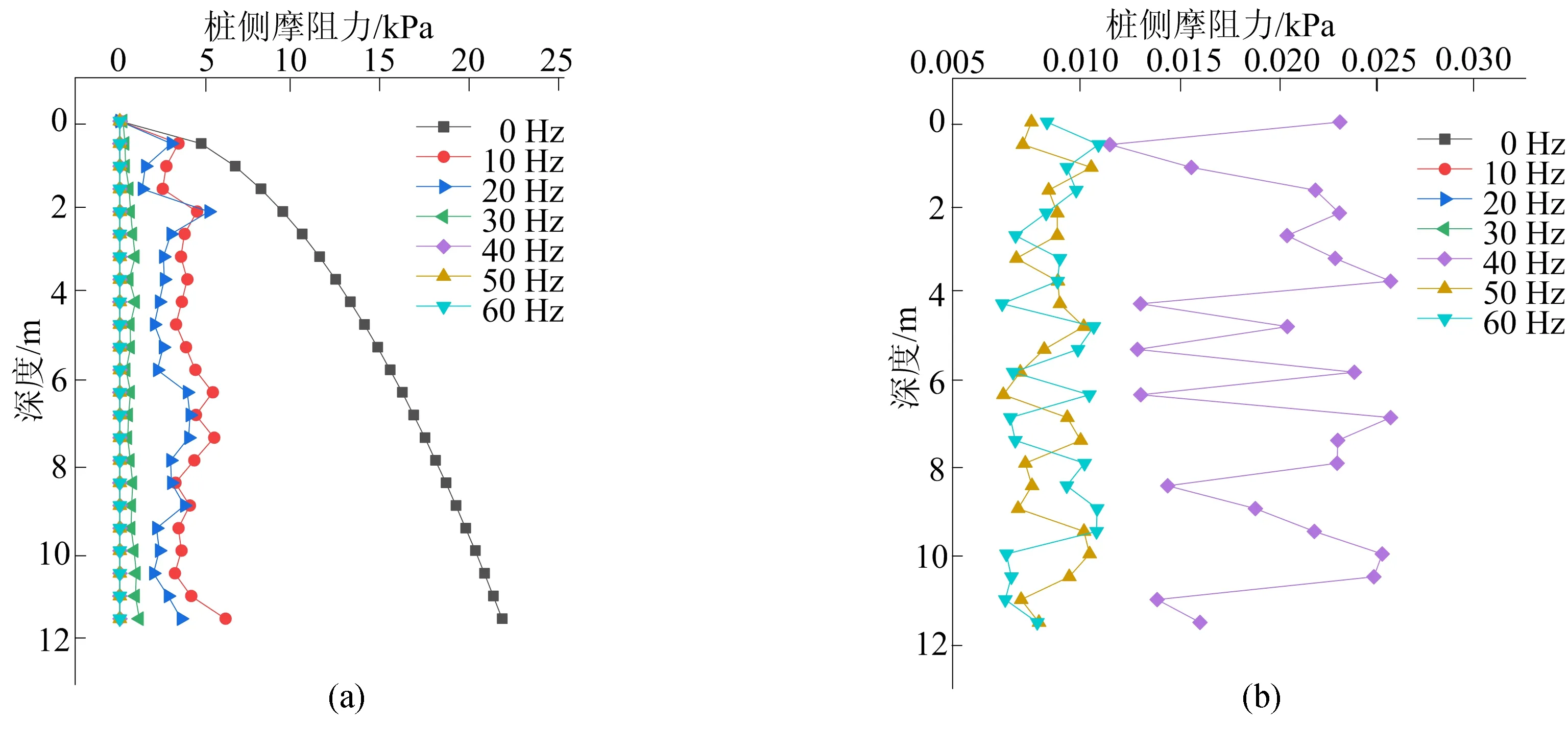
图11 不同激振频率下桩侧摩阻力变化曲线

保持频率40 Hz不变,提取振幅分别为0、100、200、300、400、500、600 kN桩-土接触面切向应力,得到桩侧摩阻力沿深度分布曲线如图12所示。

当频率或振幅值为0时,即桩顶无激振力时,桩侧摩阻力沿深度逐渐增大。增大振动频率到10、20、30 Hz时,侧摩阻力明显减小,此时由于激振力作用,侧摩阻力的分布没有明显规律,40、50、60 Hz时的侧摩阻力值已经接近于0,说明在较高频时桩侧摩阻力削减程度更大;增大振幅到100 kN,侧摩阻力明显减小,振幅在200～600 kN时,桩侧摩阻力值基本为0,反映出增大振幅可以显著降低桩侧摩阻力。振动锤振幅及频率分别为200 kN、40 Hz时,桩侧摩阻力接近于0,这与前述测点超孔隙水压比及加速度分析得出桩侧土液化的结论吻合,说明EP160型振动锤作用下桩侧土大范围液化的同时,桩侧摩阻力也基本消除,从而能提高拔桩效率。

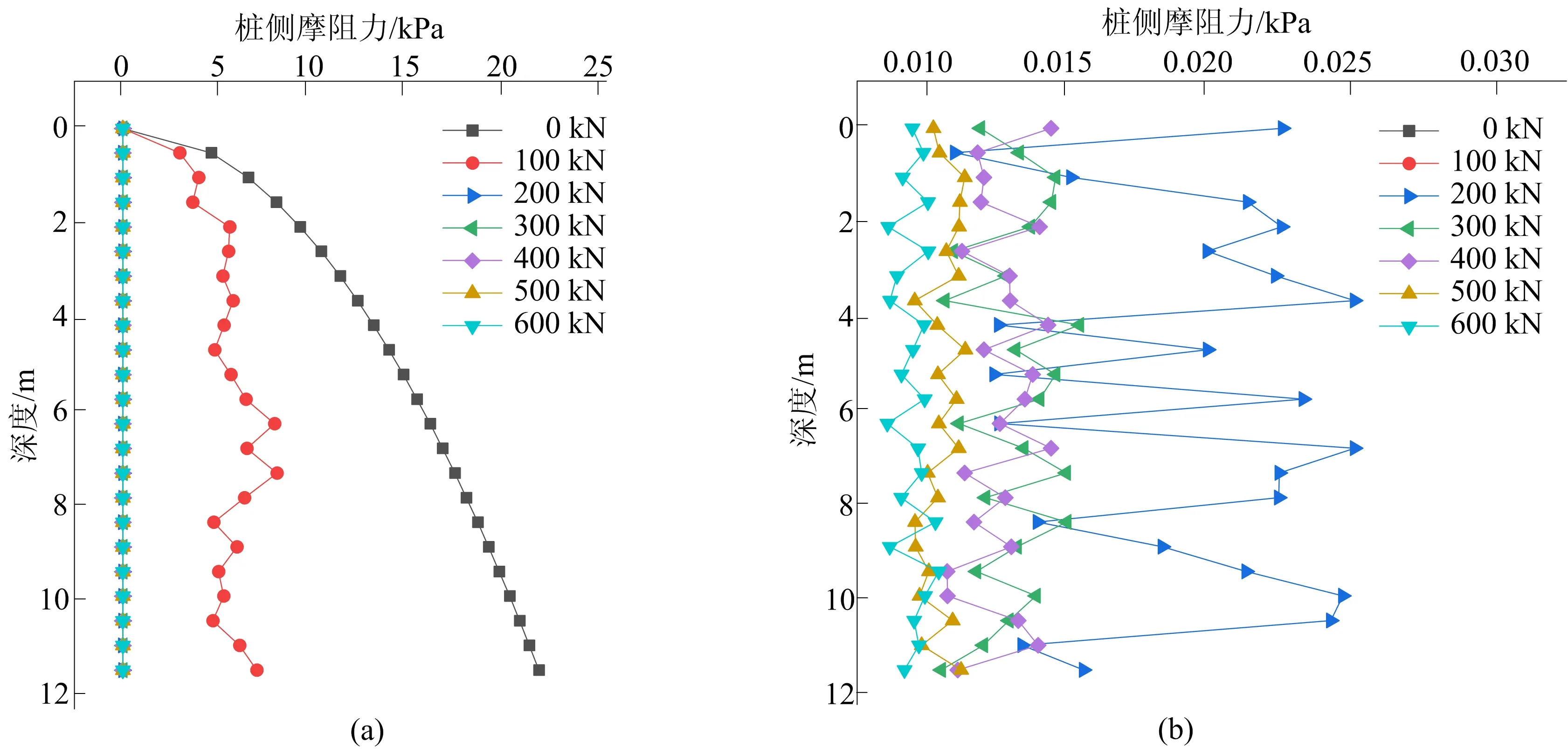
图12 不同激振力振幅下桩侧摩阻力变化曲线

桩顶在100、200、300、400 kN上拔力下钢管桩的位移时程曲线如图13所示。

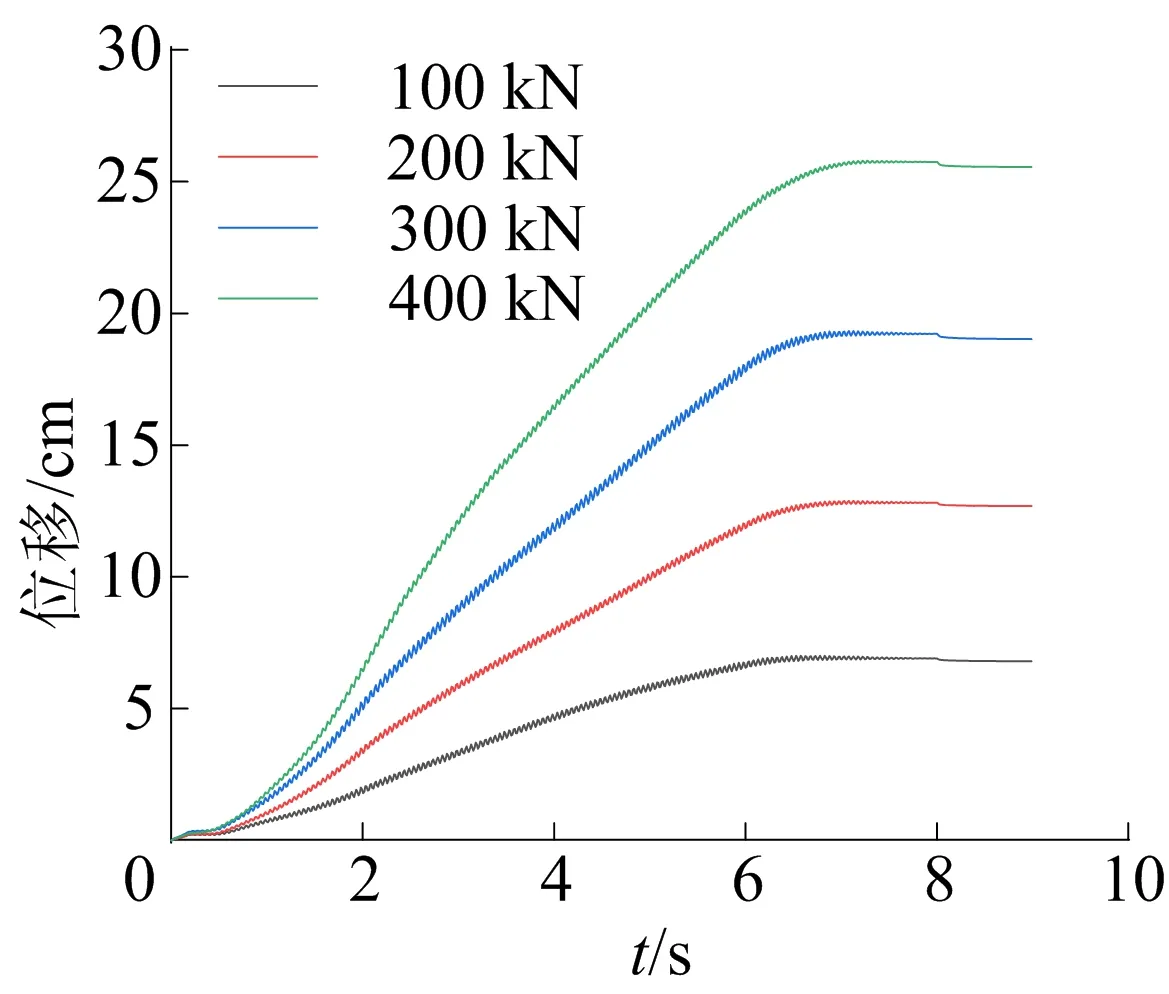
图13 不同拔桩力下钢管桩位移时程曲线

由图13可知,在上拔力作用下钢管桩以较快的速度上升,桩顶停止加载后位移达到一个稳定值,4种作用力下钢管桩的最终上拔位移分别为6.8、12.7、19.0、25.6 cm。本文钢管桩质量约为4 t,在振动锤使得桩侧土逐渐液化的情况下,钢管桩自重成为上拔阻力的主要因素,因此只要略大于钢管桩自重的上拔力即可使钢管桩有明显的位移。

以400 kN的上拔力为例,激振结束后持续施加静力上拔,得到计算时间步12 s时拔桩效果图如图14所示。

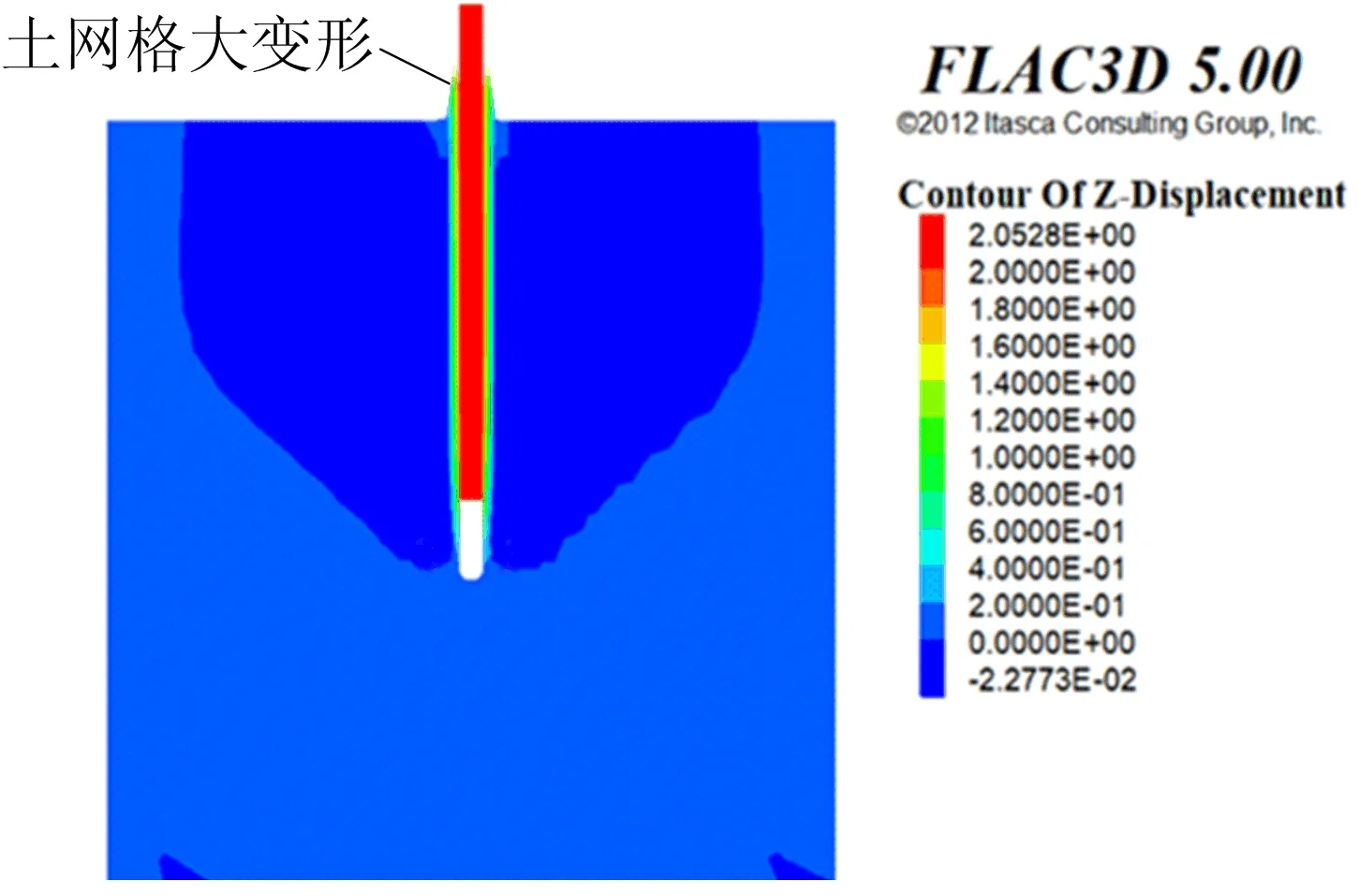
图14 拔桩效果图

此时钢管桩上拔位移可达2.05 m,由此可知采用EP160型振动锤进行拔桩的效果显著,桩侧土体网格由于大变形作用被钢管桩向上拖拽了一段距离,这也真实模拟出实际拔桩施工中桩侧土由于抗剪强度破坏而被拖出的现象。现场拔桩试验示意图如图15所示。在钢管桩一侧布置水准尺测量试验过程中钢管桩的位移,钢管桩在不同荷载下的位移与数值分析值对比如图16所示。从图16可以看出,上拔力与位移基本呈线性关系,说明桩侧土产生液化,钢管桩基本只受上拔力与自身重力,线性增加上拔力,上拔位移也线性增大。数值计算结果与实测结果误差较小,证明可以通过数值计算的方式对振动锤拔桩过程进行预测,为工程实际提供参考。

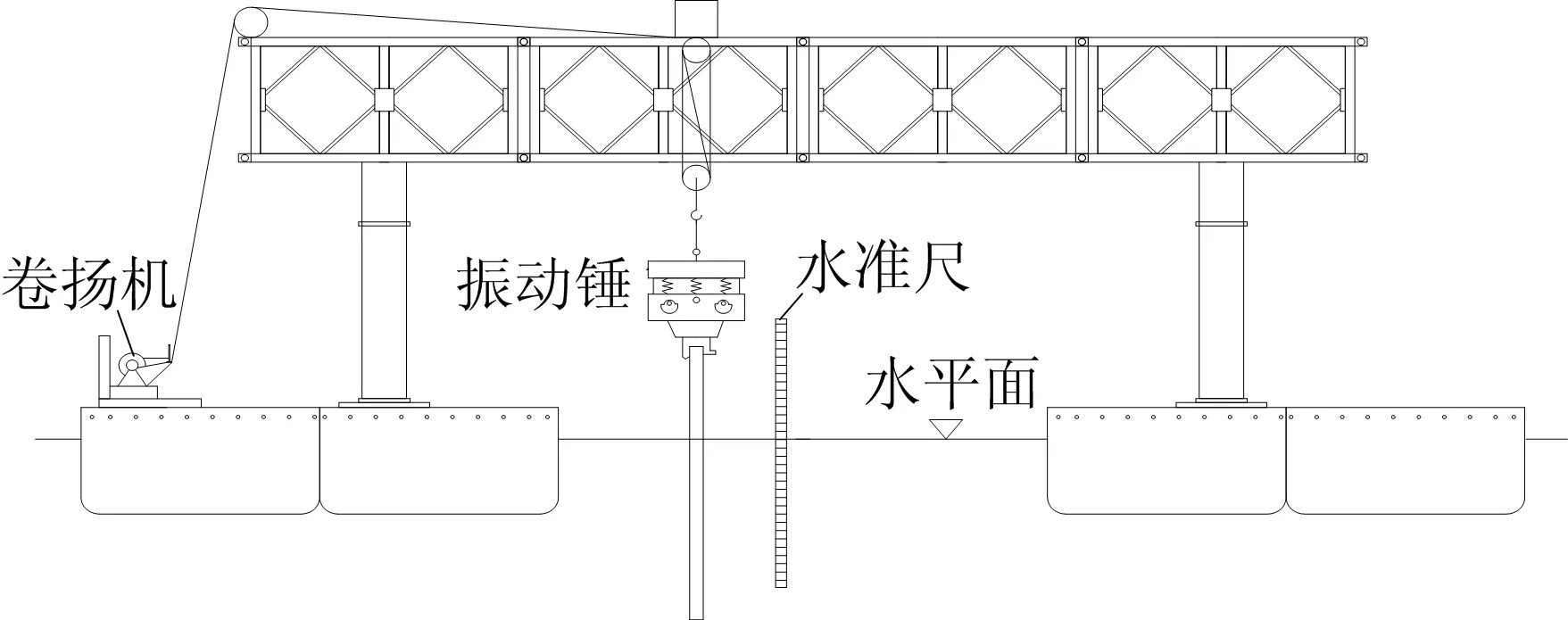
图15 拔桩试验示意图

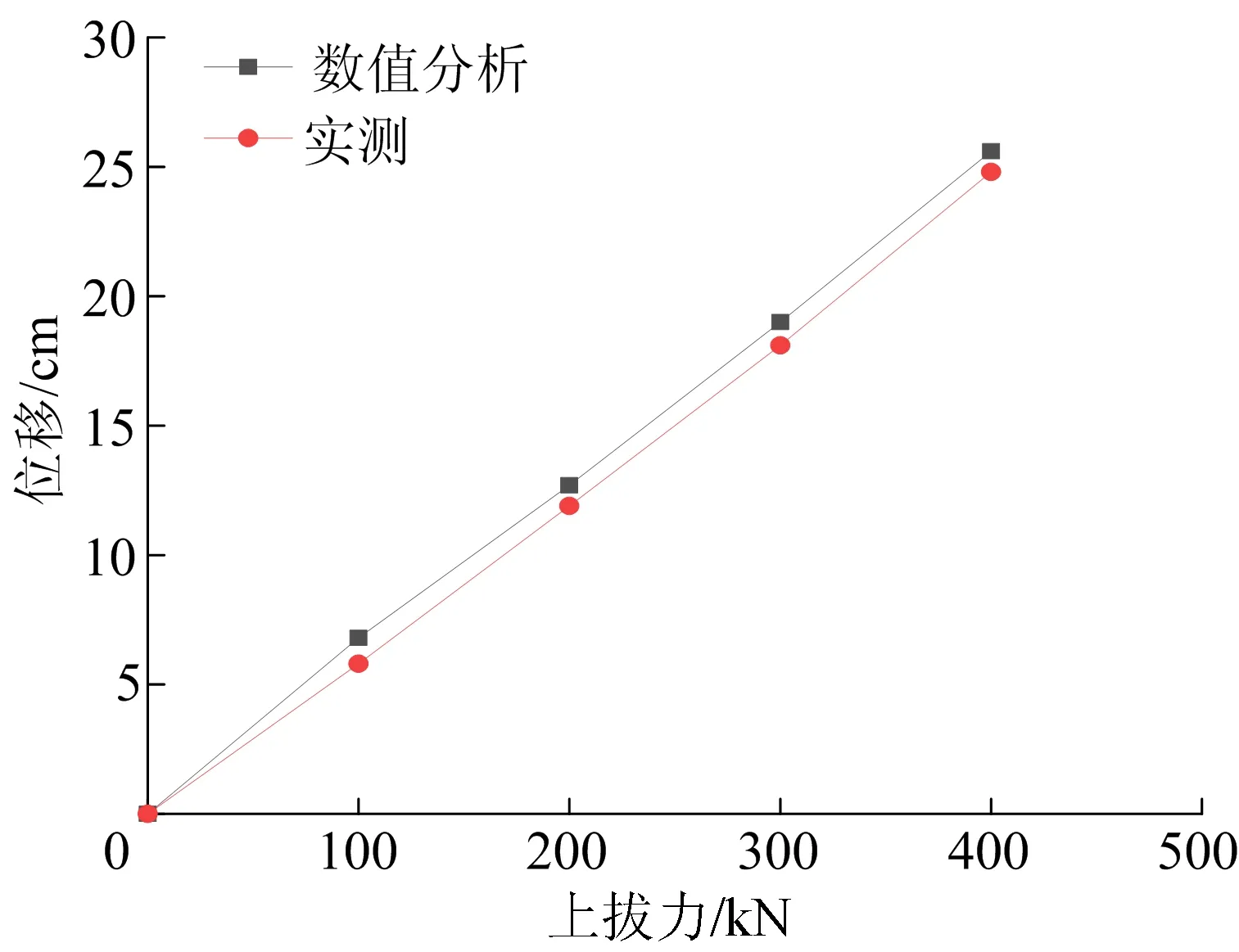
图16 不同上拔力下位移数值分析与实测结果对比

4 结 论

本文结合实际工程,建立振动锤拔桩的桩-土动力相互作用模型,分析桩侧土的液化效应,并对拔桩过程进行分析,得出以下结论:

(1) 对桩侧土的液化效应进行分析,监测各测点的超孔隙水压比,发现激振力作用下超孔隙水压比能很快达到最大值,且离振源较近的几个点最终超孔隙水压比接近于1,说明激振过程中桩侧土体孔隙水压力在增加,有效应力在减小,桩侧土产生液化,对各测点加速度响应的分析进一步证明桩侧土超孔隙水压比变化的规律。通过超孔隙水压比云图可直观判断出EP160型振动锤作用下桩侧土产生较大范围液化,说明EP160型振动锤振动效果较好,可有效降低拔桩阻力,能够运用于该工程的拔桩施工。对不同频率及振幅下桩侧摩阻力进行分析,结果表明在较高频、大振幅的作用下,桩侧摩阻力值均接近于0。

(2) 对振动锤拔桩过程进行分析,桩顶激振的同时施加上拔力,得到100、200、300、400 kN上拔力作用下,钢管桩的上拔位移分别为6.8、12.7、19.0、25.6 cm;桩侧土液化的情况下,施加上拔力钢管桩有较明显的位移,数值分析结果与现场振动锤拔桩试验所测上拔力-位移曲线吻合,验证了数值方法计算拔桩过程的准确性,桩侧土液化情况下,钢管桩位移基本只受上拔力与钢管桩自重的影响,因此上拔力与上拔位移大致呈线性关系。