基于多行为交互的变维协同进化特征选择方法

李腾飞， 冯 翔， 虞慧群

（ 1. 华东理工大学信息科学与工程学院，上海 200237；2. 上海智慧能源工程技术研究中心，上海 200237）

近年来，特征选择技术已经成为数据预处理特别是高维数据预处理中的一个重要技术。随着大数据时代的到来和网络技术的发展[1]，在许多机器学习应用中收集的特征数量变得越来越大。由于“维数诅咒”[2-3]的存在，传统的机器学习方法往往不能很好地处理高维数据。值得注意的是，随着维数的增加，数据空间中可能存在的实例数量也在极速膨胀，使得可用数据变得稀疏, 而这些数据的增长通常与有限元的数量成指数关系。更重要的是，并不是所有的特征都有用，与提供有用信息的特征不同，不相关特征提供误导信息，导致学习性能的下降。而冗余特征提供了与其他特征相同或相似的信息，浪费了大量的计算资源，严重影响了学习效率。因此，越来越多的学者开始探究更好的特征选择方法，进而从高维的原始特征集中剔除不相关的冗余特征以减少数据的维数，简化学习模型和提高算法的性能[3]。

粒子群优化算法(PSO)[4]是一种基于群体的全局搜索能力较强的算法，是用作特征选择的一种有效技术。目前，PSO 在特征选择中展现出了良好的应用前景[5]。然而，它的大多数应用通常是低维的，在具有数千个或更多特征的高维数据上的性能依然有限。

Liang 等[6]提出的综合学习粒子群算法（CLPSO）是连续粒子群优化算法的一种变体。该算法为每个粒子维持了一个样本池，粒子的每个维度参照样本池中的粒子编号进行学习，保持了种群的多样性，缓解了粒子群普遍存在的提前收敛问题。Qian 等[7]将概率模型和粗糙集嵌入标签重要性中，根据特征依赖和粗糙集，设计了一种新的多标签分类特征选择算法。Zhou 等[8]对每个特征进行基于熵的切点优先级排序，同时采用概率指导的局部搜索策略提升算法的性能。Huda 等[9]提出了新的初始化与更新方式，有效地提升了粒子群算法在特征选择上的性能。

Fister 等[10]将自适应差分算法与神经网络进行结合，取得了令人鼓舞的进展。Ji 等[11]提出了改进的PSO 算法（IBPSO），引入了局部搜索因子、全局搜索因子，同时采用变异策略维持种群多样性，取得了较大的性能改善。Chen 等[12]将PSO 算法与差分算法（DE）结合，提出了混合粒子群算法（HPSO-DE），差分算法用于维持群体多样性，提升算法的探索能力。Guan 等[13]提出了一种搜索历史导向的差分进化算法（HGDE），该方法利用存储在二叉空间划分树中的搜索历史来增强其选择特征组合的能力。Nguyen 等[14]提出由期望的最大特征数目确定每个粒子的维度，该方法所选出的特征子集远远小于典型解，不过难以确定期望的特征数量。Gu 等[15]提出的竞争粒子群算法（CSO）引入了粒子竞争行为，在大规模优化上展现出了良好的效果，然而算法的计算效率还有待优化。Tran 等[16]提出了可变维度的粒子表示方式，大大缩小了搜索空间。利用维度划分机制令PSO 可以跳出局部最优，取得了更小的特征子集和更高的计算效率。

本文受Tran 等[16]提出的变长粒子维度表示思想的启发，提出了一种基于多行为交互的变维协同进化特征选择算法(M-CVLPSO)。针对可变维度粒子群算法（VLPSO）初始化阶段的盲目性，采用连续空间上的层次初始化策略，使粒子分布更加均匀，从期望上缩短了初始解与最优解的距离。在更新阶段，根据适应度将粒子分为领导者、追随者与淘汰者，不同角色的粒子采用不同的更新方式，动态平衡算法各个阶段的多样性与收敛性。领导者的合作行为将群体知识从低维传向高维，有效解决了VLPSO的信息隔离缺陷。最后，将维度缩减率加入适应度函数中，进一步加强了M-CVLPSO 在部分数据集上的表现。

1 问题描述

全局优化问题可描述为在一个有限对象构成的解空间中找出最优解的一类问题。根据优化函数的优化目标，全局优化问题可以被分为最小值优化问题和最大值优化问题，而这两类问题又可以相互转换。

假设优化函数f(x) 具有m维变量 (x1,x2,···,xm) ，令X1=(x11,x21,···,xm1) 为m维变量的一个可行解，S={X1,X2,···,Xn}为所有可行解构成的解空间，则全局优化问题可以表示为求解f(x) 的最小值。

目标是找到一个可行解X*满足公式：

特征选择可以被表述为如下的最小全局优化问题：

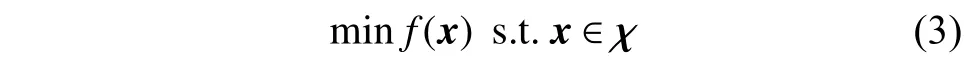
其中， χ ∈RN表示潜在可行解集。为了表示被选择的特征集，x采用长度为N的连续编码，N为原始特征集中的特征总数。对于x中的每一维，如果该维度上的值大于阈值，则代表该特征被选择，反之则为遗弃特征。这样，特征选择就变为了寻找最佳特征子集x*的组合优化问题，以最小化所选特征训练的分类模型的错误率。

2 M-CVLPSO 算法模型

2.1 VLPSO

2.1.1 粒子表示方式 VLPSO 采用基于综合学习粒子群算法（CLPSO）的变长粒子表示方法。基于变长表示，粒子的维度可以小于原始特征数目，该表示方法依然基于向量，不同种群的粒子具有不同长度的表示。图1 示出了VLPSO 模型的粒子表示方式。

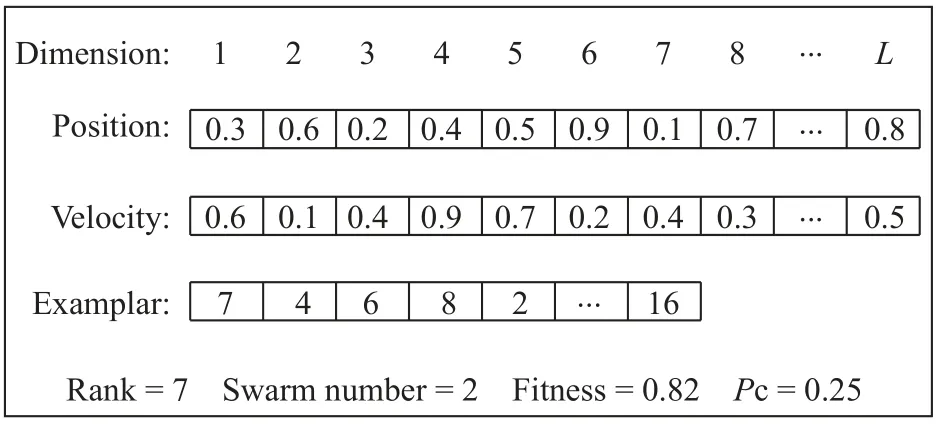
图1 基于CLPSO 的变长粒子表示示意图Fig. 1 Clpso-based variable-length particle representation

2.1.2 初始维度划分 由于不同种群的粒子具有不同的维度，因此需要对原始特征进行合理的划分。采用对称不确定度(SU)来计算特征与类标签的相关程度。假设原始特征数目为D，期望划分的种群数目为M，待初始化的粒子总数为N，从第一个维度开始依次计算特征X与类标签Y的对称不确定度Si。SU(X|Y)定义为

IG(X|Y) 为变量X与Y之间的依赖度，定义为

其中：H(X) 为变量X的信息熵；H(X|Y) 为变量X在给定Y下的条件熵。 S U(X|Y)∈[0,1]，X和Y的相关性与对称不确定度成正比。

按照Si从大到小对原始特征进行排序，并根据式（6）计算第m个种群的粒子维度:

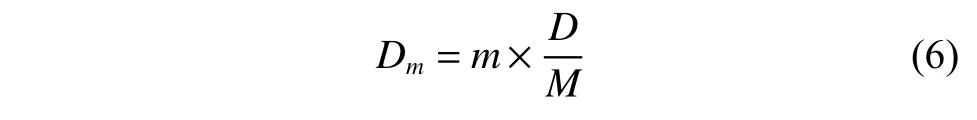
每个种群的粒子数目为

在排序后的原始特征中从前向后依次选择Dm个特征作为第m个子种群的原始特征空间。

2.1.3 初始维度划分 模型采用CLPSO 的更新过程，其中，粒子可以向群内的任意粒子学习，在每个维度上通过概率p决定粒子i选择自身还是另一个粒子作为学习样本，计算公式为

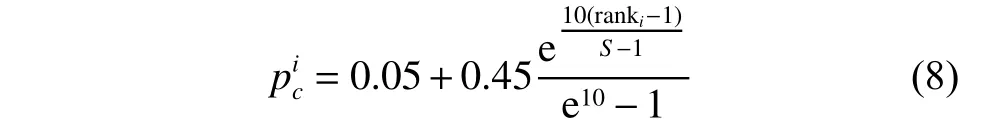
其中：S为种群规模； r anki为该粒子在种群中的适应度排名。

利用大小为2 的锦标赛机制为每个维度确定学习样本，一个粒子的学习样本将保持不变，直到该粒子连续未更新的代数超过设定的阈值。此时，将重新替换该粒子所有维度上的样本序号。CLPSO 速度更新公式如下：

其中：rid为 [ 0,1] 上的随机数； E xamplar为粒子i的学习样本在d维度上的值；w为惯性权重因子；c为社会学习因子；x代表粒子i第t代在d维度上的值。

2.1.4 维度重划分机制 为了使粒子群优化算法跳出可能的局部最优解，当全局最优粒子 g best 在预先设定的迭代次数下没有变化时，计算每个群体中所有粒子的平均适应度，标记当前最优种群为 S warmbest，保持 S warmbest粒子的维度 B estLen 不变，其余种群按照式(10)更新自身的维度：

其中：k为种群的序号，且不包括 S warmbest；M为种群数目。

若新维度小于原维度的种群，按照降序从末尾删除指定个数的特征；若新维度大于原维度的种群，按照升序从尾部挑选指定个数的特征加入。

2.2 层次初始化策略

VLPSO 模型采用完全随机的粒子初始化方式，导致初始粒子在解空间内的分布盲目且不均匀，降低了初始种群的探索能力。由于算法的后续求解都依赖于初始粒子在高维特征空间的探索，因此，初始群体的生成策略对后续的寻优过程有着潜在且深远的影响。初蓓等[17]在离散空间上提出了一种二向初始化策略，但其搜索方向仅为前向和后向，仍不能保证初始点在搜索空间的多向均匀分布。其次，本文采用的是连续表示的粒子群方法，需要提出一种连续空间上的多向初始化策略。为此，本文提出了一种层次初始化策略。

在种群进行初始化时，假设每个种群粒子数目为N，当前种群粒子的特征维度为D′，预期差异群体数目为Mdiv，则依次随机选中 「D′/Mdiv」 、 「 2D′/Mdiv」 、···、「(Mdiv-1)D′/Mdiv」维度的特征进行差异群体的粒子初始化。因为采用连续表示，不能简单地将维度置为1 或0，而是加入选择阈值 T hre 来帮助初始化。设某粒子待初始化维度为Di，则有

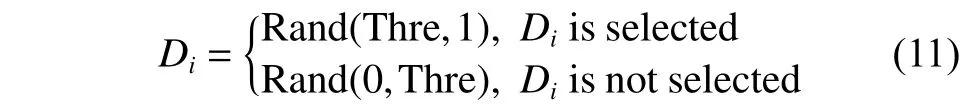
其中： R and(a,b) 表示区间 [a,b] 上的随机数。

每个差异群体的粒子数目均为N/Mdiv。图2 示出了层次初始化策略下的粒子分布，红点代表理论最优解，层次初始化策略将初始群体均匀散布在不同维度的搜索空间，增强了初始粒子群体的多样性以及后续的探索能力，一定程度上降低了随机带来的盲目性。

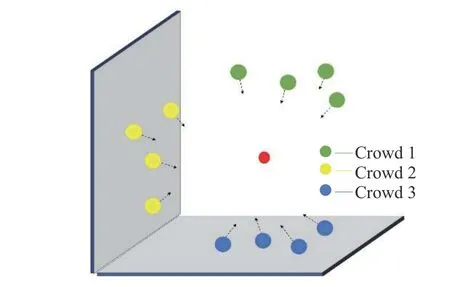
图2 层次初始化Fig. 2 Hierarchical initialization

2.3 多行为交互策略

VLPSO 模型在进化过程中对所有粒子采用单一的更新策略。然而，多项研究表明适应度较差的粒子应该加强其全局探索行为的比重，而适应度较好的粒子应该加强其局部探索行为的比重，因此，不同适应度排名的粒子所需要的更新行为是不同的。本文根据适应度排名将粒子分为领导者（排名在前20%）、追随者（排名在20%～75%）与淘汰者（排名在后25%），提出了一种包含竞争、合作与同化的多行为更新策略。根据进化过程中粒子适应度排名的变化，自适应采取不同行为来完成粒子的更新。

2.3.1 竞争行为 淘汰者采用竞争行为进行更新。在每一代进化结束后，环境均会对粒子的适应度进行评判，并淘汰部分粒子，这样更加有利于维护进化群体的质量，以快速寻找到最优解。新生粒子的产生可以借鉴已有的知识，站在“巨人”的肩膀上能够保证新生粒子的质量。

因为采用变长表示，因此不同种群探索的解空间不同，粒子与粒子的竞争主要存在于单个种群的内部。设第m个种群内的粒子数目为Nm，在具有淘汰行为的种群中，对于淘汰粒子k的每个维度，在领导者中随机选取两个粒子xi,xj，设 R ankxi＞Rankxj，更新公式如下：

其中：f1和f2为自适应系数； R ankxi和 R ankxj分别为粒子xi、xj在种群中的适应度排名。

这种粒子更替策略使目标粒子不会完全被单一粒子所吸引，增强了生成粒子的多样性和群体的全局探索能力。同时由于目标粒子对群体中优秀粒子知识的继承性，保证了新生粒子的质量。

2.3.2 合作行为 领导者采用合作行为进行更新。VLPSO 采用了多种群寻优，却完全隔离了彼此间的信息，浪费了大量的优秀知识。由于低维群体探索更小的特征空间，相同迭代次数内在交叉维度上通常较高维群体能够找到更优的特征子集，因此，为了有效利用已有知识，让高维群体的领导者借鉴低维群体领导者的交叉维度，将知识从低维传向高维。

首先，将所有种群按照粒子维度从小到大排序，设待更新种群序号为i，将序号为i-1 的种群按照粒子适应度进行排序，得到 S warm。选定待学习的高维粒子XHV，假设排名为k,将 S warm中所有适应度高于XHV的粒子加入到样本池中，如果这样的低维粒子共有c个，则设样本池ExamplarXHV={X1,X2,···,Xc-1,Xc} 。若 E xamplarXHV为空，且满足p＜p，则按照式（14）对XHV所有维度进行更新：

其中：c1为常数；r1和r2为 [ 0,1] 之间的常数；Pbestd为粒子i历史最优值d维度上的值；p为利用式（8）计算的学习概率；p为 [ 0,1] 上的随机数。

若p＜p，利用所属种群样本池进行更新。如式（15）所示：

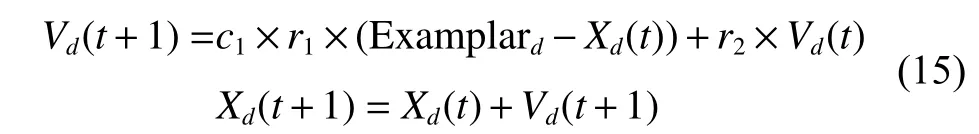
其中： E xamplard为学习样本d维度的值。

若 E xamplarXHV不为空，对XHV与低维样本池交叉的维度利用低维度种群生成的样本池进行更新，并且概率判断总是成立；对XHV独有的维度，利用所属种群样本池进行更新。两种情况下的更新公式均同式（15）。

可以看出，仅当低维群体存在适应度优于待更新个体的粒子时，才会将交叉维度的样本池替换为低维群体，否则，仍然利用待更新粒子在所属种群中生成的样本池更新所有的维度。

2.3.3 同化行为 追随者采用同化行为进行更新。在种群进化的过程中，劣势粒子更加倾向于向种群内部的其他优秀粒子学习。本文借鉴社会学习粒子群算法（SL-PSO）[18]的思想，引入社会平均影响的概念，其实验已经表明该因子能有效平衡粒子的多样性和收敛性。设待更新的粒子为Xi，所属种群为Swarmj,则该种群的社会平均影响为

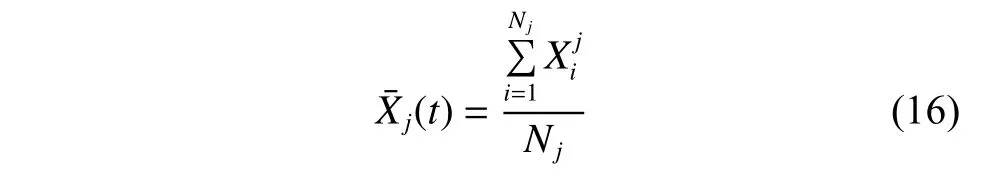
其中：Nj为该种群的粒子数目。

对当前种群进行适应度排序，序号越低的粒子适应度越大，不同种群的序号独立，排序后的种群为Swarmsort_j，生成Xi的样本池ExamplarXi={X1,X2,···,XrankXi-2,XrankXi-1} ，设待更新为维度d，若满足p＞p，则有

若p＜p，则从 E xamplarXi中随机选择一个学习样本 E xamplari，粒子更新公式为

其中：r1、r2、r3为 [ 0,1] 之间的常数； P best为粒子i历史最优值d维度的值； ε 为引诱系数； β 为常数；ParSizei为粒子i的维度，粒子i属于种群j；Nj为第j个种群的粒子个数。

图3 示出了多种行为在不同维度群体间的作用方式。种群内部进行淘汰和同化行为，种群间由领导者进行合作行为，共同完成种群的迭代更新。

图3 多行为交互策略下的粒子更新示意图Fig. 3 Particle update under multi-behavior interaction strategy

2.4 适应度函数

虽然分类精度可以度量特征子集的性能，但是仍有许多潜在的局限性。 Tran 等[16]提出了结合分类精度与实例间距离度量distance 的适应度函数评估方法，考虑了特征子集区分各类别实例的程度，定义为

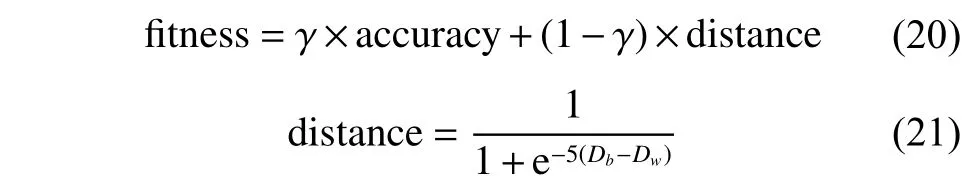
针对类间距离Db的计算公式，以实例到类外粒子的最小距离作为参考，取其平均值来评估该特征子集对不同类别实例的分离程度，定义为

而类内距离Dw以实例到类内粒子的最大距离作为参考，取其平均值来评估同一类粒子间的聚合程度：

该适应度函数旨在最大化不同类别实例之间的距离，最小化同类别实例之间的距离。

维度缩减也是特征选择问题中需要关注的，更少的特征意味着更小的冗余、更高的计算效率。基于此，本文提出了一种新的适应度函数，定义如下:

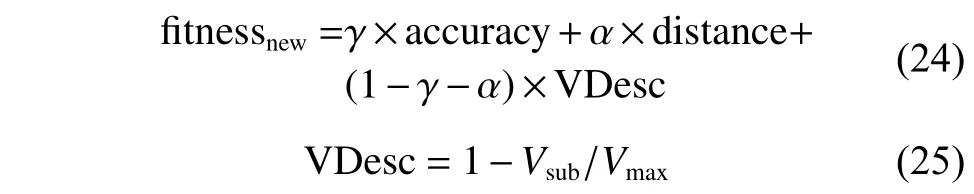
其中： γ 、 α 为待设定的参数；accuracy 为分类精度；Dis(Ii,Ij)为粒子Ii和Ij距离衡量公式；class(Ii)为粒子Ii的分类结果； V Desc 为维度缩减率；Vsub为特征子集的维度；Vmax为当前所有种群中的最大特征维度。

该适应度函数在分类精度与实例类间距离相近的状况下，会优先选择维度较小的粒子。因此，在维度重划分时，低维种群更容易成为最优种群，从而在一定程度上更快地降低群体的平均维度，加速模型的迭代进程。但是，分类精度与类间距离仍然是主要的选择标准，因此后期应分配更小的权重。

2.5 收敛性证明

与大多数粒子群优化算法理论收敛性分析相似[19-20]，本文从理论上分析M-CVLPSO 模型的收敛性。应该指出的是，证明并不保证收敛到全局最优。

在不失一般性的前提下，整个群体的收敛可以更具体地看作是任意粒子行为向量中各维的收敛。理论上，应该存在一种平衡来诱导这种收敛[21]。考虑粒子i(1 ≤i≤m) 第d(1 ≤d≤n) 个维度的更新，一旦满足p＜p，X(t) 将会通过式（26）进行更正：

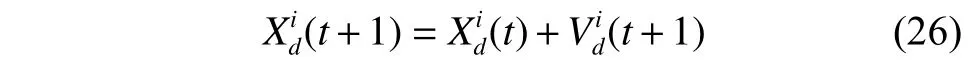
同理，将式（18）代入式（26），并替换所有随机参数为其期望值，可以得到：

定理1 式（27）与式（28）描述的动态系统收敛于平衡状态。

证明 对式（27），令 θ =，p=Examplar(t) ，则式（27）可以被重写为

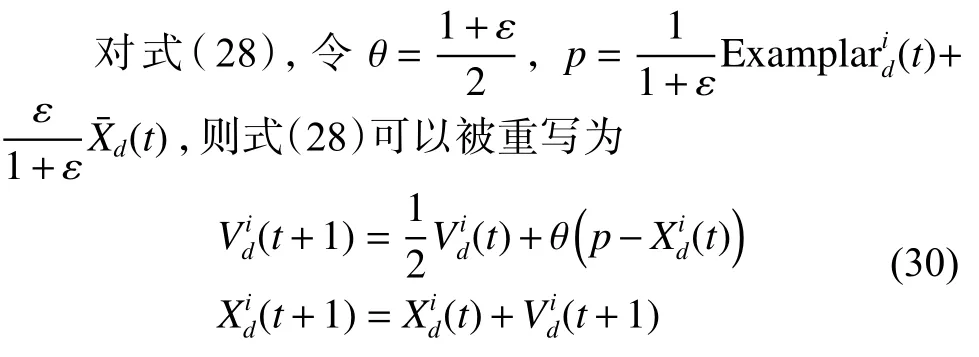
可以发现，两式的基本形式是一致的，因此可以统一验证其收敛性。式（30）中描述的搜索系统可以看作是一个动态系统，因此可以利用动态系统稳定性理论对系统进行收敛性分析。为此，将式（30）描述的系统重述为

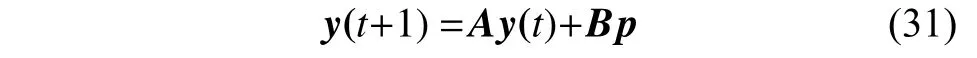
其中：A在动力系统理论中称为状态矩阵；p为外部输入，驱动粒子行为向量到达特定状态；B为输入矩阵，控制外部环境对粒子动力学的影响。

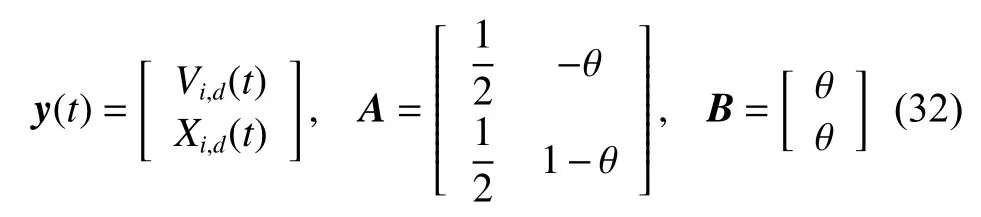
如果存在一个平衡y*对任意t满足y*(t+1)=y*(t)，可以从式（31）和式（32）中计算出

收敛性取决于状态矩阵A的特征值:

其特征值为

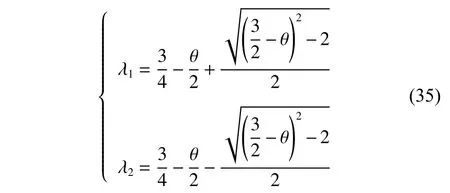
平衡点是一个稳定吸引子，其收敛的充要条件是 | λ1|＜1 并且 | λ2|＜1 ，可以得到

将 ε 利用 ε =β×(ParSizei/Nj) 替换为 P arSizei，条件转换为

2.6 M-CVLPSO 模型框架

本文针对VLPSO 随机初始化的盲目性、更新策略的单一性问题，分别提出了层次初始化策略和多行为交互策略。M-CVLPSO 算法的伪代码如下：

输入：最大迭代轮数T，种群个数NbrDiv，最大未改进轮数k

输出：特征子集向量

3 实验与分析

实验环境：实验中所用编程语言为Java，JDK 版本为1.8。实验计算机配置为CPU：Intel Core i7(2.2 GHz)，内存大小：16 GB，固态大小：512 GB。

3.1 数据集

在11 个UCI 公开数据集上对M-CVLPSO 算法的性能进行测试，表1 给出了数据集的具体信息。其中，#Features 表示数据集的维度，#Ins 表示实例数量，#Class 表示类别数目，%Smallest class 和%Largest class 分别表示实例数量最少和最多的类别占总实例数的比重。对每个数据集的划分采用10 交叉验证方式。以测试集的分类准确率（Classification Accuracy，CA）和平均类间距离（Classification Mean-Distance，CMD）作为评价准则。CA 是正确分类的实例数占总实例数的比例，即分类精度；CMD 是两两分类实例间的平均间距，代表了分类模型的鲁棒性及泛化能力。

表1 实验数据集Table 1 Experiment datasets

3.2 对比算法

为了验证M-CVLPSO 算法的性能，将其与目前表现最好的同领域算法进行对比，其中，具有代表性的有原始粒子群算法(PSO)[4]、综合学习粒子群算法(CLPSO)[6]、增强综合学习粒子群算法(ECLPSO)[22]、可变维度粒子群算法(VLPSO)[16]等。在大规模以及超大规模的数据集上从寻优精度、维度缩减能力以及计算效率3 个方面验证每个算法的特征选择能力。各个算法的公共参数保持一致，以确保实验的公平性，详细参数设置如表2 所示。其中，curr_iter 代表当前迭代轮数，max_iter 代表设置的最大迭代轮数。

表2 参数设置Table 2 Parameter setting

3.3 实验结果与分析

由于粒子群优化算法是一种随机算法，因此针对每种方法在每个数据集上分别运行10 个10 交叉验证。一个10 交叉验证包含10 次完整的运行结果，取这10 次完整运行结果的均值作为该次10 交叉验证的结果。算法单次10 交叉验证均采用不同的随机数种子，但不同算法间保持随机数种子的一致，100 次实验结果的均值如表3 所示。其中，Time 表示算法在该数据集上的单次平均运行时间，更少的时间代表更高的运算效率；Size 表示最优特征子集的平均维度，越小的维度代表更高的维度缩减能力；Best 表示10 次10 交叉验证中出现的最优单次10 交叉验证平均分类精度；Mean 则为10 次10 交叉验证的平均分类精度；Full 代表原始特征集的分类结果。表4 示出了各个算法在4 个性能指标上的friedman 排名，图4 示出了各个算法在11 个数据集上的详细性能指标排名情况。

图4 5 种算法在11 个数据集上的各项指标排名Fig. 4 Ranking of the five algorithms on eleven datasets

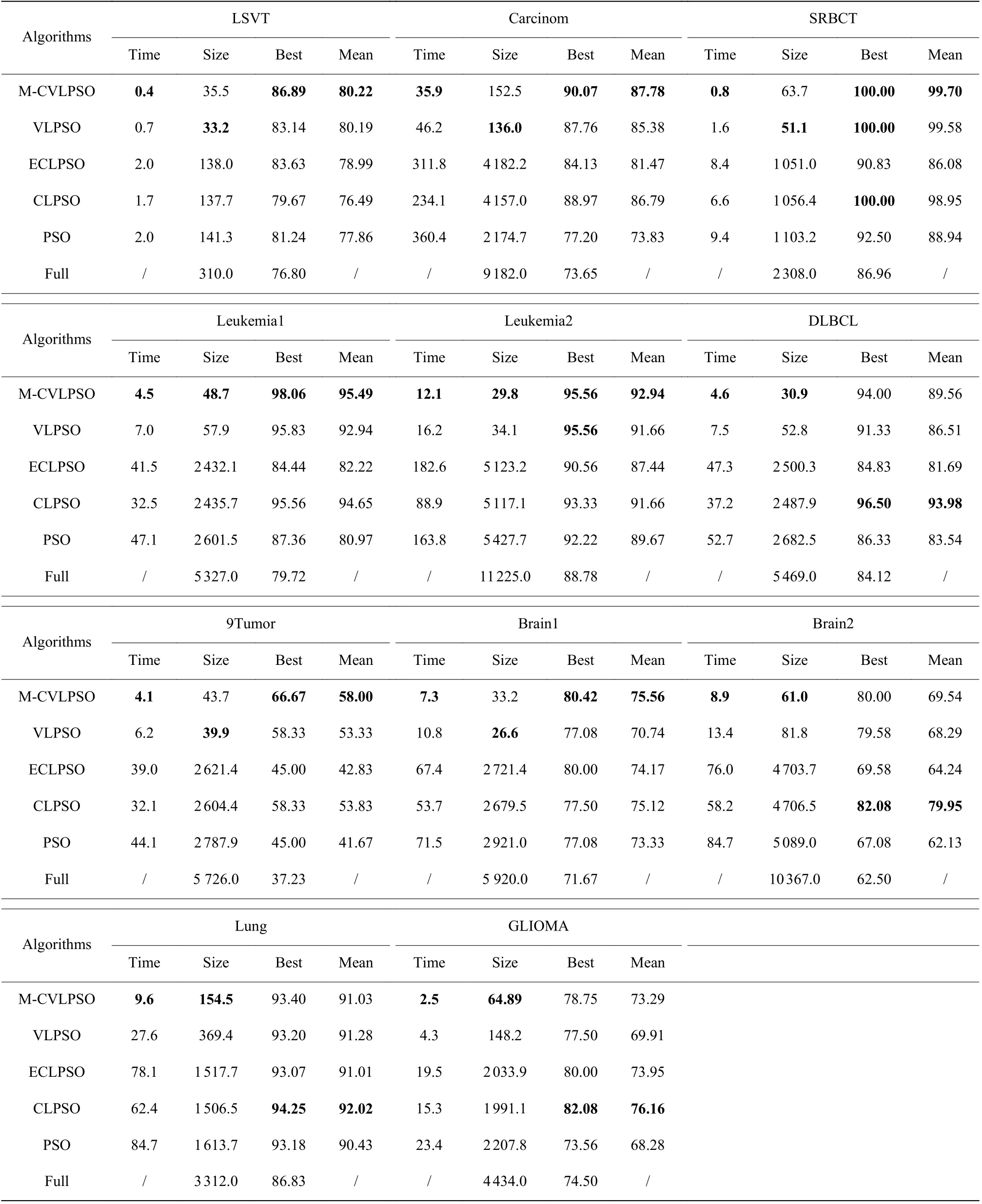
表3 平均测试结果Table 3 Average test results

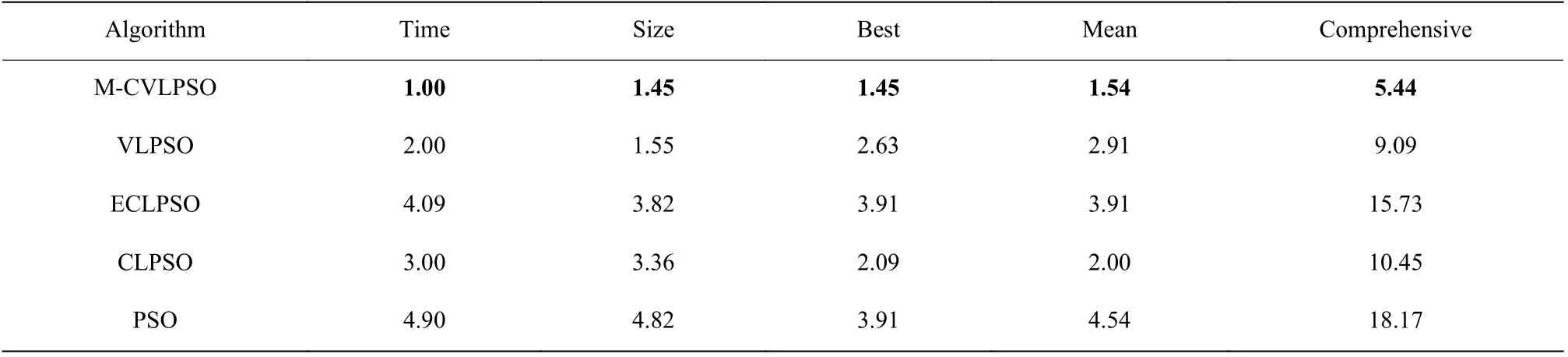
表4 5 种算法在特征集上的平均Friedman 排名Table 4 Average Friedman ranking of the five algorithms on the feature set

从特征子集的维度（Size）来看，PSO、CLPSO 和ECLPSO 均高于M-CVLPSO 若干倍。在维度较低的数据集上，如LSVT、SRBCT 等，通常在20 倍以内，而在超大规模数据集上，如Leukemia1、Leukemia2、Brain1、Brain2、DLBCL、9Tumor 等，最高可以达到170 倍。与VLPSO 相比，M-CVLPSO 在7 个数据集上的平均维度低于VLPSO，其中在GLIOMA、Lung、DLBCL、Brain2 上的缩减相当明显，最高减少了一半以上的维度。而在剩余的5 个数据集上，M-CVLPSO与VLPSO 表现相当，VLPSO 的平均维度略低于MCVLPSO。

从寻优的时间复杂度（Time）来看，M-CVLPSO模型在11 个数据集上的表现最好。PSO、ECLPSO和CLPSO 均高于M-CVLPSO 至少5 倍以上的时间。而与VLPSO 相比，这个倍数在1.3～2.8。分析原因，一是采用了变长维度的表示方法，而低维度粒子相对于高维度粒子拥有更高的更新计算效率；二是相对于VLPSO，多行为交互的更新方式，能够更快地缩减种群的平均维度，减少了在高维空间探索的代数，从而降低了计算时间。图5 示出了各个算法寻优过程中种群平均维度的变化情况。

图5 各种算法种群平均维度随迭代变化曲线Fig. 5 Average particle dimension of different algorithms varies with iteration

从寻优精度来看，在最佳寻优精度（Best）上，MCVLPSO 在7 个数据集上取得了最好的结果，获得了

最高8%的提升。在3 个数据集上取得了第二，与第一最高相差2.5%。在GLIOMA 数据集上表现较差，排名第三，与CLPSO 相差3.33%。 CLPSO 在GLIOMA、Brain2、Lung、DLBCL 上的最优精度略高于M-CVLPSO，但是特征子集的维度和寻优的时间复杂度远远高于M-CVLPSO。

平均寻优精度（Mean）方面，M-CVLPSO 依旧在7 个数据集上取得了第一，最高提升4.67%，同时在Brain2、DLBCL 上取得了第二名。而在GLIOMA、Brain2、DLBCL 数据集上，CLPSO 表现强势，取得了第一。各算法在寻优过程中的最优粒子适应度曲线变化情况如图6 所示。

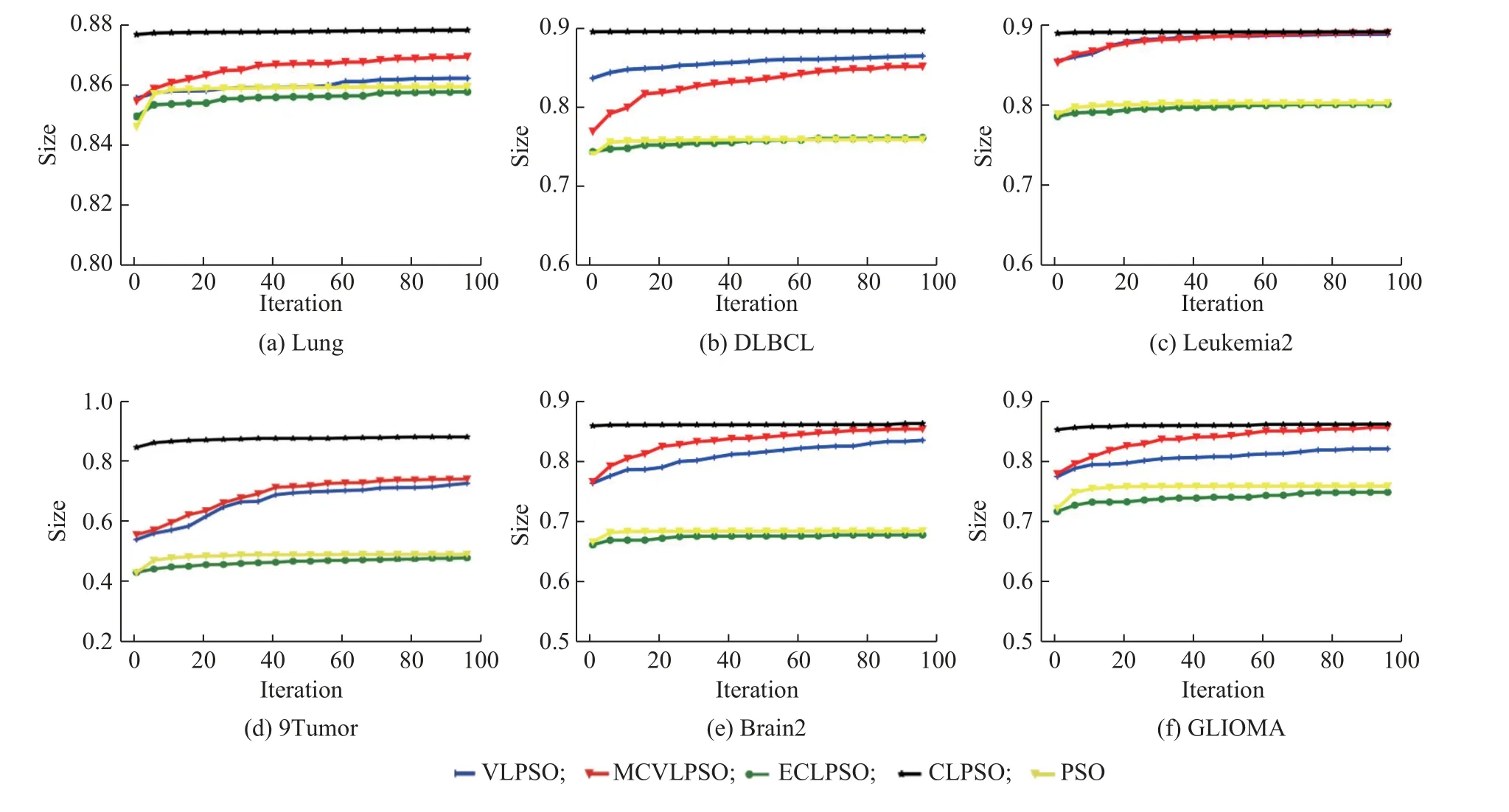
图6 各种算法最优粒子适应度变化曲线Fig. 6 Optimal particle fitness curves of different algorithms

3.4 新适应度函数的有效性分析

从3.3 节的实验结果可以看出，在DLBCL、Lung、Brain2 以及GLIOMA 数据集上，M-CVLPSO 的精度没有达到最好。从粒子的维度来分析，发现在这4 个数据集上M-CVLPSO 模型的平均粒子维度远小于包括VLPSO 在内的其他算法，可能是模型在后期仍在探索新的维度空间而在有限代数内未能及时收敛。因此，在适应度函数的计算中加入了维度缩减率，期望在前期更快地降低种群维度，从而使模型有更充分的代数进行低维空间上的探索。同样，在MCVLPSO 中使用新的适应度函数在上述4 个数据集上进行10 个10 交叉验证，表5 示出了100 次实验的平均值。其中，I 是未加入维度缩减因子的模型，II 是加入了维度缩减因子的模型，ALL-Best 则代表表3中所有模型在该数据集上能够取得的最好结果。可以看出，在这4 个数据集中，其在DLBCL、Lung和Brain2 上的结果均优于M-CVLPSO，且在最优精度上高于原来所有模型的最优值。不过，在平均精度上其相较于M-CVLPSO 有所提升，仍然低于原来的最优平均精度，而在粒子维度与运算时间上则基本相当。从实验结果来看，维度缩减率能够影响模型分类精度，且对于大规模数据集上的提升较为明显。

表5 加入新适应度函数的平均测试结果Table 5 Mean test results with new fitness function

3.5 层次初始化策略的有效性分析

为了验证层次初始化策略的有效性，使用未加入该策略的M-CVLPSO-Without 算法进行10 交叉验证，每次实验只进行一轮迭代，对10 次实验结果的最优粒子适应度（Gbf）、最优粒子维度（Gbs）以及平均粒子适应度（Avf）求平均值，结果如表6 所示。可以看出，在绝大部分数据集上，加入了层次初始化策略后，在一轮迭代后最优粒子适应度与平均粒子适应度取得了较大幅度的提高，提升幅度通常在0.03～0.04。而在最优粒子的维度上表现与随机初始化相当。这表明层次初始化策略能有效提高初始化粒子的适应度，但对粒子的维度缩减无明显提高。

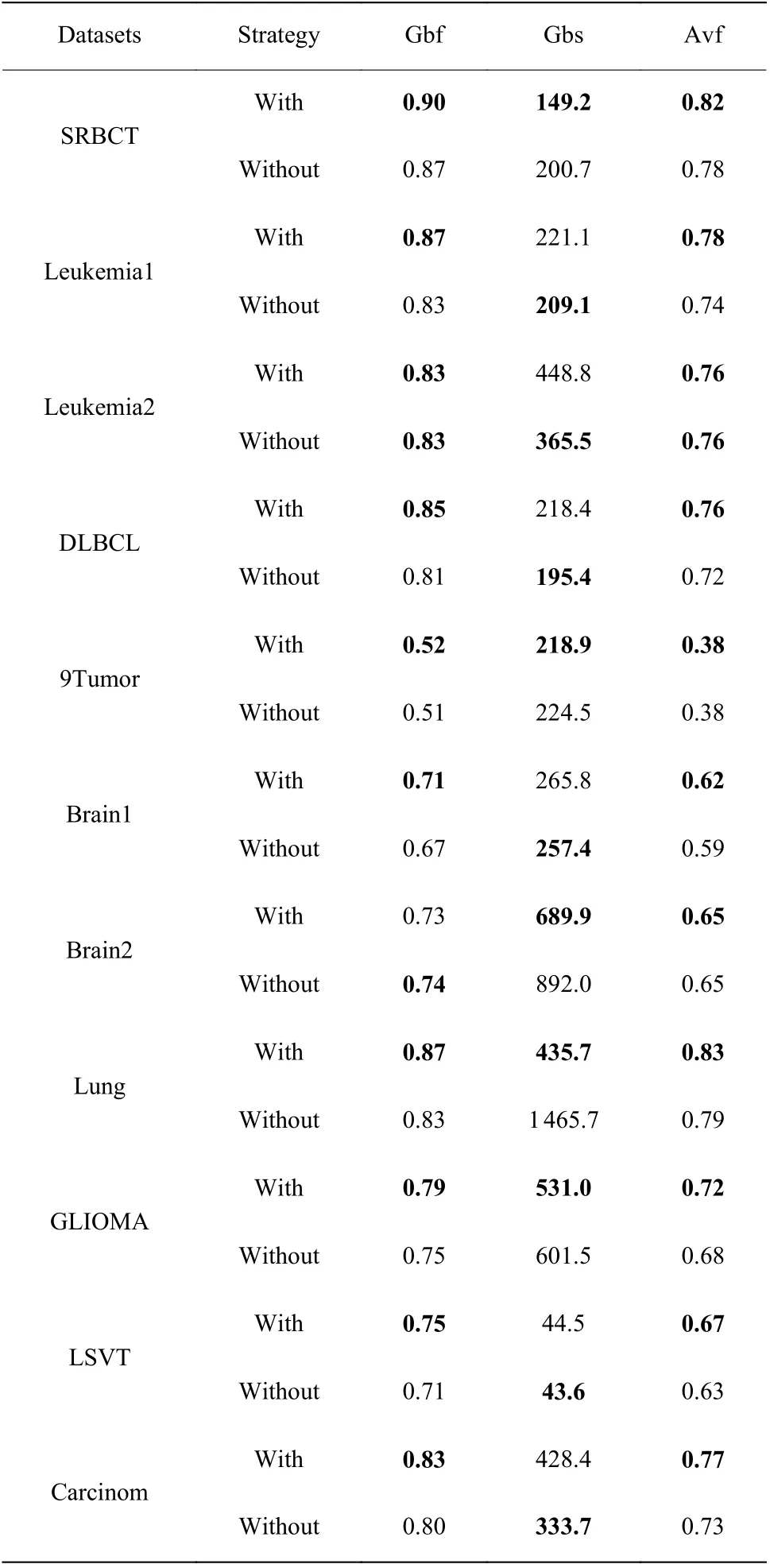
表6 层次初始化单轮迭代平均测试结果Table 6 single-round iteration average test results

同时，对仅加入层次初始化模块的模型I′进行5 次10 交叉验证，所用的随机数种子和公共参数与VLPSO 保持一致。对50 次实验结果取平均值，得到的各项数据如表7 所示。

表7 层次初始化策略消融实验结果Table 7 Ablation experiment results with hierarchical initialization strategy

可以看出加入了层次初始化后，相较于VLPSO，模型I'在9 个数据集上取得了更好的最优精度，最高提升4.53%，平均提升1.63%；在8 个数据集上取得了更好的平均精度，最高提升6.58%。而在LSVT、Leukemia2 和SRBCT 数据集上则是小幅度低于原算法。从时间和维度来看，与原算法基本一致，表明层次初始化能整体上提升粒子适应度，更容易在有限次迭代内找到更好的特征子集，而在维度缩减性能上并无提升。

3.6 多行为交互策略的有效性分析

对仅加入多行为交互模块的模型II'进行5 次10 交叉验证，所用的随机数种子和公共参数与VLPSO保持一致。对50 次实验结果取平均值，得到的各项数据如表8 所示。

表8 多行为交互策略消融实验结果Table 8 Ablation experiment results with multi-behavior interactive strategy

可以看出加入了多行为交互策略后，相较于VLPSO，模型II'在9 个数据集上取得了最优精度，最高提升5.42%，平均提升2.60%，而在9Tumor 与Brain1 数据集上略低于原模型。从时间上看，新的更新方式大大减少了运行时间，提高了计算效率。从维度上看，在DLBCL、Lung 和GLIOMA 数据集上模型II'取得了较大幅度的提升，在其他数据集上则基本相当。

同时，对5 种算法在每个数据集上100 次实验的迭代过程进行分析。因为迭代过程取决于所使用的更新方式，因此可以探究多行为交互策略的有效性。将100 次实验过程中每轮迭代的种群平均维度、最优粒子适应度横向求平均值，迭代曲线如图5、图6 所示。取特征数目差异较大的6 个数据集进行展示，更好地探究算法在不同规模数据集上的性能。

可以看出，相对于VLPSO，M-CVLPSO 能更快地降低种群的平均维度，有效地提高了计算效率，因此大大缩减了寻优的时间。而在最优粒子的适应度上，M-CVLPSO 也在4 个数据集上取得了更好的平均结果，仅在DLBCL 数据集上弱于VLPSO。而表3的实验数据也表明，M-CVLPSO 最优粒子代表的特征子集在多数数据集的分类中取得了更高的精度。与其他模型相比，M-CVLPSO 在种群维度缩减性能上大幅度领先于PSO、ECLPSO 与CLPSO，而在最优粒子适应度上大幅度领先于PSO、ECLPSO，低于

CLPSO。不过由CLPSO 最优粒子的曲线和表3 的寻优结果可以看出，该算法出现了PSO 算法的过早收敛问题，导致过拟合现象的产生，从而影响了在测试集上的泛化能力。

4 结束语

针对大规模数据集上的特征选择问题，提出了一种基于多行为交互的变维协同进化特征选择方法。首先，提出了连续空间上的层次初始化策略，从期望上缩短了初始解与最优解的距离，一定程度上克服了因随机带来的盲目性。在更新阶段，通过适应度将粒子分为领导者、追随者与淘汰者，不同角色的粒子采用不同的更新方式，动态平衡算法各个阶段的多样性与收敛性。领导者的合作行为将群体知识从低维传向高维，有效解决了VLPSO 的信息隔离缺陷。最后，将维度缩减率加入适应度函数中，进一步加强了M-CVLPSO 在部分数据集上的表现。基于11 个大规模特征选择数据集在分类精度、维度缩减和计算时间上进行实验分析，相比于4 种对比算法，M-CVLPSO 具有更好的综合表现。本文主要探究了该方法在大规模数据集上的综合特征选择性能，针对具有特定特征，如非平衡大规模数据集上的探索将是下一步的研究方向。