并排塔器的横风向激振特性与非光滑表面减振

2022-04-26谭蔚王中辰樊显涛唐博文

化工进展 2022年4期

谭蔚，王中辰，樊显涛，唐博文

（天津大学化工学院，天津 300350）

塔器是化工操作单元中的重要设备，在化工装置中的投资比例高达25%～46%。目前，关于塔器过程强化及节能优化的研究取得了丰富的研究成果，在此基础上，确保塔器的安全稳定运行则具有重要意义。随着塔器向大参数化和集约化方向发展，其普遍呈现高耸柔性特征，且布置愈加密集，其中固定在同一基础上，相互之间距离较小且按顺序排成一行的塔器被称为并排塔器。与单座塔器相比，并排塔器在风载荷作用下的横风向振幅更大，振动机理更加复杂，更易发生破坏。因此，采用非光滑表面被动减阻技术，通过调控塔器周围流场分布，以期实现塔器减振，对于并排塔器的防振以及化工行业的安全高效运营发展有着重要的理论价值和工程意义。

并排塔器横风向振动的本质是多圆柱的绕流问题。Igarashi将串列双圆柱的流动模式划分为/=1～2 的单钝体结构、/=2～5 的剪切层再附着行为以及/＞5的共同脱落行为。Assi等通过水洞实验解释了串列多圆柱的振动机理，并提出尾流刚度的概念来解释下游圆柱升力的产生。Kim 等开展了串列双圆柱风洞实验，确定了五种振动状态。Qin 等对串列双圆柱的流致振动进行实验研究，确定了四种振动状态，并发现下游圆柱的振动取决于上游圆柱的初始状态。及春宁等对各工况下串列多圆柱的涡激振动响应进行了数值模拟研究，详细分析了其振动响应和耦合机制。Fan等通过数值模拟和大气边界层风洞实验，分析了串列三圆柱的振动模式与涡结构对流致振动的影响。

为了有效解决并排塔器的风致振动问题，本质上应通过调控塔器周围流场来避免周期性卡门涡街的产生。Huera-Huarte 等在研究不同沟槽结构的紊流减阻时发现，通过选取合适的沟槽形状可以达到减阻的最佳效果。常跃峰等实验证明了沟槽壁面可以有效削弱湍流的流向、展向脉动和湍动能的生成。Choi等通过实验研究发现高尔夫球的凹坑通过造成不稳定的气流边界层，使球体的升力增大。彭恒等进行了高耸单座塔器的减振分析，国内学者对各类阻尼器的减振机理与性能分析进行了深入的研究，破涡翅片（包括螺旋翅片和轴向翅片）也已广泛应用于单座塔器的减振与防振。然而关于并排塔器非光滑表面减阻技术的研究依旧较为缺乏，对微型翅片的横风向减振特性仍需深入研究。

本文在间距比/=1.3～8 范围内开展了风洞实验，对亚临界区雷诺数下并排塔器的横风向振动特性以及微型翅片的减振特性进行研究，旨在为并排塔器的振动分析和防振设计提供依据和参考。

1 实验装置设计

1.1 实验模型

并排塔器是自支撑式柔性结构，处于亚临界雷诺数，具有高径比大、固有频率和阻尼比小的特点，在保证雷诺数相似和弹性准则相似的基础上，其横风向振动可以简化为由弹性支撑的多圆柱结构的横流向振动。因此，实验模型设计如下：塔器模型选用有机玻璃材质，其外径=25mm，高度=430mm，高径比为16.8，壁厚=2mm。模型通过弹性片（材质为65Mn）与框架连接，从而实现其沿横风向的单自由度振动。采用自由衰减法测量实验模型的模态参数，步骤如下：给结构施加一个冲击载荷，使其发生自由振动，得到其自由振动衰减曲线，如图1所示。利用式(1)计算阻尼比，将加速度时程曲线经过快速傅里叶变换后即可获得固有频率，如图2所示。计算得到实验模型的模态参数如表1所示。

表1 实验模型模态参数表

图1 塔器模型自由振动衰减曲线

图2 塔器模型加速度频域曲线

式中，̈为第个加速度振幅幅值，m/s；̈ 为第+个加速度振幅幅值，m/s；为阻尼比。

雷诺数定义为流体惯性力与黏性力之比，其表达式见式(2)。

式中，为空气密度，kg/m；为空气黏度，Pa·s；为来流风速，m/s。

本文采用弹性支撑的刚性截断模型进行并排塔器的风致振动响应实验研究。根据相似理论，对于此类结构风洞实验，需要满足流体力学相似准则、质量阻尼相似以及弹性相似准则，则实验模型和实际结构可认为是运动相似的。本实验结合并排塔器实际操作工况，取来流风速为0.5～17m/s，对应雷诺数范围是1.7×10～2.8×10，处在亚临界区，与塔器的实际工况相同，满足流体力学相似准则。实际钢制塔器属于小质量阻尼体系，NBT 47041—2014《塔式容器》推荐塔器的阻尼比为0.01，本实验模型的阻尼比是0.008，与实际钢制塔器接近，模型质量阻尼比为2.272＜10，属于小质量阻尼体系，实验模型满足质量阻尼相似。实验模型的固有频率是4.67Hz，自振周期是0.214s，与实际塔器的自振周期接近，因此满足弹性相似准则。综上，从结构动力学考虑，可以认为本文有机玻璃材质的实验模型能够反映实际钢制塔器的振动特性。

根据NBT 47041—2014《塔式容器》，在塔器1/3 塔高处安装轴向翅片或螺旋形翅片的扰流器，可减缓或防止塔的共振。然而，对于紧密布置的并排塔器，一方面需要破坏塔器周围的卡门涡街，另一方面需要减小由不规则旋涡引发的附加气动力。为此，本文设计了3种微型翅片，其尺寸参数与轴向翅片相比更小，宽度参数与厚度参数相等，且排布更加紧密，同一圆周上的翅片数为12，相互之间的夹角为30°。相邻圆周上的翅片彼此错开15°。微型翅片的尺寸参数在表2 中列出，其结构形式如图3所示。

表2 微型翅片尺寸参数表

图3 微型翅片结构及安装示意图

将上述模型安装在低湍流度直流式风洞的试验段内，如图4 所示。风洞试验段长宽高为1.1m×0.5m×0.5m，风速范围是0.5～30m/s。通过两个激光位移传感器（KEYENCE IL-600）测量并排塔器模型的横风向位移，采样时间为120s，采样频率为248Hz，采样频率大于20倍的固有频率，符合奈奎斯特采样定理。测点位置位于塔器中央，高度为/2。

图4 实验装置示意图

1.2 实验方案

Fan 等对不同排布形式下柔性多圆柱流致振动的研究结果表明，在串列排布下，多圆柱横风向振动最为剧烈，可以达到顺风向的8～13 倍，因此本文主要研究串列排布下并排塔器横风向激振特性。实验模型排布与测点布置情况如图5所示，为方便下文的计算与分析，定义间距比和折合流速两个参数。

图5 模型排布与测点位置图

（1）间距比间距比定义为相邻两塔器的中心间距与塔器直径之比，符号为/。结合文献[2-3]，本文在不同流动模式对应的间距比范围内均匀选取若干组开展实验，如表3所示。根据标准[27-28]，在实际工况下，塔器间距比/＜2的适用情况较少，故仅取/=1.3为代表进行研究；当2≤/＜5时，并排塔器耦合机制复杂且实际应用情况最多，故在该范围内取5组间距比进行详细研究与分析；当/≥5时，并排塔器耦合作用减弱，故在该范围内取2 组间距比即可确定并排塔器的振动特性。

表3 间距比S/D设置

（2）折合流速折合流速（）是一个流速的量纲为1的参数，用来表征任意结构振动一个周期内流体路径与结构特征尺寸的关系，其表达式为式(3)。

为了研究不同折合流速下并排塔器的振动特性，结合生产实际的风速情况，本文取来流风速为0.5～17m/s，在该范围内结合并排塔器的振动形式较均匀地设置15～20组风速值进行实验，对应的折合流速范围为6～140。

2 并排塔器横风向激振特性分析

2.1 位移时程曲线分析

首先对未安装微型翅片的塔器振动响应进行测量和分析。各振动状态下并排塔器横风向位移响应的时程曲线如图6 所示。图6(a)是间距比/＜2 时的横风向位移时程曲线，由图可知上、下游圆柱可看作单钝体结构，呈现明显的驰振特征，振幅保持稳定。且发生驰振时上、下游圆柱的振动能量存在相互转化的现象，一方振幅的增大会导致另一方振幅的减小。图6(b)是间距比2≤/＜5 时横风向振动的特征时程曲线，此时剪切层自上游圆柱分离，并再附着到下游圆柱上，使上游圆柱的振动被抑制，振幅小于0.1，而下游圆柱的振动被激发，呈现明显的驰振特征。当/≥5时，其特征时程曲线如图6(c)所示，上、下游圆柱均发生旋涡脱落，此时上、下游圆柱不再发生驰振现象，但其位移曲线脉动剧烈。

图6 并排塔器的特征位移时程曲线

2.2 误差分析

本文以并排塔器横风向位移均方根的有效值来表示并排塔器的横风向振幅，并将其量纲为1 化，计算公式见式(4)。

式中，A为并排塔器模型的量纲为1横风向振幅；为并排塔器位移响应的均方根，m。

测量不确定度的含义是指由于测量误差的存在对被测量值不能确认的程度，反过来也表明该结果的可信赖程度，是测量结果质量的指标。不确定度越小，表明结果与被测量的真值愈接近，质量越高，水平越高，其数据可靠性及使用价值越高。测量不确定度评定可以分为A 类评定和B 类评定。A类评定根据随机效应进行评定，并用标准偏差表征；B类评定是按照系统效应进行评定，也用标准偏差表征。

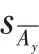
式中，为测量次数，本实验中=3。则有限次测量下，A类不确定度可按式(6)计算。

式中，为与测量次数、置信概率有关的因子。当置信概率=0.68 时，=1.07。根据式(5)、式(6)，计算得出本实验的A 类不确定度=3.14×10（=0.68）。

B 类不确定度可以用仪器的最大允许误差表示，即式(7)。

式中，为包含因子，本实验取=3，激光位移传感器的最大允许误差Δ=50μm，对其进行量纲为1化，得=6.67×10。

根据A类不确定度和B类不确定度，可得到合成标准不确定度[式(8)]。

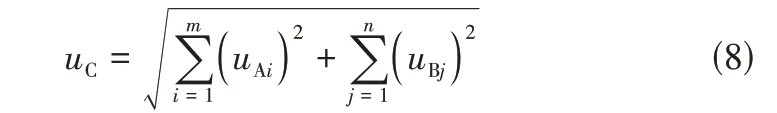
测量结果标准不确定度的相对大小用相对标准不确定度表示，其表达式为式(9)。

根据式(8)、式(9)，得到本实验测量结果的相对标准不确定度(A)=1.23%（=0.68）。

2.3 振幅分析

各间距比下，并排塔器的横风向振动响应如图7、图8所示，三种典型振动模式的特点如下。

（1）单钝体模式其旋涡脱落模式如图7(a)所示，振幅如图8(a)所示，上游圆柱在折合流速=26 时发生类驰振的发散横风向振动，其振幅随折合流速的增加而增大；当折合流速=86时，振动能量由上游圆柱转移到下游圆柱，使得下游圆柱振幅增大，上游圆柱振幅减小；随着折合流速的进一步增大，振动能量又由下游圆柱逐渐转移到上游圆柱，使上游圆柱的最大振幅达到1.31。因此，该范围内并排塔器的横风向振幅较大，上游圆柱呈现发散驰振的特征，在实际工况中最为危险。

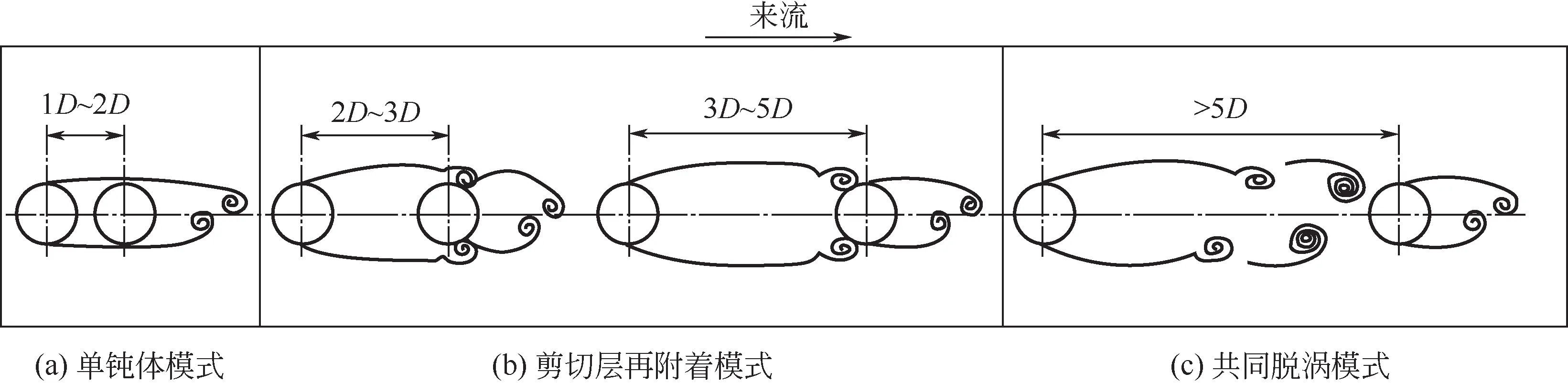
图7 各振动模式下，并排塔器的旋涡脱落模式

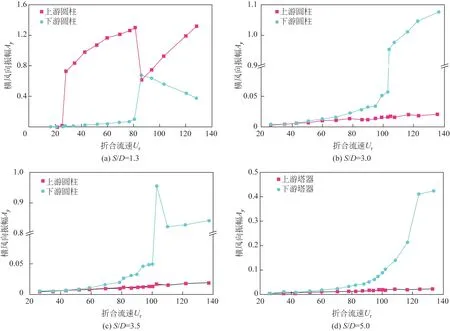
图8 各间距比下并排塔器的振动响应

（2）剪切层再附着模式其旋涡脱落模式如图7(b)所示，振幅如图8(b)、图8(c)所示，并排塔器的振幅随折合流速的增大而增大，上游圆柱的振动明显受到抑制；当折合流速增大至=103 时，下游圆柱发生尾流驰振现象。值得注意的是，当间距比/≤3.0 时，下游圆柱尾流驰振的振幅发散，随折合流速的增大而持续增大，在实验范围内的最大振幅高达1.08，如图8(b)所示；而当/＞3.0 时，下游圆柱发生尾流驰振，其横风向振幅会出现一个峰值，随着折合流速的进一步增大而收敛，稳定后的横风向振幅仅为0.84。在实际工况中，应重点关注下游圆柱的振动。

（3）共同脱涡模式其旋涡脱落模式如图7(c)所示，振幅如图8(d)所示，上、下游圆柱的振幅均随折合流速的增大而增大，当折合流速增大至=124时，并排塔器横风向振幅趋于平稳，且整个过程中没有驰振现象发生。下游圆柱的最大横风向振幅仅为0.42，且随间距比的增大而减小，此时振幅接近单圆柱振幅，按照单塔设计即可。

3 微型翅片的横风向减振特性分析

3.1 安装微型翅片的横风向振幅分析

不同间距比/下各塔横风向振幅随折合流速的变化曲线如图9 所示。当/=1.3 时，随折合流速的增大，安装微型翅片（尺寸A）的上游圆柱横风向振幅先增大后减小；而对于其他尺寸参数的微型翅片，上游圆柱的横风向振动明显受到抑制，当折合流速增大至=87时，上、下游圆柱同时发生类驰振的横风向振动，其振幅显著增大，随后保持稳定，如图9(a)所示。该现象说明当间距比很小时，更微小的翅片结构（尺寸B、尺寸C）能够改善并排塔器的流场，避免上游圆柱在较低的临界风速下即发生发散驰振；且当达到驰振临界风速后，安装微型翅片可使振幅收敛。

当/≥2时，安装微型翅片（尺寸A）的并排塔器的横风向振动明显受到抑制，与其他尺寸参数相比，下游圆柱的振幅显著降低。这说明在该间距比范围内，适当增大微型翅片的厚度及长度参数可以显著改善流场，增强破涡效果，抑制下游圆柱的振动，阻止尾流驰振现象的发生。值得注意的是，根据图9(b)、图9(c)，当2≤/＜5时，微型翅片（尺寸B）的减振效果优于微型翅片（尺寸C），这说明在该间距比范围内，并排塔器之间相距较近，此时增大微型翅片的厚度参数可以增强破涡效果，减小尾流对下游塔器的能量激励，获得更好的减振效果。

图9 不同间距比下，安装微型翅片的并排塔器的振动响应

当/≥5 时，微型翅片（尺寸C）的减振效果优于微型翅片（尺寸B），如图9(d)所示。这说明在该间距比范围内，各座塔器之间相距较远，此时尾流流经下游圆柱时大部分能量已经衰减，翅片的厚度不再是主要的影响参数。而翅片的长度，即翅片的覆盖率越大可使减振效果更加明显。

3.2 微型翅片的减振性能分析

上、下游圆柱最大振幅随间距比的变化如图10所示。根据图10(a)，当间距比/≥2.0时，上游圆柱的最大横风向振幅显著降低，且与单圆柱振幅（0.027）十分接近。当间距比/=1.3时，微型翅片（尺寸A）可使上游圆柱振幅减小69.47%；微型翅片（尺寸B、尺寸C）可使上游圆柱振幅减小78.63%。根据图10(b)，在/=1.3时，三种微型翅片对下游圆柱的减振性能接近，约为35%；当2≤/≤8 时，微型翅片（尺寸A）的减振效果显著，可使上游圆柱的振幅降低86.46%～95.67%。然而对于微型翅片（尺寸B、尺寸C），尽管其可以在一定程度上降低并排塔器的振幅（5.89%～64.68%），但是模型的振动特性仍与光滑圆柱相似，上、下游圆柱依旧会发生驰振现象。这说明微型翅片的减振性能对其尺寸参数十分敏感，根据本文的实验结果，在2≤/≤8时推荐微型翅片的厚度≥0.1，微型翅片的长度≥0.9，微型翅片的覆盖率不小于30%。

图10 各实验模型的最大横风向振幅随间距比变化曲线

本文的实验模型满足相似理论，与工业尺度塔器是运动相似的，实验结果可以指导工程设计。此外，本文所设计微型翅片的各尺寸参数均以量纲为1形式表示，与行业标准《塔式容器》（NB/T 47041—2014）中的量纲为1方法相同。因此，在工业尺度实验装置中，只需按照实际尺寸进行调整，即可实现大型试验装置的应用。