并排塔器耦合流场特性研究
2019-05-13王中辰曾万川2娟3樊显涛
谭 蔚,王中辰,曾万川2,卢 娟3,樊显涛
(1.天津大学,天津 300350;2.昆明有色冶金设计研究院股份公司,昆明 650051;3.全国锅炉压力容器标准化技术委员会,北京 100029)
0 引言
塔器是化工操作单元中的重要设备,在化工装置中投资比例高达25%~46%[1]。如今塔器不断地向高参数和大型化方向发展,布置也愈加密集,其中固定在同一基础上,相互之间距离较小且按顺序排成一行的塔器被称为并排塔器。由于并排塔器存在耦合振动,因此现行对于单塔的设计标准并不适用于并排塔器的设计。因此,对并排塔器的耦合流场特性进行研究,以期为并排塔器的设计提供依据,具有较大的工程意义。
并排塔器风致振动的本质是多圆柱的绕流问题。圆柱绕流问题一直受到国内外学者的广泛关注。贾晓荷[2]对多圆柱绕流的流场特性和尾流特征进行了较详细的总结。及春宁等[3-4]采用浸入边界法对雷诺数Re=100下串列双圆柱的流致振动进行数值模拟,研究结果表明,在不同间距比下,双圆柱的振动响应和柱间流态不同。Assi等[5-6]对Re在100~200范围内的串列双圆柱尾流激振的机理展开了深入的试验研究,发现下游圆柱的大幅振动是受到上游圆柱尾涡的影响,并据此提出了多圆柱尾流激振机理。对于露天放置的塔器,在风载荷作用下会发生横风向振动和顺风向振动,其Re通常处于亚临界区(300 本文采用ANSYS CFX数值模拟,对亚临界区和过渡区雷诺数下并排塔器的耦合流场特性开展三维稳态和瞬态数值模拟研究,旨在为并排塔器的设计与振动分析提供参考。 本文忽略并排塔器的操作平台及裙座,结构简图及建立的几何模型如图1所示。 (a)结构简图 (b)几何模型 图1 并排塔器结构简图及几何模型 大量研究结果表明[10],在并列及交错排布下,多圆柱仅在间距比为2及以下时存在强耦合区,且各圆柱的边界层相互抑制,振幅相对较小;而在串列排布情况下,由于尾涡激振,多圆柱的振幅远大于单圆柱,因此本文主要研究串列排布情况下并排塔器的耦合流场特性。以某座并排塔器为例,其参数如表1所示。 为方便下文的计算与分析,定义间距比和约化速度两个参数。 表1 计算模型参数 (1)间距比。 间距比S/D定义为相邻两塔器的中心间距S与塔器直径D之比。根据HG/T 20546—2009《化工装置设备布置设计规定》及SH 3011—2011《石油化工工艺装置布置设计规范》中的相关规定[11-12],并结合工程实际,本文研究中选取间距比S/D分别为2,3,4,5。 (2)约化速度。 约化速度U是一个流速的无量纲参数,用来表征任意结构振动一个周期内流体路径与结构特征尺寸的关系,其表达式为: U=v/Df (1) 式中v——实际风速,m/s; D——塔器直径, m; f——塔器固有频率,Hz。 根据并排塔器的实际工作条件,查询风力等级表得到实际风速的取值范围为0~10.8 m/s,在该范围内将实际风速均匀分为6组,代入式(1)中计算约化速度并取整,得到约化速度U的值为2,7,12,17,22,27。 在计算域中建立串列三圆柱模型,将流体域划分为不同的区域,进行网格划分,在靠近圆柱的区域进行局部网格加密,如图2所示。在不同间距比下得到网格数和节点数为4.7×106~7.5×106不等。网格质量及偏度如表2所示,网格质量集中在0.9~1.0之间,网格偏度小于0.05,网格的质量较高。 (a)计算区域划分 (b)圆柱周围网格加密 图2 网格划分 表2 网格质量及偏度 本文应用k-ε模型进行三维稳态流场数值模拟,采用大涡模拟(LES)方法进行三维瞬态流场数值模拟。大涡模拟是通过滤波函数将大尺度涡和小尺度涡分离开,对大尺度涡用N-S方程直接计算,对于小尺度涡则用适合的湍流模型来近似。大涡模拟在计算并排塔器风场时,既可以准确地获得尾涡的细微结构及流动图像;又减少了因较多的网格数目引起的庞大计算量。 对边界条件的设置如下。 (1)入口:入口风速的设置依据标准NB/T 47041—2014《塔式容器》[13],风速沿高度变化呈指数规律,取粗糙度为B类。风速分布公式为: (2) (2)出口:出口压力边界,P=0 Pa。 (3)两侧及顶面:对称边界。 (4)圆柱表面及底面:无滑移的壁面边界。 在计算过程中,时间步长取Δt=0.01 s。 塔器发生横风向和顺风向振动是由于表面受到波动的风载荷作用。为了分析并排塔器表面风压的分布,本文计算了压力系数,其表达式为: (3) 式中Cp——压力系数; p——塔器表面静压力,Pa; p∞——大气压力,Pa; ρ——空气密度,kg/m3。 不同间距比S/D下,各塔器的压力系数曲线如图3所示。 (a)S/D=2 (b)S/D=3 (c)S/D=4 (d)S/D=5 从图3可以看出,当间距比S/D一定时,不同约化速度下各曲线的形状几乎相同,这是由于当雷诺数处于亚临界和过渡区时,风的流动均为湍流流动,这种不规律的流动形式在并排塔器表面造成的压力分布形式相同。因此,本文选取S/D=5,U=2时,各塔器的压力曲线,同时结合单塔的稳态模拟结果进行分析,如图4所示。可以看出,上游塔器1的压力系数波动与单塔相比更为剧烈,而中游塔器2和下游塔器3的压力系数则相对平稳,曲线形状更为平缓,这是由于下游两座塔器处在背风侧,上游塔器起到了遮挡及稳流的作用。 图4 并排塔器的压力系数曲线(S/D=5,U=2) 上游塔器1、中游塔器2和下游塔器3在各间距比S/D下的压力系数曲线如图5所示。 (a)上游塔器1 (b)中游塔器2 (c)下游塔器3 对于上游塔器1,各压力系数曲线的形状十分相似,说明位于背风侧的下游塔器对上游塔器的影响较小,流场的耦合作用较弱;对于中游塔器2和下游塔器3,随S/D增大,压力系数曲线的波动愈加剧烈。中游塔器2的压力系数曲线在S/D由4至5时的平均偏差值为34.6%,而下游塔器3仅为15.0%,因此中游塔器流场的耦合作用最强,下游塔器流场的耦合作用相对较弱。当S/D增大到5后,流场的耦合作用减弱。 表3 分离点位置 (a)上游塔器1 (b)中游塔器2 (c)下游塔器3 图6 分离点位置示意 分离点表征了圆柱表面边界层分离的位置,反映了多圆柱耦合的影响效果。表3和图6给出了不同间距比S/D下各塔器的分离点出现的位置。结果表明,各塔器分离点出现的位置基本对称。与上游塔器1相比,中游塔器2和下游塔器3的分离点明显后移,由此造成中游及下游塔器的表面压力分布更加平缓,与图5的曲线规律相吻合。 升力系数是一个无量纲数,其表达式为: (4) 式中CL——升力系数; FL——升力,N; A——沿风向的投影面积,m2。 不同S/D下各塔升力系数的均方根随约化速度的变化曲线如图7所示。可以看出,各塔的升力系数均大于标准中的推荐值0.5[13],表明并排塔器在横风力的作用下振动幅度较大。当S/D=2和S/D=5时曲线相对平稳;当3≤S/D≤4时各塔器的曲线波动较大,说明3≤S/D≤4的范围是强耦合区;当S/D=5时,上游塔器升力系数的均方根与标准中的推荐值0.5比较接近,说明在间距比S/D=5时,下游塔器对上游塔器存在稳流作用,使上游流场的耦合作用减弱。因此,在并排塔器设计时,推荐间距比S/D>5。 (a)S/D=2 (b)S/D=3 与升力系数相似,阻力系数的表达式为: (5) 式中CD——阻力系数; FD——阻力,N。 不同S/D下各塔阻力系数的均方根随约化速度的变化曲线见图8。可以看出,在亚临界区雷诺 数下,并排塔器的阻力系数随约化速度的增大骤然下降;在过渡区雷诺数下,曲线相对平稳。当2≤S/D≤4时,上游塔器对位于下游的塔器存在遮挡作用,使得上游塔器的阻力系数明显大于中游塔器和下游塔器。同时,由于尾涡的能量输入,下游塔器的阻力系数大于中游塔器。当S/D=5时,各塔的阻力系数近似相等,可视作单座塔器。 (a)S/D=2 (b)S/D=3 (c)S/D=4 (d)S/D=5 图8 不同间距比下,阻力系数均方根随约化速度的变化曲线 斯托罗哈数是非定常流场中涡脱频率的量度,与塔器发生横风向共振的临界流速密切相关[14-15],本文对升力系数进行快速傅里叶变换,计算了斯托罗哈数St。不同S/D下St随约化速度U的变化见表4。可以看出,当S/D=2时,St在0.2附近波动,这是由于各塔间距较近,各塔之间并未形成完整的旋涡,仅在下游塔器3的尾流区形成一个稳定的卡曼涡街区域,此时可将3座塔器近似视为一个整体。当3≤S/D≤5时,亚临界区内St在0.2附近波动,且大部分高于0.2;其中过渡区内St在S/D=4时均明显高于0.2。整体而言,St分布规律性差,波动大,由此可见,在3≤S/D≤5范围内,各塔之间耦合作用强烈,流场更加复杂。与单塔相比较,St变大会导致并排塔器发生横风向共振的临界风速变小,使其在较低的风速下发生共振,在工程设计时应重点关注。 表4 不同间距比下,斯托罗哈数St随约化速度的变化 本文采用ANSYS CFX数值模拟,分别开展了并排塔器三维稳态和瞬态流场研究,计算并分析了并排塔器的流场特性。通过计算与分析,得到如下结论。 (1)上游塔器的压力波动比单座塔器更加强烈,中游塔器和下游塔器的压力波动则相对平缓;处在流场中不同位置的塔器的耦合作用强弱顺序为:中游塔器>下游塔器>上游塔器。当S/D=5时,耦合作用几乎消失。 (2)各塔器两分离点的位置基本对称。与上游塔器相比,下游两座塔器的分离点明显后移,导致其表面压力分布波动较小。 (3)在3≤S/D≤5时,斯托罗哈数的波动会导致临界风速变小,使并排塔器在较低的风速下即发生共振。 (4)3≤S/D≤5范围是一个强耦合区域,S/D>5时,耦合作用减弱,推荐在并排塔器设计时,S/D>5。1 并排塔器数值模型建立
1.1 几何模型

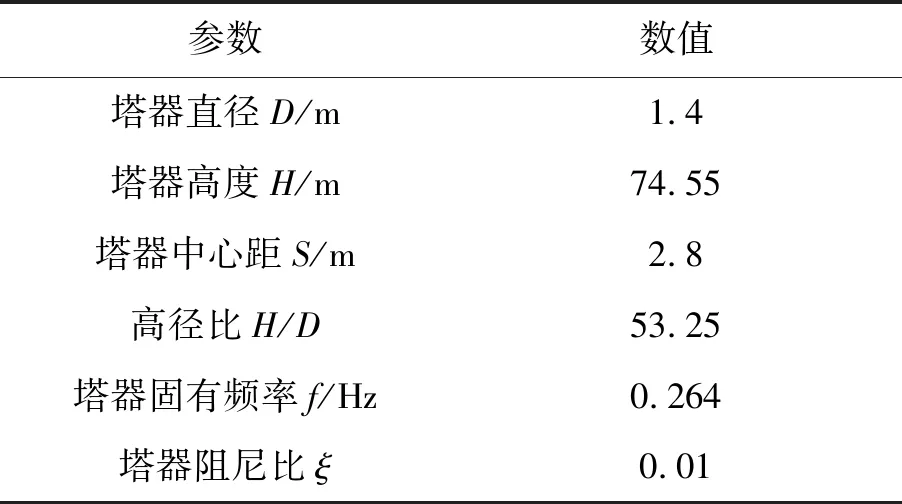
1.2 数值计算模型


1.3 模拟方法与边界条件
2 三维稳态数值计算结果分析
2.1 并排塔器表面压力分布

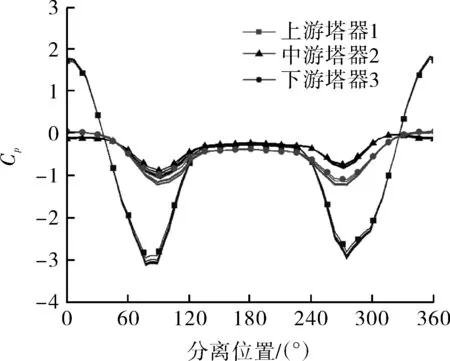

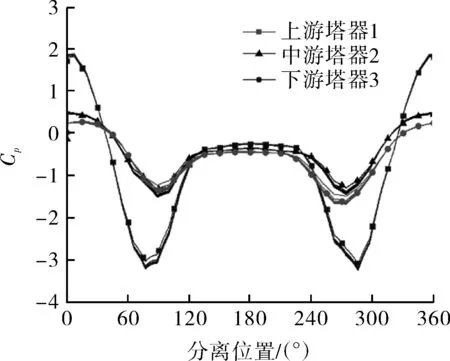

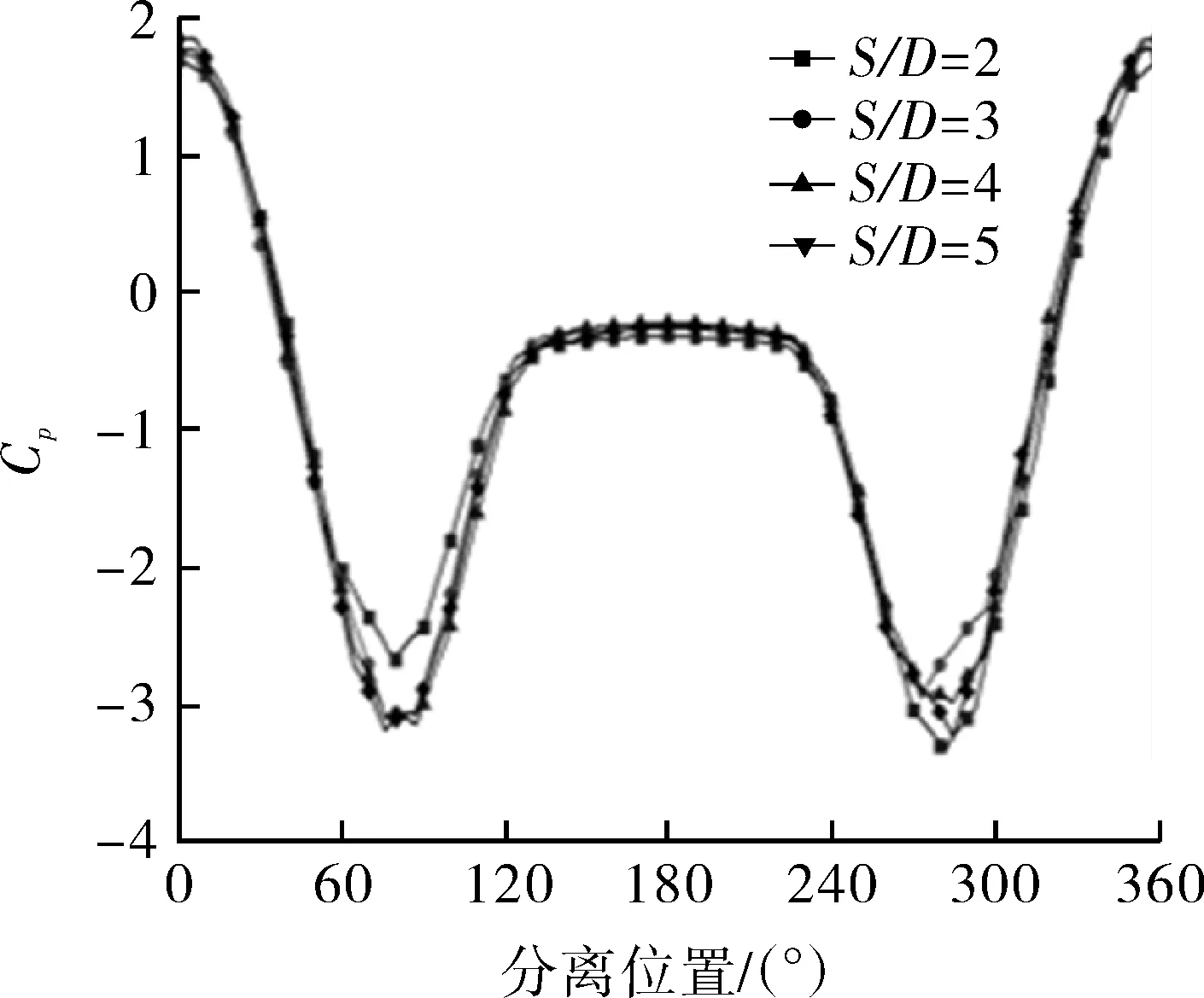


2.2 边界层分离点特征分析


3 三维瞬态数值计算结果分析
3.1 升力系数的计算与分析


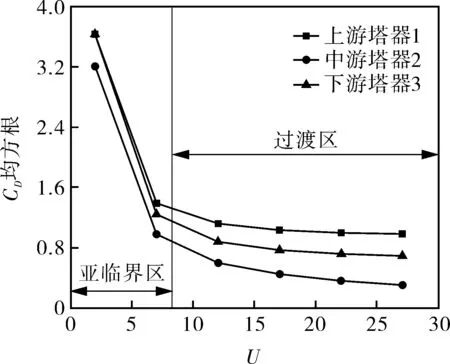
3.2 阻力系数的计算与分析

3.3 斯托罗哈数St的计算及分析

4 结论
