脱碳塔风载荷下非正常振动的分析
2023-02-18娄庆祥董有智潘建华
娄庆祥,董有智,潘建华
(1.合肥工业大学 机械工程学院,合肥 230009;2.国家管网集团 东部原油储运有限公司,江苏 徐州 221000;3.合肥工业大学 工业与装备技术研究院,合肥 230009)
0 引言
石油化工已经成为国民经济的支柱性产业, 随着国内对石油的消耗量日益增加,化工厂的规模也不断扩大,塔器广泛应用于石油化工、炼油、污水处理及医药等产业,是最重要的生产设备之一。塔器的投资巨大,其安全可靠性直接关系到整个生产装置的产能、质量、能耗及生产成本,而且也直接关系到现场人员的人身安全[1]。
塔器是典型的高耸设备,近年来塔器开始呈现高度高、直径小和质量大的趋势,大高径比塔器数量逐年增多。大高径比的塔器具有柔性大的特点,因此对风载荷较为敏感。近年来,高耸塔器因发生非正常晃动而破坏的例子不胜枚举[1-6]。在塔器正常操作状态下,由于塔体内部有介质存在,阻尼比较大,不易发生风致振动。但是当塔器处于空塔或者停车状态时,阻尼比较小,极易发生风致振动[7]。塔器振动问题一直困扰着设计者,目前主要通过增大自振周期和增大阻尼比的防振方法[8-9]。文献[10]指出在计算塔器动挠度时阻尼比取值最好来自现场实测,或者根据相似理论建立实验模型。文献[11]在对高耸钢烟囱的抗风研究中指出现阶段各标准对高耸钢结构的阻尼比取值偏大。文献[12]在对高耸塔器风致振动的现场实测与疲劳分析中指出,塔器检修时的阻尼比小于设计计算时的阻尼比。文献[13]也指出塔器阻尼比取值给设计者造成极大的困扰。
1 塔器振动情况及主要参数简介
此次发生非正常振动的塔器为某石化公司的脱碳塔,脱碳塔在停车期间后多次在5级风力的作用下发生剧烈晃动,而且晃动具有一定的周期性。此脱碳塔高为57.8 m,塔筒内径为2 m,高径比较大,属于高柔结构。设计的基本风压为450 N/m2,设计使用年限为15 a,但是在安装完成1 a后发生了较大幅度的非正常振动。
塔器的主要参数如表1所示。
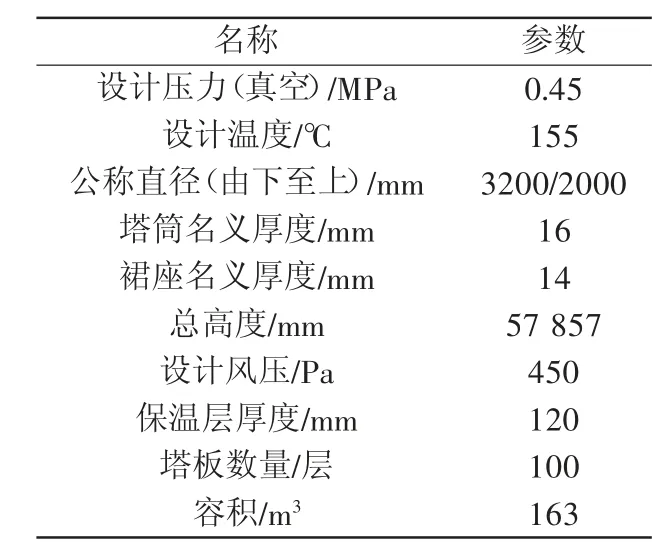
表1 主要设计参数
塔器在非工作期间下发生剧烈晃动,并且几次发生大幅振动时当天的风速并不高,工作人员拍下了其中一次塔器晃动的视频及多张照片,通过对比图像中不同时刻塔身上特定点在坐标格栅中位置差异的方法,进行塔器塔顶晃动幅度的测算。通过测算此塔最上层的平台外缘点W1的最大偏移量为1.18 m,折合成塔的挠度为0.590 m。查询塔器发生大幅度非正常振动时的气象条件,发生振动时当地的极大风速为7.3~8.3 m/s,并伴有微量降雨。
塔器振幅测量过程,取3个测量点W1、W2、W3,以照片左上角为坐标系原点,考虑远近视角对测量的影响。以直径2 m为参照距离,点W1、W2、W3对应的每个像素坐标的实际距离分别为2/22 m、2/23 m、2/25 m。

图1 塔器振幅测算图(右二塔)
W1处对应的最大位移为13×直径÷22=1.18 m,W2处对应的最大位移为13×直径÷23=1.13 m,W3处对应的最大位移为12×直径÷25=0.96 m,所以可得塔顶最大振幅为0.590 m。
2 塔器振动计算
塔器在风载荷的作用下会发生2个方向的振动:振动方向与风向相同的顺风向振动,以及振动方向与风向垂直的风诱导振动。
2.1 塔器的顺风向塔顶挠度计算
运用风载荷作用下的等直径等壁厚的塔器顶部挠度公式进行计算[14],公式如下:

图2 测量点偏移距离

表2 塔器风致振动位移测量值

式中:ft为塔顶风压高度变化系数,取ft=1.74857;K1为体形系数,取K1=0.7;P0为塔器离地10 m高度处单位长度风载荷,N/mm;PD为塔器顶部单位长度风载荷,N/mm。
计算结果如表3所示。

表3 塔器顶部顺风向挠度
由计算结果可知,在基本风压与实际风压下塔顶部顺风向最大挠度都远远小于塔顶实际发生振动的幅度。
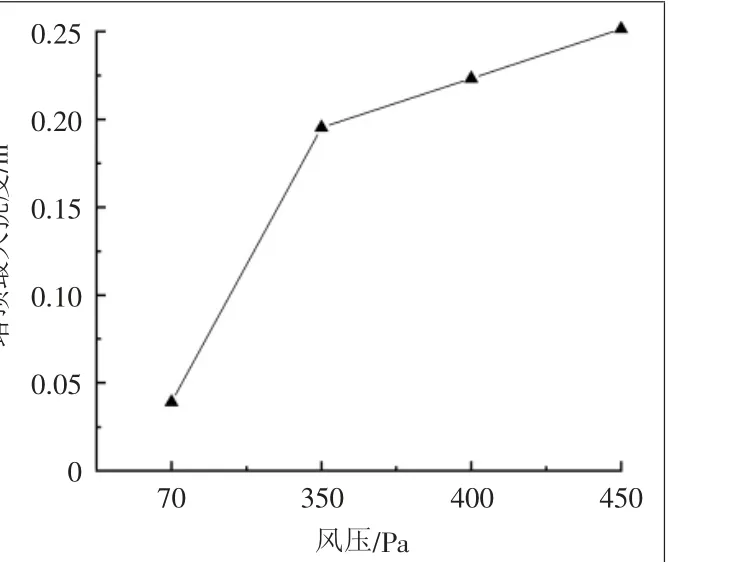
图3 塔器顶部顺风向挠度数值
2.2 塔器的横风向塔顶振幅计算
在塔器直径和高度一定的情况下,当外界风速达到一定的范围时,绕流过塔器的空气会在塔器的背风面两侧产生分离,交替分离的空气会形成漩涡,漩涡以一定的频率从塔体背风面交替脱落,形成卡门涡街。交替脱落的漩涡,使得塔器两侧流体压强也周期性变化,从而对塔体产生了一个垂直于风向且方向周期性变化的激振力,使塔器发生横风向的周期性晃动。当激振力的周期与塔器的自振周期接近时,塔器就会发生风诱导共振。风诱导共振时振幅会骤然增大,严重时会使塔器发生损坏。
首先,通过计算临界风速判断共振是否发生,第j振型共振临界风速及结构顶部风速可由下式计算[14]:
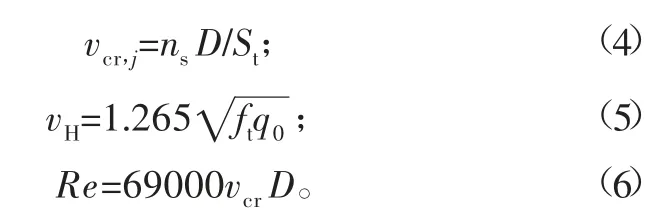
式中:ft为塔器顶端处风压高度变化系数,取ft=1.7486;St为斯特罗哈数,取St=0.2;q0为基本风压值;vcr,j为第j阶临界共振风速,m/s;D为塔器外径;ns为塔器的自振频率;vH为结构顶部风速;vcr为设计风速,取vcr=vH。计算结果如表4所示。

表4 塔器临界风速及顶部风速计算结果
根据JB/T 4710-2014 标准中横风向共振的判定条件,vcr大于第一振型与第二振型的临界风速,应考虑第一振型和第二振型的振动。
接下来计算前两阶的横风向塔顶振幅。
横风向塔顶振幅计算公式[14]为
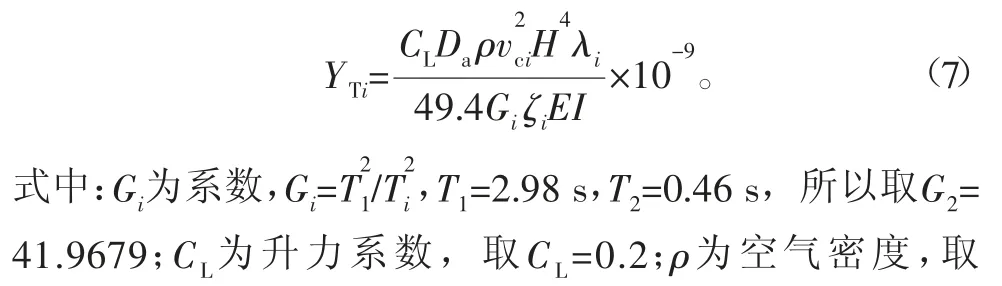

当第一振型临界风速取为实际振动发生时的风速8.1 m/s(换算到塔顶风速为10.62 m/s),阻尼比ζ分别取0.01、0.03/(2π)、0.02/(2π),计算结果如表6所示。

表5 前两阶临界风速下塔器的横风向顶部振幅

表6 实际风速下塔器的横风向顶部振幅
3 计算结果分析
通过计算可知,塔器顺风向的顶部挠度小于塔器发生晃动幅度,无论是设计风压下还是发生晃动的实际风压下的顶部挠度计算值都很小,符合中国规范的要求,因此可以判断顺风向风载荷不是造成晃动的主要原因。
对塔器的横风向共振进行分析,通过计算临界风速可以判断塔器有可能发生前两阶共振,取阻尼比为JB/T 4710-2014标准推荐值时,一阶临界风速和二阶临界风速下的横风向共振振幅均小于实际振幅,当阻尼比取JB/T 4710-2014标准中比较保守的文献推荐值时,即取为空塔阻尼比推荐值时,一阶临界风速下横风向共振的塔顶振幅超过实际振幅,从计算结果可以看出阻尼比的取值大小对横风向塔顶振幅的影响很大。
由于塔器发生振动时的风速为10.62 m/s,稍大于一阶共振风速,因此将一阶共振风速替换为实际风速进行计算,当阻尼比取为空塔阻尼比推荐值0.003 18时,第一振型振幅计算值为0.519 8 m,振幅与塔器振动视频图像处理结果接近。可推测塔器发生振动时的阻尼比大小即为较为保守的空塔阻尼比的推荐值,也可以看出阻尼比取值的正确与否关系到能否准确预测塔器的振动幅度,因此对阻尼比取值进行探讨是十分有必要的。
4 阻尼比计算方法的对比
阻尼比是线性黏性阻尼系数与临界阻尼系数之比。线性黏性阻尼系数是线性黏性阻尼力与变形速度的比值,临界阻尼系数是使偏离平衡位置的单自由度系统无振动回到平衡位置的最小黏性阻尼系数。
目前,很多学者用对数衰减率与阻尼比来表征化工塔器的阻尼。如图4所示,当结构的振动是理想状态下的单一频率振动时,对数衰减率δ是1个周期内2个同向相邻振幅yi与yi+1之比的自然对数,衰减率的计算公式为

图4 有阻尼结构的振幅衰减曲线

求出对数衰减率以后。将对数衰减率除以2π可以得到阻尼比。如果运用式(8)计算对数衰减率,需要通过实验测出振幅的衰减。在实际使用中会受到诸多限制:首先,其振动信号必须是单频振动;其次,其振动波形是自由衰减振动波形,测定条件较为苛刻,难以达到如此理想的条件。因此,人们经常根据相似原则选择与设计塔器尺寸相似塔器的阻尼比。此外,日本、美国及中国的相关标准也总结大量经验与数据,对塔器阻尼比的取值做了相应规定[14-20]。表7中列举各标准对阻尼比的取值。

表7 不同标准的阻尼比数值
从表7中可知,多数规范中直接给出了阻尼比的取值,或者指定一个阻尼比的取值范围,但都建议进行实测,或者参考文献中尺寸相近塔器的实测值,目前为止尚无可靠的塔器阻尼比计算公式。在计算塔的动挠度时,阻尼比的值最好来自对该塔进行现场实测的数据或者根据相似论的基本原理进行模型试验取得的结果[14,21]。美国ASME STS-1-2016规范与欧洲BS EN 1991-1-4:2005规范给出了较为详细的阻尼比计算方法,文献[22]也通过大量实验拟合出阻尼比经验公式。
4.1 美国ASME标准阻尼比计算方法
美国ASME标准[15]对脱碳塔阻尼比进行计算,计算过程如下。
根据脱碳塔的尺寸结构选取结构阻尼比ζs为0.002,动力阻尼比ζa按照式(9)进行计算:

式中:Cf为升力系数,根据表7确定,取Cf=0.7;ρ为空气密度,取为ρ=0.07799 lbm/ft3;D为塔体平均直径,取D=6.61417 ft;V为风速,取共振发生时的速度V=33.4642 ft/s;ma为距塔顶1/3处的单位长度质量,取ma=534.5977 lb/ft;f1为塔器的一阶共振频率,取f1=0.3356 Hz。

表8 升力系数Cf值
将上述值代入式(9)可得ζa=0.00536,所以塔器的阻尼比ζ=ζs+ζa=0.002+0.00536=0.00736。
4.2 欧洲规范阻尼比计算方法
欧洲规范[16]中可使用式(10)估算出基本弯曲振型的阻尼对数衰减率δ:

式中:δs为结构阻尼的对数衰减,取δs=0.012;δa为基本振型的气动阻尼的对数衰减;δd为特殊装置(调谐质量阻尼器、晃动罐等)引起的阻尼对数衰减,本算例中无特殊装置。
气动阻尼的对数衰减δa可由下式计算[16]:

式中:cf为升力系数,取cf=0.2;ρ为空气密度,取ρ=1.25 kg/m3;b为结构外径,取b=2.272 m;vm为平均风速,取vm(z)=37.9066 m/s;n1为结构一阶振动频率,取n1=0.3356;me结构单位长度等效质量,取me=994.5511 kg/m。
代入数据可得δa=0.0323,对数衰减率δ=δa+δs+δd=0.012+0.0323+0=0.0443,可得阻尼比ζ=δ/(2π)=0.0443/(2π)=0.00705。
4.3 国内学者阻尼比经验公式
李蓉[22]进行了大量实验,通过测量多组单塔模型的衰减率,进而计算出多组单塔模型的阻尼比,使用这些阻尼比与单塔模型的结构尺寸参数进行无因次法与最小二乘法的拟合,得出计算塔器一阶阻尼比的经验公式。该公式把塔器的材料及塔器结构参数考虑在内,材料数据有密度ρ和质量M,结构参数有壁厚t、高度H及外径D,该公式考虑的因素较多,有一定的参考价值。下面主要介绍李蓉提出的经验公式:

式中:H为塔器高度,取H=57.857 m;ρ为材料密度,取ρ=7850 kg/m3;D为结构外径,取D=2.032 m;t为塔壁厚度,取t=0.016 m;M为塔器质量,取M=108408.29 kg。代入数据可得ζ=0.5322。
4.4 计算结果分析
将各规范的阻尼比推荐值与塔器发生共振时的阻尼比ζ=0.01/(2π)进行比较,比较结果及在各阻尼比取值下的一阶横风向塔顶振幅如表9所示。

表9 阻尼比规范值与实际值比较
从图5结果可以看出,不同标准阻尼比取值下横风向振幅差异较大。从表9中结果可知,对于本文中的塔器,上述规范中的阻尼比计算值都比实际值偏大,其中欧洲规范误差最小为121.70%。中国石油化工塔型设备设计基础规范的误差最大高达1000.63%。文献[22]中提出的经验公式不太符合本文中塔器的实际情况,误差较大。

图5 不同标准阻尼比取值下的横风向振幅
5 结语
塔器发生横风向共振的危害比顺风向振动的危害大得多,塔器横风向共振问题需要引起重视,其中空塔更容易发生风诱导共振,风诱导共振在塔器停车检修期间也时有发生。因此在设计大高径比塔器时一定要考虑横风向的共振问题,对于安装完成塔器的防振问题也必须给予足够的重视。
1)高耸塔器要严格按照JB/T 4710-2014《钢制塔式容器》标准进行横风向风振计算。实例中的塔器按照规范计算符合安全要求,但是塔器却在安装完成后的非工作期间发生较大幅度的横风向振动,可见在塔器安装完成后采取一定的减震措施对塔器的安全运行是十分必要的。
2)根据不同标准对脱碳塔阻尼比的计算结果可知,不同标准的计算方法得到的阻尼比并不相同,其相对误差非常大。脱碳塔计算横风向共振时阻尼比取ζ=0.02/(2π)得出的共振振幅与现场实际振幅接近,为了使塔器能够安全运行,在设计阶段风振计算可以选择JB/T 4710-2014《钢制塔式容器》中提到的空塔阻尼比推荐值进行验证。
3)阻尼比对塔器的横风向共振影响很大。大多数设计规范只是笼统地给出一个阻尼比的取值范围,到目前为止,尚无合适的计算公式来确定塔器的阻尼比,阻尼比取值是一个相当复杂的问题,需要提出更贴合实际情况的塔器阻尼比计算公式。
