用于飞轮储能系统的轴向分相电机的电磁分析与优化设计

朱志莹，朱海浪，邵淋晶，李鑫雅，郭 杰

(1. 南京工程学院 电力工程学院，南京 211167；2. 东南大学 电气工程学院，南京 210096)

0 引 言

飞轮储能系统(Flywheel Energy Storage System, FESS)是一种高功率密度的机械储能系统，具备比能量高、比功率大、体积小、寿命长、充放电快、清洁无污染等优点，在航空航天、交通运输和风力发电等领域获得广泛运用，但其存在的高速运行和悬浮支撑等技术问题极大地限制了它的进一步发展[1-3]。磁轴承支承可降低飞轮储能损耗，但系统结构复杂、临界转速受限且故障率高[4]。近年来兴起的无轴承电机结合磁轴承与电机的双重优点，可简化系统结构，提高临界转速与可靠性，在飞轮储能领域具备独特优势。

无轴承开关磁阻电机(Bearingless Switched Reluctance Machine, BSRM)是一种将传统的开关磁阻电机(Switched Reluctance Machine, SRM)与磁轴承(Magnetic Bearing, MB)相结合的新型电机，其具有结构紧凑坚固、高速高精、无摩擦磨损等优点，将其引入FESS形成磁悬浮飞轮电机(Bearingless Flywheel Machine, BFM)，可简化FESS结构，提高临界转速，并减少运行损耗。但传统BFM所固有的多变量、非线性和强耦合的电磁特性，使其实际控制难度大、运行稳定性低[5]。

为此，文献[6]提出一种新型轴向分相磁悬浮飞轮电机(Axial Split-phase BFM, ASP-BFM)，该电机采用内定子外转子12/12极结构，沿轴向分为两相，每相定子极由4个悬浮极(宽齿)和8个转矩极(窄齿)构成，两者间装有隔磁环，从结构上实现悬浮力与转矩的解耦，可简化FESS结构，提高临界转速，降低飞轮损耗。为了提高ASP-BFM的性能，有必要对其结构参数进行优化以获取更大的转矩和悬浮力[7]。然而，为了避免悬浮力与转矩间的强耦合，APM-BFM采用了上述特殊结构，电机的复杂结构导致需要优化的结构参数增加，对设计速度和精度要求更高[8]。

各种优化算法已经被应用到电机的设计优化，如人工神经网络、和声混沌、果蝇算法、遗传算法和禁忌搜索等。人工神经网络在小样本优化时误差很大[9]；和声混沌算法关键参数的选取缺乏理论基础，相应取值具有主观性[10]；果蝇算法处理高维非线性函数不容易取得全局最优解和局部最优解[11]；遗传算法易早熟收敛，其稳定性差，且处理规模小[12]；禁忌搜索算法在条件判断方面不够成熟[13]。

针对上述问题，本文提出一种基于粒子群算法(Particle Swarm Optimization, PSO)的ASP-BFM多目标结构参数优化设计方法。以一种新型ASP-BFM为研究对象，在电机初始参数的基础上，采用敏感度分析(Sensitivity Analysis, SA)选取电机的关键结构参数，基于有限元仿真(Finite Element Analysis, FEA)得到相应的输出变量组成数据集，利用具有精度高、速度快等优点的极限学习机(Extreme Learning Machine, ELM)算法对数据进行回归训练，得到相应的优化模型，并采取权重惯性调整的PSO对优化模型进行全局寻优，实现电机结构参数的多目标协同优化。最后，利用有限元仿真对比优化前后的结果验证优化结果的有效性。

1 ASP-BFM工作原理

图1为一种新型ASP-BFM的初始结构示意图。该电机沿轴向按相数(A相和B相)分为两段，两相转子极极轴线相差15°，中间装有轴向充磁的永磁体，每相均采用内定子外转子12/12极结构，内定子12极由4个宽齿悬浮极和8个窄齿转矩极组成，其中转矩极极弧为15°，悬浮极极弧为30°，使转子转动过程中转矩极与悬浮极的对齐极弧始终为15°，保证电机悬浮出力的稳定性并提高电磁转矩。每一极定子上叠绕一套控制绕组，每相8个转矩绕组串联，径向相对的2个悬浮绕组串联，两相定子之间的永磁体在径向上为四自由度悬浮力的产生提供偏置磁通；并且，转矩铁心与悬浮铁心之间设有隔磁环，从结构上削弱了转矩与悬浮力的耦合作用。

电机的悬浮极绕组产生磁链ψsa，转矩极绕组产生磁链ψma，其磁路如图2所示。由于转矩极与悬浮极间存在隔磁环，使转矩磁路与悬浮磁路相互分离，从而实现悬浮力与转矩的解耦。

2 ASP-BFM参数敏感度分析

2.1 建立有限元仿真模型

本文运用有限元分析方法建立电机初始仿真模型，其初始结构参数如表1所示。依据二维有限元瞬态场仿真进行分析，设置外电路额定电压为220 V、角度位置控制，经过仿真确定转矩绕组电流ima=4.7 A；利用Matlab/Simulink搭建转子悬浮PID控制系统，在转子重力为9.6 N的情况下，转子发生偏心时悬浮力数值区间为[-20 N，40 N]。选取最大悬浮力对应的悬浮绕组电流为isa=1.88 A。

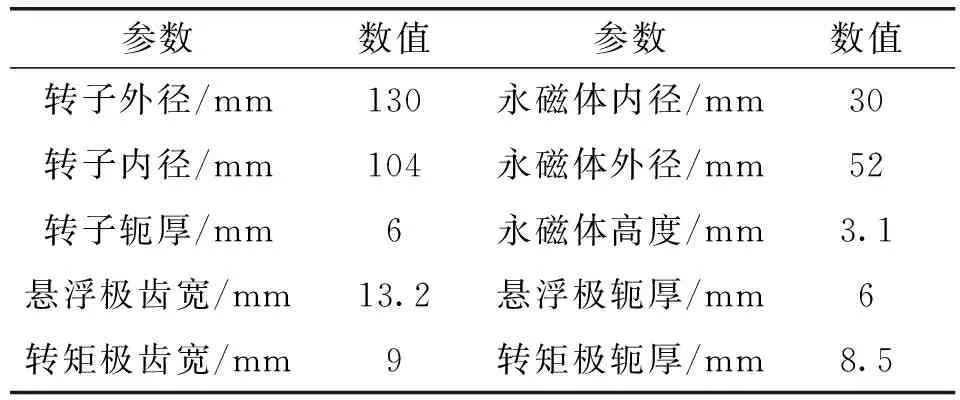
表1 ASP-BFM的初始结构参数

2.2 悬浮力、转矩与结构参数敏感度分析

以ima=4.7 A、isa=1.88 A设置有限元仿真中电机各绕组激励，并以平均悬浮力Favg与平均转矩Tavg两个关键性能指标为例，分析各结构参数变化时的影响，总结得出敏感性参数。图3、图4、图5和图6分别给出了平均悬浮力Favg、平均转矩Tavg与永磁体、转子、悬浮极、转矩极结构参数之间的关系曲线。如图3(a)、图3(c)所示，平均悬浮力Favg随永磁体外径及厚度的增加呈上升趋势。由于永磁体外径和厚度的增加，分别导致永磁体磁阻减小、磁动势增大，使永磁体提供的偏置磁通增大，进而使电机的平均悬浮力Favg呈上升趋势。而从图3(b)中可见，平均悬浮力Favg随永磁体内径的增加而先减小后增加再减小，但总体上呈减小趋势，由于永磁体内径的增大导致其磁阻变大，使永磁体提供的偏置磁通减小，最终使平均悬浮力Favg总体呈减小趋势。

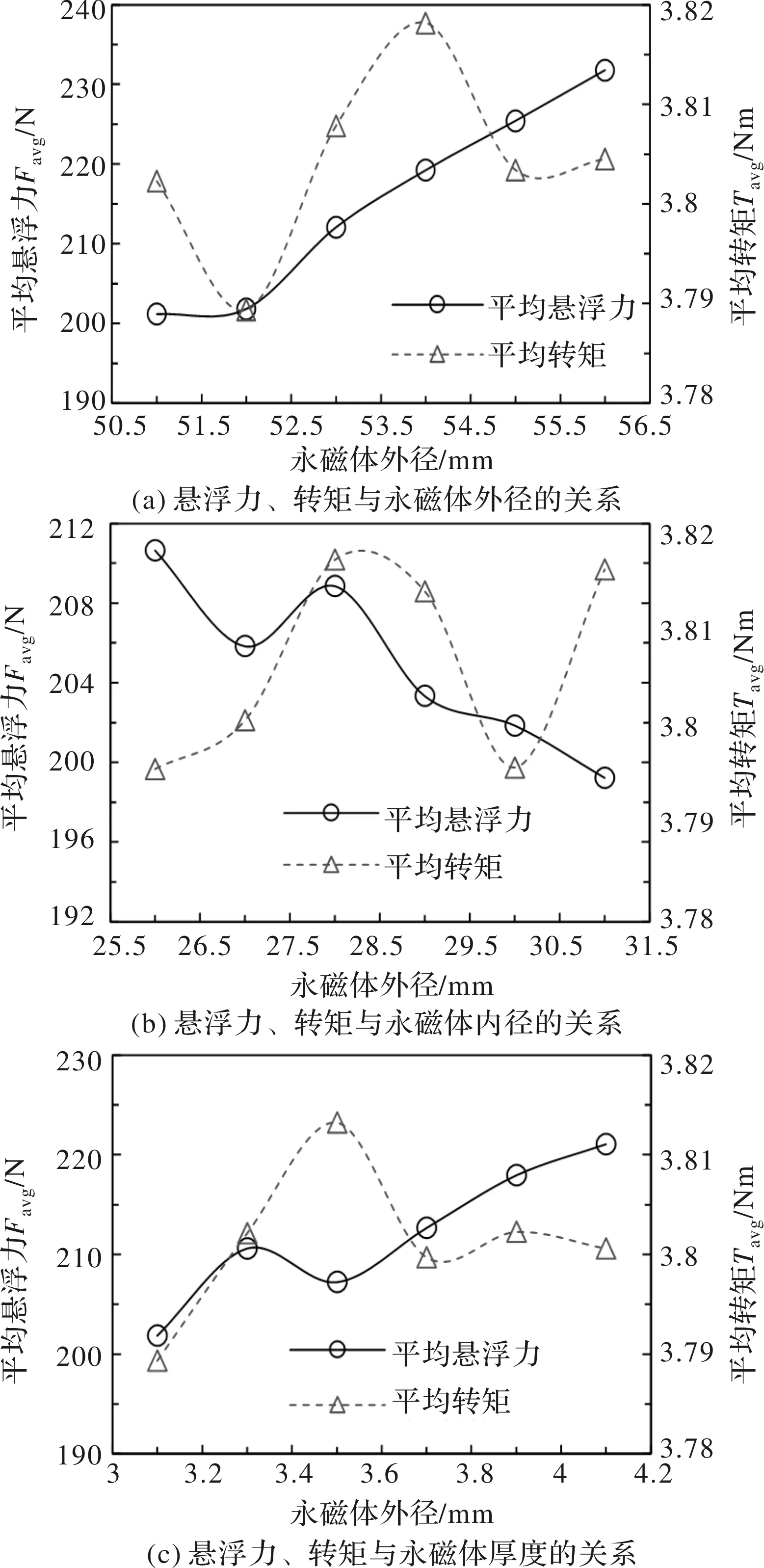
图3 悬浮力、转矩与永磁体结构参数的关系

如图3(a)所示，平均转矩Tavg随永磁体外径的增加先减小后增大再减小，但转矩总体变化幅值较小，最大峰谷值仅0.03 Nm，占平均转矩的0.8% (=0.03/3.8)。由图3(b)、图3(c)可见，平均转矩Tavg随永磁体内径和厚度的增加先增大后减小再增大，转矩最大峰谷值均为0.025 Nm，占平均转矩的0.66% (=0.025/3.8)。因此转矩受永磁体结构参数影响较小。

如图4(a)所示，平均悬浮力Favg随转子外径的增加而呈略微上升，平均转矩Tavg随转子外径的增加先减小后增大再减小再增大，最大峰谷值仅0.015 Nm，占平均转矩的0.39%(=0.015/3.8)，因此转矩基本不受转子外径的影响。由图4(b)可得，平均悬浮力Favg和平均转矩Tavg随转子内径的增加而呈明显下降趋势。由于转子内径增大，导致气隙平均长度也随之增大，进而使悬浮力和转矩明显减小，考虑到加工工艺和控制精度，气隙平均长度固定为0.3 mm，在此基础上确定转子内径。如图4(c)所示，平均悬浮力Favg和平均转矩Tavg随转子轭厚的增加均先减小后增加再减小，变化趋势较为一致。

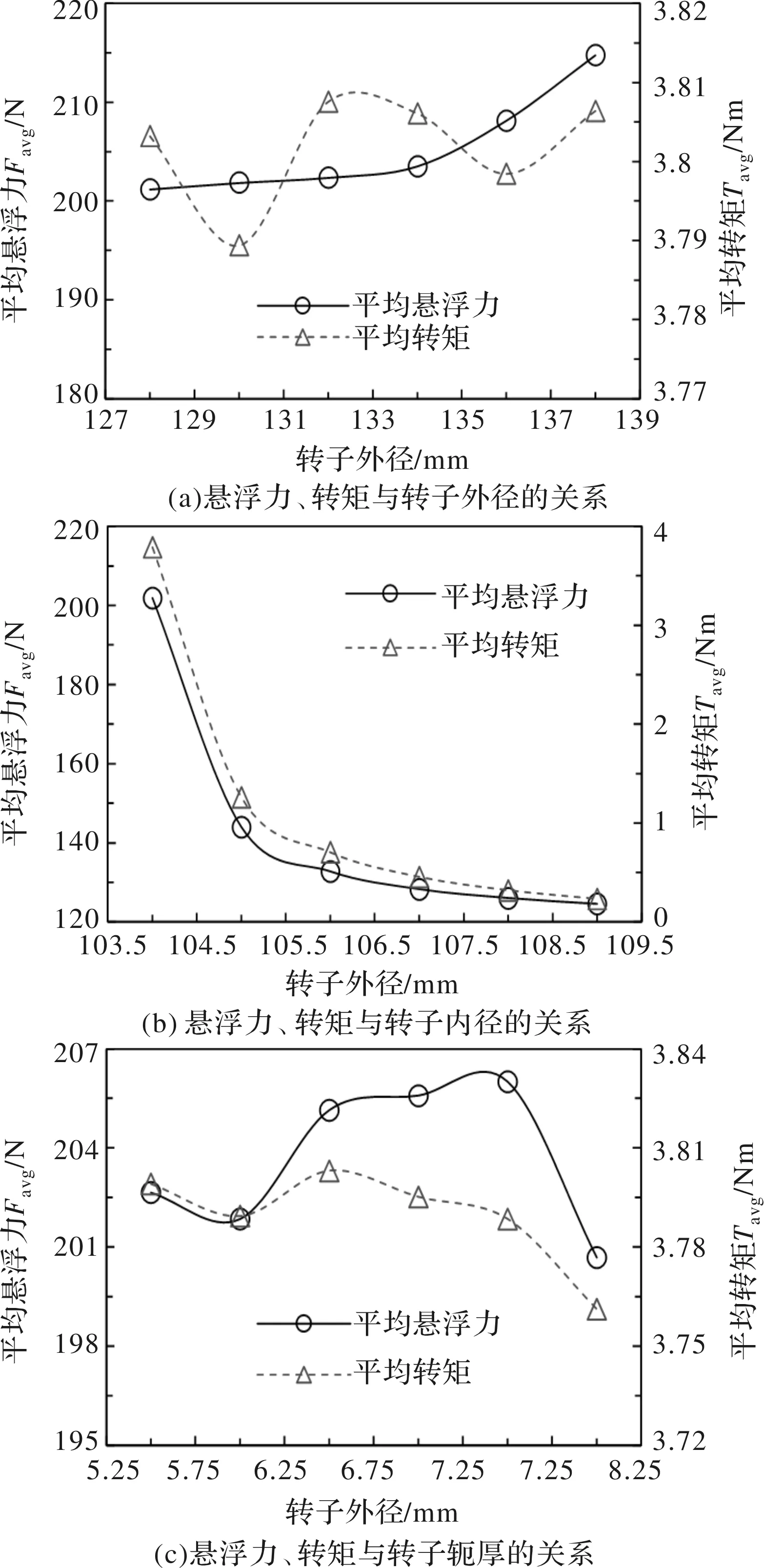
图4 悬浮力、转矩与转子结构参数的关系

如图5(a)所示，平均悬浮力Favg随悬浮极厚度的增加先减小后增加再减小；平均转矩Tavg随悬浮极厚度的增加先减小后增大再减小再增大。由图5(b)可得，平均悬浮力Favg随悬浮极齿宽的增加先增大后减小再增加再减小，而平均转矩Tavg随悬浮极齿宽的增加先减小后增加。

图5 悬浮力、转矩与悬浮极结构参数的关系

如图6(a)所示，平均悬浮力Favg和平均转矩Tavg随转矩极厚度的增加均呈现先增加后减小再增加再减小趋势。由图6(b)可见，平均悬浮力Favg随转矩极齿宽的增加先增大后减小再增加，而平均转矩Tavg随转矩极齿宽的增加先增加后趋于稳定。

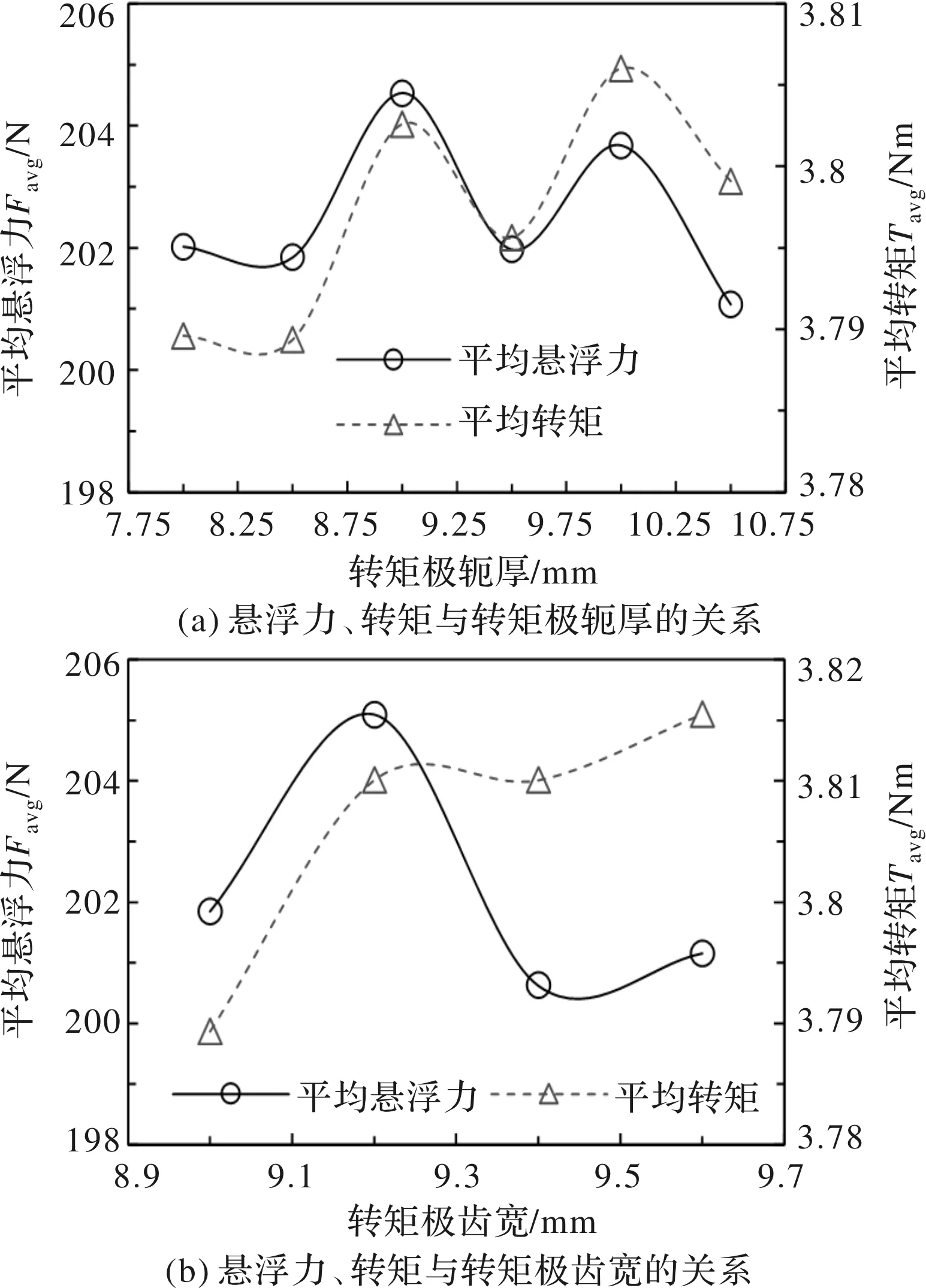
图6 悬浮力、转矩与转矩极结构参数的关系

ASP-BFM的转矩和悬浮力是其最重要的两项性能指标。为了更精确地描述电机的这两项性能指标，本文定义电机的转矩效率TP、悬浮效率FP、转矩密度TV及悬浮力密度FV如下：

(1)

并设计权重因子ωF、ωT、ωFP、ωTP、ωFV、ωTV，构建参数敏感度分析性能指标函数：

(2)

式中,Fb、Tb、FPb、TPb、FVb、TVb为各项基值(选为各项最大值)，ω为各项权值，且有ωF+ωT+ωFP+ωTP+ωFV+ωTV=1。

根据上述结构参数对性能指标的敏感度分析，最终确定待优化变量为永磁体厚度、永磁体内外径、转子轭厚、悬浮极轭厚及转矩极轭厚。

3 ASP-BFM的回归模型

将敏感度分析获取的ASP-BFM关键结构参数作为输入样本，性能指标函数fans作为输出样本，采用ELM算法构建ASP-BFM关键结构参数与性能指标函数的非参数化模型。

给定N个任意输入输出样本(xi，yj)，其中，xi=[xi1,xi2,…,xin]T∈Rn，yi=[yi1,yi2,…,yim]T∈Rm，则具有L个隐含层并且激励函数为G的ELM预测模型可表示为

(3)

式中,βi为第i个隐含层单元的输出加权值；ai为输入层到第i个隐含层单元的输入加权值；bi为第i个隐含层单元的偏置。

激励函数G可为三角函数、径向基函数及双曲正弦函数等，ELM原理如图7所示。如果具有L个隐含层的前馈神经网络模型能零误差地逼近N个样本，则ai、bi及βi满足

(4)

图7 ELM原理图

式(4)可简化为

Hβ=γ

(5)

其中，γ是期望的输出矩阵，β是输出权重矩阵，H是网络的隐含层输出矩阵，可展开为

(6)

由于隐含层的偏置和输出权重是随机给定的，因此，H矩阵是一个给定的矩阵。求解网络的输出权重可转换求解输出权重矩阵的最小二乘解，即

β=H+γ

(7)

式中,H+为隐含层输出矩阵H的Moore-Penrose广义逆。

结合ELM的学习速度快、泛化性能好的优点，得到ELM算法以较短的时间内获取电机的最优非参数化模型。

4 ASP-BFM优化设计

ELM非参数化模型为ASP-BFM的优化设计提供了优化模型。然而，ELM模型具有非线性的特点，很难保证其在电机全周期内可微、连续。PSO不受此限制，且具有精度高、收敛速度快、使用简单等优点。因此，本文基于建立的ELM预测模型，采用权重惯性调整的粒子群优化算法对目标函数进行优化。优化目标函数与敏感度分析中的性能指标函数相同，在此不再赘述。

根据轴向分相磁悬浮飞轮电机设计应用场合确定额定功率、额定转速、效率，依据各变量经验取值范围得到磁负荷、电负荷、绕组电流系数、方波电流系数、系数1至5、气隙长度的具体数值满足：

(8)

式中,ki、km分别为飞轮电机的绕组电流系数和方波电流系数，PN、nN分别为飞轮电机额定功率和额定转速，Bδ、A分别为飞轮电机的磁负荷和电负荷，λ1、λ2、λ3、λ4、λ5、λ6为常数系数，η为飞轮电机的效率，Da0、Di0、hcr0分别为转子外径、转子内径及转子轭厚，Dsw0、bsw0、βsw0、hcsw0分别是悬浮极外径、悬浮极齿宽、悬浮极极弧和悬浮极轭厚，Dsn0、bsn0、βsn0、hcsn0分别是转矩极外径、转矩极齿宽、转矩极极弧和转矩极轭厚，Dpma0、Dpmi0、lpm0分别是永磁体外径、永磁体内径和永磁体厚度，Br、Hc、φp分别为永磁体剩磁、永磁体矫顽力和永磁偏置磁通，R为飞轮电机的外磁路磁阻；为了获取稳定运行的电机参数，选取约束条件为λ1=0.6～2.5，λ2=0.75～0.8，λ3=0.8～0.9，λ4=1.2～1.4，λ5=1.2～1.4，λ6=0.5～2.6，km≈0.8，ki≈0.5，Bδ=0.3～0.6，A=15000～50000。

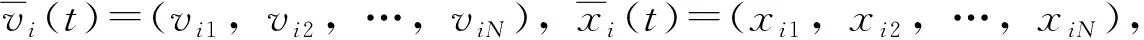
(vij(t)=ωvij(t-1)+c1r1[pij-xij(t-1)]+
c2r2[ptj-xij(t-1)])

(9)

xij(t)=xij(t-1)+vij

(10)

式中,ω为惯性因子，c1、c2为加速粒子，一般取c1=c2=2；r1、r2为区间[0, 1]上的随机数。表2给出了ASP-BFM的最终优化结构参数。

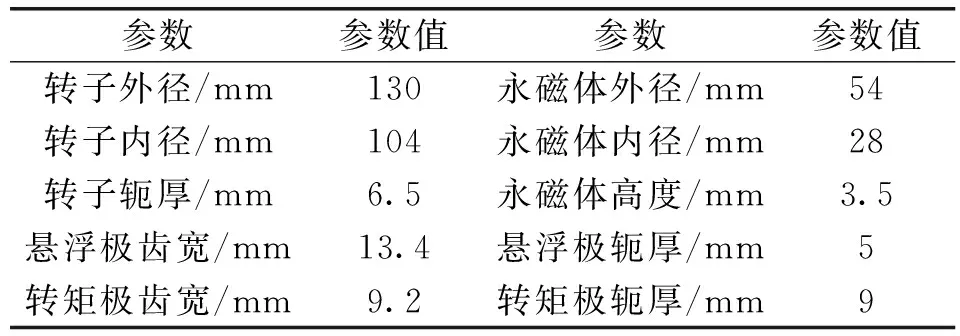
表2 优化结果

图8、图9为优化前后ASP-BFM的平均悬浮力Favg和平均转矩Tavg随转子位置角的变化曲线，对比可知，优化后电机相比于原电机在全周期范围内，即在所有转子位置角度处(0～30°)悬浮力均有所增加，平均增加了约19.04 N，平均悬浮力约提升了10.07%(=19.04/189.1)，这显然在一定程度上增强了电机径向悬浮稳定性能；同时，优化后的电机在周期内的转矩平均比原周期转矩也有所增加，平均增加了0.44 Nm，平均转矩约提升了6.67%(=0.44/6.55)，使优化后的电机获得更高的出力，提高了电机整体的利用率和适用范围。

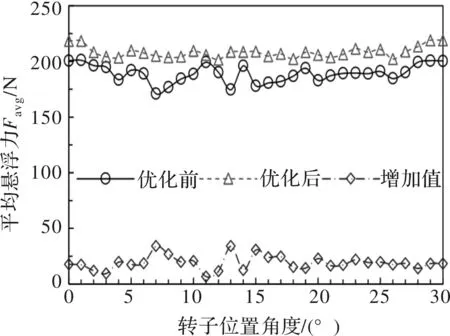
图8 优化前后平均悬浮力对比

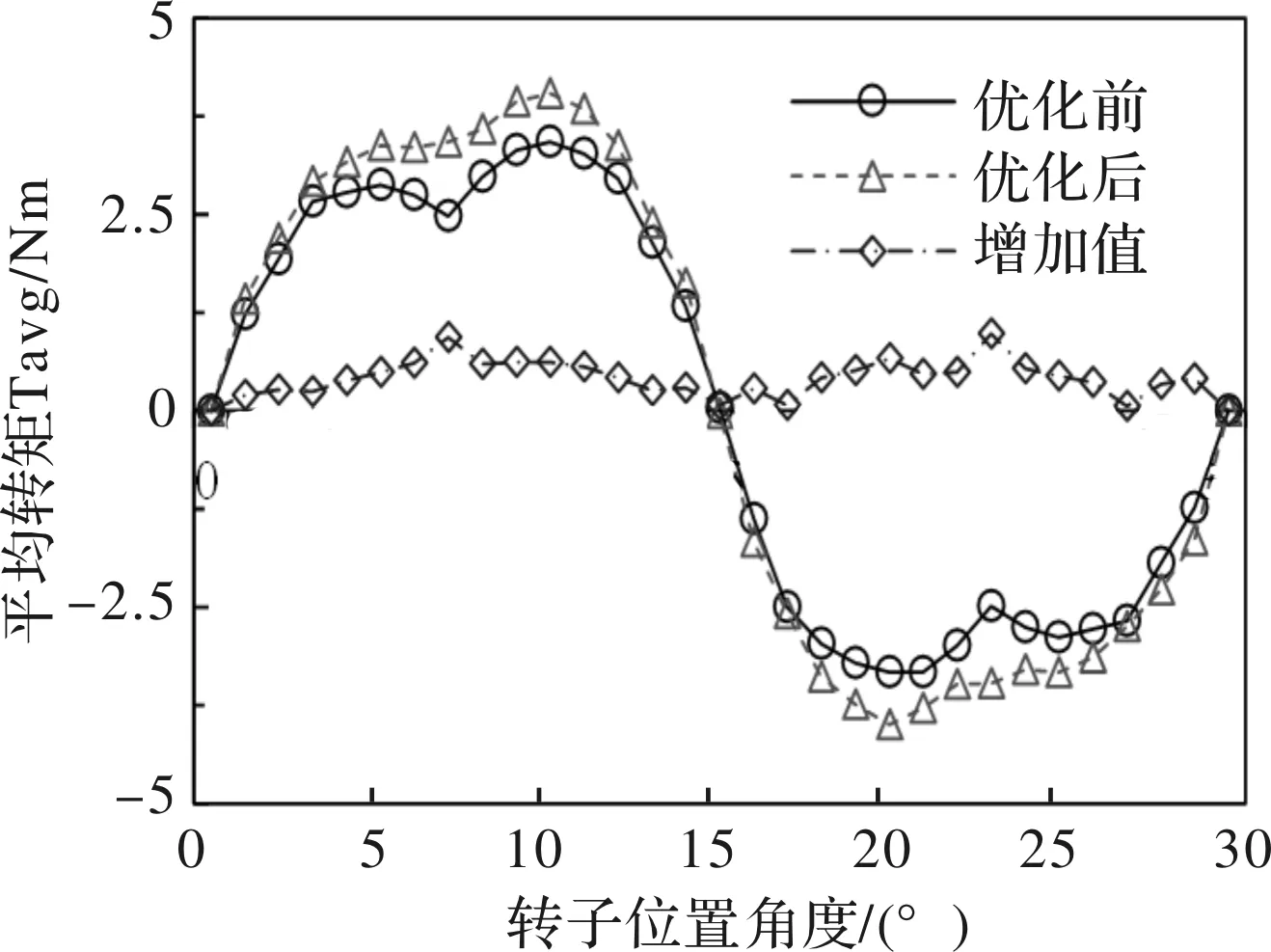
图9 优化前后平均转矩对比

5 结 论

论文基于有限元分析得出平均悬浮力、平均转矩与电机结构参数的基本规律，利用参数敏感度分析筛选起主导作用的结构参数，在此基础上构建优化目标函数，并利用ELM构建优化目标函数与主导结构参数的模型。为了实现ASP-BFM平均悬浮力与平均转矩等多目标协同优化，论文利用自适应权重调整的粒子群优化算法对优化参数进行全局寻优。对比结果表明：优化后电机悬浮力约增加了10.07%；转矩约增加了6.67%。优化后的ASP-BFM与现有12/14极和8/12极结构的电机对比，输出同一悬浮力与转矩所需绕组电流更小，降低了电机运行的功耗。