基于FPGA的异步电机半实物仿真研究

郑慧丽，赵 芳，常秀丽，连 蓉

(中车永济电机有限公司，西安 710016)

0 引 言

基于模型的半实物仿真是用真实的控制器控制虚拟的被控对象的一种试验技术，在提高控制系统的稳定性、安全性、可靠性的基础上，还可以大大缩短系统研发周期，目前已应用于航空、航天、汽车、轨道交通、电力系统等多个领域[1]。

轨道交通车辆相关控制系统的开发和维护难度都很高，依据牵引系统的开发与调试特点，为了提高开发效率、测试效率、保证产品研发质量，有必要搭建一个具有先进的数字建模与仿真测试技术的牵引系统仿真平台，进行牵引系统的半实物硬件在环仿真，能够对真实牵引控制系统进行功能与性能的全面测试[2～3]。

目前轨道交通车辆上应用最多的牵引电机就是异步电机，本文基于FPGA搭建异步电机仿真模型，提出转子磁链离散模型的优化方法，解决模型离散化的代数环问题，配置某型号机车牵引电机参数，在半实物仿真平台上与真实的牵引控制单元联调试验，给出牵引工况和制动工况试验结果。

1 异步电机数学模型

异步电机在两相静止坐标系下的电压方程和磁链方程如式(1)和式(2)所示[4～5]：

(1)

(2)

其中，usx、usy、urx、ury为定、转子电压，isx、isy、irx、iry为定、转子电流，Rs、Rr、Lm、Ls、Lr分别为异步电机的定、转子电阻、互感和定、转子自感，ψsx、ψsy、ψrx、ψry为定、转子磁链，ωr为转子转速，p为微分算子[6]。由式(1)和式(2)可得到定子电流和转子电流的计算公式如式(3)所示，是对时间的不定积分。

(3)

2 基于FPGA的半实物仿真系统

基于FPGA搭建半实物仿真模型并实现实时运行的仿真系统如图1所示。

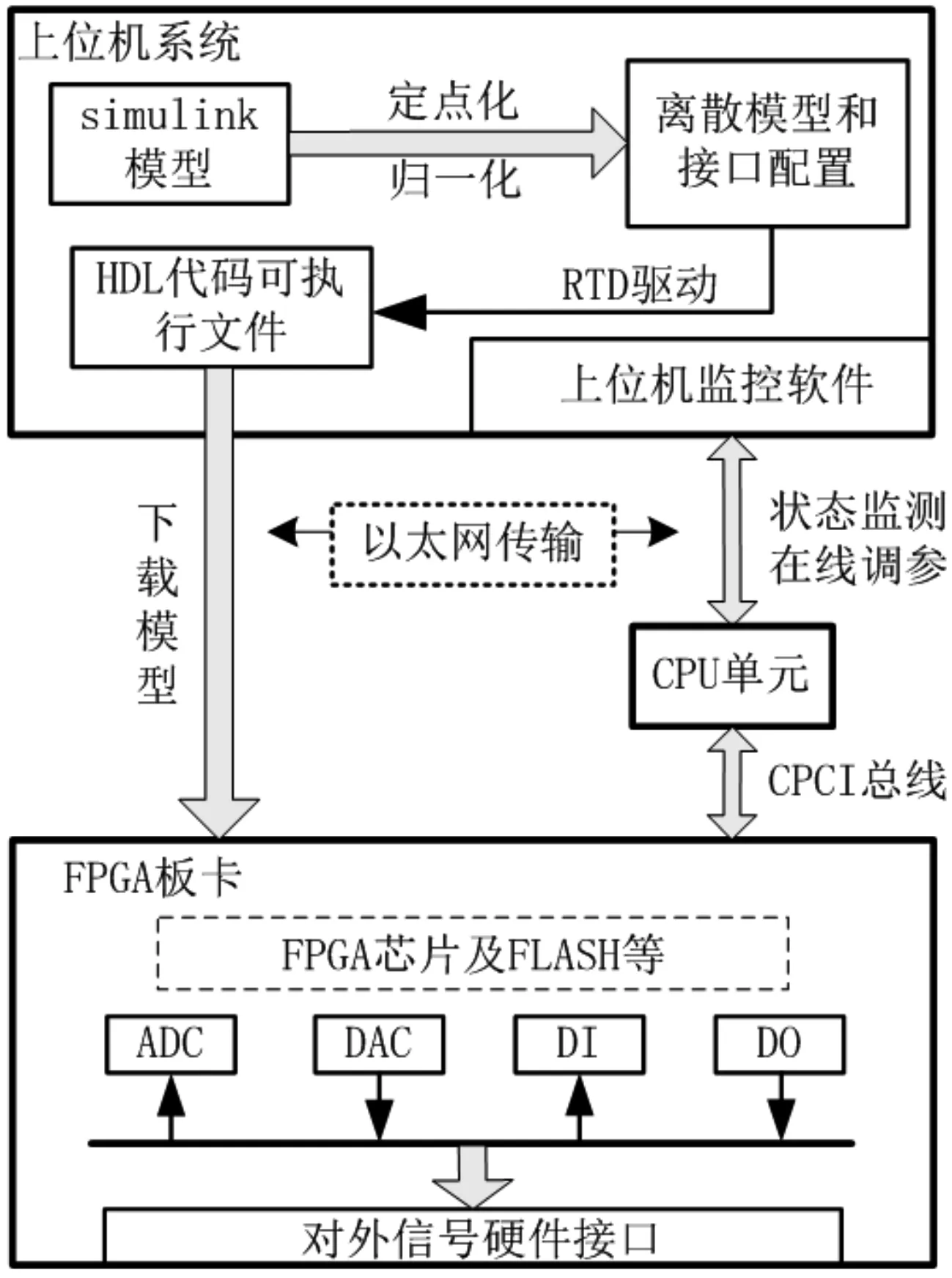
图1 基于FPGA的半实物仿真系统

在上位机系统中，半实物仿真模型基于Simulink建模，将模型进行定点化和归一化处理，得到定步长离散模型，对应FPGA硬件接口和数据格式来配置模型输入输出接口，通过定制的RTD驱动工具将模型自动编译成FPGA能识别的HDL语言代码，从而实现模型与FPGA的互联。在模型运行过程中，通过上位机监控软件和CPU单元实现对FPGA中模型运行情况进行实时监测和在线调参控制，并根据实时解算结果驱动硬件IO与真实控制器单元构成闭环测试。

基于FPGA搭建的异步电机半实物仿真模型应用于该半实物仿真系统，模型运行在FPGA板卡中，要求信号传输有很高的实时性和逻辑性能，为保证模型精度，搭建模型时应首先建立基于Simpower的模型，对比验证保证模型原理正确性，再对模型进行定点化和离散化处理，转化为可运行在FPGA中的半实物仿真模型。

3 异步电机模型搭建及优化

3.1 异步电机的模型优化

基于FPGA搭建异步电机模型时，要求模型解耦且是定步长离散化的，而转子磁链方程由式(3)代入式(2)中得到，方程中除了有ψrx、ψry状态量的反馈，还受外部输入变量ωr的影响，若直接将转子磁链的状态量ψrx、ψry反馈到前一个步长周期会引起代数环，代数环会引起信号时序紊乱，模型输出结果的不准确，因此，我们必须先对模型进行优化处理来解决代数环问题。通常，解决代数环的方法是引入Delay模块z-1，需要引入积分环节离散化后再反馈，而在转子磁链方程中，ωr会对仿真结果造成影响，当ωr较小时，ωrψrx和ωrψry造成的误差也较小，当ωr变大时，ωrψrx和ωrψry会造成较大的误差，最终导致仿真结果不准确。

为了解决这个问题，本文采用Tustin变换的方法对转子磁链积分方程进行离散化处理，重新推导转子磁链方程，破解代数环。转子磁链在连续时间函数下的不定积分方程如式(4)所示。

(4)

对式(4)进行Tustin变换后得到离散时间函数下的转子磁链方程如式(5)所示。

(5)

式中，Ts为采样周期，ψrx、ψry(k)、irx(k)、iry(k)、ωr(k)分别为第k个采样周期的转子磁链值、转子电流值、转子速度值，ψrx(k-1)、ψry(k-1)、irx(k-1)、iry(k-1)、ωr(k-1)为第k-1个采样周期的转子磁链值、转子电流值、转子速度值。以ψrx(k)、ψry(k)为待求变量求解式(5)，使方程左边只含有ψrx(k)、ψry(k)变量，前一个步长周期的转子磁链值ψrx(k-1)、ψry(k-1)存在于方程右边，式(5)即为转子磁链离散化方程，每一个步长周期内都会迭代一次电流和磁链的值，解决了代数环同时不影响信号时序，模型中依据此方程计算转子磁链。

3.2 异步电机仿真模型

基于FPGA搭建的异步电机半实物仿真模型如图2所示。

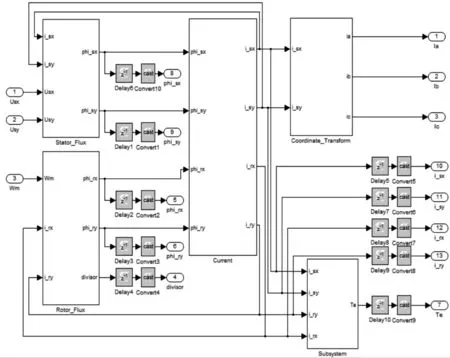
图2 异步电机半实物仿真模型

图2中模型包括定子磁链计算模块、转子磁链计算模块、定/转子电流计算模块和电磁转矩计算模块，分块搭建模型，结构清晰，易于查错和更改。信号输出端口增加一个Delay模块，用于缓存上一采样周期的数据，实现信号的并行传输，提高模型运算速率。

4 试验结果及分析

基于某机车牵引电机参数配置异步电机模型的参数，离线仿真结果与仿真软件中标准的Simppower电机模型仿真结果对比，确保半实物模型的准确性，满足精度要求的情况下进行模型转化和在线调试；在半实物仿真平台上与实际的牵引控制单元(TCU)联调，采用实车运行控制程序，完成电机全速度范围内的牵引工况和制动工况的半实物仿真联调试验。

4.1 牵引工况

牵引系统控制算法为矢量控制，分段变频控制方式：低频段采用异步调制方式，中频段采用同步调制下的SHE控制方式，当电机转速达到额定点时切换为方波控制方式。电机运行在46.97 Hz频率下的牵引系统半实物仿真试验波形如图3所示,其中CH1是直流母线电压波形，CH2是四象限输入电压波形，CH3是四象限输入电流波形，CH4是逆变输出UV线电压波形，CH5是逆变输出U相电流波形，CH6是逆变输出V相电流波形。

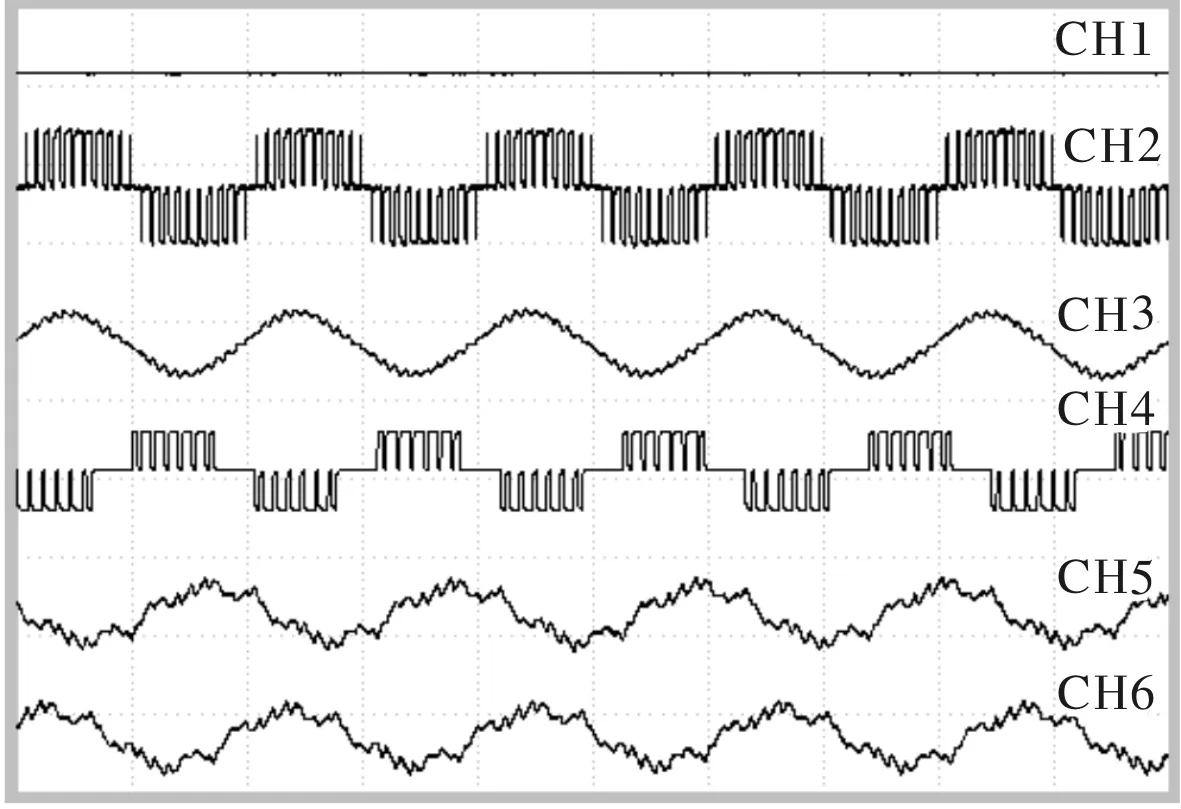
图3 牵引工况试验波形

由于半实物仿真平台上采集到的波形数据是模拟传感器信号输出的小信号，且均为电压信号，因此必须将半实物仿真结果数据导入仿真软件中进行傅里叶分析，再进行数据对比，这里只针对电机电压和电流波形进行对比分析，验证异步电机半实物仿真精度。图4为牵引工况下的半实物仿真试验与地面试验得到的全速度范围内的线电压有效值对比结果，精度值为95.38%，图5为牵引工况下的半实物仿真试验与地面试验得到的全速度范围内的U相电流有效值对比结果，精度值为95.36%。牵引工况下半实物仿真试验结果满足机车牵引系统联调试验要求。

图4 牵引工况下线电压试验结果对比

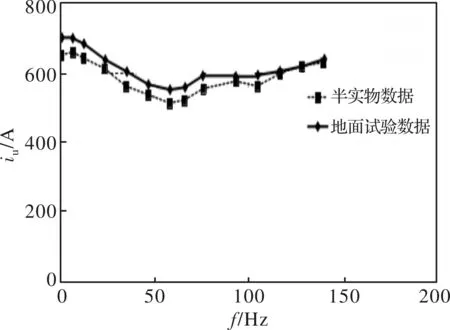
图5 牵引工况下相电流试验结果对比

4.2 制动工况

制动工况下电机运行在80.09Hz频率下的半实物仿真试验波形如图6所示，其中CH1是直流母线电压波形，CH2是四象限输入电压波形，CH3是四象限输入电流波形，CH4是逆变输出电压波形，CH5是逆变输出U相电流波形，CH6是逆变输出V相电流波形。

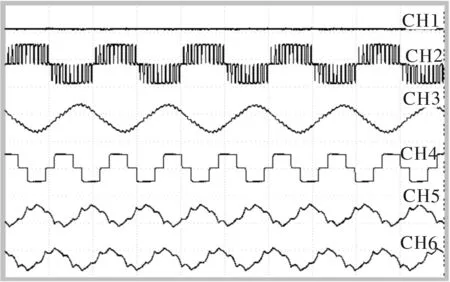
图6 制动工况试验波形

从图6中可以看出，四象限输入电压和电流相位相反，制动工况为能量回馈过程，能量从逆变器经过四象限回馈到接触网。

制动工况下对半实物仿真试验和地面联调试验的电机电压和电流进行对比分析，图7为全速度范围内的线电压有效值对比结果，精度值为96.93%。图8为全速度范围内的U相电流有效值对比结果，精度值为94.55%。制动工况下半实物仿真试验结果满足机车牵引系统联调试验要求。

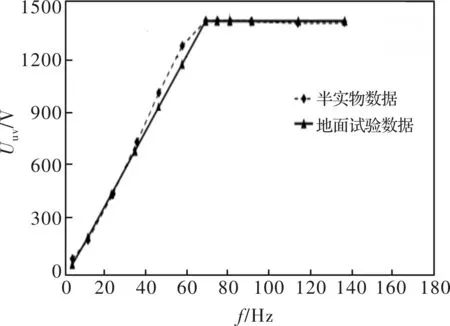
图7 制动工况下线电压试验结果对比

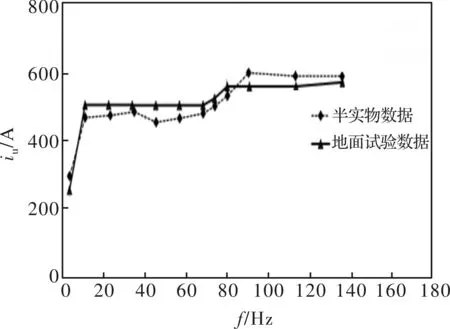
图8 制动工况下相电流试验结果对比

5 结 论

本文提出异步电机半实物仿真模型优化方法，搭建基于FPGA的半实物仿真模型，并与真实的牵引控制单元联调完成牵引、制动工况试验，从半实物仿真试验结果与地面试验结果对比来看，线电压精度均达到95%以上，电机相电流精度也在94%以上，搭建的异步电机半实物仿真模型完全满足机车牵引系统的调试精度需求，该模型可用于研究和验证以异步电机为牵引电机的机车牵引系统控制算法。由于半实物仿真模型搭建时忽略电机损耗、温差对电阻的影响等因素，因此输出电机电流比地面试验数据偏小，在下一步的仿真建模中，可根据温度、湿度等因素对定子电阻的影响来优化异步电机半实物模型，使仿真环境更接近实际。