基于Bond Graph的电机驱动转子系统振动特性研究

邹小林，王 宾，徐 永，刘洪里

(1. 四川大学 水利水电学院,成都 610065；2. 四川水利职业技术学院羊马校区，四川 崇州 611230；3. 中国电建集团成都勘测设计研究院有限公司 机电部，成都 610072)

0 引 言

由电机驱动的转子系统是工业领域中很常见的机电耦合系统，其振动问题是影响机电系统安全运行的重要因素之一；转子系统振动特性的研究也是转子动力学的重要研究方向之一[1～2]。目前计算复杂转子系统的临界转速主要采用有限元等数值计算方法[3]，而电机与转子系统隶属两套不同的系统，耦合之后涉及到大量的计算，缺少简单有效的手段在满足电机输出特性的前提下研究其驱动的转子系统的振动特性。针对电机的临界转速计算与转子振动特性研究大多着眼于电机轴系结构对转子振幅的影响[4～6]，电机的工况变化对转子振幅的影响往往没有被考虑。Bond Graph作为一种基于功率流的建模方法[7～9]，十分适合用于研究耦合系统；其独特的推导方法可以方便地获得系统的状态方程(一阶常微分方程组)，降低了耦合系统的建模难度。因此，利用Bond Graph对电机与转子耦合的系统进行建模分析具有独特的优势。

Bond Graph方法对电机进行建模已经有了初步成果，廖连莹等[10]对电动汽车的直流电机进行了建模；陈焕明等[11～12]对鼠笼式异步电动机以及交流感应电动机进行了建模仿真分析，通过分析比较均验证了Bond Graph建模方法的正确性，其模型能够很好地体现电机的输出特性。对转子系统的建模分析也得到了学者们的验证。Pedersen基于平面运动刚体的Bond Graph模型扩展得到了Jeffcott转 子系统的Bond Graph模型[13]；Campos基于Lagrangian Bond Graph法推导得到Jeffcott转子的Bond Graph模型，并设计实验验证了所得模型的准确性[14]。

本文拟将Bond Graph应用于由电机驱动的转子系统动力学建模分析，并以此模型为基础仿真分析该机电耦合系统的动力学特性，结合转子试验台考察电机工况变化及故障情况下对转子系统振动特性的影响。

1 Bond Graph建模理论

Bond Graph是美国麻省理工学院的H.M.Paynter教授于1959年提出的一种基于功率流的建模方法[7]。该方法在D.C.Karnopp[8～9]等人的进一步研究推广下逐渐成为机电工程领域成熟实用的建模方法。在Bond Graph的框架下，多种形式能量并存的系统也可以由指定的基本元件以一定的连结方式，用规定的符号表示出来，能够更加直观和清晰的得到各种能量之间的相互作用和转换关系[15]。目前，这种可以统一不同能域系统的建模方法广泛应用于各种复杂工程系统中[16]。

Bond Graph定义了势变量e、流变量f、动量变量p、变位变量q四种广义变量，其在不同类别系统所对应的物理变量如表1所示。

表1 Bond Graph广义变量对应关系

Bond Graph用键来表示功率的流向，用规定的元件来表示各种系统的内部成分。标准的Bond Graph模型中一共有9种元件：一通口元件包括势源Se、流源Sf、阻性元件R、容性元件C和惯性元件I；二通口元件包括转换器TF、回转器GY；三端口元件即0节点及1节点。以上元件的具体定义可参见参考文献[9]。

2 电机与转子系统建模

2.1 永磁无刷直流电机Bond Graph模型

选用永磁无刷直流电机作为驱动Jeffcott转子的原动机，图1显示了其内部的电磁结构。根据Bond Graph的建模规则，文献[10]完成了针对这种电机的Bond Graph建模工作，其Bond Graph模型如图2所示。

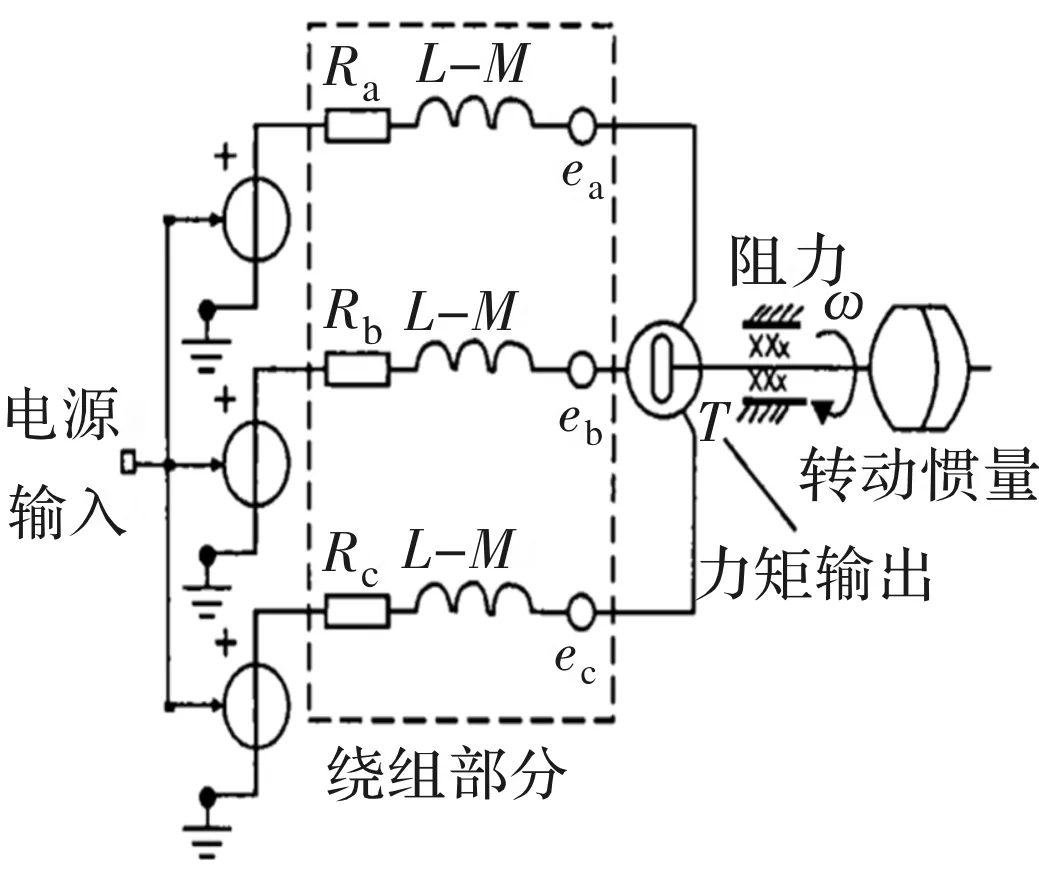
图1 永磁无刷直流电机简化模型

图2 永磁无刷直流电机Bond Graph模型

在图2中，MSe作为可变势源元件代表电机的各相电压输入，R作为阻性元件代表各相绕组电阻与转子的摩擦阻尼系数，I作为惯性元件代表绕组电感与转子的转动惯量，GY回转器代表各相的电磁转矩系数。整个Bond Graph模型输入相电压，输出转矩与转速。在此模型中，定义了4个惯性元件I，根据Bond Graph的变量定义原则，自然有4个对应的能量变量；根据0、1结构成的势、源关系结构，推导对应的状态方程如式(1)所示。

(1)

该模型形式简洁，准确地反映了电机的工作原理，故本文选用该模型与Jeffcott转子的Bond Graph模型相耦合，得到由电机驱动的转子系统Bond Graph模型。

2.2 Jeffcott转子的Bond Graph模型

如图3所示，Jeffcott转子把转子简化为单盘，两端为刚性轴承，转子质心c与轴心o存在偏心距e，是经典的单盘转子系统。

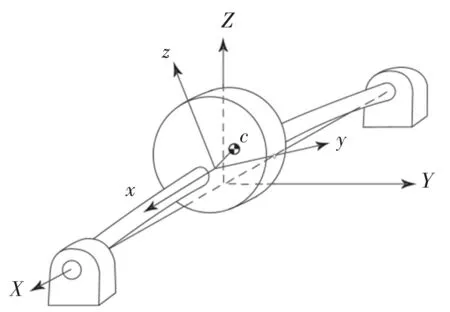
图3 Jeffcot转子示意图

Jeffcott转子质心点的运动微分方程很容易得到，如式(2)所示。为了方便上述微分方程的求解，可以把二阶偏微分方程转化为一阶常微分方程组(状态方程组)，这一般采用Hamilton法[17]。但Hamilton法求取状态方程的过程繁琐，得到的状态方程式也十分复杂。在下文中将看到，Bond Graph在求取状态方程上，有着简单快捷的优势。

(2)

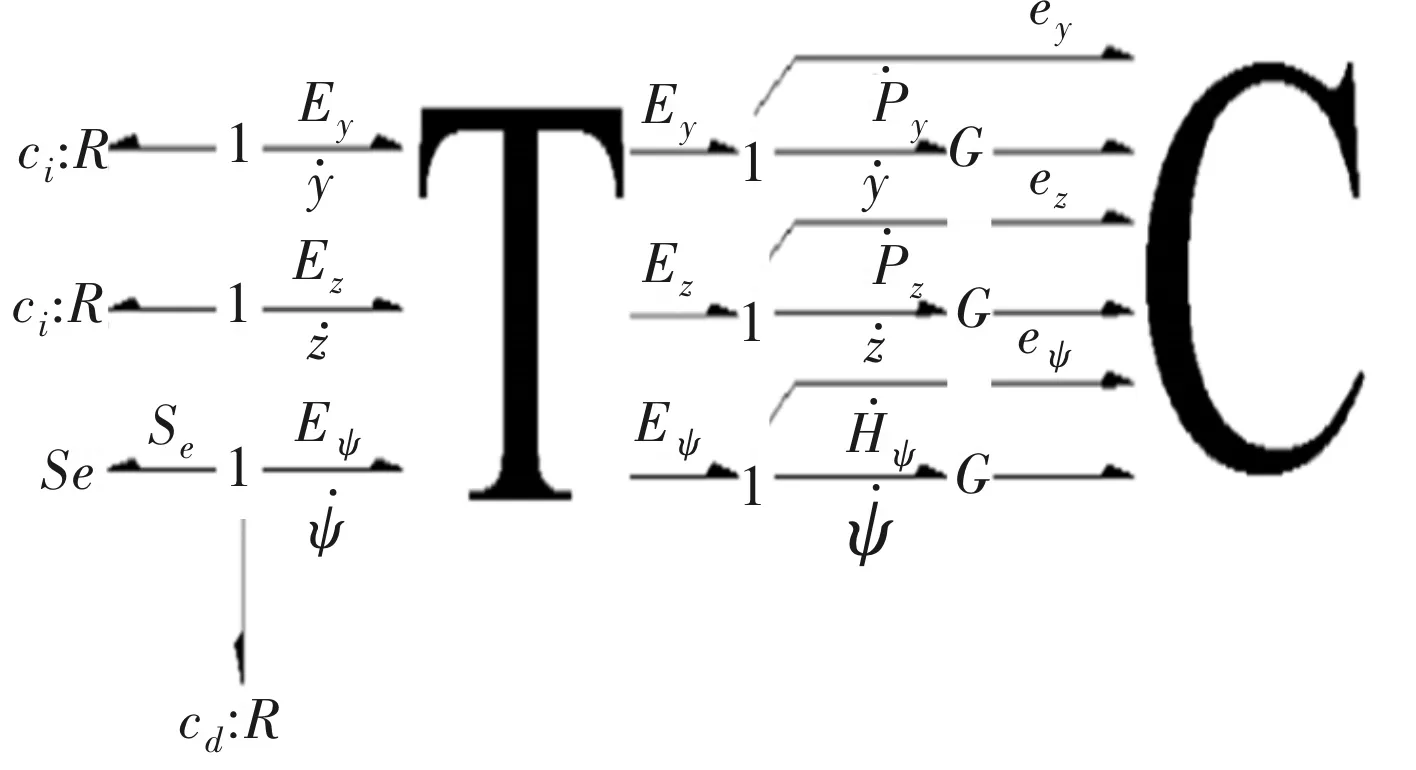
图4 Jeffcott转子Bond Graph模型

在Campos的建模过程中，把转子放入旋转坐标系描述，并引入欧拉角的概念，将其用转换矩阵T表示(这实际上是多通口的TF元件)，完成旋转坐标系与惯性坐标系的转换[12]。

为了引入转子所受的力与力矩，选用R阻性元件来代表Jeffcott转子系统中的阻尼，多通口的C容性元件代表轴的刚度与储存的弹性势能，Se势元件来代表激励输入；再使用恰当的0、1结连接，完成Jeffcott 转子的Bond Graph模型建模。同样，根据定义的变量与关系结构，得到如下状态方程：

(3)

式中，ci、cd为惯性阻尼与旋转阻尼，动量变量P与H为力或力矩。式3与传统的转子动力学方程组相比，采用了一阶常微分方程组(ODEs)，可以直接应用于面向ODEs求解的各种计算机软件。在获取系统状态方程这一点上，Bond Graph的建模方法相对于常规建模方法具有巨大的优势。

3 模型耦合与仿真

3.1 两种模型的耦合

上文给出了永磁无刷直流电机的Bond Graph模型与Jeffcott转子的Bond Graph模型，现将两种模型耦合，得到由电机驱动的Jeffcott转子系统Bond Graph模型。把Jeffcott转子模型中的Se元件与电机模型的输出部分的MSe元件相连，因为两者同在一个0结上，根据Bond Graph对0结的定义，Jeffcott转子与电机轴系伸出端同势，即电机向Jeffcott转子输入力矩(Se)带动其旋转。该模型的连接示意图如图5所示。

图5 模型耦合示意图

该模型可直接看作电机模块与Jeffcott转子模块相接得到的产物，这也体现了Bond Graph建模方法的一大优势：即模型良好的扩展性。Bond Graph模型由于采取统一变量描述各种系统，不同系统的Bond Graph模型可以在保留模型自身结构特点的前提下相互耦合。该机电耦合的转子系统模型不仅能反映无刷直流电机的内部结构关系，也能反映Jeffcott转子自身的动力学特性[18]。这将在接下来的仿真结果中得到验证。

3.2 仿真的实施办法

电机驱动的Jeffcott转子系统Bond Graph模型直接由两个Bond Graph模型耦合得到，因此直接将两个系统的状态方程组叠加，将电机输出方程(即转子系统输入方程)用参数定义的方式代入。使电机的力矩输出等于Jeffcott转子系统的力矩输入，即：

(4)

使电机与Jeffcott转子系统共用一个角速度，即：

(5)

上述两式为电机的输出方程(转子系统的输入方程)，在状态方程组中以参数定义形式加入。本文的仿真过程基于Matlab的ODE函数库编码实现。

4 实验及仿真分析

利用如图所示的转子试验台信息采集系统，从试验台获取转子系统的振动信息进行分析。信号采集系统由转子试验台、传感器、数据采集箱以及计算机软件构成。转子试验台配备有一台可调速电机、两端由轴承支撑的转子、一个减速行星齿轮箱和一个串联的磁力制动器，轴的连接处为柔性联轴器；位移传感器为电涡流位移传感器。

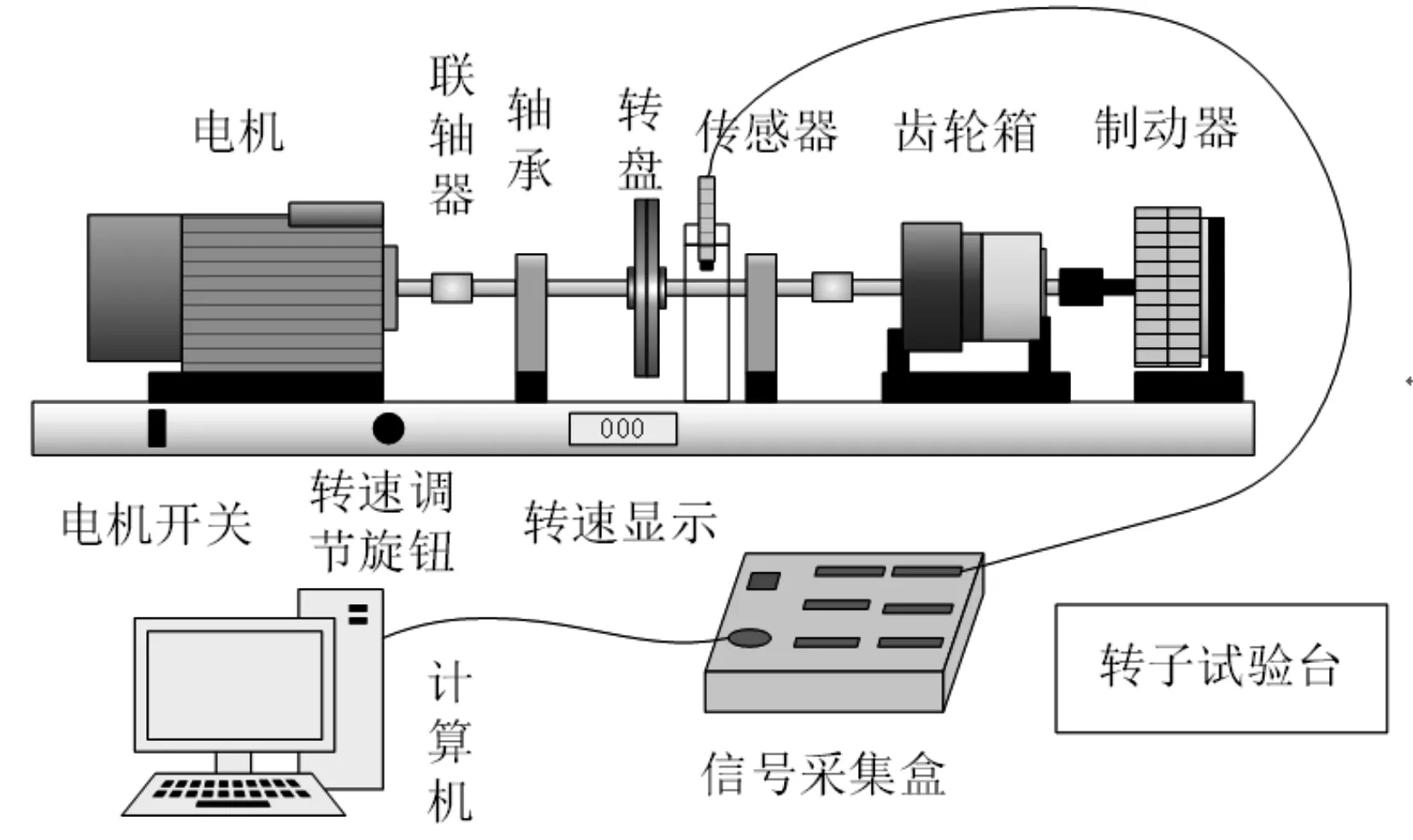
图6 转子试验台示意图

4.1 实验与仿真比较

4.1.1 实验及仿真系统参数

实验电机每相绕组电阻值为6 Ω，电机功率因数为82.5%，计算出电机绕组电感为0.5162 H。转子系统转轴质量不能忽略，转盘重2 kg，采用传递矩法计算出转子系统临界转速约为12636.58 r/min。

在仿真计算中，对电机做三相对称处理，各相的电阻值Ra=Rb=Rc=0.03 Ω，电磁转矩系数Ka=Kb=Kc=0.15 Nm/A,绕组自感La=Lb=Lc=2.45 mH,绕组互感Ma=Mb=Mc= 1.25 mH，摩擦阻尼系数Rf取0.25。为电机接上一个Jeffcott转子，该转子质量m=1 kg，转动惯量J=0.04 kg，旋转阻尼与惯性阻尼系数取1，偏心距e=1 mm。Jeffcott转子系统的临界转速值可按其固有频率估计，即其临界转速值在301.95 r/min左右。

4.1.2 转子系统动力学特性

首先对转子系统的动力学特性进行分析，比较仿真模型与转子试验台通过临界转速区时转子系统振动特性。

为考察转子在临界转速区的振动特性，使转子转速从零开始缓慢通过临界转速区。该假定工况下转子的振动特性仿真及实验结果如图7所示。

图7 电机转子系统临界转速区的振幅特性曲线

仿真模型实验中电机转速为线性增长，实验时通过均匀调节转速旋钮增加电机转速。从图7分析可得，转子的振幅在其转速达到其临界转速附近出现大幅波动。随着转速进一步升高，系统阻尼的耗散作用越来越强，转子振幅在自动定心作用下最终趋于稳定区间。

图7中仿真结果与实验结果相吻合，表明电机驱动的转子系统Bond Graph模型在满足电机输出特性的前提下，很好的体现了转子的动力学特性。

图8中给出了转子系统在稳定运行情况与转速逐渐增加并通过临界转速时的转轴轴心轨迹。相较于加速过程，稳定转速下轴心轨迹的形状更接近圆形；在加速过程中，特别是通过临界转速时，转子系统的转子轴心轨迹呈现出椭圆形轨迹，水平与竖直方向的振幅急剧增大。由此可见，临界转速区对旋转机械的正常运行具有极大危害，在实际生产工作中需要避免机器在临界转速区工作。

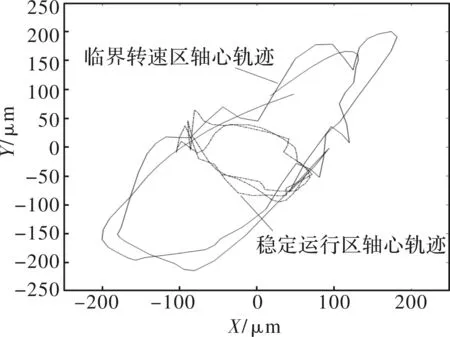
图8 临界转速区与正常运行情况轴心轨迹比较

4.1.3 不对中故障对转子振幅的影响

转轴不对中是常见的造成转子剧烈振动的故障，仿真模型计算中由横向恒定力引起的转轴不对中故障，考察电机驱动转子系统在稳态运行中突发转轴不对中故障对转子振幅的影响，仿真结果如图9(a)所示。转子试验台上通过调节联轴器的定位孔进行设置。

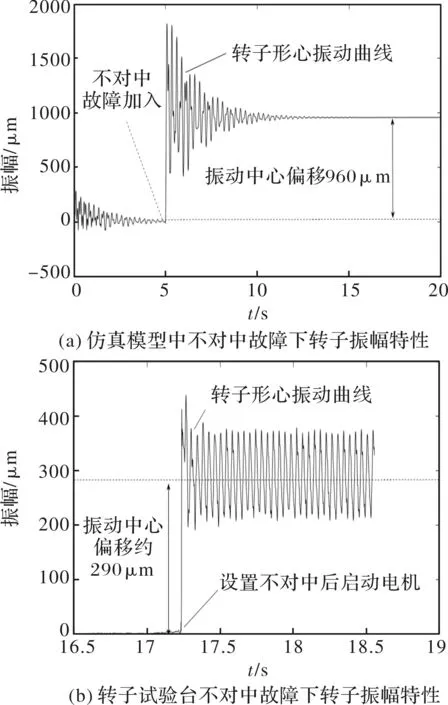
图9 电机转子系统不对中故障下转子振幅特性

从图9(a)分析可得，在由单向外力冲击引发的转轴不对中故障工况下，转子振幅骤升，随后由于系统阻尼的耗散作用，转子振幅趋于稳定，但转子形心发生偏移。转子试验台上设置不对中故障后启动电机，转子经过剧烈震动后振幅趋于稳定，转子振动的轴心发生偏移。模型仿真计算 与实验结果吻合。

图10给出了转子转轴不对中情况下的轴心轨迹，并与转子系统正常情况的轴心轨迹进行了比较。在试验台上设置好不对中故障，启动电机，转子经过短暂的剧烈振动后趋于稳定，转子的振幅变化不大。但转子的轴心轨迹形心发生了较大偏移，轴心轨迹也发生了较为严重的形变。这对实际生产过程中机械的正常运转十分不利。

5 结 语

本文建立了基于Bond Graph的电机驱动转子系统模型，通过仿真计算与实验的对比分析，构建的模型满足电机的输出特性，同时也满足转子系统的动力学特性，为研究电机工况变化与不对中故障对转子振幅的影响提供了便利。

通过计算及实验研究发现：电机转速经过转子系统临界转速区时会引起转子系统的剧烈振动，不利于机电系统的安全运行，在对电机进行调速时，要避开临界转速区以及避免反复通过临界转速区。转轴系统的不对中故障虽然不会引起转子振幅的太大变化，但会引起转子系统的轴心轨迹发生偏移，在实际生产中，要避免由外力冲击等因素引起的转轴不对中故障。