牵引电机转子铁心感应加热技术研究

袁双玲

(中车株洲电机有限公司,湖南 株洲 412001)

0 引 言

牵引电机工程制造中通常需采用热装配实现转子铁心与转轴的过盈配合。传统的烘炉加热方式由于存在加热时间长、占地面积大等缺点，越来越不能满足现代工业效率高、节能环保等要求。感应加热作为一种新型的加热方式，具备加热周期短、生产效率高、节能环保、占地面积小、加热温度便于控制等诸多优势[1]，已广泛应用于钢铁、石油、化工、有色金属、汽车、机械军工产品的零部件热处理方面，随着感应加热技术的进一步发展，其市场应用前景也越来越广阔[2]。

在实际生产过程中由于感应加热存在集肤效应、临近效应，若加热参数设置不合理，容易出现工件的心表温差较大的问题。因此如何设置合理的加热程序、提高加热效率，满足工件各个部位的温度需求是感应加热工程应用需要解决的问题。

1 感应加热的原理及特点

1.1 感应加热原理

感应加热的本质就是感应线圈中的交变电流产生交变的磁场，交变磁场穿过金属工件形成回路，在其横截面内产生涡流，从而发热实现对金属工件的加热。

感应加热的基本原理可以用电磁感应定理和焦耳楞次定理来表示。穿过闭合回路的磁通量Φ，随时间变化时，在回路上产生的电动势E:

E=dΦ/dt

(1)

感应电动势产生的涡流i，继而产生焦耳热Q，可以用焦耳定律表示。

Q=i2Rt

(2)

1.2 感应加热的特点

当等截面的导体中通过交变电流时，导体界面上的电流分布将呈现一种不均匀的状态，电流的大部分只在导体表层流过。且表层的电流密度最大，外层向内层呈幂指数规律逐渐递减。感应加热的工件中的电流也是交变电流，具有集肤效应。以圆形的工件为例，表面的电流为I0，沿工作半径x方向的电流密度为[3]

(3)

其中δ为电流的透入深度，按下式计算：

(4)

式中,ρ为工件的电阻率；μ为工件的磁导率；f为电源频率(Hz)。

由上式可以看出，电流透入深度由电源频率f、工件的磁导率μ和电阻率ρ决定。而材料ρ、μ的不变，电流透入深度由电源频率f决定。一般硅钢片的电流透入深度为3 mm～5 mm，之后电流的数值从表面向里近似指数曲线迅速衰减，中心电流很小或无电流。电流透入深度内产生的能量占总能量的86.5%，因此在电流透入深度内产生的能量用于表层金属加热，内部金属靠热传导进行加热。

根据集肤效应的电流密度分布公式，则厚为dr、高为h的圆筒状薄层吸收的功率为

(5)

dI=ihdr

(6)

dP=πphi2rdr

(7)

其中dI为半径r处的电流强度。

因此

(8)

式中，P(r)为半径为r的区域的功率。由上式可以看出功率的数值从表面向里近似指数迅速衰减。

临近效应是指当交变电流分别流过相邻两个导体，在电磁感应作用下，原本导体上均匀分布的电流将重新分布，电流偏向一侧。当两个相邻的导体流过相反的电流时，相邻两导体的内侧电流密度比外侧大得多。若通过相同方向的电流，则外侧电流密度比内侧要大一些。而对于感应加热过程中，任何时刻，工件内电流与感应线圈的电流方向都是相反的，因此电流聚集在加热工件的外表面。

2 转子铁心感应加热工艺难点分析

以某典型牵引电机转子铁心为例，铁心外径为Ф307 mm，轴孔直径Ф90 mm，铁心长度280 mm，其中转子铁心所用材料为50W470硅钢片，压圈所用材料为35CrMo钢。根据转轴与铁心/压圈的过盈量，工艺上将转子铁心加热至300℃，然后实施转轴热套。

实际生产中，由于感应加热的集肤效应，大部分的电流只从表层流过，表层(电流透入深度内)的能量占86.5%，因此表层涡流发热较大，且加热时间较短，表层来不及传热至内部，导致转子铁心内外温差较大，不仅转子铁心轴孔温度达不到热装温度，而且铁心外部还容易因为温度过高而破坏硅钢片涂层，难以满足转子铁心热装质量要求。因此在满足转子铁心生产线节拍要求(18 min)的前提下，需要采用加热-保温-加热-保温的加热模式对转子铁心进行加热，通过热传导的方式使内部得到加热。同时为了确保铁心内外温差尽可能小，工艺上采用内、外两组感应线圈和电源对转子铁心同时进行加热。

显然基于大量的试验验证感应加热程序，需要耗费大量的人力和物力，并且精确的温度测量成本高，传感器的引入也会导致温度测量结果与实际温度存在一定的偏差。为了更好地分析特定加热参数下转子铁心的温度分布情况，对牵引电机转子铁心感应加热过程进行温度场仿真分析。

3 转子铁心感应加热温度场仿真分析

感应加热产生的感应磁场在转子铁心内部的大小分布不同，导致在转子铁心中涡流产生的焦耳热各不相同。已知电源自身的功率损耗约为10%，感应线圈本身的热损耗和电损耗约为10%,则取总体加热效率为80%。通过初步理论计算，由式(8)和集肤效应，得出转子铁心在感应加热过程中的功率分布情况，根据感应加热的特点，设置合理的加热程序如表1所示。

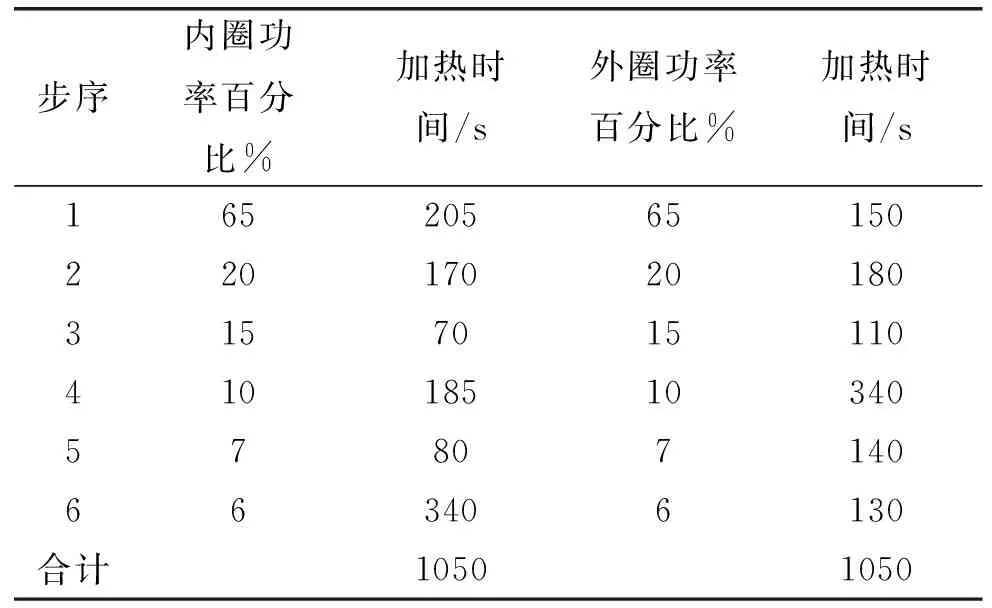
表1 感应加热程序

设置模拟仿真的边界条件：转子铁心的导热系数和比热容分别为44 W/m、400J/kg·C，转子的导热系数和比热容分别为40 W/m·C、434 J/kg·C，初始环境温度和初始模型温度为22 ℃，模型表面与空气的对流系数为10 W/m2。

仿真结果如图1所示。从温度场云图可以看出最低温度275.32 ℃位于压圈处，最高温度299.81 ℃位于铁心外侧，温差24.49 ℃，温度分布总体为外侧高内侧低。从仿真的角度来说，铁心内部温度较目标热装温度略低，因此可以考虑将主电源程序进行微调(略调高保温段的输出功率)，同时增加辅助电源的加热功率，升高下部压圈和铁心的温度，降低内外温差。

图1 转子铁心感应加热温度场云图

4 试验验证

4.1 温度采集

为了验证上述计算及仿真分析的有效性，采用主电源为80 kW，辅助电源为50 kW的双输出感应加热电源，对牵引电机转子铁心采用内、外两个感应线圈同时加热。为了获取转子铁心各部位的温度数据，在铁心不同部位点焊热电偶进行温度数据采集，热电偶分布情况如图2所示。

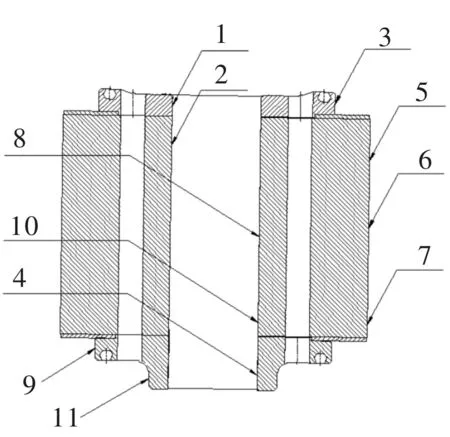
图2 热电偶位置分布图

按照如表1的加热程序，转子铁心各部位最终温度和冷却2 min后的温度如图3和表2所示。

图3 转子铁心感应加热温度变化曲线图(℃)

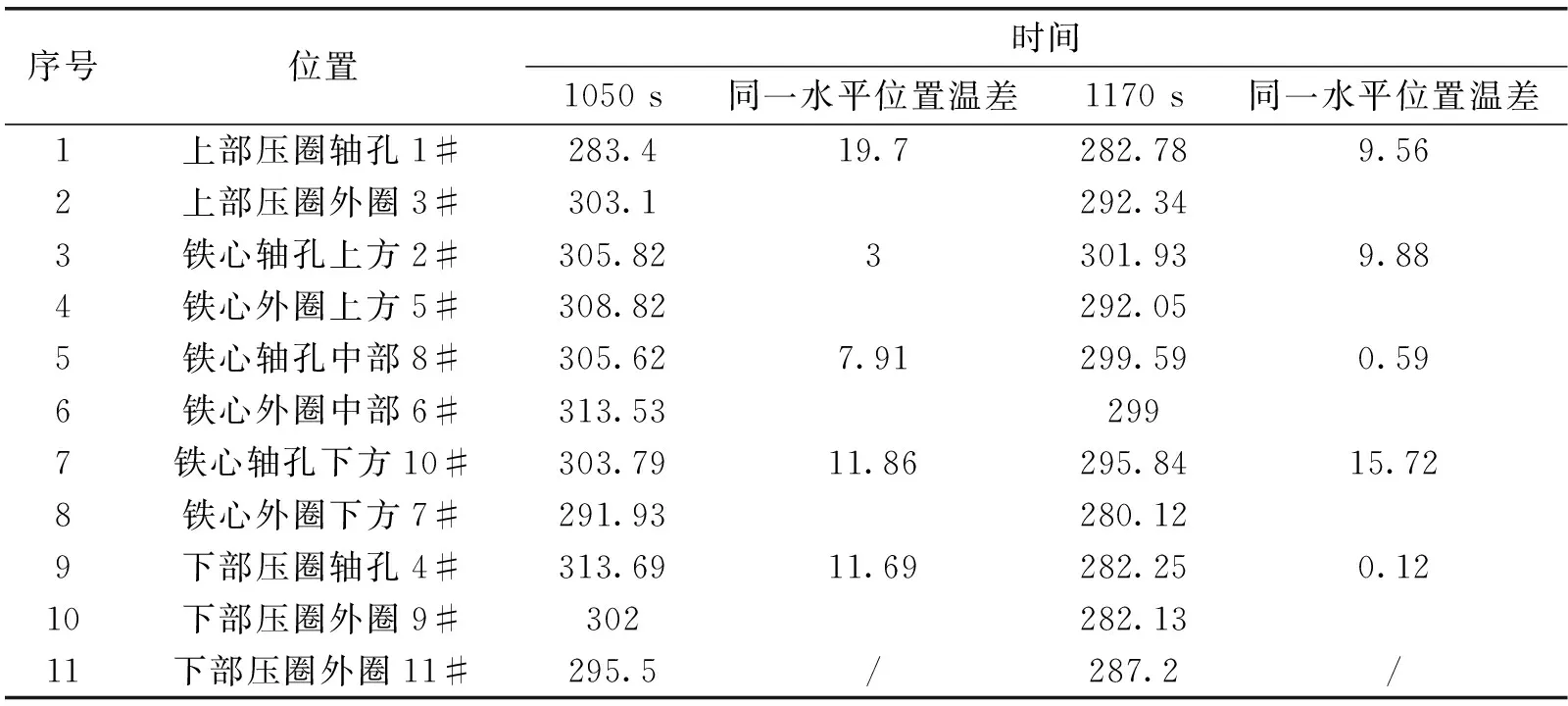
表2 转子铁心感应加热温度数据汇总(℃)

从上述转子铁心加热温度分布数据情况可以看出：

(1)转子铁心感应加热后各部位的温度在283.40 ℃～313.69 ℃之间，各部位温度均≥280 ℃，最大温差为30.29 ℃，加热过程中最高温度均≤350 ℃，加热过程中铁心温度控制在合理范围，不会对铁心硅钢片涂层造成破坏性影响。

(2)通常转轴套装作业在转子加热到温后2 min内完成，因此对转子铁心加热结束2 min后的温度情况进行检测，数据表明转子铁心各部位的最终温度在280.12 ℃～299 ℃之间，最大温差为18.88 ℃，满足产品热套温度要求。

(3)转子铁心同一水平位置的外圈温度与内圈温度差值均≤30 ℃，表明转子铁心水平方向温度场分布均匀。

4.2 尺寸检测

对加热前后的转子铁心内径尺寸进行测量，检测数据如表3所示。

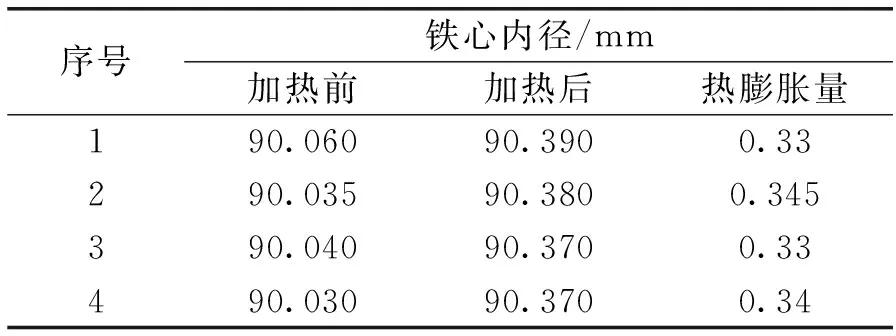
表3 转子铁心加热前后尺寸对比

根据表3试验数据，转子铁心内径的热膨胀量为0.33 mm～0.345 mm，按照铁的热膨胀系数为1.2×10-5m/℃，温度升高260 ℃，理论膨胀量为0.28 mm，转子铁心的实际热膨胀量测量值与理论值相近，满足转轴的套装要求。

5 结 语

通过理论分析、有限元模拟仿真和试验验证，采用感应加热的方式加热转子铁心的方案是可行的。针对转子铁心的温度要求、感应加热的特点，采用加热-保温-加热-保温的加热模式，设置如表1的加热程序加热转子铁心，转子铁心加热温度和内孔尺寸膨胀量符合其套轴工艺设计要求。