填数游戏中的推理经验方法运用

尚丽敏

[摘 要]一些数字排列习题之所以让学生感到枯燥无味，是因为其脱离了具体情境，缺少表象支撑和记忆依托，只有重复机械的计算充斥其中。植入简洁直观的表格能让数字排列充满挑战和趣味性，让数字推理焕发生机与活力。

[关键词]数字排列;推理;迁移;游戏

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）05-0054-03

【教学内容】北师大版教材第二册第66、67页。

【教学目标】经过填充数字游戏，使学生初步训练运算推理能力;在探究、尝试、交流、商议、辩论等一系列数学活动中体会数学实验研究的乐趣，积淀数学推理的经验。

【教学重难点】经过多级的数字推理活动，切实提高学生的逻辑推理能力，使其能够正确分析游戏规则，在交流探索中掌握填数的方法。

【教学过程】

一、谈话导入，指明目标

师：大家喜欢走迷宫吗？今天我们就来玩一个数字迷宫的游戏，具体做法是将一些数字按照要求填到方格内，使其满足全部的运算条件。这样的游戏相信大家在课外一定见识过，那么如何才能把自己训练成填数高手，完美无缺地填好每一个数字呢？这可不是碰运气，也不是一一列举能够完成的，这里面暗含玄机，大家在玩游戏时要注意留心探查其中的奥妙。

【评析：数学其实是一门好玩的学科，就看教师怎么设计。如果全部都是学科知识的堆砌和宣讲，那么学生必会反感和厌恶，因为纯数字运算全部都是抽象的数学符号和代码的演算，就像是电脑编程，没有形象思维的依托，很容易让人产生疲劳感和厌烦感，甚至让人感到头晕目眩、焦躁苦闷。如果将数學运算编入一些有趣的游戏活动中，如填数游戏，可让学生在推理探秘中感到刺激和惊喜。而且将数字运算编入方格，还可为抽象的数字及其运算关系建立清晰的形象结构支架。纷繁复杂的数学关系被方方正正的九宫格划分得整整齐齐，泾渭分明又条分缕析，既降低了重复度高、智能低级的思维量，又提高了智能化思考的含量，寓教于乐，让学生在揭秘闯关游戏中不断获得新的发现，不断寻求新的突破，不断获得成功体验，不断增加自信，不断积蓄能量。因此，导入环节的开门见山，一下子抓住学生的注意力，而且点明了学习目标，学生的学习兴趣瞬间被激活。】

二、活动探究，积累经验

第一关：初步感悟。

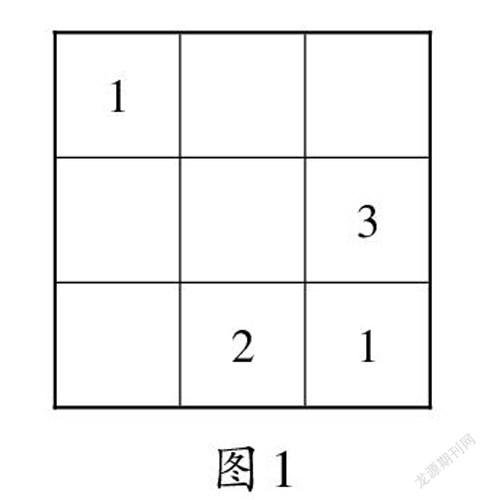
师（出示图1）：你知道怎么填吗？你觉得还需要补充条件和规则吗？

师：每个空格中只能填入1、2、3三个数字中的一个，不得超出范围，超出范围视为无效;任何一行和任何一列的三个数字各不相同，也就是说任何一行和任何一列中1、2、3三个数字必须同时出现一次，但不能重复。

师：这么多空格，从哪个空格寻找突破口？说出理由。填完第一个数字后，后面该怎么继续？有没有什么规律可循？

师：两个同学上台配合演示，说明是要观察哪一行（列）数，以哪个空格为突破口，接着又是如何继续推理和填数的。一人讲述，一人填充。

师：通过小组合作，第一关被轻松攻破，大家领悟到“填数不可盲目，一定要知晓规则”;在具体填数时也不是盲目试探，需要总结出一定的规律方法，并按照这种规律方法来推理填数，每填一个数都要综合考虑所在行与列的影响;填完数后还要根据规则一个个检查，如有失误，及时调整。

【评析：先隐瞒填数规则，让学生无从下手，学生在屡屡碰壁后领悟填数困难的原因是缺少规则。这种设陷阱的做法，是为了让学生在思维受阻时能够自我觉醒，有利于加深学生对规则重要性的认识。教材提供的表格中，每个“突破口”的答案都为3，为了避免这种巧合误导学生归纳出“填数应该先填最大数3，再填其他数”的荒唐结论，教学中教师应对表格做适当改动，堵住这种设计上的漏洞。

即使是游戏，也不可视为“儿戏”，不能让游戏的娱乐性冲散了数学的严肃性，但是又不能过于呆板，失去游戏的趣味性，这就需要教师精准地拿捏。出示九宫格后，教师首先问学生没有规则行不行，是不是想怎么填就怎么填。学生当然不会同意，因为这样任性胡来反而失去了趣味。这个规则不是教师强加的，而是学生自动提出的，这种让学生反客为主的做法为之后学生严格遵守游戏规则提供了思想保障。而这个游戏的规则实际上就是数学规则，教师出示填数规则后，引导学生进行两次思考，诱导学生发现解题的规律。这两个思考很有层次感和逻辑性，确定第一个数的方法就是后续确定其他数的依据。在学生慢慢摸索出一些门道后，教师开始小结，小结也只是方向性指导，而不是具体操作步骤的传授。】

第二关：深入感悟。

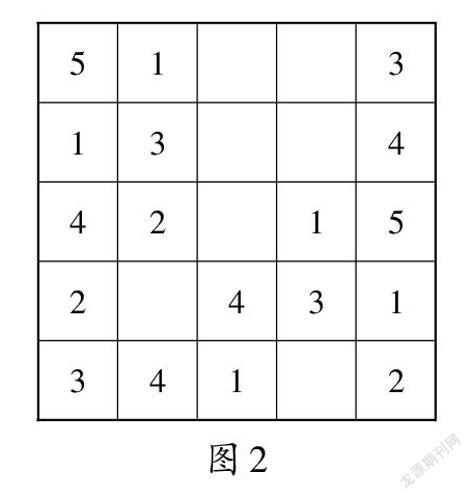
师：结合图2，猜想填数规则。

出示游戏规则：

（1）每个空格所填数字只能是在1、2、3、4、5五个数字中挑选一个。

（2）每一直排（行或列）的五个数字不能重复。

师：独立尝试填数，遇阻时可以组内讨论。

师：为什么都以下面三格为突破口？（只剩下一格空缺的可以直接推理出来）

师：剩下四格较为集中，无法直接根据所在行与列推理出数字，你是怎么思考的？（预设学生的答案：第一行两格必填2和4，第三列已有数字4，所以第一行第三列空格处只能填2，于是，第一行第四列只能填4;第一行两格必填2和4，第三列必填2、3和5，第一行第三列这一空格必须满足以上两点，所以填2。）

师：闯过第二关后，可总结经验，填数时有时只需根据一行就可判定，有时则需要行列兼顾。

【评析：猜想游戏规则增强了学生对这类题型的熟悉感，揭示了这类题型的一般特征和设计思路，同时也是对学生活动经验的总结和应用。随着游戏难度的加大，在原有推理经验不够用的情形下，学生延续原有的方法继续探究，通过独立思考后的交流发现，当单独一行或一列无法确定数字时，需要统筹兼顾行和列。至此学生的推理能力得到发展，思维的严密性得以强化。

有了第一关的经验，学生不仅对填数方法有了初步的了解，而且对游戏规则也是谙熟于心。第二关增加了方格数和难度后，规则不变，这时教师让学生自己设定游戏规则，其实就是对游戏规则的重申与自建。这次，教师开始深入到策略方法指导上，直接挑明应该先填下面三个空，让学生思考原因以及让学生说明为什么不能先填上面四个空。这种“能填与不能填，先填与后填”的对比，让学生摸索出填数的一般流程。当然，这种方法的归纳离不开第一关的思想指引。第二关还存在一个思维转折点，就是需要综合考虑交叉行与列的数字分布情况，综合推断出交叉处应填的数字。】

第三关：综合运用。

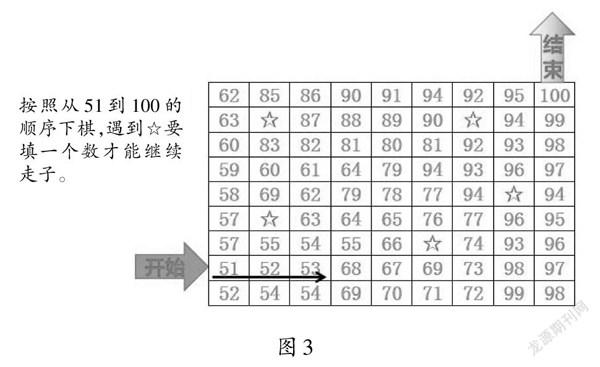
师（出示图3）：仔细观察表格，思考该怎么移动棋子。（让一学生介绍部分走法）

师：横向走子到53之后，上下两格都是54，为何上行？（因为下面的54邻边没有55，走入绝路;而上面的54旁边还有55，是活路。）遇到空格怎么办？同桌合作探究，寻找方法。

师：这关游戏暗藏机关，走到岔道口时，如何开路？要多看几步，不要只顾眼前，要“做查”同步。

【评析：第三关游戏将推理难度推至顶峰，在已有的“明确规则—寻找方法”的基础上补充随时检验和预判的方法。通过改变教材中箭头的终点位置，由56处提前至53处，借机提问“为什么这样走”，启示学生思考岔道口该如何抉择。只要找到了决策依据，填数就是一个执行问题。从走法介绍到同桌合作，再到组长展示汇报，“岔道口该如何抉择”这一难点被成功破解，学生的推理能力迈上新台阶。】

三、拓展延伸，运用经验

1.改编游戏

师：其实游戏都是人编出来的，只要肯动脑，你们也能创编出好玩的游戏。我们不妨就地取材，改编第一关的游戏，创造新玩法。（学生会想到变更游戏规则或者数字范围）

师：大家的点子很新奇，但是新规则和新数字是否合适，有待查验。

2.了解九宫格

师：老师也来改写一下规则，保留这九个空格（如图4）。（1）把1～9这9个数字不重复、不遗漏地填到空格中，每个空格中刚好填一个数字。（2）使每一行、每一列对角线上的一排3个数字相加的和都为15。这个游戏“难如登天”，大家可以挑战一下自己。不过这个游戏可不是老师的原创，它叫“九宫图”，是古人发明的，前面所有的填数游戏都属于这类数独游戏。

【评析：借助改编第一关的九宫格游戏，降低了填数游戏的神秘感，学生更是通过自创游戏提升了自身的推理能力和创造力;运用推理创编游戏，验证游戏的合理性，扩大了学生的思维辐射面，丰富了学生的思维方式，推理形式也得到了拓展，学生学习的新鲜感再次增长;巧妙地引出我国古人发明的“九宫图”，在渗透数学文化的同时进行了情感态度与价值观的渗透。

当学生熟练掌握不可重复的填数游戏后，就应该对其进行升华拓展，因为尽管学生掌握了方法，但是他们未必掌握这种方法的精髓。填数游戏的“真经”就是要学会兼顾，综合考虑各种因素来做出决策，所填数字要满足所在行和列的要求，这就是对综合处理信息能力的考查和考验。学生有没有具备这种能力？这种能力强还是弱？这些问题都需要进一步检验。增加综合难度则是最佳的训练办法，将游戏第一关的九宫格改编后，各行各列数字不仅不能重复，还需要包括对角线在内的各组数字加起来的和为15，增加的这一个条件，其实就是对综合信息的升级。虽然学生不需要顾及同行同列数字的重复性，但是各个方格之间的关联性更加抽象，学生需要兼顾的因素更多，逻辑性更强，线索更隐蔽。正是在这样的答题训练中，才能更好地锻炼学生的信息处理能力和决策能力。】

填数游戏绝不仅仅是逻辑推理那么简单，也不是寻常的推理游戏可比的，其中的数学学科专业含量比一般益智游戏要高得多。在分析一个个数字时，学生要考虑多重因素的制约和影响，这就是综合分析能力的体现;还要从中筛选合格数据，排除不合格数据，筛选和排除同样体现有序思维的特征。学生的思维只有在有序思考中才能变得严密，思维习惯也才能变得科学合理。

[ 参 考 文 献 ]

[1] 陈静.学生逻辑推理能力的培养策略[J].小学教学参考，2021（8）：81-82.

[2] 高君.小學数学核心素养下学生的推理能力培养策略[J].教学管理与教育研究，2020（23）：63-64.

[3] 张学群.基于三大“落点”，引导合情推理[J].数学教学通讯，2020（28）：87-88.

（责编 黄春香）