明确问题指向，促进有效教学

王颖

[摘 要]目前，课堂教学中的问题设计依然存在着指向不明、片面追求数量、质量不高等问题。从问题设计的指向性角度提出优化问题设计的基本途径，以启迪学生思维，发展学生数学素养。

[关键词]问题;设计;指向性;小学数学

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）05-0087-03

爱因斯坦曾言，提出一个问题往往比解决一个问题更重要。教师恰到好处的提问，能够引起学生的好奇心和思考欲，燃起学生对知识的探究热情。然而，目前的课堂教学问题设计依然存在着指向不明、片面追求数量、质量不高等问题。笔者从问题设计的指向性角度论述优化课堂提问策略的基本途径，以期能够起到抛砖引玉的作用。

一、指向比较，探寻知识缘由

教育家乌申斯基认为，比较是一切理解和思维的基础，我们正是通过比较来了解世界上的一切。基于小学生的认知规律，小学数学教材在编排上呈现出明显的螺旋式上升的特点，不同年级、不同学段的数学知识看似是一个个独立的模块和单元，实则前后内容之间具有密切的关系。教学中，教师在提问时应指向前后知识的异同点，通过比较，能够使学生了解知识的来龙去脉，把握知识的内在逻辑关联，从而帮助学生获得对知识的深刻理解，最终促进学生的深度学习。

【例1】“异分母分数加减法”教学片段

师：我发现不少同学写出算式1/2+1/4=1+1/2+4=2/6=1/3，這是错误的。那么，为什么同分母分数可以直接相加减，而异分母分数不能直接相加减？

生1：因为分母不同，分数单位不一样，所以不能直接相加减。

师：为什么分数单位不一样就不能直接相加减？有人能为我们详细解释吗？

生2：比如，1元和2元加在一起是3元，因为它们的单位都是元，但是1元加2角既不是3元也不是3角，它们的单位不同，不能直接相加减。分数的加减法也是同样的道理，同分母分数的分数单位相同，可以直接把分子相加减，而异分母分数的分数单位不同，不能直接相加减。

生3：我们在学习整数加减法时，把相同数位上的数字相加减，即把个位上的数字和个位上的数字相加减，十位上的数字和十位上的数字相加减，这是因为相同数位上的数字单位都相同，比如个位上的5都表示5个一，十位上的3都表示3个十。

师：那应该如何解决这个问题呢？

（学生在讨论后一致认为，应该用通分的方法把异分母分数转化为同分母分数，这样分数单位相同了，就可以直接按照“同分母分数加减法”的运算法则进行计算，如图1所示）

教师问题设计的指向性决定了学生思考的方向，也决定了学生思考的深度。教师从“同分母分数加减法”和“异分母分数加减法”的异同切入，巧妙设计问题，既找到了前后知识之间的联系，又使学生能够从分数单位的角度思考问题，从而获得对知识的本质认识，使学生不但知其然，而且知其所以然。

比如，在教学“笔算除法”时，教师往往将教学聚焦在除法竖式中每一步计算的算理上，力图让学生在理解算理的基础上把握竖式计算的方法。这样的教学自然是无可厚非的，然而，在此基础上，教师不妨提出这样的问题：“在学习乘法竖式时，我们是从低位开始计算，但是为什么在学习除法竖式时，却要从高位开始计算呢？”然后，教师引导学生以16×3和56÷2为例进行探讨。学生通过探讨会发现，乘法竖式之所以要从个位算起，是为了更好地处理进位，这是由数学中满十进1的规则决定的。关于为什么除法竖式要从高位计算，教师可以采取“试错”的策略，让学生尝试先从个位计算。这时候，学生发现56÷2个位商3，但是十位上的5并不能被2整除，这样就遇到了问题。然后，教师引导学生转换思路，尝试从十位除起，学生就能体会到从高位除起方便处理余数。

教师将问题指向乘法竖式和除法竖式算法的合理性，使学生通过对比和分析，对这些知识有了更加深刻的认识，从而促进深度学习的发生。

二、指向根源，探寻知识本质

《道德经》中有言：“道生一 ， 一生二 ， 二生三 ， 三生万物。”这里的“道”，可以理解为事物的本质。小学生以形象思维为主，在把握知识本质方面往往会感到力不从心，对知识的认识往往浅显化，只能达到“所见即所得”“就事论事、就题论题”的层次。在教学中，教师问题的设计应该指向知识的本质，使学生透过知识的表面现象深入挖掘，领悟知识的本质，从而增强对知识的认知，提升数学理解力。

比如，在教学“四边形的不稳定性”时，笔者会引导学生进行实验一：用四根木棒做成一个四边形框架，再用手拉动这个四边形框架，四边形框架就会变形。据此，笔者引导学生得出结论：四边形具有不稳定性。细细想来，这个实验不免令人生疑：能用手拉动框架就说明四边形具有不稳定性吗？为此，笔者进一步优化了教学设计，在上述步骤的基础上引入了实验二：笔者引导学生用四根硬纸条做一个四边形框架，把四边形框架各顶点上的两条边都粘在一起，然后让学生用手拉动四边形框架。学生发现这个四边形框架不会变形，但如果用力过猛，就会把四边形框架拉破。笔者提问：“实验二中的四边形框架不容易变形，是不是说明四边形也具有稳定性呢？我们应该如何理解不稳定性？”学生讨论后，笔者引入实验三：让学生用2张长5厘米的纸条和2张长10厘米的纸条拼成四边形，看看各个小组拼成的四边形是否一样。学生通过实验三发现，尽管使用的实验材料相同，但是拼成的四边形却各不相同（如图2）。据此，笔者总结：“我们所说的四边形易变形或具有不稳定性，指的是尽管四边形的四条边的长度都确定了，但是它的形状却是可以变化的。”

在实际教学中，不少学生在理解三角形的稳定性和四边形的不稳定性时，往往得出“拉不动就是具有稳定性，拉得动就是具有不稳定性”的结论。学生的认识如果止步于此，就说明他们还没有触及知识的本质。教学中，笔者采取对比实验法，针对“什么是不稳定性”这一问题巧妙设问，使学生意识到四边形的不稳定性并非简单的“拉得动，易变形”，并理解不稳定性指的是“尽管四边形的四条边的长度都确定了，但是它的形状却是可以变化的”，进而消除了学生的认知误区，使学生获得了对知识的本质认识。

三、指向应用，明确知识价值

数学从生活中来，最终为现实生活服务。数学家华罗庚曾说：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学。”从认识论的角度看，数学学习的过程是一个从感性认识到理性认识的过程，而从理性认识到实践是认识的又一次意义更为重大的飞跃。读书是一种学习，实践也是一种学习，而且是一种更为重要的学习。教学中，教师应该转变“知识本位”的教学思想，在设计问题的过程中，关注知识的实际应用，培养学生理论联系生活的能力，发展学生的应用意识，使学生感受到数学学习的价值。

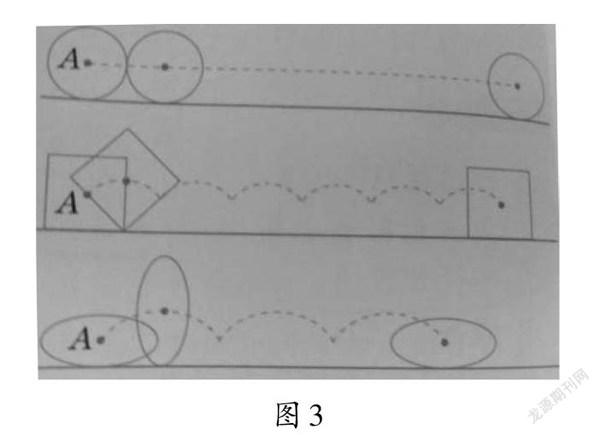
比如，在教学“圆的认识”时，笔者设计了这样的问题：“为什么自行车、摩托车、小汽车的车轮都设计成圆形？为什么不把车轮设计成正方形或者椭圆形？”学生结合教材内容展开了分析和讨论，得出结论：如图3，点A代表车轴，当正方形车轮和椭圆形车轮滚动时，在不同位置轴心到地面的高度不相等，点A的运动轨迹是曲线，这会导致车轮滚动起来后车子比较颠簸，不平稳;而圆形车轮在滚动时，轴心到地面的高度就是圆的半径，圆的半径是始终不变的，所以使用圆形车轮，车子在运动的时候是平稳的。

教学中，笔者把圆的特征和生活实例相结合，设计了具有趣味性和知识性的问题，实现了數学知识与生活应用的对接，让学生带着热情去学习新知识，不但使学生加深了对圆的特征的理解，还使学生意识到数学知识在现实生活中的应用价值。

【例2】“三角形的稳定性”教学片段

师：生活中哪些物体中含有三角形？

生1：自行车车架、篮球架和电线杆架等。

师：这些物体中的某些部位为什么要设计成三角形？

生2：这样比较牢固，不容易变形。

（教师出示桥梁、衣架、金字塔等图片）

师：既然三角形这么好，我们学校的电动伸缩门为什么不做成三角形的呢？

生3：做成三角形的不方便打开和关上。

师：三角形和四边形各有特点，在运用时要根据实际情况选择，这样才能让它们为人类造福。

教学中，笔者以数学与生活的联系作为切入点设计问题，引导学生分析三角形的稳定性在现实生活中的运用，架设起知识与生活之间的桥梁，使学生感受和体验到数学的价值与魅力，并在对知识的应用中促进对知识的理解。

四、指向整体，促进知识建构

苏霍姆林斯基曾言，揭示未知和已知之间的深刻联系，是培养学生对知识的兴趣的教育诀窍之一。由于课时划分等现实因素的影响，数学教材不得不把原本紧密相连的知识划分成一个个单元和章节，以方便教师分课时完成教学任务。这样就使得学生通过每课时获得的知识是相对独立的，学生难以真切体会知识点之间的联系，这不利于学生从整体上理解知识。实际上，数学学科知识具有较强的关联性，新知识往往是旧知识的延伸和发展，同时又成为学习后续知识的基础，旧知识与新知识相互关联，形成了一个系统性的知识网络。在教学中，教师问题的设计应指向整体，帮助学生建立起新旧知识之间的联系，从而促进学生对知识的整体建构。

【例3】“认识平行四边形”教学片段

（教师引导学生拉动长方形框架，使长方形变成不同的平行四边形，然后再拉动框架使平行四边形变成长方形）

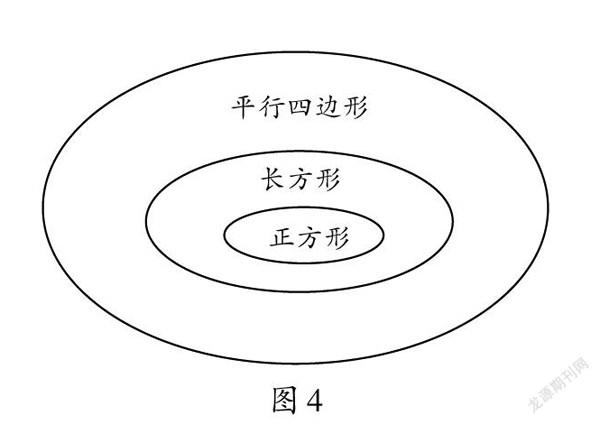
师：请同学们说一说平行四边形、长方形和正方形三者之间的关系。

生1：我通过比较，发现平行四边形和长方形的相同点是两组对边分别平行，因此，长方形也具备平行四边形的特征，属于平行四边形，但是长方形四个角都是直角，因此长方形是一种特殊的平行四边形。正方形两组对边分别平行，四个角都是直角，因此正方形也是特殊的平行四边形。而且正方形除了具备长方形的特点，还具有四条边相等这一特殊性质，因此正方形是特殊的长方形（如图4）。

教学中，笔者从平行四边形、长方形和正方形三者的异同点入手，精心设计问题引发学生思考，学生在分析和探究中主动把平行四边形的知识建构在长方形和正方形的知识基础上，从而实现了三者的有效联系和贯通，有利于学生从整体上学习知识，从而促进学生对知识的整体理解。

在教学“多边形的面积”时，笔者在学生掌握了平行四边形、三角形和梯形的面积公式后，引导学生发现它们之间的关系。笔者提出问题：“你能用梯形面积公式计算三角形和平行四边形的面积吗？”学生感到困惑，这三个图形的面积公式各不相同，怎么能用同一个公式计算呢？这个时候，笔者通过多媒体，演示梯形上底的两个端点逐渐靠近，最后重合成一个点，这样梯形就变成了三角形（把三角形看成是一个上底是0的特殊梯形）;梯形的下底逐渐缩短，上底逐渐变长，当上底和下底相等时，梯形就变成了平行四边形（把平行四边形看成是上底和下底相等的特殊梯形）。有了这样的铺垫，学生自然就能够理解梯形的面积公式同样适用于三角形和平行四边形，是一个“万能公式”。

教学中，教师创设问题情境，激发学生认知冲突，然后通过动态演示，有效地沟通了梯形、三角形和平行四边形之间的内在联系，使学生的视线不再局限于一个个具体的多边形，而是用更加宏观的视野对知识进行理解和定位，由此建构起多边形面积公式的知识体系，学生的思维自然也就会向更深处漫溯。

问题对学生的思维具有重要的催动和引发功能。在教学中，教师在设计问题时应明确问题的指向性，使问题设计更具针对性，以便更好地启迪学生思维，发展学生数学素养。

（责编 杨偲培）