基于光子轨道角动量的手性测量方法

胡海峰,詹其文

(上海理工大学光电信息与计算机工程学院,上海 200093)

0 引言

手性是指物体本身与其镜像不能重合的性质[1,2]。手性特征在自然界中普遍存在,也是自然界的一个基本属性。手性物体与其镜像被称为一对手性异构体。手性异构体的区分、识别和分离十分重要,例如在医药领域,手性相反的同分异构体可能具有完全不同的生物活性,甚至一种手性分子具有治疗效果,而具有相反手性的分子却会对人体产生毒性。由于它们的特性在很多方面都相同,如分子量、包含的原子种类、化学键、振动能级等物理与化学性质,因此只有当手性分子与其他带有手性特征的物质相互作用时才可能对其手性进行识别。光是具有手性的,典型的手性光为圆偏振光。手性分子对左旋和右旋圆偏振光的吸收效率存在差异,吸收效率的相对差别被定义为圆二色性(CD),其定义式为:g=2(A+-A-)/(A++A-),其中A+和A-分别是分子对左旋和右旋圆偏振光的吸收效率,而吸收效率定义为粒子吸收光能量与入射光能量的比值,该差别可以用非对称因子进行评价。通常来说手性分子的尺寸远远小于光学波长,这导致手性信号非常微弱[1]。为了提高手性信号的强度,哈佛大学Cohen教授课题组提出了光场手性概念[3],并从理论上证明了手性分子的圆二色信号与分子手性和光场手性均成正比。该课题组在实验上通过对光场的调控,可以在特定的空间位置产生比圆偏振光手性更强的超手性光场[4],进而实现CD信号的有效提升,由此开启了利用人工调控光场实现手性测量的研究。

左旋和右旋圆偏振光分别对应光子自旋量子数处于+1和-1的状态,因此光场手性与光子自旋角动量(SAM)密切相关。光子除了具有自旋角动量以外,还具有轨道角动量(OAM)。OAM光束是具有螺旋波前结构的一类特殊光束,近年来受到人们的广泛关注[5-8]。对OAM光束的系统研究开始于Allen等[9]的报道,他们发现对于近轴圆柱型光束,如果它的方位角相位满足eilφ(l为整数),就意味着在传播方向上每个光子具有lħ的OAM。根据手性在普遍意义上的定义,具有OAM的光束同样具有手性特征。由于近年来光场调控技术的不断发展[10],能否利用OAM光束测量物质手性并有效提高光学手性信号的强度受到了国内外相关领域研究人员的重视[11-14]。

本文对光子的自旋、轨道角动量和光场手性的概念进行了介绍,并在此基础上对现有基于OAM光束对分子进行手性测量的研究工作进行总结;对于手性颗粒尺寸较大,不满足Rayleigh条件的情况,介绍了Mie颗粒手性散射特性的计算方法,以及相关研究进展;最后对基于新型光子OAM态的手性测量研究进行了展望。

1 光子SAM、OAM与光场手性

光子的角动量由SAM和OAM两部分组成[15],由于光场中自旋-轨道耦合作用,使得在某些条件下两者之间可以相互转化[16]。在柱坐标系下,沿z方向传播的傍轴光束具有如下形式

式中:电场E为空间坐标(r,φ,z)和时间t的函数,k表示光波矢,ω表示光的圆频率。该光束的振幅分布函数u(r)具有轴对称特性,同时该光束还具有螺旋相位因子eilφ。定义轨道角动量z分量算符为:z=-i∂/∂φ,显然(1)式中的光束为z算符的本征态,本征值l即为光束携带的光子的轨道角动量量子数。常见的携带轨道角动量的光束包括拉盖尔-高斯光束和贝塞尔光束。该类光束的自旋角动量与偏振状态有关,将光场的偏振表示为其中σ为自旋角量子数。当σ=1时,对应左旋圆偏振光;而当σ=-1时,对应右旋圆偏振光。(1)式为傍轴近似下的光束表达式。对于非傍轴光束来说,其SAM和OAM的计算可参考相关文献[17]。

光场本身也可以具有手性,光场手性C可以用赝标量来进行描述[3],即

式中ε0和µ0分别为真空介电常数和真空磁导率。时谐形式下的电场E和磁场H 可以分别表示为和其中E和H是复数形式的电场和磁场分布。与电磁场能量守恒定理类似,可以写出光场手性守恒定理[3]

式中:F=[E×(∇×B)-B×(∇×E)]/2为手性流密度,B为磁感应强度,J为电流密度矢量。现有理论和实验工作表明光场手性可以用于增强手性分子的圆二色信号。假设分子的手征特性来源于电偶极子和磁偶极子之间的耦合效应,在分子为各向同性且尺寸远小于光波长的条件下,可以证明分子的圆二色信号与光场手性C成正比,因此如何实现光场手性的增强成为提高手性信号的重要目标之一。根据Harris等[18]的研究工作,不存在单一的手性参数能够普遍适用于评价所有物体的手性特征,因为对于任何一种测量方法,总能构造一个手性物体,使得测量得到的手性信号为0。除了电偶极子和磁偶极子之间的手性耦合效应之外,高阶极矩之间的耦合也能引起物体的光学手性信号。尤其是在物体尺寸达到波长量级的情况下,高阶极矩与光场之间的作用增强,在此情况下如何通过调控光场提高手性信号强度也是重要的研究方向,也使得光场OAM态在手性测量方面的应用成为可能。同时值得注意的是,在不考虑物质非线性光学响应的条件下,现有研究中得到的超手性光场在空间某个维度上都是局域化的。

2 基于OAM光束的手性测量研究现状

目前用于测量材料/结构手性的原理是基于被测样品对左旋和右旋圆偏振光响应的差异实现的,例如圆二色谱测量、偏振旋转测量等,这类手性信号是由光子的自旋角动量引起的。从光场的空间构型来看,无论是光子的自旋角动量还是轨道角动量都赋予了光场手性的特征。近年来,利用光场轨道角动量进行手性测量的研究工作逐渐受到研究人员的重视。相关研究可以分为两类:一种通过引入光子OAM态实现基于圆偏振光的CD测量信号的增强;另一种是通过改变入射光子OAM的符号,测量样品在相反OAM光子态激发下响应的差别,从而实现手性测量。为了将两种手性测量方法进行区分,可以将第二种测量称为OAM二色性。下面对这两种情况分别进行讨论。

2.1 光场OAM对CD测量的增强效应

传统CD信号的产生与圆偏振态(即光子的自旋)直接相关,而光子OAM态也可以激发分子的手性响应[11,13,14]。Babiker等[19]早期的理论研究表明电偶极跃迁机制无法与光场之间交换轨道角动量。该理论被Araoka等[20]的实验工作证实。但是通过OAM光束对结构中高阶极矩的激发作用,可以提高CD测量的信号强度。与手性分子相比,人工设计的结构具有更强的光学手性,最典型的例子就是金属螺旋结构。Reddy等[21]研究了同时具有SAM和OAM的复杂光子态与人工手性结构之间的相互作用,提出了波长可调的CD信号增强方法。对于非零阶的OAM光束,仅改变光子的自旋态,即测量所设计的手性结构在左旋光和右旋光照射条件下的吸收效率差别,得到CD信号,该信号可以通过提高光子的轨道角动量得到有效增强。理论上实现信号强度远高于传统CD测量的结果。

通常认为CD信号仅能在手性结构中产生,但是Zambrana-Puyalto等[22]报道了利用OAM光束激发亚波长金属圆孔结构获得80%～90%的CD信号。该结果表明对于非手性结构,采用OAM光束也可以激发CD信号。Wang等[23]对无手性的共轴纳米环表面等离激元结构的透射特性进行了研究,通过分析入射光束与结构中本征模式之间的耦合过程,证明了透射特性主要由光束的总角动量决定。同时,在透射过程中光场的总角动量是守恒的[23]。2017年,Afanasev等[24]理论上证明了当考虑分子高阶极矩的贡献时,带有OAM的入射光束可以激发非手性原子的CD信号。在上面提到的几项研究工作中,入射光束既具有SAM又具有OAM。当进行CD测量时,光束的OAM保持不变,同时使光束的偏振态在左旋圆偏振和右旋圆偏振之间切换。由于入射光束携带了OAM,左旋和右旋圆偏振态不再满足互为镜像的关系,并且两种状态具有的总角动量也存在差异,这种差异是非手性结构能产生CD信号的根本原因。为了具体说明该CD信号的成因,可以从近轴光束[如(1)式所示]出发进行分析[22]。当对(1)式中的光束进行围绕z轴的旋转操作后,得到的光束用Rz(θ)Eσ,l表示,其中σ为SAM量子数,l为OAM量子数。考虑到在Rz(θ)的作用下,用于表示光束偏振状态的矢量σ以及光束中的螺旋相位因子eilφ将做如下变化:因此,Rz(θ)Eσ,l=e-i(σ+l)θEσ,l,即近轴光束Eσ,l可看作算符Rz(θ)的本征态,对应的本征值为e-i(σ+l)。由于旋转算符与角动量算符之间具有如下关系:Rz(θ)=e-iJzθ,所以近轴光束也是z方向总角动量算符Jz的本征态,即JzEσ,l=(σ+l)Eσ,l,其中Jz的本征值为SAM量子数与OAM量子数之和。需要注意的是:当σ=0时,表示的是线偏振光束,不具备旋转不变性,因此也就不是Jz算符的本征态。另外,(1)式中的近轴光束还可以近似为螺旋度算符Λ=J·P/|P|的本征态,ΛEσ,l≈σEσ,l,其中P为线动量算符。因此对于左旋圆偏振态来说,螺旋度为+1,而对于右旋圆偏振态来说,螺旋度为-1,即光场螺旋度与自旋角动量相等,需要强调的是该结论仅适用于近轴光束。当镜像算符作用于Eσ,l时,可以得到

式中相位因子中的α取决于镜像算符的选择。(4)式说明当对近轴光束进行镜像操作时,OAM量子数、SAM量子数和螺旋度的符号均发生改变,其原因在于算符Jz和算符Λ都与镜像算符Mz满足反对易关系,即:JzMz=-MzJz,ΛMz=-MzΛ。对于文献[22]中研究的圆孔结构来说,由于圆孔具有旋转对称性和镜像对称性,因此透射场具有与入射场相同的SAM量子数和OAM量子数。基于该结论可以证明探测器在不同入射光条件下接收到的透射功率满足Iσ=1,l=Iσ=-1,-l,Iσ=1,-l=Iσ=-1,l。将金属圆孔的透射CD定义为当入射光束不具有OAM时(l=0),左旋圆偏振光和右旋圆偏振光的透射功率相等,即CD=0;当入射光束具有OAM时,由于透射功率依赖于入射光的总角动量,因此Iσ=1,l与Iσ=-1,l的值不相等,进而产生较强的CD信号。根据对称性关系可以证明:当OAM量子数改变符号时,CD信号的符号也将发生改变,即CDl=-CD-l。以上根据对称性推导出的结论与实验观测结果吻合。同样根据镜像变换方法,上面的测量也可以等价为固定圆偏振态(即光子SAM)不变的条件下,非手性样品在具有相反OAM的入射光束激发下的响应差别。因此这种非手性的CD信号可以用于入射光束总角动量的测量,同时也可以用于研究结构中高阶极矩与光束OAM之间的耦合机制。

2.2 基于OAM二色性的手性测量方法研究

从上面的讨论可以知道,手性信号的测量必须通过两束手性相反的光束分别激发样品,进而测量两次样品响应的差别,以完成信号的提取。这两次测量可以如上面提到的方法一样,仅改变光束的圆偏振态,即利用左旋光和右旋光分别作为光源进行测量;也可以通过改变入射光的螺旋形等相位面的方向(即光子OAM量子数的符号)实现结构手性特征的测量,即OAM二色性测量。2007年,Van Veenendaal和McNulty[25]理论上预测了X射线可以产生很强的OAM二色性。Forbes和Andrews[12]从量子理论出发,研究了分子与光子OAM的相互作用,结果表明电四极矩的贡献在分子与光子OAM手性相互作用中起到根本性作用。光子OAM引起的手性作用项源自电偶极矩和电四极矩之间的耦合效应[26],其耦合强度正比于入射光束的拓扑荷数。手性拉曼信号也是识别和分析手性分子振动能谱的有效工具。Forbes[27]在理论上提出对入射涡旋光的拓扑荷数符号敏感的手性拉曼机制,该机制同时也对入射圆偏振态的方向(即光子自旋符号)敏感,其中电四极矩跃迁机制也在手性拉曼过程中起到了重要作用。这些工作都为研究光子OAM与手性结构之间的相互作用提供了理论依据,基于这类相互作用有望发展新型的OAM二色性光谱测量技术,用于手性分子的精密识别和测量。

2016年,Brullot等[28]利用纳米颗粒聚集体结构中的电四极场局域增强效应,实现了手性分子的OAM二色性的测量(如图1所示)。由于电四极矩场导致的非对称透射,即透射强度与光传播的方向有关,对应的非对称透射系数AT为2(IfIb)/(If+Ib),其中If和Ib分别是正向传播和背向传播条件下的透射率。实验中分别对衬底结构、非手性样品以及加入L-苯丙氨酸和D-苯丙氨酸的样品的AT系数进行测量,入射光为800 nm的线偏振飞秒脉冲激光,并利用空间光调制器加载不同拓扑荷数的OAM光束,测量结果如图2所示。

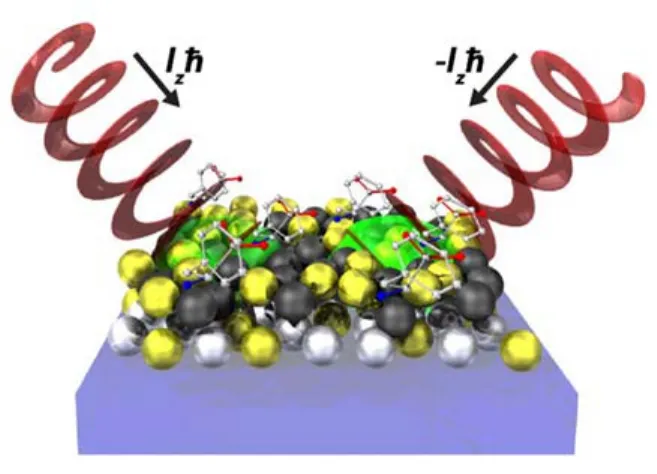
图1 基于纳米颗粒聚集体的电四极场局域增强效应实现利用带有轨道角动量的LG光束识别分子的手性[28]Fig.1 Optical OAM exhibited by twisted LG light can discriminate molecular enantiomers through the strong electric quadrupole fields generated in unique nanoparticle aggregates[28]

图2 带有OAM的入射光束造成的非对称透射现象[28]Fig.2 Asymmetric transmission as a function of OAM value of the light beam[28]

通过对比非手性的纳米聚体结构和衬底结构的非对称系数测量结果,可以证明光子OAM和纳米聚合体中的电四极场之间具有较强的相互作用,尤其是当入射光拓扑荷数增加时,非手性纳米聚合体的非对称系数显著增强。在纳米聚合体中加入L-苯丙氨酸和D-苯丙氨酸并进行非对称系数的测量,结果表明:当光子OAM为0时,对于两种苯丙氨酸的同分异构体来说,非对称系数基本没有差别;而当入射光子具有OAM时,非对称系数呈现出明显差别,从而证明了光子OAM与分子之间存在手性相互作用。

在紧聚焦条件下,光子的SAM和OAM会发生相互耦合,这种效应为基于光子OAM对局域光场手性的调控提供了理论基础。Wozniak等[29]研究了OAM光束的紧聚焦场与单个手性偶极散射体之间的相互作用,实验中利用电子束诱导沉积技术制备了亚波长尺度的手性螺旋,结构参数如图3(a)所示;利用NA=0.9的物镜对入射光进行聚焦,并利用NA=1.3的油浸物镜对透射光能量进行收集,如图3(b)所示。为了使入射光子只携带OAM而不具有SAM,该工作采用了携带拓扑荷为l=±1的线偏振拉盖尔-高斯光束作为入射光。根据螺旋结构的方向,紧聚焦光场中的纵向分量将有效激发z方向的电偶极子和磁偶极子,两者之间的振动相位延迟与入射光手性相匹配时,光场与手性结构之间的耦合强度增强,进而造成透射光强随入射光手性发生变化,如图3(c)所示。该工作从实验上验证了利用基于光子OAM实现手性测量的可行性。

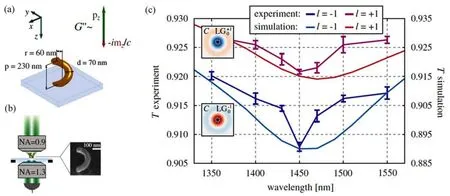
图3 (a)亚波长单螺旋结构示意图;(b)基于OAM紧聚焦光束的手性测量装置示意图;(c)相反OAM入射光束激发下实验测量和理论计算的纳米螺旋结构的透射光谱[29]Fig.3 (a)Structure of the subwavelength helix;(b)Sketch of the experimental setup for chirality measurement based on tightly focused OAM beams;(c)Experimental and simulation transimission spectra of the nanohelix under the incoming beams with opposite OAM[29]

近年来,研究人员提出了许多类型的纳米光学结构来增强手性信号强度[30-32]。当金属纳米结构与手性分子结构耦合作用很强时,会引起非手性金属结构中的手性吸收[33],因此利用近场增强结构与手性分子相结合是提升手性信号的有效方法。Wu等[34]提出同时利用远场光束OAM的调控和近场金属纳米颗粒结构实现手性信号的测量,该工作基于T-matrix方法对该结构中的散射特性进行了分析,其中金属纳米结构中表面等离激元共振效应增强了分子对入射光子OAM的手性响应。

2019年,Hu等[35]提出了基于OAM光束的紧聚焦超手性光场产生方法。图4为该方法中设计的紧聚焦光学系统原理图,入射径向偏振光经过螺旋相位板后成为携带OAM的光束。随后经过环形孔径后被高数值孔径物镜聚焦到衬底-空气界面,可以产生高度局域特性的超手性“光针”。基于Richards-Wolf矢量衍射积分公式可以对焦场进行计算,结果表明在聚焦透镜焦点位置处可以实现11.9倍于圆偏振光的光场手性增强效应,超手性增强针形区域的直径为λ/25,系统焦点附近的光场手性由入射光束的OAM符号决定。基于上述焦场计算的结果,进一步对高度局域的超手性光场的成因进行了分析,位于焦点处的手性分子对光的吸收分为纯电偶极吸收和电偶-磁偶混合吸收两部分。其中纯电偶极吸收与入射光手性无关,主要与电场Ez分量相关;电偶-磁偶混合吸收贡献依赖于入射光手性,与电场和磁场在xy平面内的切向分量E‖和H‖相关。由于电场Ez分量在光束中心存在相位奇点,抑制了光束中心的非手性吸收,最终形成了深亚波长超手性光场。在该结构中,可以通过在衬底-空气界面引入布拉格光栅以进一步提高光场的手性[36]。

图4 (a)基于紧聚焦涡旋径向偏振光束的超手性光场产生系统;(b)焦场计算理论模型[35]Fig.4 (a)Schematic of the system to generate a superchiral field by focusing a twisted radially polarized(RP)beam;(b)Theoretical model to calculate the EM field distribution near the focus[35]

由于在入瞳平面对入射光进行了环形空间滤波,极大地压缩了聚焦光束的角谱分布,使得产生的超手性光束具有近似于无衍射贝塞尔光束的特性。这种光场特性有利于实现样品手性特征的高空间分辨率二维扫描成像。值得注意的是,该工作中光场手性的根源是光子的OAM态,但是在紧聚焦过程中存在光子的自旋-轨道耦合效应,实际上聚焦场中实现了光子自旋态对激发分子超手性响应起到关键作用。该过程可以通过Richards-Wolf矢量衍射积分公式进行分析和说明:考虑一束同时具有径向偏振特性和螺旋相位因子的贝塞尔-高斯光束被高数值孔径的物镜聚焦,在正弦条件下物镜的切趾函数可以表示为

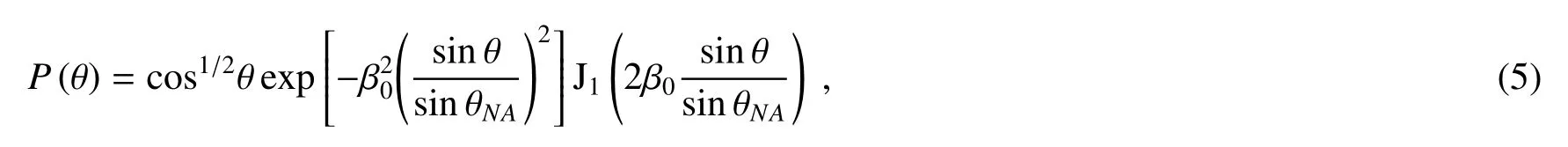
式中:θ为透射光线的偏转角度;β0=(f/w0)sinθNA,其中f为物镜焦距,w0为入射光束的束腰,θNA表示数值孔径角;J1为一阶Bessel函数。当入射光束的OAM量子数为l时,焦点附近(ρ,φ,z)点处的电场和磁场的表达式为

式中:Z0表示真空阻抗,函数Fs、Fc和F1分别定义为

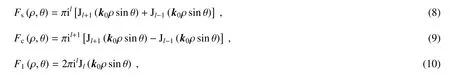
式中:Jl(x)表示l阶贝塞尔函数,k0为真空波矢。(6)、(7)式中的积分范围可以通过物镜前的环形孔径光阑进行调控(如图4所示)。当l=±1,且仅有θ=θ0孔径带上的光能通过时,焦点位置(即ρ=0,z=0)的电场和磁场可以简化为

可见焦点处的光场为圆偏振态,通过改变入射光束OAM量子数的符号可以实现左旋圆偏振和右旋圆偏振状态之间的切换。因此通过对入射光束的紧聚焦,完成了入射光束的OAM向汇聚焦点处的SAM态的转化。同时电场和磁场之间的比值为|E|/|H|=Z0cosθ0。与平面波相比,磁场分量的振幅增强了1/cosθ0,从而提高了手性吸收能量在总吸收能量中的比值。因此,焦点位置光场的手性来源于入射光束的OAM。同样,从光子自旋-轨道相互作用的角度出发,经过适当的光学偏振调制结构,可以利用圆偏振光入射激发系统中超手性光场,如图5(b)所示,这意味着该方法很大程度上也可以与传统CD测量方法兼容。

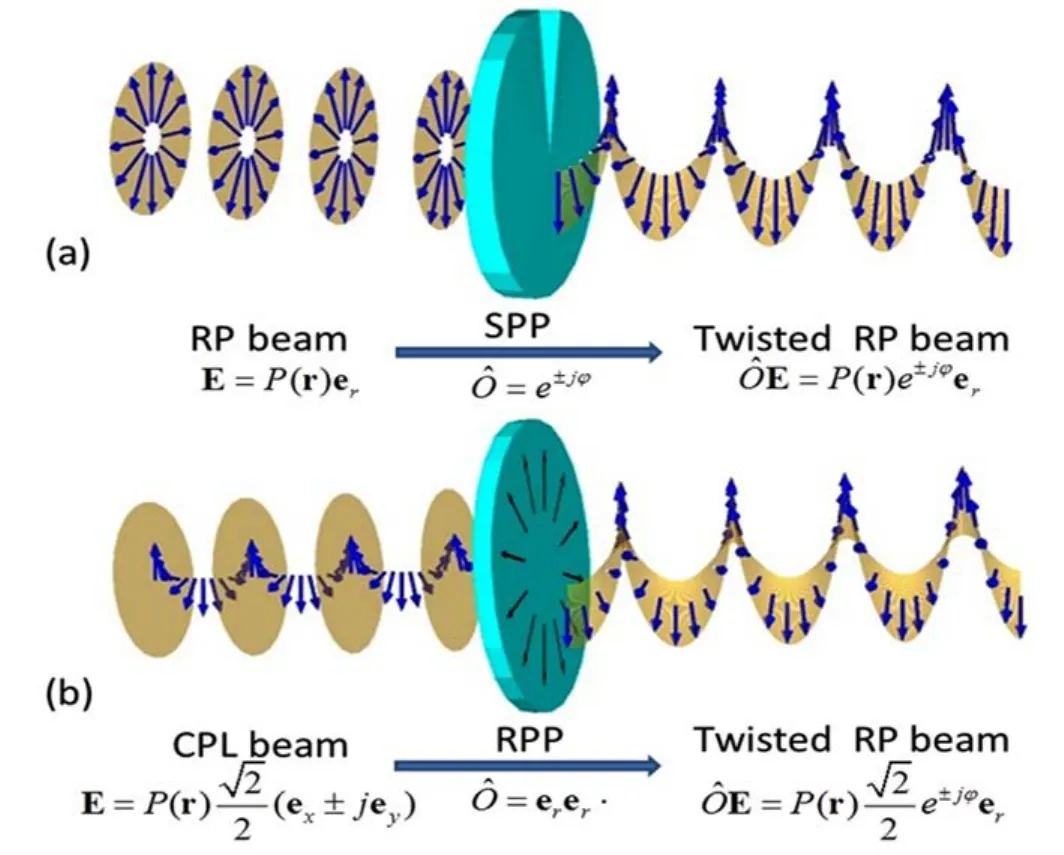
图5 (a)径向偏振光束经过螺旋相位板产生带有OAM的径向偏振光;(b)圆偏振光经过径向偏振片产生带有OAM的径向偏振光[35]Fig.5 (a)The twisted RP beam converted by RP beam passing through spiral phase plate;(b)The twisted RP beam converted by circularly polarized light(CPL)beam passing through radially polarized plate[35]

3 Mie颗粒的手性信号增强

现有研究工作中,为了增强分子手性信号,采用的主要方案是通过近场微纳结构的设计或者对入射光场的调控实现手性分子所在位置光场手性的局域增强。该方案对于尺寸远小于波长的Rayleigh颗粒来说,可以有效提升手性信号。对于Rayleigh颗粒,其散射光的强度与入射光的波长四次方成反比,但是随着颗粒尺寸的增加,其散射特性无法利用Rayleigh散射模型描述,需要引入Mie散射模型对散射光场进行计算。Mie颗粒的光学手性特征与其对光的散射效应紧密联系,手性信号的强度不仅受到入射光场特性的影响,同时也和颗粒的尺寸、形状等结构参数密切相关。这与Rayleigh颗粒的手性散射特性存在显著不同,因此本部分将对Mie颗粒手性信号增强方面的研究进行介绍。对于球形手性Mie颗粒散射特性的计算,T矩阵方法较其他数值方法(如FDTD和FEM等)具有明显的优势[37]。为了分析基于OAM的超手性紧聚焦光场对手性颗粒散射信号的增强效果,可以借助下面的理论模型进行分析。基于手性材料的本构关系[38]

该材料同时满足互易性条件,其中ε1和µ1为构成小球的手性材料的介电常数和磁导率,κ1为手性参数,用来描述材料光学手性的强弱。基于Lorenz-Mie理论,入射场可以展开为矢量球谐函数的线性组合

式中:k0为入射光的真空波矢;Z0为真空阻抗;RgMmn和RgNmn用来表示无奇点的矢量球谐函数,m和n用来表示矢量球谐函数的阶数;umn和νmn是相应的展开系数,系数具体取值可由具体入射场的形式确定。同理,散射场也可以表示成(15)、(16)式的形式,具体展开式可表示为

与入射场不同,散射场应该利用坐标原点带有奇点的矢量球谐函数Mmn和Nmn进行展开,其展开系数为amn和bmn。这类矢量球谐函数在远场仅包含向外辐射的球面波成分。利用T矩阵可以建立入射场的展开系数和散射场的展开系数之间的数学关系,可表示为

有关颗粒T矩阵的计算方法可以参考相关的专著[37],对于手性球形颗粒的T矩阵可以参考Bohren的工作[39]。基于该方法,将文献[35]中提出的基于紧聚焦系统的超手性光场用于测量手性球形颗粒的散射CD信号[40],如图6(a)所示。在计算模型中小球直径为150 nm,介电常数为25,磁导率为1,手性参数为0.01。在圆偏振光入射条件下,散射CD光谱如图6(a)中的红色曲线所示;采用文献[35]中提出的局域超手性光场作为激发光进行仿真,得到散射CD光谱如黑色曲线所示。通过比较发现,圆偏振光条件下得到的最大散射CD信号为0.0303,而超手性光场条件下得到的最大散射CD信号为0.0445。采用超手性光场作为入射场对Mie颗粒的CD信号的提高能力有限。通过改变超手性光场的入射条件,分析在不同入射角度的条件下散射CD信号的增强效果,结果发现当入射角度接近全反射临界角时,散射CD信号将出现急剧下降[图6(b)],因此超手性光场增强散射CD信号需要选择合适的入射角度。

图6 (a)圆偏振光和局域超手性光激发下的散射CD光谱,插图为手性球形颗粒在超手性光场中的散射分析模型;(b)不同聚焦条件下手性光谱的峰值曲线[40]Fig.6 (a)The scattering CD under the incidence of CPL(red curve)and local superchiral field(black curve).The inset shows the model to analysis the light scattering by the sphere in superchiral field;(b)The peak value of scattering CD spectra with different focusing condition[40]

通过上面的分析可知,当手性颗粒尺寸增大,不满足Rayleigh散射条件时,很难仅通过提升光场手性来实现手性信号的增强。而目前对Mie颗粒的手性信号增强尚未建立完善的理论。但是相关研究工作表明,采用具有高阶轨道角动量的聚焦光束对于提高大尺寸手性颗粒的散射信号是十分有效的。Ni等[41]对于结构尺寸远大于波长的人工结构的OAM二色性进行了研究。实验上基于飞秒激光加工技术,制备了直径为17.4µm、高度为21.4µm的三维螺旋结构,其左旋结构和右旋结构如图7(a)、(b)所示;为了方便进行对比,该光场同时制备了无手性的圆盘结构,如图7(c)所示。在测量系统中,通过空间光调制器产生不同阶的OAM光束,其拓扑荷的变化范围在-75～75之间。通过测量手性结构对OAM的散射得到图7(a)～(c)中散射功率与光束拓扑荷之间的关系曲线,结果表明手性结构对相反拓扑荷的光束的散射效率具有显著差别。图7(a)～(c)中所示三种结构的OAM二色谱如图7(d)所示,对于人工加工的螺旋结构来说,OAM二色性值最大可达到120%(理论极限值为200%)。该工作展示了光子OAM态可实现大尺寸手性颗粒的超强光学手性信号。

图7 不同拓扑荷数条件下三种不同结构的散射强度(a)左旋结构,(b)右旋结构,(c)非手性结构;(d)三种结构的OAM二色谱[41]Fig.7 The scattering intensities for three different structures illuminated by optical vortices with different topological charges.(a)Left-handed structure,(b)Right-handed structure,(c)Achiral microstructures;(d)The OAM-induced dichroism for the three structures[41]

4 总结与展望

综上所述,对光子OAM态的研究工作极大丰富了光学手性的研究领域,利用OAM光束增强手性物体光学信号在某些特定结构中已经展现出显著的优势。除了OAM态以外,近期相关工作表明利用柱矢量光束也可以实现手性信号的增强[42,43]。对于尺寸较小的Rayleigh颗粒,光场局域手性强度与颗粒产生的手性信号直接相关。但是手性信号的产生依赖于电偶极矩和高阶极矩(如磁偶极矩)之间的耦合效应。因此颗粒对入射光的吸收或散射效率存在限制。Ayuso等[44]基于对超短脉冲在时间和空间上的调控技术提出了一种新型手性光场,并构建了光场手性度的概念。Neufeld等[45]在理论上构建了手性度为69.6%的手性光场,为超手性光场的设计提供了新的路线。值得注意的是,近期光场时空调控技术取得了很大的进展,Chong等[46]基于光场时空调控的新方法,采用二维时空波前整形成功产生了具有可控横向OAM的时空涡旋。有关该领域的研究目前正在不断深入[47-49]。从横向OAM时空涡旋具有的螺旋相位结构来看,该光场与其自身的镜像光场不能重合,说明时空涡旋光场具有手性特征。未来该光场有望用于物质结构手性测量方面的研究工作,但是如何利用横向OAM引起的光场手性实现对物质结构手性的识别和测量尚有待研究。另一方面,对于尺寸较大的颗粒,由于内部高阶极矩的激发以及不同阶极矩之间的相互作用,使得单纯考虑低阶偶极矩难以完成针对Mie颗粒的手性光场设计。目前针对大尺寸颗粒与结构仍需要系统化理论和实验研究,以便实现多极矩共存条件下手性光学信号的增强。