压缩混沌光场的量子统计性质研究

万志龙,李恒梅,王震,王刚，黄红云

(常州工学院数理与化工学院,江苏常州213032)

压缩混沌光场的量子统计性质研究

万志龙,李恒梅,王震,王刚，黄红云

(常州工学院数理与化工学院,江苏常州213032)

研究压缩混沌光场的量子统计性质。压缩混沌光场在动量P分量上具有明显的压缩效应，并呈现光子聚束和超泊松分布等特性。光场的压缩效应越强，平均光子数、光子数涨落就越大。在相空间中光场的Wigner函数为高斯态分布，且不存在负部区域。

压缩混沌光场；正规乘积；Wigner函数

混沌光场(也称热态光场)是一种典型的高斯态光场。混沌光场经压缩后也可以看成一般意义下的高斯态光场，近十几年来这方面的研究逐渐成为热点[1-2]。文献[3]在理论上研究了单模压缩混沌光场和平移压缩混沌光场的位相；文献[4—5]对压缩混沌光场中某些态的非经典特性进行了研究。对于高斯态压缩光场，人们提出了一些测量光场的压缩、纯度及纠缠度的实验方案[6-7]。本文利用有序算符内的积分技术研究了压缩混沌光场的量子统计性质。

1 压缩混沌光场ρS的正规乘积形式

将单模压缩算符[8]S(r)作用于混沌光场的密度算符ρc=(1-e-λ)e-λa+a，可得到压缩混沌光场的密度算符ρS，

ρS=S(r)ρcS-1(r)= (1-e-λ)S(r)e-λa+aS-1(r)

(1)

SPS-1=erP,SQS-1=e-rQ

(2)

利用算符恒等式

(3)

以及压缩变换关系(2)和Weyl编序算符在相似变换下的不变性[9]，可得到压缩混沌光场ρS的正规乘积形式

(4)

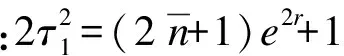
2 压缩混沌光场的量子统计性质

2.1Mandel-Q参数

该参数最早由Mandel[10]引入，用于描述光场的光子数分布偏离泊松统计分布的程度。由式(4)不难得到平均光子数〈a+a〉和〈a+2a2〉

(5)

于是，Mandel-Q参数为

(6)

进一步可得光子数涨落为

(7)

从式(5)～(7)可知，光场的光子数分布为超泊松分布，且光场受到的压缩越强，平均光子数和光子数涨落就越大，这是压缩混沌光场的新特性。

2.2二阶相干度

(8)

显然，当r→0，光场的压缩为零，压缩混沌光场退化为混沌光场，根据式(8)可计算出二阶相干度g(2)=2，因此混沌光场是聚束的。而当其被压缩后，二阶相干度g(2)>2，故压缩混沌光场仍是聚束的，这表明混沌光场在被压缩前后始终保持经典特性。

2.3光子数分布

(9)

图1(a)和(b)分别给出了对于不同压缩参数r的光子数分布。由图可知，随着压缩参数r的增加，光子数分布主体向更大光子数方向移动。

(a)r=0.1

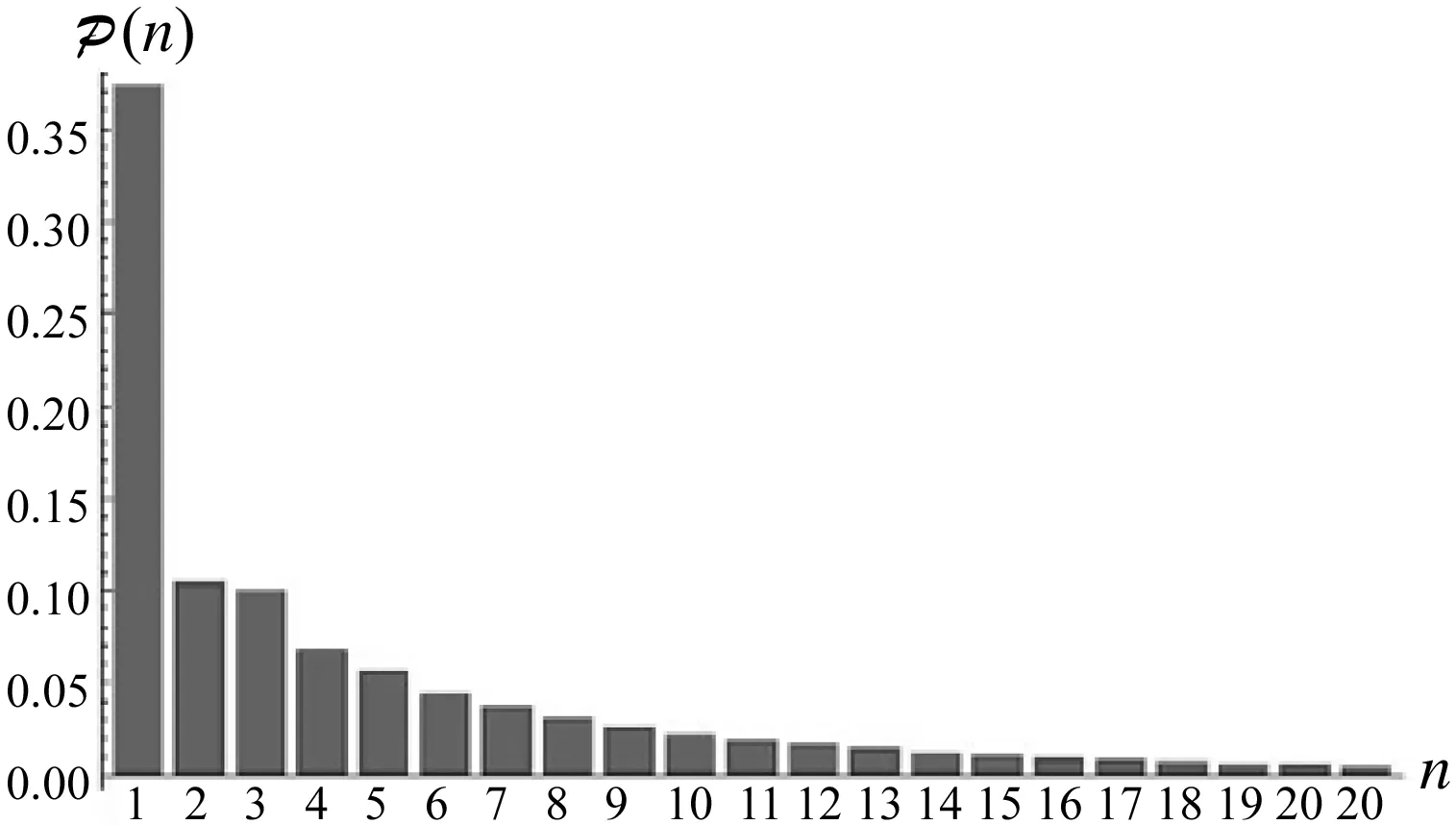
(b)r=0.9图1 压缩混沌光场的光子数分布=1)

2.4Wigner函数

在量子统计物理中，Wigner函数能反映量子态在相空间演化过程中的所有信息，是重要的准概率分布函数。同时Wigner函数的负值也是反映光场非经典性质的一个重要标志。利用Wigner函数在相干态表象中的一般表达式[12]

(10)

结合式(4)，可导出压缩混沌光场的Wigner函数

(11)

特别地，当r→0，光场压缩为零，根据前面给出的条件，上式退化为混沌光场的Wigner函数

(12)

利用压缩混沌光场Wigner函数的解析式(11)，对于不同参数r，绘制Wigner函数分布，如图2(a)和(b)。由图可知，位相空间中的Wigner函数分布属于高斯态分布；光场在某一正交分量上存在明显的压缩效应，且随着参数r的增大，压缩效应增强,但是Wigner函数不存在负部区域。

(a)r=0.4

(b)r=0.8图2压缩混沌光场的Wigner分布函数(n=0.1)

3 结论

利用有序算符内的积分技术，结合Weyl编序下相似变换不变性，推导出了压缩混沌光场密度算符的正规乘积形式，进一步研究了压缩混沌光场的量子统计性质，如Mandel-Q参数、二阶相干度、光子数分布、Wigner函数等。结果表明，压缩混沌光场在动量P分量上具有明显的压缩效应，并呈现光子聚束和超泊松分布等特性。光场的压缩效应越强，平均光子数、光子数涨落就越大，光子数分布主体向更大光子数方向移动。光场的Wigner函数为高斯态分布，且不存在负部区域。压缩混沌光场的这些量子特性不但丰富了量子力学和量子光学理论基础，同时也为压缩态光场在量子通信、量子计算机等技术上的应用提供了理论参考。如果对混沌光场继续进行非高斯操作，可得到一系列的非高斯量子态，它们会呈现不同的量子统计特性，这也是接下来要开展的课题。

[1]WENGER J,FIURASEK J,TUALLE-BROURI R,et al.Pulsed squeezed vacuum characterization without homodyning[J].Phys Rev A,2004,70(5):053812.

[2]HU L Y,FAN H Y.Wigner functions of thermo number state,photon subtracted and added thermo vacuum state at finite temperature[J].Mod Phys Lett A,2009,24(28):2263-2274.

[3]ASPACHS M,CALSAMINGLIA J,MUNZ-TAPIA R,et al.Phase estimation for thermal Gaussian states[J].Phys Rev A,2009,79(3):033834.

[4]KIM M S,BUZEK V.Photon statistics of superposition states in phase-sensitive reservoirs[J].Phys Rev A,1993,47(1):610.

[5]PHOENIX S J D.Wave-packet evolution in the damped oscillator[J].Phys Rev A,1990,41(9):5132.

[6]MARIAN P,MARIAN T A.Squeezed states with thermal noise.1.Photon-number statistics[J].Phys Rev A,1993,47(5):4474.

[7]FIURASEK J,CERF N J.How to measure squeezing and entanglement of Gaussian states without homodyning[J].Phys Rev Lett,2004,93(6):063601.

[8]范洪义,袁洪春.从相干态到压缩态[M].合肥:中国科学技术大学出版社，2012.

[9]范洪义.量子力学表象与变换论—狄拉克符号法进阶[M].2版.合肥:中国科学技术大学出版社,2012:12.

[10]MANDEL L.Sub-Poissonian photon statistics in resonance fluorescence[J].Opt Lett,1979，4(7)：205-207.

[11]SPAELTER S,BURK M,STROESSNER U,et al.Propagation of quantum properties of sub-picosecond solitons in a fiber[J].Opt Express,1998,2(3):77-83.

[12]FAN H Y,ZAIDI H R.Application of IWOP technique to the generalized Weyl correspondence[J].Phys Lett A,1987,124 (6):305.

责任编辑：杨子立

QuantumStatisticPropertiesoftheSqueezedChaoticLight

WANZhilong,LIHengmei,WANGZhen,WANGGang,HUANGHongyun

(School of Sciences and Chemical Engineering,Changzhou Institute of Technology,Changzhou 213032)

Quantum statistical properties of squeezed chaotic light was investigated.The results showed that squeezing effect in momentumPis clear and it brings bunching effect and Super-Poisson distribution.For the chaotic state,the stronger the squeezing is,the larger the photon number average and fluctuation is.Wigner function is also analytically derived.It can be found that Wigner function is Gaussian in phase space,and there is no negative region.

squeezed chaotic light;normal ordering;Wigner function

10.3969/j.issn.1671- 0436.2017.03.009

2017- 05- 09

江苏省教育厅高校自然科学研究面上项目(16KJB140001)；常州工学院科研基金项目(YN1630)

万志龙(1981— )，男，博士，讲师。

O431.2

：A

：1671- 0436(2017)03- 0041- 03