对经典力学中的轨道角动量和自转角动量的探讨
2022-09-15林正喆
林正喆,陈 熙
(西安电子科技大学 物理与光电工程学院,陕西 西安 710071)
通常在量子力学教科书中对自旋角动量的规范的说法是:自旋角动量是量子力学中的一个新的自由度,没有经典对应[1-6]. 把自旋归结为经典的转动是不合适的.实际上,经典力学中存在轨道角动量和自转角动量的概念. 对具有几何形状的物体的空间运动,轨道角动量指的是其质心运动的角动量,自转角动量指的是其绕自身质心旋转的角动量.我们有必要在经典力学中建立两种角动量的严格理论,并对一些实际的体系进行研究.本文试图阐述经典力学中的轨道角动量和自转角动量的严格理论框架,并通过一些例子总结出完善的经典力学角动量理论.
1 经典力学中的轨道角动量和自转角动量
在力学中,先对单个质点的角动量进行定义,而后给出质点系的总角动量.在惯性系中,质点系相对于坐标原点O的总角动量为
(1)
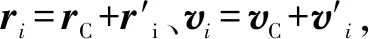
(2)
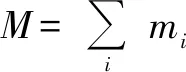
(3)
其中第1项表示系统质心绕坐标原点运动的角动量,称作轨道角动量.第2项为系统内各个质点相对于质心的角动量之和,与系统绕其质心的运动有关,称为自转角动量.该式对惯性系中任意质点系的运动成立,可应用于刚体力学.该式给出了与量子力学中角动量类似的形式,将总角动量分解为轨道角动量与自转角动量的和.

图1 质点的位置和速度相对于质心坐标系的分解
2 总角动量分解的应用意义
对刚体的一般运动,通过将体系的运动分解为质心的平动和绕质心的转动两部分进行分析.设第i个质点受到的合外力为Fi,按质心运动定理有
(4)
对系统绕质心的转动,按质心系角动量定理有
(5)
对于刚体,将式(5)中的绕质心角动量用转动惯量张量和角速度矢量表达之后,这两个式子构成可完备求解的方程组.对系统的总角动量式(3)运用角动量定理则有
(6)

3 轨道角动量和自转角动量在力学问题中的应用
3.1 重对称陀螺的运动
下面利用轨道角动量和自转角动量的概念,建立对重对称陀螺运动的一种描述方法.如图2所示,质量为m,O点与地面相接触的重对称陀螺.C为其质心.以O点为坐标原点,质心位置为rC.陀螺以角速度ω绕其对称轴自转,自转轴与z轴夹角为θ.陀螺绕z轴进动的角速度为Ω.
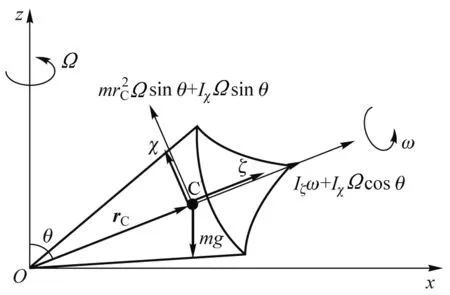
图2 重对称陀螺
为了描述角动量,在陀螺质心C上建立χ-ζ坐标系(图2).其中ζ沿陀螺对称轴方向.陀螺质心C绕O点的轨道角动量为
(7)
陀螺的自转为两种转动的合成,其一是自身以角速度ω绕ζ轴的旋转,其二是进动引起的以角速度Ω绕z轴的旋转.由于对称性,χ、ζ轴为陀螺的惯性主轴.陀螺的自转角动量为
Ls=Iζ(ω+Ωcosθ)eζ+IχΩsinθeχ
(8)
总角动量L=Lo+Ls的水平分量(沿x轴)为
Lx=Iζ(ω+Ωcosθ)sinθ-
(9)
重力对O点力矩为mgrCsinθ.若陀螺处在稳定的(无章动)进动状态,则根据角动量定理mgrCsinθ=ΩLx得
(10)
式(10)的解为无章动进动Ω所需满足的条件.若Ω小于该方程的解,则陀螺自转轴向下运动以补偿不足的角动量变化率dL/dt,同时Lx增大.Lx增大到一定程度以后将遏制陀螺自转轴的向下运动,并反过来朝上运动.此过程反复,形成章动.
通过重对称陀螺模型,可使学生深入理解经典力学中的轨道角动量与自转角动量概念.在日后学习量子力学时,学生将经典力学的自转角动量和量子力学中的自旋角动量概念相互比较,认识其异同.在经典力学中建立轨道角动量与自转角动量概念,使其理论构架更加完善,并使学生对角动量建立全面的认识.
3.2 两个边缘相接触的转盘
如图3所示,将两个正在旋转的、半径分别为R和r旋转的转盘边缘相互接触,二者发生摩擦,在经过一段时间后达到稳定运动状态.设二者均为均质圆盘,质量分别为M和m,初始角速度为Ω0和ω0,不计两个轮轴的摩擦,计算达到稳定运动状态后二者的角速度.
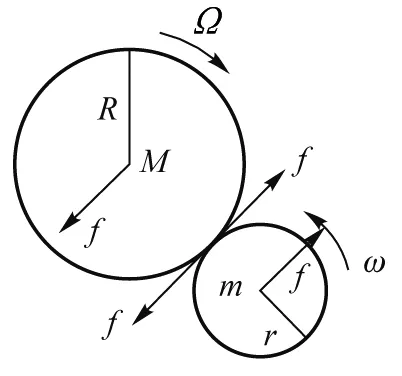
图3 两个边缘相互接触的转盘
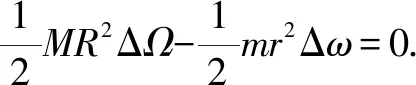
(11)
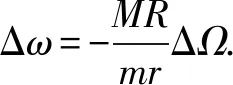
(12)
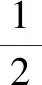
(13)
可根据式(11)验证式(13)成立.虽然式(13)不足以用来求解体系运动过程,但通过以上讨论可加深对力学中角动量原理的理解.
3.3 平行轴定理
刚体转动惯量的平行轴定理也是与总角动量分解相关联的一个例子.如图4所示,一个质量为m、绕O轴旋转角速度为ω的刚体,设C为其质心、OC两轴距离为d,则刚体绕O轴的总角动量可分解为
L=mωd2+ICω
(14)
其中第1项为质心绕O轴的轨道角动量,第2项为刚体绕其质心的自转角动量,IC为绕C轴的转动惯量.设L=Iω,则可得刚体绕O轴的转动惯量为
I=IC+md2
(15)
即平行轴定理.由此可看到,总角动量的分解自然地与平行轴定理相自洽.
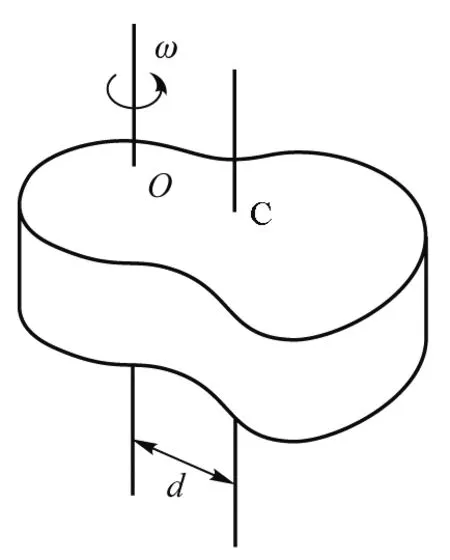
图4 绕O轴旋转的刚体,C为其质心
4 结论
轨道角动量和自转角动量的概念可从经典力学中得到.事实上,在人们建立量子力学自旋概念的过程中,借助了经典的自转角动量概念.角动量作为力学中的重要概念,有必要对其进行深入的理论阐述.本文建立了经典力学中质点系的轨道角动量和自转角动量的概念,使经典力学的理论体系更加完备.
