基于光学衍射神经网络的完美涡旋光轨道角动量识别

成科,胡晓楠,贺瑜,孟维佳,栾海涛,顾敏,方心远∗

(1上海理工大学光子芯片研究院,上海 200093;2上海理工大学光电信息与计算机工程学院人工智能纳米光子学中心,上海 200093)

0 引言

1992年,Allen等[1]发现具有螺旋相位[exp(iℓφ),其中的ℓ与φ分别代表拓扑荷(TC)与柱坐标系下的方位角]的涡旋光束可以携带ℓħ的轨道角动量(OAM)。其中,作为一类特殊的OAM光束,完美涡旋光束(POVB)的振幅分布与拓扑电荷ℓ无关[2],其电场表达式为EPOVB=δ(r-r0)exp(iℓφ),r0表示设定的POVB半径。目前,POVB的主要产生方法包括利用拉盖尔-高斯光束照射轴棱镜[3,4],在数字微镜阵列(DMD)加载二元振幅型全息图[5]或者在空间光调制器(SLM)上加载连续相位型全息图的全息法[6-9]以及使用几何相位液晶元件[10,11]产生连续相位等。POVB在粒子捕获[12]、超分辨成像[13]、光通信[14]等领域拥有广阔的应用前景。此外,POVB散射场的无衍射特性在成像和密码学方面具有潜在的用途[15]。

探测OAM状态是研究POVB的一项重要任务。2017年,Ma等[16]利用相移技术,通过计算干涉条纹的数量来确定POVB的TC。2020年,Ding等[17]将椭圆艾里相位嵌入到涡旋光束的产生装置中,通过分析远场衍射图样实现了POVB中TC的探测。2020年,Chu等[18]利用混合角梯度相位光栅确定入射POVB的TC。利用空间光调制器代替球形双凸透镜[19]或者锥透镜[20],可以直接根据POVB光束的光场分布计算出实现OAM状态的探测。近期,根据涡旋光束的强度分布与其OAM相关的这一物理特性,研究人员利用人工智能(AI)算法探测涡旋光束的OAM状态。2014年,Krenn等[21]首次使用人工神经网络(ANN)进行OAM模式识别。2017年,研究人员基于卷积神经网络(CNN)在处理图像分类问题上的优势,实现了准确率高于99%的OAM模式识别[22,23]。但是,不同OAM阶数的POVB理论上拥有完全相同的光强分布,因此无法将CNN应用于POVB轨道角动量的探测。

最近出现了一类以光作为信息的载体,基于衍射实现神经元链接的光学衍射神经网络(DNN)[24],与电学CNN相比,DNN能够同时处理振幅和相位,为涡旋光束的OAM探测提供了新的思路。在传统的干涉测量检测OAM[25,26]的方法当中,实际应用时不可避免的大气湍流、光路准直等问题将影响OAM分类的效果,而神经网络在学习过程中可以将各种各样外在的影响因素考虑在内[27-29]。因此本文采用DNN对POVB的拓扑荷进行识别,并在实验上实现了密集间隔(Δℓ=1)与高阶OAM状态(ℓ=-50～+50)的POVB识别,进一步研究了分数阶、整数阶叠加态OAM的POVB探测识别。此外,还考虑了在大气湍流和光路准直的影响下,构建DNN探测POVB的OAM状态,确保DNN在多种环境下对OAM探测的正确率。本文的研究内容可能为OAM通信和全光信息处理等领域提供新的思路。

1 实验方案与装置

1.1 DNN模型的设计原理

基于DNN分类POVB拓扑荷的概念图如图1所示。DNN由若干透射(或反射)层组成,其中的每个像素充当神经元,具有复数值透射(或反射)系数。通过学习,在网络的输入和输出平面之间执行函数可以训练每一层的透射或反射系数[图1(a)]。在本研究提出的实验设计中,网络的输入层为POVB的复振幅信息,隐藏层由经过训练后的一个纯相位衍射层充当,最后对数据标签进行处理,设计不同位置的光强分布作为网络的输出层,判断输出层图像中光强最大的区域即可得到结果图像所表征的标签[图1(b)]。

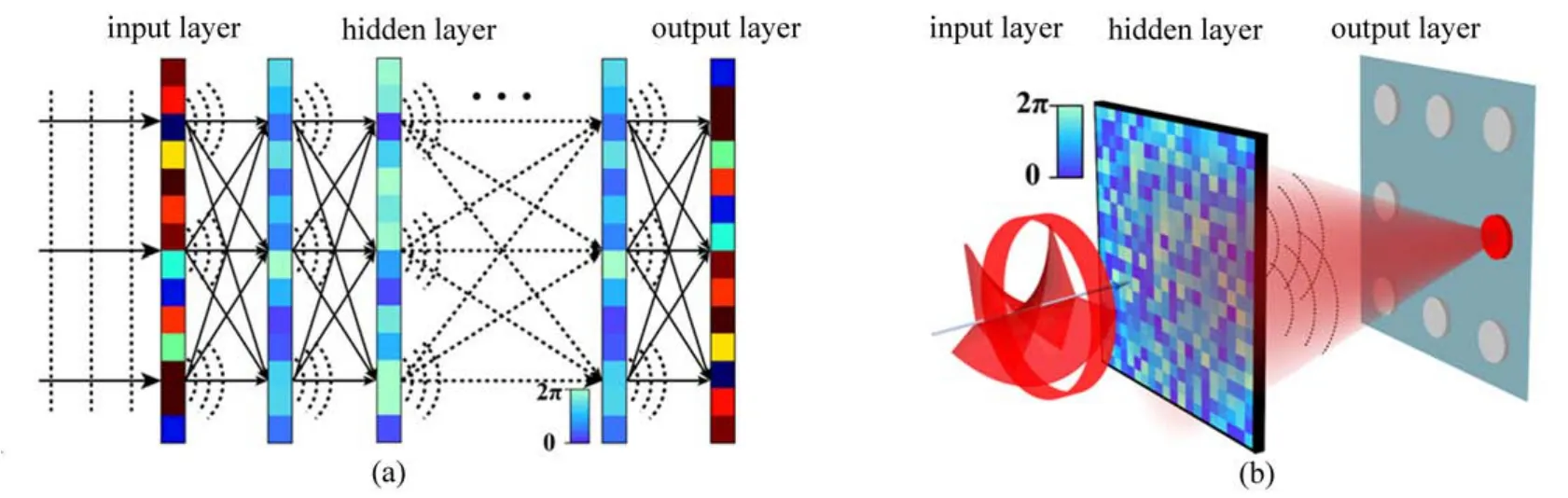
图1 基于DNN的POVB识别。(a)DNN模型;(b)基于DNN分类POVB概念图Fig.1 Recognition of POVB based on DNN.(a)DNN model;(b)Conceptual illustration of DNN for POVB recognition

DNN的设计和训练过程如图2(a)所示,建模过程主要运用了角谱传输理论以及梯度下降算法。首先,将光束的复振幅场作为DNN网络的输入层,通过角谱衍射自由传播到第一层,经过相位调制再角谱衍射到下一层,在最后的输出层中将光强与标签真值进行均方差以计算损失函数,利用随机梯度下降算法进行网络损失函数的下降,降至所需阈值或者达到迭代次数,随后网络将优化DNN的变量参数,即相位变量层,再通过激活函数实现最终的复振幅场调制,并在迭代过程中不断优化以达到最终的目的。

图2 DNN分类POVBs的算法设计。(a)算法设计流程图;(b)DNN各层的振幅和相位;(c)训练过程中的损失函数值变化曲线Fig.2 Design of DNN for the classification of POVBs.(a)Flow chart of proposed algorithm;(b)Amplitude and phase distributions of each layer of DNN;(c)Variation curve of loss function value during training

根据Rayleigh-Sommerfeld原理,网络上的每一个单元都可视为下一层网络的入射源,可表达为

式中:A为第i个神经元输出的幅度因子,Δθ为输入光波在i处叠加产生的相位延迟因子,并令∑ ,表示第q层网络的第i个神经元的输入。神经元的传输系数可以表达为

式中K表示输出平面的测量点数。DNN设计的优化可以转化为在的范围内求取

应用误差反向传播训练DNN,需要计算损失函数对所有网络变量的梯度。损失函数对第q层的误差梯度表达式为

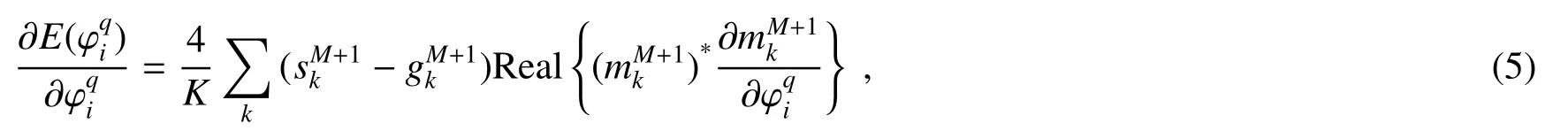
式中3≤Q≤M-1。在推导这些偏导数时,值得注意的是,对于q≤M层的任意神经元,可以表示为

式中k1、k2表示虚拟变量。在误差反向传播的每次迭代过程中,将少量的训练数据输入到衍射神经网络中,计算每个层的上述梯度,并相应地更新DNN。

如图2(b)所示,本研究将携带振幅和相位信息的POVB作为输入信息进入隐藏层,相位调制后通过角谱衍射到达输出层,网络输出的光场强度与目标区域的能量或光强进行均方差运算,然后对其数值进行梯度下降,作为训练POVB分类DNN的损失函数,并更新迭代隐藏层,这里选择迭代次数作为限制,训练过程的损失函数值变化曲线如图2(c)所示,经过5000次迭代,最终输出训练后隐藏层相位分布图像。

1.2 POVB的产生及实验装置

本实验装置如图3所示。半导体激光器(HNL210L-氦氖激光器,Thorlabs)发出波长为632.8 nm的连续波光束,首先通过用于调节光束功率的半波片和偏振分束器,再经过焦距为100 mm(AC254-100-A,Thorlabs)和300 mm(AC254-300-A,Thorlabs)的2个凸透镜(lens1和lens2)所组成的4f扩束系统并经过其中的针孔(Pinhole,P100D,Thorlabs)进行空间滤波,随后具有水平偏振方向、分布均匀的高斯光束照射在第一台空间光调制器(SLM1,LCOS-SLM-X10468-07,Hamamatsu)上。光束经过加载POVB相位图的SLM1以及200 mm的衍射传播后,成为完美涡旋光束,其复振幅作为DNN的输入层信息。在此处放置加载了衍射层相位图的第二个空间光调制器(SLM2,LCOS-SLM-X10468-07,Hamamatsu),作为网络的隐藏层。经过200 mm距离的衍射传播后,输出层的目标场强度最终被电荷耦合器件(CCD)相机(Lumenera,Lt29059C)收集,并利用功率计(1919-R,Newport)记录SLM2前后的功率,计算得出衍射效率。

图3 实验装置示意图。(a)轴棱镜的相位;(b)螺旋相位;(c)透镜相位;(d)产生POVB的相位图Fig.3 Schematic diagram of the experimental setup.The phase patterns of(a)an axicon,(b)a helical phase,(c)a lens function and(d)the POVB

2 实验结果与讨论

实验中,首先选取了ℓ=±1～±4范围内间隔为Δℓ=1的8个OAM状态进行识别。网络输入层的POVB振幅信息结果如图4(a)所示,不同OAM状态POVB经过网络隐藏层的相位调制衍射之后可以被映射至输出平面上的8个不同检测区域[图4(b)中的白色方框],在DNN的设计过程中,规定了白色方框区域表示每个拓扑荷经过训练的目标检测区域,每个区域对应一个拓扑荷。图4(b)展示了入射OAM阶数ℓ=-1的POVB经过DNN后的输出图像,相应的目标区域光强最大。图4(c)、(d)分别展示了网络输出平面上不同OAM状态POVB输入时仿真和实验上各个区域强度分布。结果表明,DNN能将不同OAM状态的POVB的输入能量集中到正确的位置目标探测区域。实验中的光路准直问题导致了实验和仿真的能量分布误差,实验结果表明DNN能够实现对小间隔TC的POVB的分类识别。通过测量隐藏层SLM2入射光束的功率Pin以及出射光束的功率Pout,可以得到每一次分类的衍射效率η=Pout/Pin,结果表明衍射效率可达58%。

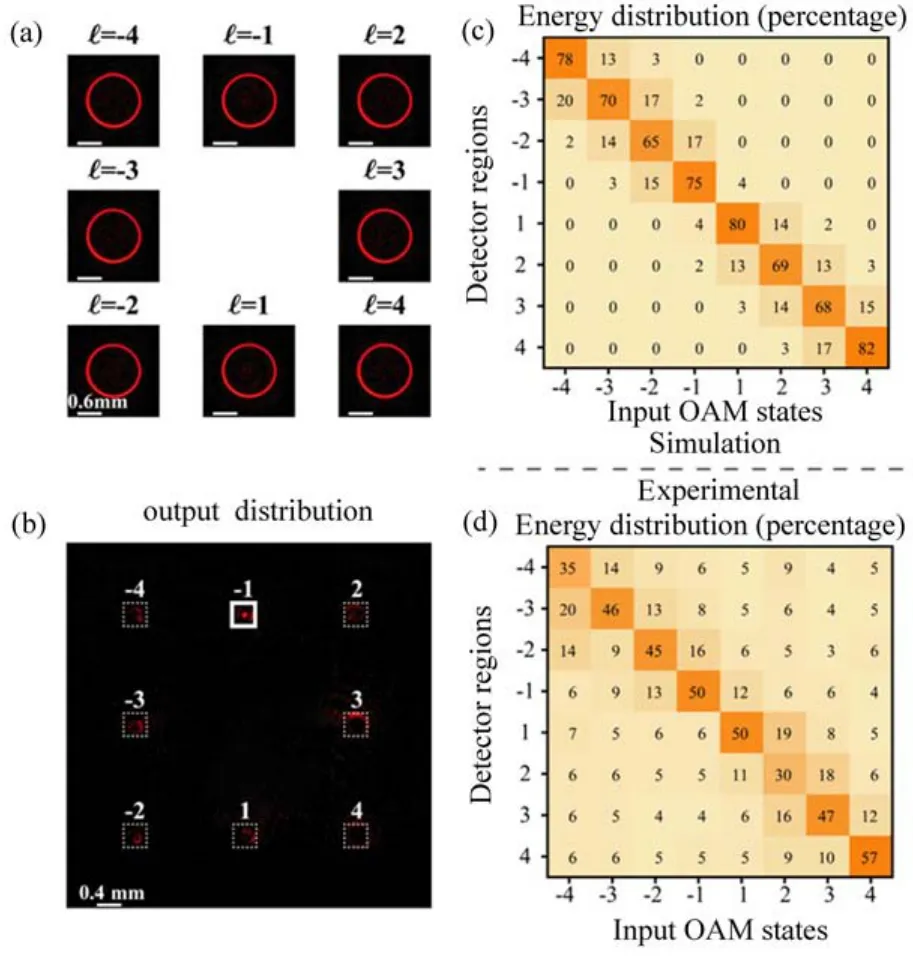
图4 密集OAM状态的POVB分类。(a)OAM阶数为-4～+4的POVB的光强分布;(b)输入OAM阶数ℓ=-1的POVB时DNN输出图像;(c)仿真、(d)实验结果输出平面的各区域能量分布百分比Fig.4 Recognition of POVB with dense OAM orders.(a)The intensity distribution of POVB with OAM order ranging from-4 ～ +4;(b)The output image of the DNN for the incident POVB with ℓ=-1;(c)The simulation and(d)the experimental percentage of energy distribution at distinctive regions of the output plane

为了证明对于高阶OAM状态的POVB仍能利用DNN实现分类,进一步选取了ℓ=-50～+50范围内Δℓ=5的高阶OAM状态POVB[如图5(a)所示]进行分类实验。由于实验中各个光学元件的对准问题,导致了高阶POVB光强分布不均匀。图5(b)展示了轨道角动量状态ℓ=+35的POVB入射时的输出光强图,即使出现高阶POVB光强分布不均匀对称的情况,DNN依然能够准确识别出POVB的OAM状态,这表明DNN对实验中的对准问题具有容错性。图5(c)、(d)对输出平面各区域光强进行了精确的数值分析。结果表明DNN同样能够将高阶OAM状态的POVB输入能量集中到正确的位置目标探测区域,实现分类识别,实验中衍射效率也在58%左右。

图5 高阶OAM状态POVB分类。(a)高阶TC的POVB的光强分布;(b)输入OAM阶数ℓ=+35的POVB时DNN输出图像;(c)仿真、(d)实验得到输出平面各区域能量分布百分比Fig.5 Recognition of POVB with high OAM orders.(a)The intensity distribution of POVB with high-order OAM;(b)The output image of the DNN for the incident POVB with ℓ=+35;(c)The simulation and(d)the experimental percentage of energy distribution at distinctive regions of the output plane

值得指出,构建光学衍射神经网络的方法同样适合区分分数阶OAM与整数阶OAM叠加态的入射光束。当用OAM阶数ℓ=-1和ℓ=+3的叠加态[相位和光强如图6(a)、(b)所示]入射到图4所设计的网络时,可以观察到如图6(c)所示的输出结果,能够发现在图中白色实线矩形框区域得到点状图案,从而判断入射叠加态的OAM成分。当选用分数阶ℓ=-2.5～+2.5范围内Δℓ=0.5的OAM状态的POVB来构建分类探测DNN时,入射OAM分数阶ℓ=-2.5[相位和光强如图7(a)、(b)所示]的POVB,网络的输出结果如图7(c)所示。

图6 叠加态(ℓ=-1和ℓ=+3)OAM状态POVB分类。(a)OAM阶数ℓ=-1和ℓ=+3叠加态的相位;(b)OAM阶数ℓ=-1和ℓ=+3叠加态的光强;(c)输入叠加态POVB时DNN的输出图像Fig.6 Recognition of POVB with the OAM orders of superposition states(ℓ=-1 and ℓ=+3).(a)The phase of superposition state of OAM order ℓ=-1 and ℓ=+3;(b)The light intensity of superposition state of OAM order ℓ=-1 and ℓ=+3;(c)The output image of the DNN for the incident POVB with the superposition states

图7 分数阶OAM状态POVB分类。(a)OAM阶数ℓ=-2.5的相位;(b)OAM阶数ℓ=-2.5的光强;(c)输入OAM阶数ℓ=-2.5的POVB时DNN的输出图像Fig.7 Recognition of POVB with the fractional OAM orders.(a)The phase of OAM order ℓ=-2.5;(b)The light intensity of OAM order ℓ=-2.5;(c)The output image of the DNN for the incident POVB with ℓ=-2.5

值得注意的是,将光路准直以及大气湍流等问题考虑到DNN的设计当中,同样可以完成密集OAM状态的POVB探测识别。当OAM状态ℓ=+3的POVB入射到特殊设计的DNN当中,能够得到如图8所示的输出结果。同时还对比了在相同情形下,叉形光栅对OAM探测的结果。因为传统的基于叉形光栅的OAM检测方法,是利用相反的螺旋相位进行相干叠加,在+1衍射级处得到清晰的高斯亮点,从而判断入射光束的OAM模式,而如今光束受到光路准直以及大气湍流的影响,相当于叠加了一个随机相位因子,造成模式串扰与波前紊乱,无法通过模式转换变为高斯模式,所以能够发现叉形光栅无法完成对POVB的OAM状态探测识别。但是将光路准直以及大气湍流考虑在内所训练的DNN仍然能够完成这项任务,拥有更好的鲁棒性。

图8 特殊环境下DNN与叉形光栅探测POVB的OAM状态。(a)光路准直问题;(b)大气湍流环境Fig.8 Detection of OAM state of POVB by DNN and fork grating in special environment.(a)Optical path collimation problem;(b)Atmospheric turbulent environment

3 结论

提出了一种基于全光衍射神经网络实现不同OAM状态的POVB识别的实验方案,通过角谱衍射传播理论计算神经网络输出并运用梯度下降算法优化参数,证明了密集间隔(Δℓ=1)、高阶OAM态的POVB(ℓ=-50～+50)均可以通过DNN实现识别,同时还研究了网络的输出平面的能量分布和衍射效率。在光通信等应用中,因为DNN具有容错性,在构建DNN时可以将大气湍流等因素考虑到训练参数当中,以对抗外界因素所带来的影响,所以在特殊的环境下,同样可以实现高准确率的推测。此外,实验中受限于SLM像素尺寸带来的影响,无法实现更多拓扑荷的分类,未来还可以基于高度集成化、高分辨率的光学超表面器件构建光学衍射神经网络[30],同时,这也为人工智能光学芯片的设计、应用开创了新的道路。