用旋转多普勒方法解析矢量涡旋光的偏振特征

贾俊亮,张笑儒,赵子丹,张沛∗

(1西安交通大学国家级物理实验教学示范中心,陕西 西安 710049;2西安交通大学物质非平衡合成与调控教育部重点实验室,陕西 西安 710049;3西安交通大学陕西省量子信息与光电量子器件重点实验室,陕西 西安 710049)

0 引言

矢量空间分布偏振光场(简称矢量光场)是电磁场亥姆霍兹方程的矢量解[1]。普通涡旋光场的偏振是空间均匀分布的,而矢量涡旋光的偏振则是非均匀分布,即其在矢量光同一横截面的不同位置处偏振态不相同。本文涉及一种被广泛研究的矢量光场即柱形矢量光(CVB),其偏振分布具有柱对称性,是不同于均匀偏振的涡旋光场。这种光场又称为矢量涡旋光,是自旋与轨道角动量(OAM)[2]二者性质的结合。CVB的对称性所带来的更丰富的性质使其在诸多领域有着广泛的应用价值,例如超分辨率成像[3-5]和光学捕获[6-8]。除了其对称性,矢量光的不同模式之间具有的正交性也有很大的利用空间,其中一个重要的例子是模分复用(MDM)[9,10],这种技术使用多个正交的光场模式作为信息载体完成高容量的通信过程。矢量涡旋光作为MDM的载体相比于标量涡旋光[11,12]具有更大的信息容量。因其在各领域的应用价值,CVB的生成和检测已经成为一个很有意义的研究话题。研究人员已经提出了许多生成CVB的方法,其中一个最简单的方法是利用q-plate,它是一种具有特定分布的液晶装置[13]。另外,特殊设计的激光谐振腔可以直接输出具有偏振分布的激光[14]。最近,本课题组研究人员提出了一种使用偏振选择性Gouy相移器的新的无源生成技术,这种方法能够同时生成任意多模式的CVB[15],方便对矢量光装置进行集成化设计,为柱矢量光尤其是矢量涡旋光提供了进一步的研究基础和研究空间。CVB的检测则可视为生成技术的逆向技术,上述生成技术均有潜力改造为检测技术,比如q-plate可以结合分束器和单模光纤,将低阶CVB分别解复用到不同的单模光纤中,通过检测光纤出口信号可直接辨别模式特征[16]。

在研究含轨道角动量的光场时,旋转多普勒效应是一种有效的工具。当具有螺旋相位的光束照射到以角速度Ω旋转的物体时,反射光将经历频率和轨道角动量的变化[17,18],其中频移与入射光与反射光的轨道角动量量子数差成正比,这种现象称为光场的旋转多普勒效应。旋转多普勒效应与更普遍的线性多普勒效应实际上有着相同的起源,两者可以被视为彼此的特例[19]。它们均源于光源与观测者的相对运动,分别适用于直线运动和同轴旋转运动的研究。旋转多普勒效应不仅适用于单色光源,也适用于含有轨道角动量的白光入射光[20],因此可应用于遥感测量等非单色光源的应用场景。

本文聚焦的是运用旋转多普勒效应的CVB检测技术。其它检测方法可以简单得出各低阶CVB模式的组成,而借助旋转多普勒效应可以进一步得出CVB的详细偏振特征。CVB的偏振特征在偏振片的辅助下,可以内禀性地测出偏振手性和物体转动的手性是否一致,进而可以在无参考光的情景下分辨遥远物体的旋转方向[21],在与均匀偏振的OAM探测的比较中极具优势。矢量涡旋光按照左右旋偏振态的叠加相位的不同,偏振分布表现为任意点的偏振态与该点方位角呈线性变化。本工作用旋转角的概念来定义CVB的特性,提出并分析偏振旋转角的变化率和初相位两个参数,进而甄别两种手性相反的CVB。

本文首先描述了柱矢量光偏振态旋向与其左右旋偏振态相对相位的关系,随后讨论了矢量光场旋转多普勒效应产生的拍频效应,并展示了光强随时间变化的函数及其初相与矢量光的偏振旋转方向的关系,最后借助实验来论证理论的正确性。

1 理论分析

如果一束光具有螺旋相位特性,则可携带光学OAM,用符号标记为

式中:ℓ表示OAM的拓扑荷,即涡旋光拓扑荷;(r,φ,z)为空间柱坐标;e-iℓφ代表螺旋相位;C|ℓ|(r,z)则包含拉盖尔-高斯项、古伊相位等旋转多普勒效应无关量[22,23]。

结合高阶庞加莱球(HOPS)的概念[10,24],可以将一对拓扑荷相反的OAM光束与不同的圆偏振耦合组成矢量光场,定义为

式中:狄拉克符号|L〉和|R〉表示左旋和右旋偏振态,(2υ,2γ)为HOPS球面上任意点的极角与赤道角。以(2)式为标准,OAM的拓扑荷也可以用来表示矢量涡旋光的角向拓扑荷,ℓ的符号即矢量涡旋光的正负号,本研究的目标即检测ℓ的符号。

ℓ的符号在矢量涡旋光中的物理意义是矢量涡旋的旋转方向。(2)式可以根据关系|L〉=分解到水平偏振|H〉和竖直偏振|V〉并用琼斯矢量来表示,令υ=π/4,矢量涡旋光的偏振态为

可计算出偏振方向沿着角向的空间变化角度(相对于水平方向,逆时针方向为正方向,暂称为旋向角)为

式中:ℓ恰好为角度的变化率,ℓ的符号对应变化率的正负,γ则表示在φ=0位置的初始角度。

矢量涡旋光的旋向角由初始角度和变化率共同决定,图1展示了|ℓ|=1的典型情况。结合(4)式可知,偏振矢量与方向的夹角为常数γ,因此,矢量光的偏振参量γ此时可以作为衡量矢量光场偏振态旋转程度的标准。对于γ=0的矢量光,其偏振方向与径向一致,此时偏振不存在旋转。当γ>0时,各点偏振态将会向方位角φ的正向偏转,γ<0时则向负方向偏转。更为一般的情况下,ℓ为任意整数,γ则可表示(0,π)区间内任意相位。图1(a)～(f)分别展示了ℓ=±1、γ=0,±π/4的矢量涡旋光的偏振分布。图1(a)～(c)的变化率为正,即ℓ=1,其中(a)的偏振态呈无旋向的径向分布,即γ=0;(b)的偏振分布在(a)的基础上向正方向旋转,呈右手螺旋,γ=π/4;(c)为左手螺旋,γ=-π/4。图1(d)～(f)的变化率为负,即ℓ=-1,偏振分布不再具有明显的手性特征,但依然可以按照(4)式中的参数描述,其中(d)的偏振态情形γ=0,(e)和(f)的偏振情形分别为γ=π/4和γ=-π/4。

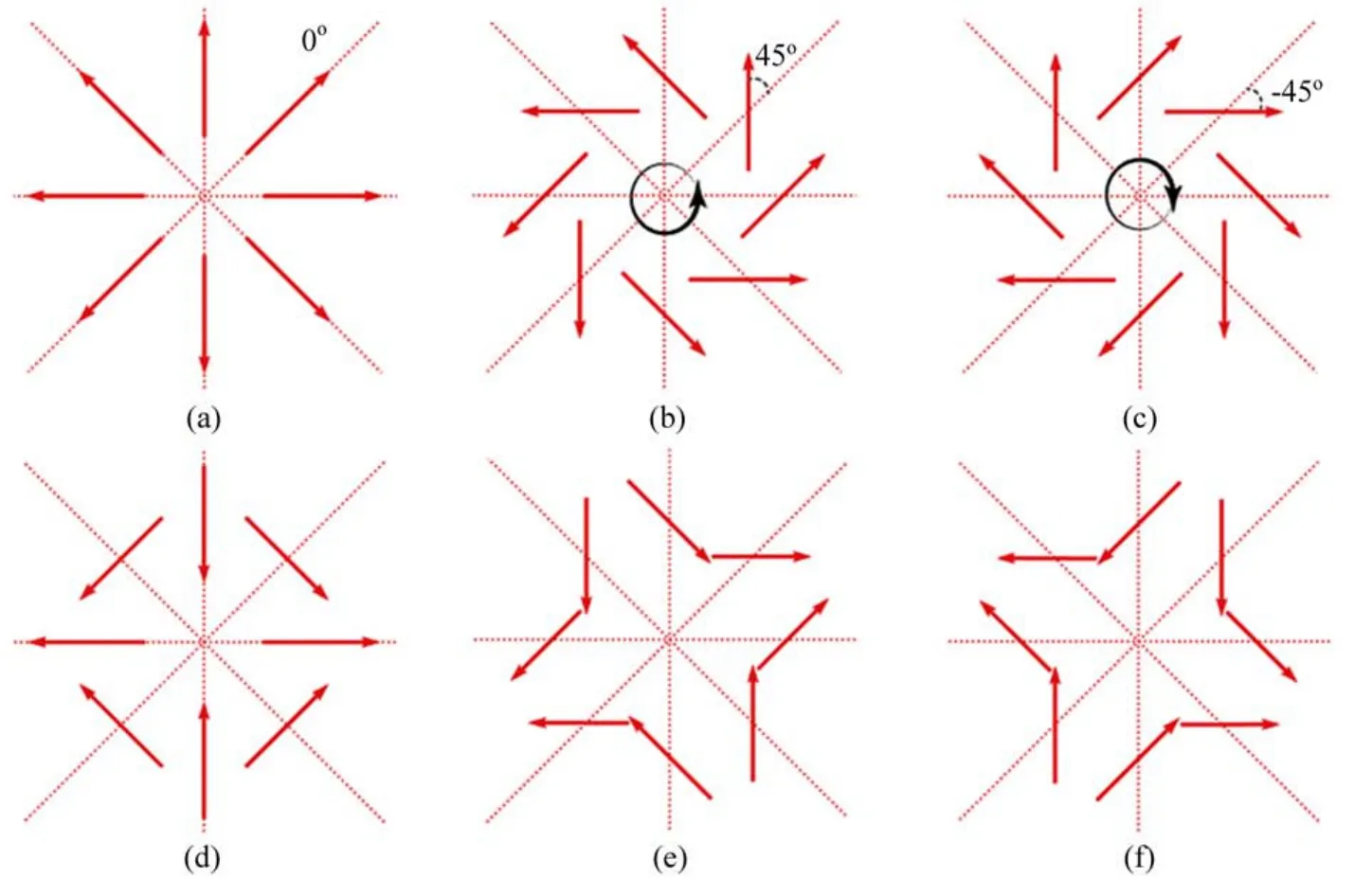
图1 矢量涡旋光的偏振分布。(a)ℓ=1,γ=0;(b)ℓ=1,γ=π/4;(c)ℓ=1,γ=-π/4;(d)ℓ=-1,γ=0;(e)ℓ=-1,γ= π/4;(f)ℓ=-1,γ=-π/4Fig.1 Polarization distribution of cylindrical vector beams.(a)ℓ=1,γ=0;(b)ℓ=1,γ= π/4;(c)ℓ=1,γ=-π/4;(d)ℓ=-1,γ=0;(e)ℓ=-1,γ= π/4;(f)ℓ=-1,γ=-π/4

理论上,旋转物体等价于多个同速度旋转的螺旋相位板的叠加,其不同模式之间的叠加系数与旋转物体表面的各阶螺旋成分的权重有关。光束经过旋转物体之后,旋转多普勒效应产生的频率移动与涡旋光经过旋转物体前后拓扑荷的变化量相关,频率变化量符合

式中:Ω为物体的旋转角速度,n=Δℓ表示光束经过旋转物体前后OAM拓扑荷的变化值。旋转物体的调制函数可以利用傅里叶级数表示为[19]

式中|An(r,φ)|为叠加振幅,n取整数,表示光束经过旋转物体前后的拓扑荷改变量。叠加系数选取时结合拍频信号原理及OAM的正交性,可增强有效信号的强度。

例如,对于矢量涡旋光拓扑荷为ℓ的实际情形,可以选取n=±ℓ,且|Aℓ|=|A-ℓ|,则可有效增强基模拍频信号的强度。在经过旋转物体散射后,出射的光场将具有不同的OAM模式。同时,从(2)式中可以看出,对于某一柱形矢量光,其内含有拓扑荷数相反且振幅相等的两种螺旋相位。因此在选取适当的旋转物体的情况下,散射光的同一OAM模式(如基模)中将含有两种不同频率的信号来源,探测二者的总光强可产生拍频效应,得到二者的差频信息。将(2)、(6)式相乘并检验水平偏振方向的光强,归一化后可得拍频信号符合变化规律

由于不同OAM模式之间的正交性,对于单一矢量涡旋光的情形,散射后的光强中不存在不同模式之间的交叉项。所以,经过(6)式描述的物体后分析特定模式(如ℓ=0)的光强信号,通过傅里叶变换可以得出旋转多普勒频移2ℓΩ以及相位δ。

δ的数值由三部分共同决定,其一为入射矢量涡旋光的参数γ,其二可以在(6)式中为每一项引入额外相位(本文为0),其三为实验设计中偏振器件(如波片组)自由引入的定量几何相位,如图2(a)所示的2个半波片(HWP)和1个四分之一波片(QWP)组合。(7)式表明,当入射CVB的拓扑荷ℓ为正的时候,δ>0则光强函数发生相位提前,δ<0则发生相位延迟;当拓扑荷为负的时候则相反。因此,根据拍频曲线随δ的变化规律可得出矢量涡旋光拓扑荷的符号。进一步,结合具体情况校正以上三种相位,可以根据(4)式得出入射CVB完全的旋向特征。

2 实验结果与讨论

实验示意图如图2所示。先用任意可行方法(如q-plate,干涉仪等)产生CVB。本研究采用图2(a)所示实验光路,用He-Ne激光器作为偏振光源,用半波片(HWP1)和四分之一波片(QWP1,QWP2)的组合制备任意偏振态,以满足实验中的相位移动。之后光束经过q-plate产生ℓ=1的CVB,在q-plate之后额外加入角度为0的半波片则可产生ℓ=-1的CVB。CVB经过分束器(BS)的引导,先后经过空间光调制器(SLM)上加载的全息光栅[26][如图2(c)所示]的调制及透镜加小孔(Iris)的滤波,最终光强随时间变化的数据被CCD成功采集。全息图加载的内容按照(6)式在条件|A1|=|A-1|≠0设定,可以保证全息图的图案旋转时在SLM的一级衍射中采集到光的拍频信号。图2(b)展示了本实验中发生旋转多普勒效应的物理模型(其中黄色和蓝色部分分别代表左旋和右旋成分的波前等相位面)。在以上设定下,旋转物体将ℓ=±1的CVB展开成平坦波前,并且同时CVB的两种偏振成分发生干涉,产生拍频。实验采用的SLM具有水平偏振响应,因此通过投影计算可知实际产生了(7)式描述的信号。

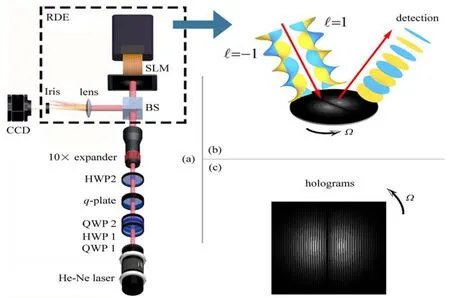
图2 实验方案示意图。(a)实验光路图;(b)旋转多普勒效应示意图,黄色和蓝色波前等相位面分别对应矢量涡旋光的左旋和右旋成分;(c)SLM加载光栅的图片展示Fig.2 Experimental implementation.(a)Schematic of experiment;(b)Schematic of measurement with rotational Doppler effect where red and blue components represent left and right-handed wave front respectively;(c)Hologram shown on SLM

实验中,半波片(HWP1)和四分之一波片(QWP1,QWP2)的组合用以引入额外几何相位δ(图中示意为γ,即δ的其它两部分视为0,方便理论关系的对应)。图3展示了不同矢量涡旋光拍频的理论数据。在图3(a)中,入射涡旋光拓扑荷ℓ=1,实验中半波片额外引入的几何相位为δ=0,π/4,可以发现δ=π/4对应的曲线相对于δ=0的曲线发生了向左的平移,即发生了相位提前;在图3(b)中,入射涡旋光拓扑荷ℓ=-1,实验中半波片额外引入的几何相位为δ=0,π/4,可以发现δ=π/4对应的曲线相对于δ=0的曲线发生了向右的平移,即发生了相位延迟,因此根据曲线的移动方向可以直接得出涡旋光拓扑荷的正负号信息;在图3(c)中,入射涡旋光拓扑荷ℓ=1,实验中半波片额外引入的几何相位为δ=0,-π/4,可以发现δ=-π/4对应的曲线相对于δ=0的曲线发生了向右的平移,即发生了相位延迟。比较图3(a)和图3(c)可知,在拓扑荷符号相同的情况下,拍频方法也可以方便测出矢量涡旋光参数γ的正负;比较图3(b)、(c)可知,额外几何相位对于曲线的移动具有补偿效果(负负得正),这种补偿技术在复杂成分分析中往往可以用来补偿各成分之间的相位差。图3(d)、(e)、(f)分别为图3(a)、(b)、(c)对应的实验数据,图3(a)、(b)、(c)采用的实验拟合公式I=0.79+0.21cos(2Ωt±π/4)符合(7)式的理论预测。拟合结果多出的直流部分可由实验中的光源质量、器件误差、光栅衍射效率共同决定。另外,从图3(d)、(e)、(f)的实验结果可以看到,在实验数据中有个别测量点偏离了曲线,这是因为使用的q-plate在某些位置存在缺陷,使得物体旋转到特定角度时光强会发生骤降。

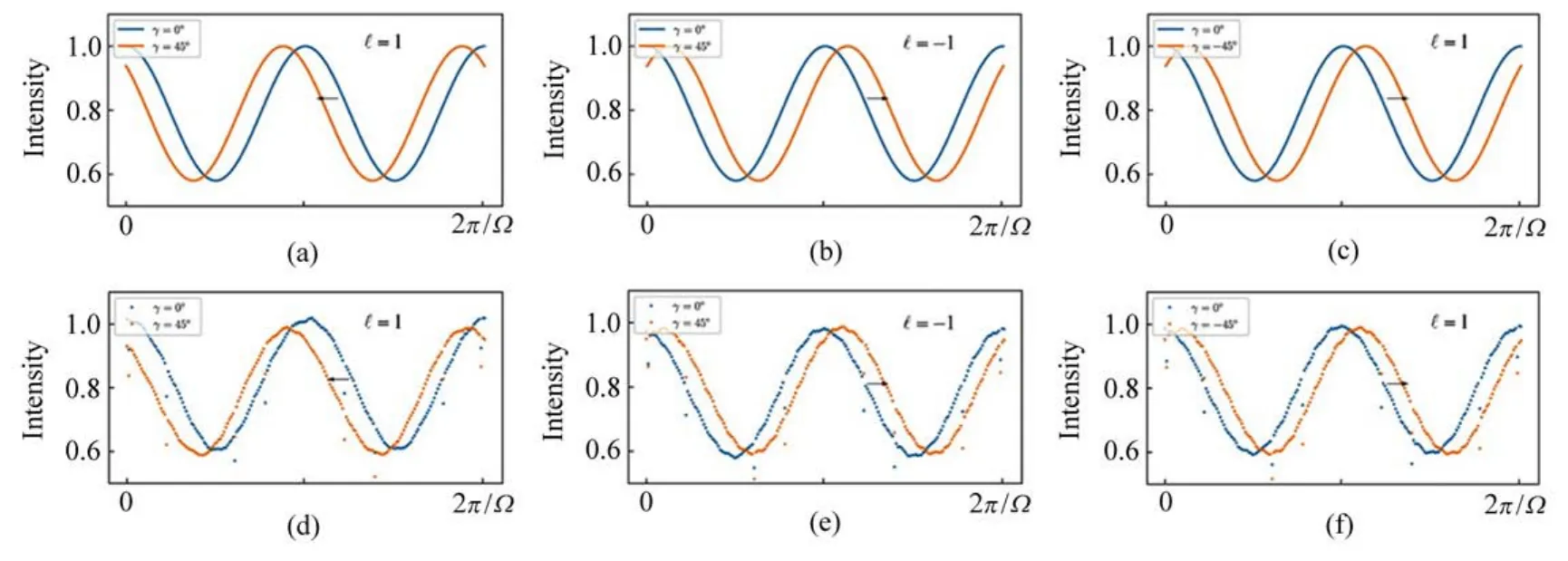
图3 归一化拍频信号[(a)～(c)理论模拟;(d)～(f)实验数据]。(a)ℓ=1,δ=0,π/4,偏振正向旋转,相位超前;(b)ℓ=-1,δ=0,π/4,偏振正向旋转,相位超前;(c)ℓ=1,δ=0,-π/4,偏振负向旋转,相位延迟;(d),(e),(f)分别为(a),(b),(c)对应的实验数据Fig.3 Normalized beating signal[(a)～(c)Theoretical simulation;(d)～(f)Experimental results].(a)Phase advance of positively rotated polarization state in ℓ=1, δ=0,π/4;(b)Phase delay of negatively rotated polarization states in ℓ=-1, δ=0,π/4;(c)Phase delay of positively rotated polarization state in ℓ=1,δ=0,-π/4 with opposite phase operation;(d),(e),(f)are experimental results corresponding to(a),(b),(c)

3 结论

提出了一种利用旋转多普勒效应区分矢量涡旋光偏振旋转特征的方法。当矢量光的偏振态相对某一确定的偏振态发生整体旋转时,其相位将发生移动。拓扑荷相反的两种CVB在同一偏振操作下发生的移动方向不同,因此可以通过拍频曲线的移动方向来区分CVB拓扑荷的正负,进而还原出CVB的偏振特征。实验上测量了两种相反拓扑荷的矢量涡旋光,并用径向矢量光作为参考,利用半波片控制并在拍频系统中测量了矢量涡旋光的相位移动。实验结果与理论预期符合,证实了该方法的正确性。在后续研究中可以利用该方法完成对矢量光偏振参数的测量。