涡旋光场相干调控及拓扑荷测量

王卓异,曾军,张浩,卢兴园,赵承良∗,蔡阳健,∗

(1苏州大学物理科学与技术学院,江苏 苏州 215006;2山东师范大学物理与电子科学学院,山东 济南 250358;3山东省光场调控工程技术中心,山东省光学与光子器件技术重点实验室,山东 济南 250358)

0 引言

自然界中的涡旋现象随处可见,如船舶和桨尾流中的水涡流,以及热带气旋、龙卷风等等。在光学领域中也存在类似的涡旋结构,即光学涡旋。光学涡旋是指在光场中的涡旋结构,其特点是等相位线沿着方位角成螺旋状分布,所有等相位线汇聚为一点,形成相位奇点,在该点处振幅为0,而相位具有不确定性。Nye和Berry在1974年提出“光的波列位错”,奠定了以光学涡旋为主要研究对象的“奇点光学”的核心理论[1],进而使得光学涡旋成为研究热点。1989年,Coullet等[2]在流体力学涡旋的启发下,找到了Maxwell-Bloch方程的涡旋解,发现了类似流体涡旋的模式,并提出了光学涡旋的概念。涡旋光束是光学涡旋的典型代表,通常可由涡旋相位exp(ilθ)表征,其中l和θ分别代表拓扑荷和方位角。拓扑荷l通常为整数,可定义为在一个波长内相位扭转次数,l的正负取决于相位的旋转方向,l越大表示光沿着光轴旋转的越快。1992年,Allen等[3]提出了涡旋光束可以携带相当于每光子lħ(l是整数)的轨道角动量,揭示了宏观光学与量子效应之间的联系。这些研究开创了现代光学的新篇章,即奇点光学,这是传统光学发展的一大飞跃。光学涡旋基于其具有轨道角动量的特点,在光学微操纵、大容量光通信、超分辨成像等领域具有广泛应用[4-9]。

初期对光学涡旋的研究主要在完全相干光领域,但是在一些特定的应用场景中,高空间相干性反而会引起不利因素,如容易引起光场散斑严重、光斑闪烁等,而通过降低激光束的空间相干性,反而能克服以上问题,如部分相干光在经过大气湍流传输时要比完全相干光具有更强的抗湍流大气扰动,以及更小的光斑漂移,因此更适合用于大气光通信。1998年,Gori等[10]首先将涡旋结构引入部分相干光场并提出了部分相干涡旋光束。基于Wolf等的光场偏振与相干理论[11],近二十年人们根据完全相干光中的各种涡旋光束模型[3,12,13],相继提出了具有高斯谢尔模关联[14]、拉盖尔关联[15]、多高斯关联[16]、厄米关联[17]结构的新型部分相干涡旋光束。相比于完全相干涡旋光束,部分相干涡旋光束有其独特的传输特性,如自聚焦、自分裂和自重构效应[17,18]。与完全相干涡旋光束的光强不同,部分相干涡旋光束的光强分布会随着相干度的变化而变化,通过调控相干度以及拓扑荷可以产生空心分布、平顶分布和高斯分布等多种光斑结构。

矢量部分相干涡旋光束,是一种携带涡旋相位矢量的部分相干光,同时具有涡旋相位、部分相干光和矢量光束的特有属性,多维度对光场实现调控,可以实现相干诱导的光束整形和涡旋相位诱导的光斑旋转。而聚焦的部分相干径向偏振涡旋光束,其涡旋相位可以影响传输过程的偏振度。通常随着拓扑荷l值的增加,偏振度增加,这意味着涡旋相位在传播中起到反退偏振的作用。

部分相干涡旋光束的应用离不开该涡旋光源的产生,常见产生部分相干涡旋光束的方法是通过在部分相干非涡旋光束中加载涡旋相位。其中,部分相干光源可通过提升非相干光束的相干性[19,20]、或者降低完全相干光束的相干性[21-24]以及完全相干光束的非相干叠加[25-27]三种方式实现,而涡旋相位可通过涡旋相位板[14]、计算全息[22]、螺旋线[28]光学结构等来加载。另外,也可通过涡旋光束作为相干模式进行非相干叠加直接实现部分相干涡旋光束的产生[29,30]。

涡旋光束的很多应用都基于其拓扑荷/轨道角动量特性,因此能够精准、快速地检测拓扑荷具有重要的实际意义。早期提出的拓扑荷测量方案几乎都是基于完全相干涡旋光束的拓扑荷测量,例如夏克哈特曼测量法[31]、衍射法[32]、干涉法[20,33-35]、傅里叶变换法[36]、螺旋谱分析法[37]等,虽然它们能够有效测出拓扑荷大小或符号,但是当涡旋光场的空间相干性降低时,以上方法将失效。为此,针对部分相干涡旋光场,研究者陆续提出了关联函数法(双相关函数[23]、复相干度[38]、微扰法[39]、双缝干涉法[24,40,41])等方案以实现低相干性条件下涡旋光束拓扑荷的检测。

早期研究涡旋光场时往往侧重整数拓扑荷的涡旋光场。1995年,Basisty等[42]首次观测到涡旋光束光强“甜甜圈”上具有径向开口的现象,也就是分数阶涡旋光束。后来,研究者对分数阶涡旋光束进行了大量研究,包括分数平面波涡旋光束、分数高斯型涡旋光束和分数贝塞尔光束[43-47]。分数阶涡旋光束在量子纠缠[48,49]、微粒操纵[4,50,51]、相位成像[52-54]等领域有着重大的应用前景。近期Zeng等[55,56]将分数阶涡旋光束拓展到部分相干光场中,分别构建了标量和矢量部分相干分数阶涡旋光束,操纵部分相干分数阶涡旋光束的空间相干性和拓扑荷为其研究光束传输特性和光束整形铺平了道路,对微观粒子的引导和传输以及信息传递提供了先进的理论基础。

本文第1节详细介绍了部分相干涡旋光束的理论,其中包括常用物理基本概念及部分相干高斯谢尔模涡旋光束、部分相干拉盖尔-高斯光束、各种特殊关联的涡旋光束以及部分相干矢量涡旋光束的理论模型,同时还给出了不同涡旋光束的光强分布与相干度分布;第2节介绍了常见产生部分相干涡旋光束的方法,重点介绍了利用毛玻璃降低相干度的方法,和通过计算全息图以及螺旋相位板产生涡旋相位的方法;第3节讨论了拓扑荷的测量方法,重点介绍了柱透镜模式转换法、微扰法以及双缝干涉法;第4节介绍了部分相干涡旋光束的应用,包括自由空间光通信、信息传输与加密、光操纵。第5节介绍了分数阶涡旋光束的性质,最后是总结与展望。

1 部分相干涡旋光场理论

1.1 部分相干涡旋光束理论

1802年,Young[57]在双缝干涉实验中观测到明暗相间的条纹图案,也就是后来广为人知的杨氏干涉实验,由此开启了光学相干性研究的大门。条纹的明暗对比度与光源有关,而这个“对比度”的定义一直到1938年才被Zernike完整定义[58]。Zernike提出一种数学表达式,定义了相干度这一概念,可以用其描述双缝干涉时的对比度。它可以通过互强度的概念进行表示,互强度的定义为

式中:t表示时间,E(r,t)表示电场。在随机电场理论中,互强度表示E(r1)和E(r2)之间的关联程度。两点之间光场的复相干度为

式中I(ri)表示ri点的平均光强,可以表示为

之后Wolf[11]提出了更加广义的定义来描述随机电场,即互相干强度与交叉谱密度,它们可以用来表示部分相干光束的统计特性。

标量部分相干光束的统计特性可以用时空域的互相干函数或空间频域的交叉谱密度来表征,交叉谱密度与互相干函数互为傅里叶变换关系。与此同时Wolf[11]还发现互相干函数与交叉谱密度函数在自由空间分别满足波动方程和广义亥姆霍兹方程,这表明相干度可以像光波一样传输。源平面上部分相干涡旋光束的交叉谱密度可以表示为

式中:E(r)和T(r)分别为电场和振幅。角括号〈〉和星号∗表示系综平均和共轭运算,r1与r2表示源平面上的位置矢量坐标,φ=arctan(y/x)是角坐标,l表示拓扑荷,µ(r1-r2)为两点间的关联函数。通过调控振幅T(r),可以产生不同光强分布的部分相干涡旋光束;通过调控关联函数µ,可以产生不同关联结构的部分相干涡旋光束。

部分相干涡旋光束在自由空间中的传输可以利用惠更斯-菲涅耳积分研究,而利用下面的广义柯林斯公式则可以研究部分相干涡旋光束通过近轴ABCD光学系统的传输[59,60]。经过ABCD光学系统的近轴传播后,部分相干涡旋光束的交叉谱密度可以写成

式中:A、B是光学系统中传递矩阵的元素;k=2π/λ,λ是波长;W(r1,r2)和W(ρ1,ρ2)分别表示源平面以及接收面的交叉谱密度函数。接收平面内部分相干涡旋光束的光场强度和相干度分别为[61]

完全相干条件下的涡旋光束在传输远场处具有特定的涡旋相位分布和中央暗核结构,而对于谢尔模型关联的部分相干涡旋光束,随着相干度的降低以及拓扑荷的减少,在传输过程中中央暗核会逐渐缩小直至消失,中心光强则会逐渐增强[10,21,22,62,63]。当受到湍流影响或者相干度较低时,大多部分相干涡旋光束光强会退化到高斯分布[40,64,65]。众所周知,完全相干涡旋光束在光源平面和传输过程中都携带有相位奇点[66,67]。这里相位奇点的定义为:光场的强度为零且相位不确定的点。也就是说在传输过程中,部分相干涡旋光束不再携带相位奇点,而此时部分相干涡旋光束会逐渐产生关联结构的奇点,称为相干奇点或关联奇点。关联奇点定义为[68]

式中:Re和Im分别表示取实部和取虚部运算,(ρ1,ρ2)表示关联奇点的坐标。Swartzlander等[69]通过理论和实验验证了部分相干涡旋光束在传输过程中相干奇点的存在(即环形位错)。激光束的相干度分布也就是它的关联结构分布。随着相干度的逐渐降低,这一环形位错逐渐变得清晰,而此时对应的相位奇点逐渐消失。一般来说,相干奇点的数量取决于部分相干涡旋光束的拓扑荷。

1.2 传统关联结构—谢尔模型涡旋光束

1.2.1 高斯谢尔模涡旋光束

对于部分相干涡旋光束来说,如果在源平面满足(4)式,且T(r)分布为高斯分布,关联结构µ(r1-r2)也为高斯分布并且带有涡旋相位,则称这种光束为高斯谢尔模(Gaussian Shell model)涡旋光束[14],在源平面交叉谱密度函数可表示为

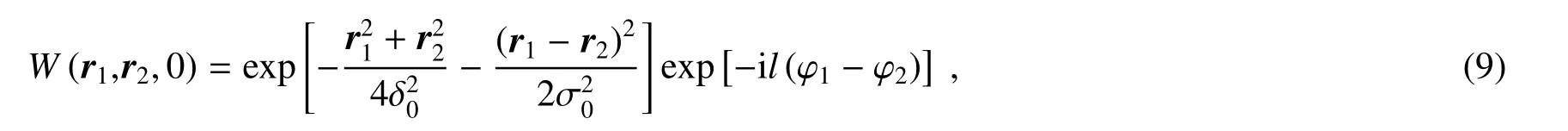
式中:δ0表示源平面高斯谢尔模涡旋光束的束腰宽度,σ0表示初始相干长度。当σ0=∞时退化成完全相干光束,当σ0=0时退化成完全非相干光束。

完全相干涡旋光束在源面上或在自由空间中传输时呈现出暗空心光束轮廓。对于部分相干涡旋光束,其高相干光束在焦场也表现为暗空心光束轮廓,但由于源空间相干性的退化,其焦场光束轮廓在传输过程中会发生变化,可以通过改变初始相干宽度来整形部分相干涡旋光束在焦平面上的光斑[14]。例如,当相干宽度逐渐减小时,焦场光斑的轮廓会从暗空心光束轮廓逐渐转变为平顶光束轮廓,最后转变为高斯光束轮廓,如图1(b)所示。此外,当初始相干度一定时,部分相干涡旋光束的光斑也可以通过改变其初始拓扑荷来进行光束整形,因为拓扑荷起到了抗相干性引起的空心退化作用,如图1(a)所示。

图1 具有不同拓扑荷与初始相干度的高斯谢尔模涡旋光束焦场光强分布Fig.1 Intensity distribution of Gaussian Shall mode vortex beam at focal plane for different topological charge and initial coherence width

1.2.2 部分相干拉盖尔高斯光束

部分相干拉盖尔高斯(Laguerre-Gaussian,LG)光束在源面上的交叉谱密度可表示为[63]

图2 不同σg、l的部分相干标准聚焦光强图[22]Fig.2 Focused intensity of partially coherent standard beam for different values of σgand l[22]

图3 不同p、l的部分相干标准拉盖尔高斯光束和部分相干完美拉盖尔高斯光束(b)聚焦光强图Fig.3 Focused intensity of partially coherent standard Laguerre-Gaussian beam(a)and partially coherent elegant Laguerre-Gaussian beam(b)for different values of l and p

由图2、图4可以看出相干长度以及拓扑荷数都会对光斑尺寸产生影响。当光束经过透镜聚焦后,部分相干涡旋光束的拓扑荷、相干长度等参数在焦平面处都可对远场光强进行整形,相干度减小时部分相干标准与完美拉盖尔高斯光束光强分布都会从空心逐渐模糊,最终形成高斯分布。增大拓扑荷数会减缓空心光束演化为高斯光束。

图4 不同相干长度的部分相干标准(a)与完美(b)拉盖尔高斯光束的焦场强度(l=2,p=2)。Fig.4 Focused intensity of partially coherent standard(a)and elegant(b)Laguerre-Gaussian beams with different coherence length(l=2,p=2)

Siegman[70]提出了一种厄米高斯(Hermite-Gaussian)模式,这种模式也满足傍轴近似的波动方程,被称为完美的厄米高斯模式。后来根据此理论研究人员提出完美拉盖尔高斯光束可以作为标准拉盖尔高斯光束的延伸[71-73]。由于拉盖尔多项式是一个复宗量而不再是实数,完美拉盖尔高斯在拉盖尔函数与高斯函数的自变量中具有相同的复数因子,因此完美拉盖尔高斯光束具有更对称的形式。由于复宗量参数的引入,使得完美拉盖尔高斯光束的光强与相干度与标准拉盖尔高斯光束完全不同。完美拉盖尔高斯光束作为其他光学谐振器模态扩展和传播的基础,已得到广泛的应用。2009年,Wang等[63]提出了部分相干标准和完美拉盖尔高斯光束,它是相应完全相干光束的自然延伸。发现在相同环境下,部分相干完美拉盖尔高斯光束与相应的标准拉盖尔高斯光束相比有许多优点。例如,相对于部分相干标准拉盖尔高斯光束,部分相干完美拉盖尔高斯光束的传播特性受湍流的影响较小,且其在自由空间和湍流大气的演化过程较慢等。

1.3 特殊关联涡旋光束

通过对光场振幅与相位的调制[13,74,75],可以产生高斯谢尔模涡旋光束、部分相干拉盖尔高斯光束、部分相干贝塞尔光束等。对于光场调控,不仅可以调控光场的振幅、相位,还可以对相干结构进行调控[76-78]。得益于Gori等[79,80]对构建特殊空间关联部分相干光束的理论研究,Mart´ınez-Herrero等[81,82]提出了构建部分相干光束的充分条件。自此,提出了大量特殊空间关联结构的部分相干激光束模型,包括多高斯关联部分相干激光束[77]、拉盖尔-高斯关联部分相干激光束[72]、厄米-高斯关联部分相干激光束[72]、余弦-高斯关联[78]部分相干激光束等等。

1.3.1 多高斯谢尔模型涡旋光束

根据多高斯谢尔模(Multi-Gaussian Schell model)光束的自然延伸,Zhang等[16]提出了一种新的部分相干涡旋光束,它的相干度满足多高斯分布,称为多高斯谢尔模型涡旋(MGSMV)光束,其在源面上的交叉谱密度可表示为

由(11)、(12)式可知,多高斯谢尔模型光束的相干度可以看作是高斯函数的有限叠加,随着M的增加,多高斯谢尔模型光束的相干度逐渐变为非高斯分布[16]。

如图5所示,对于多高斯谢尔模型涡旋光束,聚焦光束轮廓随着M的增加而逐渐平坦。有趣的是,具有较大拓扑荷l的多高斯谢尔模型涡旋光束的光斑演化成平顶光束的速度比具有小拓扑荷l的多高斯谢尔模型涡旋光束的光束轮廓平顶的速度慢。因此,调制多高斯谢尔模型涡旋光束的光束阶数M也可以整形其聚焦光束轮廓。

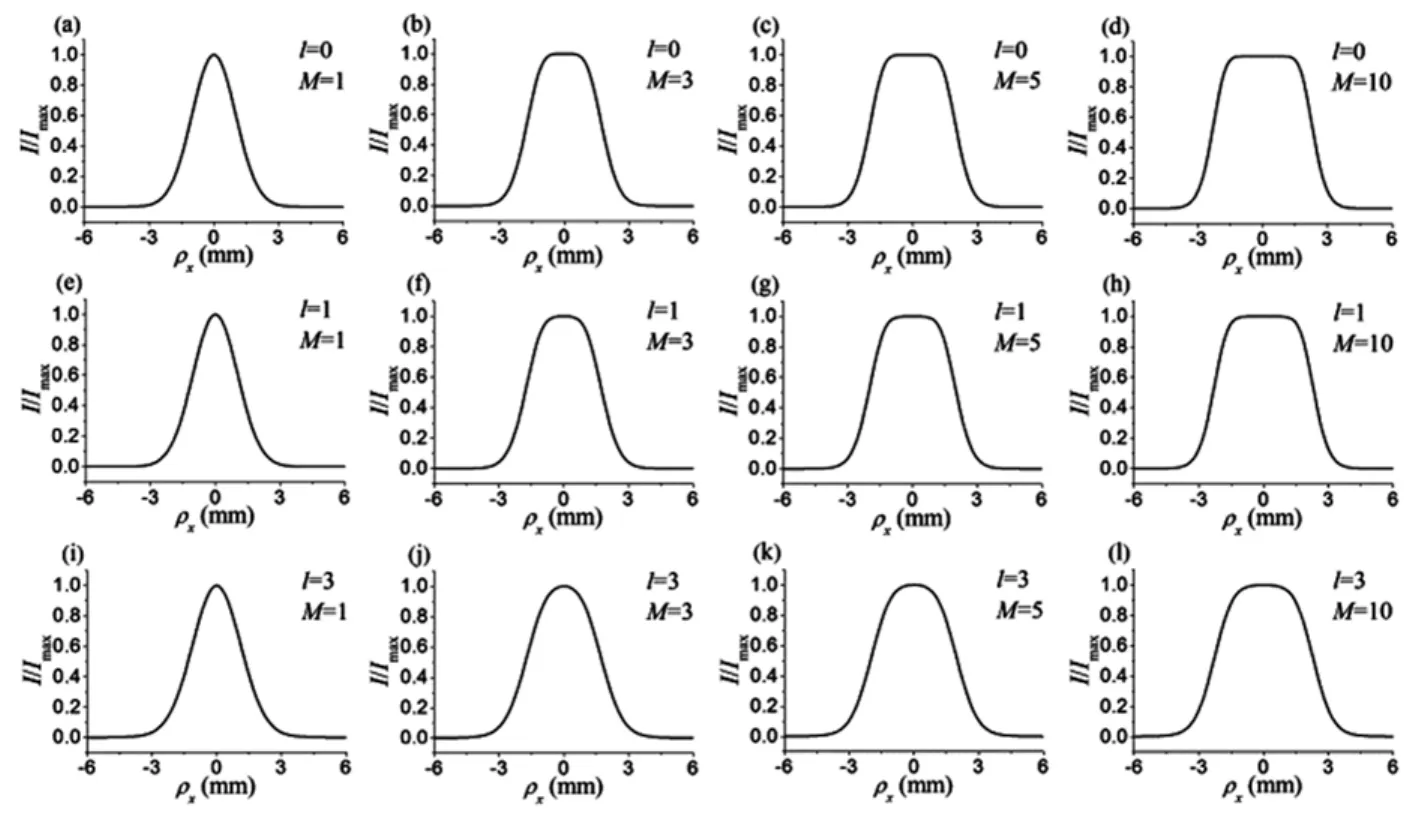
图5 σ=1 mm,δ=1 mm,λ=632.8 nm时,多高斯谢尔模型涡旋光束在不同拓扑电荷l和光束阶数M下的焦平面上的(z=f)[16]归一化强度分布Fig.5 Normalized intensity distribution of a MGSMV beam at the geometrical focal plane(z=f)for different values of the topological charge l and the beam index M with σ =1 mm,δ=1 mm and λ =632.8 nm[16]

1.3.2 拉盖尔高斯关联的涡旋光束

2014年,Chen等[15]又提出一种具有拉盖尔高斯关联的部分相干涡旋(Laguerre-Gaussian correlated Schell model vortex)光束。对于拉盖尔高斯关联的涡旋光束,其源平面处交叉谱密度函数定义为

式中G0是一个常数。z=0时拉盖尔高斯关联的光束的相干度表示为

从图6可以看出拉盖尔高斯关联的涡旋光束表现出有趣的传输特性,其中n是拉盖尔高斯关联函数的阶数,l为拓扑荷数。当初始相干宽度σ0较小时,拉盖尔高斯关联的涡旋光束在远场的光强分布具有暗空心光束轮廓。随着初始相干宽度的增加,拉盖尔高斯关联的涡旋光束的远场强度分布发生变化,远场暗空心光束轮廓也随着初始相干宽度的增加而逐渐消失,而当初始相干宽度较大时,远场暗空心光束轮廓再次出现。上述有趣的现象可以用以下方式解释:空间相关函数对部分相干光束演化特性的影响只有在初始相干度较低时才起主导作用,而在初始相干度较高时其影响可以忽略不计。可以看出对于拉盖尔高斯关联的涡旋光束,其演化特性由拉盖尔高斯关联的关联函数和涡旋相位共同决定。当初始相干度较低时,拉盖尔高斯函数起主导作用,涡旋相位的影响可以忽略不计;当初始相干度较高时,涡旋相位的影响占主导地位,拉盖尔高斯关联函数的影响可以忽略。由于涡旋相位的影响,拉盖尔高斯关联的涡旋光束的远场光强出现暗空心光束轮廓,在光束中心存在相位奇点。

图6 不同初始相干宽度σ0下拉盖尔高斯关联的涡旋光束在自由空间中传播不同距离的归一化强度分布,其中n=1,l=3[15]Fig.6 Normalized intensity distribution of a Laguerre-Gaussian correlated Schell model vortex beam with n=1 and l=3 at several propagation distances in free space for different values of the initial coherence width σ0[15]

随着初始相干度的增加,拉盖尔高斯关联的涡旋光束在焦平面上的暗空光束轮廓逐渐消失。当初始相干度较大时,拉盖尔高斯关联的涡旋光束的光强具有暗空心光束轮廓。对于合适的初始相干宽度,拉盖尔高斯关联的涡旋的强度呈现平顶光束轮廓。因此,调制拉盖尔高斯关联的涡旋光束的空间相干性提供了一种新的整形聚焦光束轮廓的方法,这将有助于粒子捕获。其中聚焦的高斯或平顶光束光斑可以用于捕获折射率大于环境折射率的瑞利粒子,而暗空心光束光斑可用于捕获折射率小于环境折射率的瑞利粒子。

通过调控关联结构还可以产生其他关联结构的部分相干涡旋光束,如厄米高斯关联函数拉盖尔高斯光束[17]。当相干长度较小时,光强主要由关联函数决定;当相干长度较大时,光强主要由涡旋相位决定。由于这种特殊的相干度分布,厄米高斯关联部分相干涡旋光束在自由空间中传输可以表现出自分裂特性[17]。这里只列举了这几种具有特殊空间关联结构的部分相干涡旋光束,其他特殊空间关联结构的部分相干涡旋激光束的模型可以通过构建不同关联结构[83-85]再加上不同的涡旋相位产生。由于空间关联结构的差异,它们在传输过程中将会表现出不同的性质。

1.4 矢量部分相干光束

以上介绍的几种具有特殊空间关联结构的部分相干激光束均为标量光束,矢量部分相干激光束同样具有重要的研究价值。矢量部分相干光场是矢量光场和部分相干光场的结合,其偏振态是空间非均匀分布的,且相干性为部分相干。矢量部分相干光场同时具有矢量光场和部分相干光场的性质和应用,在自由空间传播、光学干涉、光与物质相互作用等方面展现出丰富的偏振和相干特性[86,87]。在空间根据相干和偏振的统一理论,矢量部分相干光束的二阶统计特性[11,80,88]可以用2×2交叉谱密度矩阵W(r1,r2)表征为

对于高斯谢尔模光源产生的部分相干径向偏振光束,在极坐标系,其源平面中的交叉谱密度矩阵的矩阵元W(r1,r2)可以用W(ρ1,θ1;ρ2,θ2)表示,定义为[88]

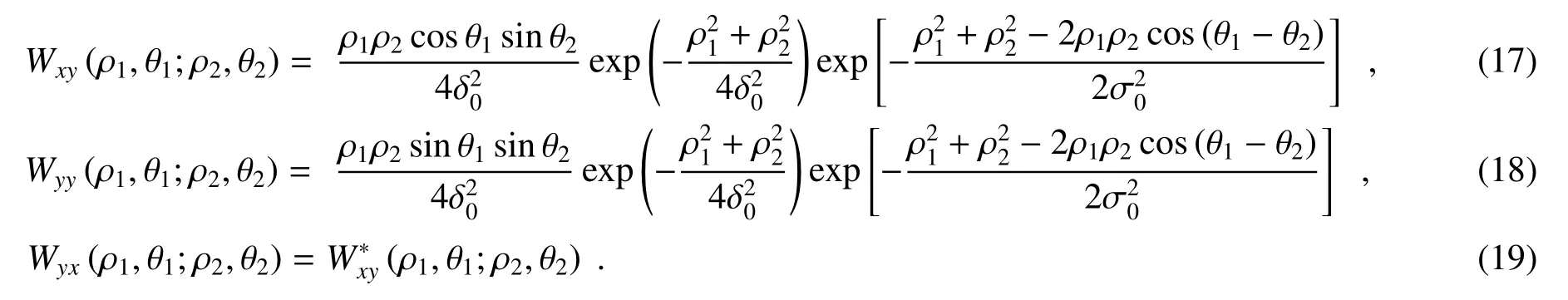
对于带有涡旋相位的部分相干径向偏振光束,其交叉谱密度矩阵的元素可以表示为

如上面所述,涡旋相位将导致部分相干径向偏振光束在传输过程中的统计特性发生显著变化,这可以应用于粒子捕获与旋转。

在图7与图8中,给出了携带不同拓扑荷(l=0,±2)的部分相干径向偏振涡旋光束经透镜聚焦后在不同传输距离处的I及其分量Ix与Iy的光强分布。对于完全相干径向偏振光束,其具有空心光束轮廓的中央暗核结构,并且在自由空间传输中始终保持暗空光束轮廓。而聚焦部分相干径向偏振光束在传输过程中光谱强度分布I的演化特性与聚焦完全相干径向偏振光束有很大的不同。例如,部分相干径向偏振光束初始暗中空光强分布在传输过程中演化成具有平顶分布的光斑,最后在焦面上变成高斯光斑(图7),这是因相干宽度减小引起的。而聚焦部分相干径向偏振光束与聚焦部分相干径向偏振涡旋光束也有很大的不同。聚焦部分相干径向偏振光束(l=0)的Ix和Iy在传播时不旋转(见图7),但聚焦的部分相干径向偏振涡旋光束(l=2)的Ix和Iy在传播时沿逆时针旋转(l=2时沿顺时针旋转),见图8。当Ix和Iy在传播时旋转,这意味着总光强I在传播时也会旋转(由于I的圆对称特性使得旋转特性并没有被体现)。光束光斑的旋转是由涡旋相位所施加的轨道角动量引起的。相干诱导的光束整形和涡旋相位诱导的光斑旋转现象对粒子的捕获和旋转是有用的。完全相干径向偏振涡旋光束(σg=∞)的偏振度等于1,并且在传输过程中保持不变。而部分相干径向偏振涡旋光束由于受到涡旋相位的影响偏振度会在传输过程中发生变化,随着拓扑荷l值的增加,偏振度增加,这意味着涡旋相位在传播过程中起到反退偏振的作用[89]。

图7 当l=0时,不同传输距离下的聚焦径向偏振光束I及其分量Ix与Iy在x-y平面的光强分布,实心曲线表示一维曲线[88]Fig.7 Spectral intensity distribution I and its components Ixand Iyof a focused partially coherent radially polarized vortex beam with l=0 in the x-y plane at several propagation distances.The solid curve denotes the cross line[88]

图8 (a)l=2,(b)l=-2时,不同传输距离下的聚焦径向偏振光束I及其分量Ix与Iy在x-y平面的光强分布,实心曲线表示一维曲线[88]Fig.8 Spectral intensity distribution I and its components Ixand Iyof a focused partially coherent radially polarized vortex beam in the x-y plane at several propagation distances with(a)l=2 and(b)l=-2.The solid curve denotes the cross line[88]

2 部分相干涡旋光束实验产生

一般来说,部分相干涡旋光束的产生主要包括两个步骤:第一步是产生部分相干光束,第二步是将涡旋相位加载到产生的部分相干光束中。

2.1 部分相干光束产生

产生部分相干光束的方法有多种:一种是利用滤光片[20,90](如小孔、狭缝等)来增加非相干光束的相干宽度,这种方法在激光发明之前就得到了广泛的应用。这种方法不仅体积大,而且产生光束的初始相干宽度是不可控的。根据范西特泽尼克定理,非相干光束在远距离传输后可以演化为部分相干光束;第二种方法是借助随机介质(例如旋转毛玻璃[91-94]、动态液晶体[95])来减小完全相干光束的相干宽度。这种方法可以通过控制旋转毛玻璃表面的光束光斑大小来精确控制产生的部分相干光束的初始相干宽度,但会造成激光能量的损失,并且旋转毛玻璃会引起环境的振动;第三种方法是模式叠加[25,96],因为部分相干光可分解为多个完全相干光的非相干叠加,用这种方法产生的部分相干光的功率相对于第二种较高。

目前调控光束的相干度主流方法主要是后两种。下面通过产生部分相干光束(高斯谢尔模光束)来介绍第二种方法。图9(a)显示用来产生高斯谢尔模光束的实验装置,激光经过扩束镜扩束后由薄透镜L1聚焦到旋转的毛玻璃上,当毛玻璃上的光斑远大于其磨砂颗粒的大小,则经过毛玻璃散射后产生的光束为完全非相干光束[97],根据范西特泽尼克定理,当特定光强的非相干光束通过准直薄透镜L2和高斯滤波片后,透射光束就变为强度和相干度均满足高斯分布的高斯谢尔模光束。高斯谢尔模光束的空间相干性由聚焦到旋转的毛玻璃上的光斑大小和毛玻璃的粗糙度共同控制。一般在实验中,毛玻璃的粗糙度是固定的,所以主要通过改变毛玻璃上聚焦光斑的大小来调制空间相干性。打在毛玻璃上的光斑越大对应相干度越小。同时可以通过控制打在毛玻璃上的光强分布构建不同关联函数的部分相干光束。

第三种方法是通过叠加一系列模式来产生部分相干光[26],用这种方法不会降低产生的部分相干光的功率。Wolf在上世纪80年代提出[100-102],在一般的条件下,部分相干涡旋光场表达式也可以用本征模的形式表示为

其中函数φn(r,ω)相互正交。利用这一新的展开式,可以构造频率ω相同、电场为φ(r,ω)的模式叠加,其产生的交叉谱密度作为空间频率域中的相关函数,如图9(b)所示通过空间光调制器产生完全相干光场φn(r,ω),通过时间平均代替空间平均以及对应的权重λn(ω),即可产生部分相干涡旋光束。同样,交叉谱密度函数W(r1,r2)还可以用随机模[103,104]以及伪模[27,79,81]进行构建。

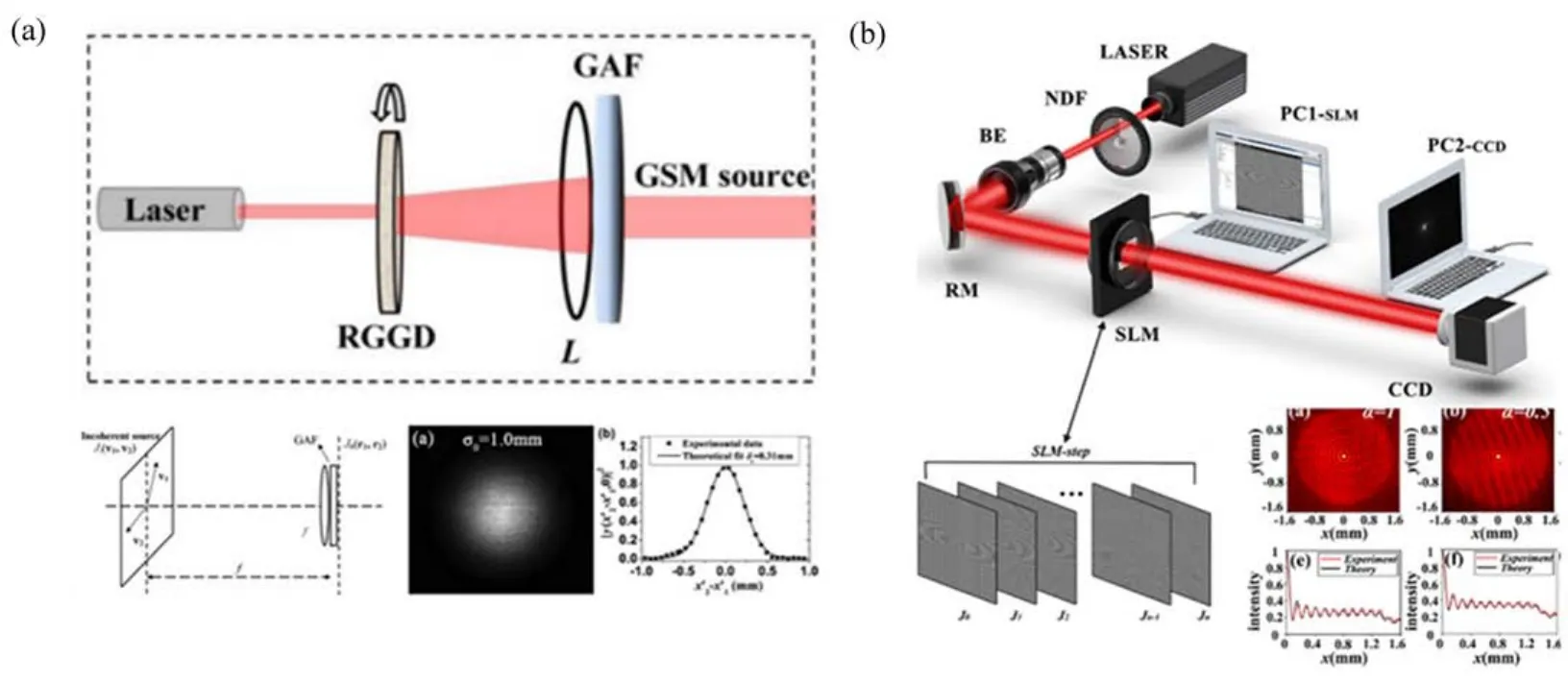
图9 产生部分相干光束的实验装置。(a)通过旋转毛玻璃产生部分相干光束[98];(b)通过模式叠加产生部分相干光束[99]Fig.9 Experimental setup for generating a partially coherent beam.(a)Experimental setup for generating a partially coherent beam via rotating ground-glass disk[98];(b)Experimental setup for generating a partially coherent beam via mode superposition[99]

通过采用模式叠加的方法可以产生任意关联函数的部分相干光束,并且产生的部分相干光的功率较高、可调节性大。动态散射体产生法的优势在于能够实时产生,且产生的光束模型依据SLM的灵活调控能实现多样化,但是对相干性的调控需要手动移动部分光学元件(透镜)来实现。

2.2 涡旋相位产生

涡旋相位可以通过螺旋相位板产生[17,20,22,105,106],螺旋相位板可以看成一个相位物体。其透过率函数定义为exp[ilφ],其中φ是方位角。通过螺旋相位板不但可以产生整数阶涡旋光束,还可以产生分数阶涡旋光束。通过螺旋相位板产生涡旋光束转换效率较高,而且能对高功率激光光束进行转换。它的缺点是一个螺旋相位板理论上只能产生单一拓扑荷数的涡旋光束,且对加工技术要求比较高。理想情况下,相位的变化是平滑连续的,但由于制作工艺的限制,实际应用中使用阶梯型的螺旋相位板。螺旋相位板在处理一些需要高功率的激光束或是小型化的仪器时,是其他任何方法都无法替代的。

同样利用叉形光栅也可以产生涡旋光束[23,39,41,107-109],叉形光栅是依据光的干涉和衍射原理设计的。可以通过计算全息法得到叉形光栅,利用计算机编程实现目标光与参考光的干涉图样,参考光通过干涉图样即可得到涡旋光束。图10(a)显示用来产生部分相干光束的实验装置[21,22],激光经过扩束镜扩束后由薄透镜L1聚焦到旋转的毛玻璃上,再通过准直薄透镜L2和高斯滤波片后,透射光束就变为强度和相干度均满足高斯分布的高斯谢尔模光束。随后产生的高斯谢尔模光束进入空间光调制器,通过空间光调制器加载涡旋相位以及振幅调制后所产生的光束即为部分相干拉盖尔高斯光束。其中拉盖尔高斯光束的拓扑荷l可以通过空间光调制器进行调制。利用计算全息法产生涡旋光束是一种快速灵活、应用范围广泛的方法。相比于其他方法,叉形光栅产生法可以根据应用需求比较灵活便捷地控制光束的各个参数,产生出质量较高的涡旋光束。缺点是空间光调制器对通过的光束有能量的限制,不能处理功率高的激光束,同时由于光栅通过空间光调制器加载,因此光栅质量受空间光调制器限制。

部分相干涡旋光束也可以用模式叠加的方法直接产生,如图10(b)所示实验激光束通过相位型空间光调制器产生单个模式作为随机模进行线性非相干叠加,每种模态平均贡献一个与相应模态特征值的权重。当产生足够多的模式数,模式与权重符合(21)式,可以认为实验产生的部分相干光与理论吻合。

图10 产生部分相干拉盖尔高斯光束的实验装置。(a)通过旋转毛玻璃产生部分相干涡旋光束[22];(b)通过模式叠加产生部分相干光束[26]Fig.10 Experimental setup for generating a partially coherent Laguerre-Gaussian beam.(a)Experimental setup for generating a partially coherent vortex beam via rotating ground-glass disk[22];(b)Experimental setup for generating a partially coherent beam via mode superposition[26]

产生涡旋光束的方法还有很多种。例如:模式转换法,即通过柱面镜[3]将不带涡旋相位的厄米高斯光束转化为带有涡旋相位的拉盖尔高斯光束,以及光通过具有特定结构的狭缝[28,110,111]也可以产生涡旋相位。

3 涡旋光束拓扑电荷的测量

3.1 完全相干涡旋光束拓扑荷的测量

涡旋光场的光子携带轨道角动量,它与拓扑荷密切相关,可用于信息编码和解码。一般来说,要对拓扑荷信息进行编码,需要知道拓扑荷的大小和符号。测量涡旋光束的拓扑荷数对了解涡旋光束的基础知识及其应用具有重要意义。夏克-哈特曼波前传感器具有测量范围宽、光学效率高等优点,是目前应用最广泛的波前传感器,其工作原理是通过微透镜阵列将入射光场划分为多个子光场,通过微透镜阵列聚焦并记录在相机中。通过分析光斑图案与参考测量的偏差可以导出局部方向角,进而能够重建波前,因此可以用夏克-哈特曼波前传感器直接探测光束的拓扑荷数[31]。另外涡旋的强度分布包含了涡旋的拓扑荷信息,在光强的傅里叶变换中,暗环的数目等于涡旋的拓扑荷数。对于拓扑荷数较小的涡旋光束,可以清晰地看到暗环数。然而对于高阶涡旋,由于环数较多便无法得出暗环数目,但是可以利用基于拉盖尔多项式的正交性得出高阶涡旋拓扑荷数[36]。对于完全相干涡旋光束拓扑荷测量,还有许多方法如衍射法[32]、干涉法[20,33-35]、螺旋谱分析法[37]等。

3.2 部分相干涡旋光束拓扑荷的测量

对于高相干的部分相干涡旋光束的拓扑荷,可以用与完全相干光束类似的方法进行测量。但是当光源相干性降低,光强分布将受到相干性的影响,适用于完全相干涡旋光束的拓扑荷测量方法也将失效。

与完全相干光束不同的是,部分相干光束具有一定的统计特性,即部分相干光束有一定的关联结构。下面主要对部分相干标准拉盖尔高斯与部分相干完美拉盖尔高斯光束的复相干分布进行描述,部分相干高斯涡旋光束的关联结构与部分相干模光束的关联结构相似,这里不再赘述。

如图11(a)所示,部分相干标准拉盖尔高斯光束远场相干分布中的环形位错数目与径向指数p和拓扑荷l有关。仔细观察部分相干标准拉盖尔高斯光束的远场相干分布,可以得到部分相干标准拉盖尔高斯光束的关联结构环形位错数N与径向指数p和拓扑荷数l之间的关系为N=2p+|l|。图11(b)显示了p和l对部分相干完美拉盖尔高斯光束远场相干分布的影响。由图11(b)可以看出,p并不影响远场相干度分布中的环位错数目,也就是说,环位错的数目只取决于拓扑荷数|l|,这与部分相干标准拉盖尔高斯光束的情况有很大的不同[38,106]。

图11 不同l与p的部分相干标准与完美拉盖尔高斯光束远场相干度分布(σ0=0.3δ0)。(a)部分相干标准拉盖尔高斯光束的远场相干度分布;(b)部分相干完美拉盖尔高斯光束的远场相干度分布Fig.11 Far- field degree of coherence of partially coherent standard and elegant Laguerre-Gaussian beams with different l and p(σ0=0.3δ0);(a)Far- field degree of coherence of partially coherent standard Laguerre-Gaussian beam;(b)Far- field degree of coherence of partially coherent elegant Laguerre-Gaussian beam

通过图11可以得出复相干度暗环数与拓扑荷数有关,2012年,Zhao等[22]提出了部分相干涡旋光束远场复相干度与拓扑荷满足

式中:k表示波数;ω表示频率;ρ,θ表示远场极坐标;B是光学系统中传递矩阵的元素。此后,研究者提出通过测量部分相干涡旋光束远场的关联函数来测量拓扑荷,主要有基于HBT法和自相干微扰法的测量复相干度方案。

图12 (a)测量部分相干拉盖尔-高斯光束的实验装置;(b)在不同l和ε条件下,部分相干拉盖尔高斯光束通过两个柱面透镜后传输z=300 mm处的光强与复相干度模的演化图。第一行为光强,第二行为复相干度模[112]Fig.12 (a)Experimental setup for measuring a partially coherent Laguerre-Gaussian beam;(b)Evolution of intensity and complex degree modulus of coherence of the generated partially coherent Laguerre-Gaussian beam after passing through a couple of cylindrical lenses at z=300 mm for different l and ε.The first line is intensity,and the second line is mutual correlation function[112]

根据部分相干涡旋光束理论,离轴的相干度分布包含暗核与暗环,并且暗核和暗环的数目分别与拓扑荷数l和径向指数p的大小完全一致。同样交叉谱密度里也包含拓扑荷与径向指数的信息,通过比较交叉谱密度的相位分布,可以看出相干度模分布中的暗荷数对应交叉谱密度相位分布中相位奇点数。相干度模分布中暗环数对应交叉谱密度的环形位错数。因此,可以从相位分布中同时获得径向指数p的大小(环形位错数)和拓扑荷大小(相位跃变数)及符号(相位变化的方向)。Lu等与Zeng等[39,109]提出利用自参考全息技术来实现交叉谱密度的测量,进而测量拓扑荷大小与正负。在待测面引入了一个参考点r0(可移动的相位微扰点),如图13(a)、(b),利用空间光调制器可以将微扰点自由地移动到目标平面上强度非零的任何点(即照明区域内)。若r0足够大,照明部分相干光源的关联函数足以覆盖待测物体信息范围,且相位均匀分布,光强的反傅里叶变换就能直接得到待测光场的信息;若r0太小,导致物体及其共轭像发生重叠,可以赋值微扰两次,这样和无微扰的情况共同构成一个方程组,便可以求解得到最终所需的光场信息,如图13(c)。从图13(c)第一行可以知道部分相干光束中暗核数等于拓扑荷大小,暗环数等于径向指数p;第二行可以看出中心相位不确定点的数量(即相干奇点数)就是拓扑荷数,其中相位沿顺时针方向增长则表示拓扑荷为负数,沿逆时针增长则拓扑荷为正数,另外,相位中的环形位错数对应于径向指数。

图13 (a)测量部分相干光束复相干交叉谱密度函数的原理图;(b)是(a)的目标平面细节图;(c)参考点在离轴时不同径向指数部分相干拉盖尔高斯光束在焦平面上的交叉谱密度函数的模和相位分布。紫色点表示位于r0处的扰动点[109]Fig.13 (a)Schematic for measuring the complex-valued cross-spectral density function of an arbitrary partially coherent beam;(b)The target plane detail of(a);(c)Experimental results of the modulus and phase distributions of the cross-spectral density function with an off-axis reference point of a partially coherent Laguerre-Gaussian beam in the focal plane with different mode indices.The purple spot denotes the perturbation point located at r0[109]

对于高相干光束来说,可以通过测量衍射或干涉后的光强分布来确定相干涡旋光束的拓扑荷。例如光束通过双缝干涉时[41],对于非涡旋光束(l=0),干涉条纹沿狭缝的长轴均匀分布,如图14(I)所示。然而当涡旋光束通过双缝时,由于两缝之间的相位差从0到2lπ,所以会导致干涉条纹出现扭曲。干涉图样与涡旋光束的拓扑荷直接相关,当拓扑荷数为正数时干涉条纹从干涉的顶部向底部往左移动[图14(I)],当拓扑荷数为负数时干涉条纹从干涉的顶部向底部往右移动。拓扑荷越大,经过双缝干涉后移位条纹偏离越大。因此,可通过观察干涉条纹的移位长度及方向来获得拓扑荷数大小与符号。

当部分相干涡旋光束的光强分布随着初始相干宽度的减小而从“甜甜圈”逐渐演化为高斯分布,由于强度分布严重变形,干涉条纹也会逐渐模糊。通过双缝干涉观测条纹的方法也会失效,2020年,Chen等[24]用部分相干涡旋光束进行了杨氏双缝实验,研究发现部分相干涡旋光束通过双缝后焦面的交叉谱密度携带有拓扑荷信息。交叉谱密度分布相对于轴上参考点的相位可以同时定量地表征这种光束所携带的拓扑荷的符号和大小。拓扑荷的大小是相干奇点数目的一半[如图14(b)],并且拓扑荷的符号由相干奇点的相位(即逆时针方向和顺时针方向的增加方向分别对应于拓扑荷的正和负)。

图14 (a)理论与实验拉盖尔高斯光束经过双缝后的远场干涉图样[113];(b)不同相干度、拓扑电荷的部分相干涡旋光束通过双缝时交叉谱密度函数的相位分布实验结果[24]Fig.14 (a)Far- field interference patterns of theoretical and experimental Laguerre-Gaussian beams passing through double slits[113];(b)Experimental results of the phase distribution of the cross-spectral density function for a partially coherent vortex beams passing through a double-slit with different topological charges and spatial coherence[24]

采用柱透镜将高斯涡旋或者光束转化为厄米高斯光束,可以确定拓扑荷大小与方向,它不仅适用于整数阶拓扑荷的测量,还适用于定性测量分数阶拓扑荷。但是它对于光束是无法准确测量的,对于拓扑荷较大的部分相干高斯涡旋光束也只能定性地测量拓扑荷大小,无法进行定量的测量。同样双缝干涉法也无法适用于光束的测量,只适用于高斯涡旋以及涡旋光束的测量。通过光强的傅里叶变换以及光强焦场的复相干度可以测量部分相干高斯涡旋光束以及部分相干光束。对于部分相干标准拉盖尔高斯光束,复相干度中的暗环数等于2p+|l|,仅仅通过测量远场的复相干度模是不够的,因此Liu等[23]与Yang等[114]提出双关联结构,用来测量指数p,进而可以确定拓扑荷数。而微扰法测量待测平面的交叉谱密度信息不仅适用部分相干标准模,也适用其他关联的部分相干涡旋光束[17,39,109]。近几年随着分数阶部分相干涡旋光束的提出,更多的测量方法也被提出,如通过测量轨道角动量谱测量涡旋光束的拓扑荷[115-118]、光强自关联测量[119]、通过机器学习测量[120]等。

4 部分相干涡旋光场的应用

4.1 自由光通信

在自由光通信中,由于受到空间介质的影响,传输过程中会出现信息的丢失,因此抗空间复杂环境的光束在光通信中有很大的应用前景。可以通过湍流来表征空间的复杂环境,图15给出了高斯谢尔模(GSM)光束、标量部分相干涡旋(PCV)光束、无涡旋的部分相干径向偏振(PCRP)光束和部分相干径向偏振涡旋(PCRPV)光束的闪烁指数与初始相干宽度关系的实验与模拟结果[121]。可以看出,闪烁指数随着相干宽度的减小而减小,即相干宽度较小的部分相干光束受湍流的影响较小。当相干宽度较大(σ0>0.12 mm)时,涡旋相位或偏振态对闪烁指数有很大影响。对于相同的相干宽度,部分相干径向偏振光束的闪烁指数值在三种光束中最低[图15(a)],这种优势随着相干宽度的减小而减弱。当相干宽度小于0.12 mm时,三种光束的闪烁指数几乎没有差别。在相干宽度较大的情况下,与部分相干径向偏振光束相比,部分相干径向偏振涡旋光束可以进一步降低湍流诱导的光束闪烁,这意味着部分相干径向偏振涡旋光束在降低湍流诱导闪烁方面比部分相干径向偏振光束更有优势。这种优势随着拓扑荷的增加而进一步增强。

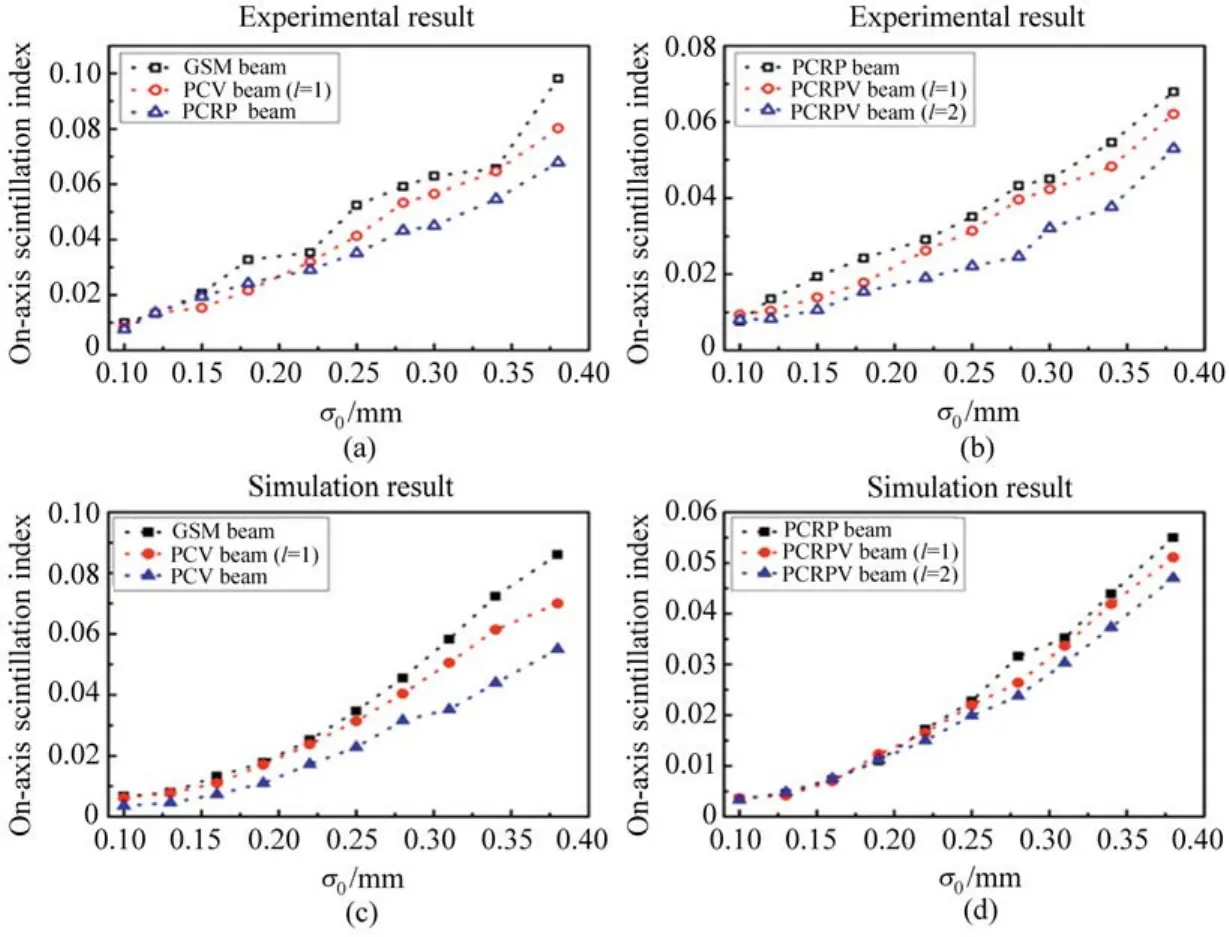
图15 高斯谢尔模光束、部分相干涡旋光束、部分相干径向偏振光束闪烁指数随横向相干宽度变化的实验(a)和仿真(c)结果;部分相干径向偏振和光束l=1和l=2的部分相干径向偏振涡旋光束闪烁指数随相干宽度变化的实验(b)和仿真(d)结果[121]Fig.15 Experimental(a)and simulation(c)results of the variation of the on-axis scintillation of the GSM beams,PCV beams and PCRP beams with the transverse coherence width.Experimental(b)and simulation(d)results of the on-axis SI of the PCRP beams and PCRPV beams with l=1 and l=2 against the coherence width[121]

部分相干标准拉盖尔高斯光束和部分相干完美拉盖尔高斯光束在湍流大气中的特性与其光束参数和湍流结构常数密切相关。一般来说,相干长度越小、光束级数越大、波长越长,部分相干标准和完美拉盖尔高斯光束受湍流的影响越小,但相干长度越小、光束级数越大、波长越长的光束在自由空间中的发散角会变大。与部分相干标准拉盖尔高斯光束相比,部分相干完美拉盖尔高斯光束在克服湍流效应方面具有明显优势,这种优势在较小的结构常数、较大的光束阶数、较大的拓扑荷数、较大的初始相干长度和较长的波长时表现得更为明显[63]。

多高斯关联部分相干光束能够有效地降低湍流引起的光强闪烁,并且湍流越强,多高斯关联部分相干激光束相对于完全相干光束表现出的优势越明显[16]。非均匀关联部分相干激光束相对于传统高斯关联结构的部分相干激光束和完全相干高斯光束,不仅具有更低的闪烁,而且在湍流中传输具有更高的光强[122]。通过调控部分相干激光束的空间关联结构,产生的具有特殊空间关联部分相干激光束能够有效地降低大气湍流带来的负面作用,并且涡旋光束受大气湍流的影响比非涡流光束小,矢量光束相对标量光束在降低湍流诱导闪烁方面有一定的优势。综上具有复杂关联结构的矢量涡旋光束在大气激光光通信领域具有重要的应用前景。

4.2 信息传输与加密

部分相干涡旋光束的另一个有趣而有用的特性是其自修复能力。自修复被认为是相干无衍射光束的特性,如贝塞尔光束、贝塞尔高斯光束和艾里光束[96,123-125]。通常,无衍射光束在与障碍物相互作用时会重建其空间形状。在信息传输与加密中,具有自修复能力的光束将会提供更低的误码率。2021年,Peng等[126]将信息加载到光场的关联结构,通过分数阶傅里叶变换系统进行加密与解密,实验证明了利用关联结构传递信息具有较高的鲁棒性。

以部分相干拉盖尔高斯光束为例,如图16所示,可以发现当聚焦部分相干拉盖尔高斯光束在源面上呈现暗空心光束轮廓,而空心光束轮廓在传输过程中逐渐消失,最终成为焦面上的亮束斑(即高斯光束光斑),但焦平面内的光强分布没有揭示任何有关拓扑荷的信息。在源平面上的相干度呈高斯光束分布,而在焦平面上则表现为环形位错,位错环(即暗环)的数目如预期的那样等于2p+|l|。当α≠0时,虽然源平面内的光强分布被部分遮挡,但在传输时逐渐自修复,最终再次成为高斯分布。同时相干度分布随着传输距离的增加也逐渐出现自重构现象,环形位错的数目逐渐恢复为2p+|l|。部分相干涡旋光束在焦面上的光强分布和相干度分布都可以进行自重构,并且自重构能力随着空间相干宽度的减小而增强[127]。

图16 p=1和l=1的部分相干拉盖尔高斯光束被一个中心角为α的扇形遮挡物遮挡,传输不同距离处的光强归一化分布图(a)与相干度模分布图(b)[127]Fig.16 The density plot of the normalized intensity distribution(a)and the modulus of the degree of coherence distribution(b)of a focused partially coherent Laguerre-Gaussian beam with p=1 and l=1 obstructed by a sector shaped opaque obstacle with center angle α at several propagation distances[127]

部分相干涡旋光束具有轨道角动量,而轨道角动量具有无穷多个模态,且各模态间相互正交,为涡旋波的通信及探测提供了天然的条件。由于具有抗湍流性、多模态性,部分相干光束在光通信、光加密中有广泛的应用前景。

4.3 光学操控

光学操纵主要利用聚焦激光束的辐射力进行捕获与移动粒子。粒子在光束附近时,会受到光对它产生的力的作用,这个力的一个分量指向光强的方向,被称为梯度力;而另一个分量沿着光传播的方向,称为散射力。因此,适当改变光束的聚焦情况可以使这两个力的大小发生改变,从而实现对颗粒的加速、捕获和分离等。自从激光发明以来,光学捕获已经成为一种强大的工具,并成功地应用于各科学领域,如物理、化学和生物物理研究。然而传统的高斯光束只能捕获折射率大于周围环境的透明微粒,并且长时间的高功率聚焦光束将会对微粒产生热效应,极大限制了光镊的应用。Wang等[128]与Cheng等[129]研究了部分相干光束的相干长度对辐射力的影响,提出了可以通过改变相干长度来调控辐射力,2013年,Au˜n´on等[130]提出利用部分相干光进行光操纵,证明即使光强较低也可以捕获粒子,因此利用部分相干光操纵粒子具有极大的优势,逐渐引起人们的关注。

通过调控部分相干光的相干度、拓扑荷、光束阶数等参数可以形成空心、平顶、高斯的光强分布。丰富的光束整形能力将会带来广泛的粒子操纵技术,通过调控部分相干光束的相干度、拓扑荷、光束阶数等参数,可以对辐射力的大小与捕获范围进行调节。对于部分相干平顶光束[6,131],通过增加平顶光束的平坦度(即光束阶数)可以增加焦面附近平面的横向陷阱范围,降低平顶光束的初始相干性可以增加焦面的横向和纵向光阱范围。此外,平顶光束的光阱刚度随着光束阶数的增加或初始相干度的降低而降低。平顶光束的散射力、横向和纵向梯度力随着初始平顶光束相干性的降低而减小。在焦面上,随着平顶光束初始相干性的降低,横向和纵向俘获范围都变大,而光阱刚度则由于辐射力的减小而减小。带有涡旋相位的部分相干光束具有暗空心光强分布特性和携带有轨道角动量特性,使其不仅可以囚禁粒子,还可以旋转粒子。当涡旋光束与微粒相互作用时,涡旋光束的轨道角动量可以传递给微粒,导致微粒旋转,形成光学扳手。如图17所示,通过改变部分相干完美拉盖尔高斯光束的初始空间相干宽度、选择合适光束阶数,聚焦的部分相干完美拉盖尔高斯光束就可以同时捕获不同折射率的瑞利粒子。因此,可以使用一个光阱系统来捕获两种不同折射率的粒子[132]。

图17 不同参数下聚焦部分相干完美拉盖尔高斯光束对瑞利粒子的辐射力[132]Fig.17 Radiation forces of a partially coherent elegant Laguerre-Gaussian beam on Rayleigh particles with different parameters[132]

空心的光强分布使得纵向梯度力总是大于散射力的梯度力,因此可以在焦点处稳定地捕获高折射率的粒子。此外,部分相干涡旋光束中心光强较弱不仅能够稳定捕获低折射粒子,而且还可以有效减少粒子受到的热损伤。部分相干光可以多维度对光场实现调控,能够有效提升光学操纵效率,扩展光操纵的应用范围,在光学操纵中有重大意义。

5 分数阶涡旋光束

上述讨论均为拓扑荷为整数的情况,实际上,拓扑荷的值可以是非整数的。1995年,Basisty等[42]首次观测到涡旋光束的强度具有径向开口的现象,这是带有分数阶拓扑荷引起的,也就是分数阶涡旋光束。后来,人们对分数阶涡旋光束进行了大量的研究,包括分数阶平面波涡旋光束、分数阶高斯型涡旋光束和分数阶贝塞尔光束[43-47]等等。分数阶涡旋光束相对于整数阶涡旋在应用方面有一定的优势,在量子信息处理中,使用分数轨道角动量可以增加光子的纠缠度[48,49]。根据分数涡旋光束在光强分布上的特殊径向开口间隙,它既可用于光学分选,也可用于引导和传输粒子[4,50,51]。分数涡旋光束因为具有非对称光强分布,可用于实现各向异性边缘增强成像等[52-54]。分数阶涡旋光束在传输过程中光强与相位都是不稳定的,会发生光束旋转,相位奇点的分裂、产生和湮没以及拓扑荷跃变等现象,这些特性与整数涡旋光束有很大的不同。

2018年,Zeng等[55]又提出了一种兼具分数拓扑荷和低相干性的涡旋光束,即部分相干分数阶涡旋光束。研究了部分相干分数阶涡旋光束经薄透镜聚焦后的传输特性,部分相干分数阶涡旋光束最有趣的特性是光强的开口间隙和光斑的旋转效应随着传输距离的增加会逐渐消失,交叉谱密度分布随着相干性的降低而变得更具有对称性。

由于l是分数,很难推导出部分相干分数阶涡旋光束的解析传输公式,但是可以用数值积分求解[104]。部分相干分数阶涡旋光束通过ABCD光学系统的近轴传输可以用柯林斯公式来处理。图18显示了部分相干分数阶涡旋光束的强度分布,与部分相干整数阶涡旋光束的强度分布有很大的不同。部分相干分数阶涡旋光束的强度分布在源平面附近“甜甜圈”上有一个径向开口(z=0.1f),开口间隙随着z的增加而顺时针旋转(当l为负值时,逆时针旋转),并且在焦平面上旋转可达90°(z=f)。随着相干度σg的减小,焦面处的开口间隙分布逐渐消失,最终也变为高斯分布(σg=0.1 mm)。因此,当相干度σg较小时,在焦平面上很难区分聚焦的部分相干整数阶涡旋光束和聚焦的部分相干分数阶涡旋光束的光强分布。

图18 部分相干分数阶涡旋光束(l=1.5)在不同传播距离z后通过薄透镜聚焦的归一化强度分布[55]Fig.18 Normalized intensity distribution of a partially coherent fractional vortex beam(l=1.5)focused by a thin lens at several propagation distances z[55]

部分相干分数阶涡旋光束的交叉谱密度分布也与整数阶涡旋不同,从图19中可以发现,高相干度(σg=3 mm)的聚焦的部分相干分数阶涡旋光束的交叉谱密度的分布在源平面(z=0.1f)附近也有一个固有的开口间隙,它将在焦面(z=f)上旋转90°,交叉谱密度的分布旋转方向与光强旋转方向一致。另外,焦平面上的交叉谱密度的分布表现出横向对称性。随着相干度σg的减小和传输距离z的增大,交叉谱密度函数的分布逐渐趋于对称化,特别是焦面的对称性从σg=3 mm时的左右两侧对称演变为σg=0.1 mm时的矩形对称。可见,具有分数阶涡旋相位不仅会影响光强分布,还会影响相干度的分布。

图19 部分相干分数阶涡旋光束(l=1.5)在不同传播距离z后通过薄透镜聚焦的交叉谱密度分布[55]Fig.19 Density plot of the modulus of the cross-spectral density of a partially coherent fractional vortex beam(l=1.5)focused by a thin lens at several propagation distances z[55]

有趣的是,无论是分数阶高斯涡旋光束还是整数高斯涡旋光束,在源面上(z=0)的光强均呈高斯分布,关联结构也呈高斯分布,并且涡旋结构性质很难在源平面呈现,只有在传播时相干特性与涡旋性质才会逐渐呈现。而对于部分相干径向偏振分数阶涡旋光束[56],拓扑荷与相干度也会影响光束的统计特性。通过引入分数拓扑荷,部分相干径向偏振分数阶涡旋光束总光强与关联结构与标量部分相干分数阶涡旋光束分布类似,随着部分相干径向偏振分数阶涡旋光束的传输,光强变为径向开口的环形分布,并且随着传播距离增加,开口间隙逐渐旋转至90°。与标量部分相干分数阶涡旋光束不同的是,部分相干径向偏振分数阶涡旋光束带有偏振特性。例如,在近焦平面处,涡旋相位起到抗退偏振的作用;而在远焦平面处,随着拓扑荷的增加,涡旋相位首先起到退偏振的作用,然后起到抗退偏振的作用,因此它在偏振激光雷达系统中具有潜在的应用价值。部分相干径向偏振分数阶涡旋光束特殊的光强分布还可以用于同时捕获具有高折射率和低折射率的粒子。因此,通过适当地改变空间相干宽度,部分相干径向偏振分数阶涡旋光束可用来捕获具有不同折射率的粒子。此外,部分相干径向偏振分数阶涡旋光束具有固定径向缺口和自旋转特性的强度分布,可以实现光学分选。

对于常见整数阶拓扑荷的测量方法,如干涉法、柱面镜转换法、微扰法等,同样可以应用于测量分数阶拓扑荷,但是基本上都只能定性测量。对于分数阶涡旋光束拓扑荷的测量,如柱面镜转换法,分数阶涡旋光束通过相互垂直的柱面镜后也会出现与整数阶涡旋光斑类似形状。但是随着拓扑荷数小数的增加(例如从5.1增加到5.9),光斑强度分布会发生变化,而光斑个数不会发生变化,因此只能定性地分析拓扑荷大小而不能够定量测量。对于微扰法、双缝干涉法测量拓扑荷,通过相位的跃变也很难精确测出拓扑荷大小。2019年,Liu等[120]提出了一种深度学习方法来精确识别具有分数拓扑荷的涡旋光束,其中相邻模式识别的最小间隔可达到0.01,这也是第一次实现这种超高分辨率的拓扑荷测量。随着轨道角动量谱概念的提出,用轨道角动量谱表征分数阶涡旋光束的方法得到广大研究者的关注,通过测量轨道角动量谱将会对分数阶涡旋光束的测量带来更多可能性。

6 总结与展望

综上所述,对部分相干涡旋光束的理论模型、实验产生、拓扑荷测量、光场特性、以及分数阶涡旋光束等方面进行了简要综述。与完全相干涡旋光束不同,部分相干涡旋光束表现出一些独特的传输特性,如自整形、自修复等,这些特性对于粒子操纵、信息传递和超分辨成像具有重要的应用价值。与完全相干涡旋光束相比,部分相干涡旋光束在减少湍流引起的光束畸变和闪烁方面更具有优势,有望应用于自由空间光通信、光成像和信息传输。同时涡旋光束也是近年比较热门的课题,相信将二者结合将会有更多有趣的现象和潜在的应用。