轨道角动量光束中的经典光关联及其应用研究
2022-04-16孙亦凡陈天张卓孔令军张向东
孙亦凡,陈天,张卓,孔令军,张向东
(北京理工大学物理学院,北京 100081)
0 引言
在过去三十年间,科研工作者在量子信息科学领域取得了一系列重要进展,极大地拓展了人们对于信息编码和处理方式、传递途径、以及加密手段等研究课题的认识。概括地说,这些进展可以分为三个大类:1)以Shor算法及Grover算法等为代表的、优于现阶段已知的所有传统算法的信息处理过程,也即量子计算方案;2)以量子秘钥分发(QKD)方案为代表的、无法被现有的信息盗窃方法破坏的加密通讯过程,也即量子保密通讯方案;3)以双光子量子成像方案为代表的、突破经典测量精度极限的探测过程,也即量子精密测量方案。这些方案与20世纪上半叶形成的传统信息理论不同,它们以受量子理论约束的物态作为信息表示的出发点,以物态调控的手段作为信息处理的方式,实现了传统信息理论框架下难以完成的突破。例如,Shor[1]提出的质因子分解算法可以在多项式时间内求解大数质因子分解问题,该算法相对于传统已知最快的质因子分解算法存在指数加速效果,这样的特征实际上严重地威胁到了当前的加密安全性;Bennett和Ekert等[2-4]提出的量子通讯协议能够十分有效地对“窃听”行为进行侦测,规避了信息在不知情的情况下泄漏的风险,从而大大提高了通信过程的安全性。
量子信息优势的根源在于量子态观测结果之间特殊的关联关系。这些特殊的关联关系自量子力学理论诞生初期就被人们关注,围绕它们的讨论一直持续到今日。其中贯穿始终的是由Einstein等[5]开启的关于纠缠态的讨论。最初人们普遍认为,纠缠态是量子系统所独有的状态,并用可以区分纠缠态和非纠缠态的Bell不等式以及相关的判据作为区分经典系统和量子系统的标准。然而,近些年的一系列研究表明,对一些经典光学系统中的状态运用这些判据也可以得到与量子纠缠态类似的结果。例如,Spreeuw[6,7]指出了经典光的一些描述方法与量子态的数学形式之间存在良好的对应,并利用此性质进行量子信息过程的模拟。在该方案中,他提出了经典系统中与qubit对应的概念,将其记作cebit。除此之外,Kagalwala等[8]在研究光学相干性的时候也指出,当涉及不同种类自由度的相干性时,Bell型的测量也可以提供一个良好的相干性标定方式。从量子信息理论的角度来看,这样的研究结果说明量子信息中的优势原则上也可以通过上述经典光学系统展示出来。这意味着想要实现那些突破传统限制的信息过程,可能并不需要依赖脆弱的量子状态。事实上,人们沿着该思路也开展了大量的研究工作,并取得了一些重要的研究成果,本文将对相关结果进行介绍。
具体而言,本文集中展示了基于具有轨道角动量的光束的经典光关联过程,以及其在量子模拟、量子计算、以及量子探测方面的应用。实现一个信息过程的基础是恰当地选择能够对信息进行有效表示的物理自由度。事实上,光学角动量自由度在这一点上具有天然的优势。一个具有轨道角动量的光束,其轨道角动量状态原则上可以构成一组无穷维的线性正交基,因此其可以实现高维的信息编码。这为提升通信过程的信道容量[9]、优化信息处理方案[10,11]等提供了新的思路。将这样的特性与上述经典光学系统中的纠缠状态相结合,就可以实现对基于高维量子态的信息过程的有效模拟。
本文第1部分介绍了由轨道角动量状态和其他光学自由度构成的局域不可分离状态,并在第2部分总结了其在量子信息过程中的应用;第3部分介绍了空间可分的轨道角动量关联光束及其相关应用;第4部分介绍了基于轨道角动量光的随机行走,并讨论了此过程中展示的拓扑物理;最后进行了总结。
1 轨道角动量光束中的局域不可分离性
同一光束中不同自由度之间的与纠缠态相对应的关联关系,被称为局域不可分离性。这种不可分离性在早期被称为局域纠缠态,或非量子纠缠[6-8,12]。2015年,Karimi和Boyd[13]建议将上述经典状态的不可分离性在表述上与量子纠缠进行区分。他们强调,“纠缠”是在描述量子状态性质时所使用的术语,不应该与经典光学现象相混淆。因此,下文将这种状态称为不可分离态。
最早对经典不可分离态进行分析的研究之一是由Spreeuw[7]给出的。1998年,他以光束的偏振和路径状态为例,指出经典光场可以在表述形式上与量子纠缠态之间形成良好的对应关系。后来,Qian和Eberly[14]指出,对于更一般的偏振光场这种对应关系仍然存在,并且也通过Bell测量进行讨论。他们发现:在恰当定义测量的前提条件下,经典光也可以给出违反Bell不等式的“关联关系”。2013年,Kagalwala等[8]利用这种经典光的Bell测量讨论了涉及两种光学自由度时的相干性。通过Bell测量,他们对经典可分离光学自由度的相干矩阵所无法描述的状态进行了度量,发展了光学相干理论。
事实上,上述对不可分离状态的研究结果给出了一种模拟量子信息过程的方法。这样的模拟具备非常重要的特征,即量子信息过程在资源或者效率上的优势有希望被相对稳定且容易控制的经典光系统实现。原本在量子信息过程实现之前,人们需要先解决如何大幅提高量子系统的稳定性问题。现在,利用经典光学过程对量子信息过程进行模拟,人们可以很好地降低在维持系统稳定性方面的投入。最早指出光学局域不可分离状态可以用于量子计算的同样是Spreeuw[6],他定义了经典光学状态中与qubit相对应的状态,将其命名为cebit,并给出了一些简单的量子操作的对应关系,如CNOT门、Toffoli门的对应关系,以及量子纠错码中针对比特翻转问题的线路的实现等。这样的模拟在实验上确实较容易实现,但存在理论上的实现资源发散问题。随后,人们通过各种方法去丰富完善局域不可分离态的量子模拟方案,其中很重要的一种是引入高维的轨道角动量自由度。
作为量子模拟的基础之一,一个重要的问题是验证轨道角动量自由度可以用于构造局域不可分离态,并通过Bell测量来标定其“纠缠性”。一系列重要的工作完成于2000年之后,其中一部分整理罗列在表1中,有助于读者了解相关研究的进展脉络。Souza等[15]在早期关于光场拓扑相位的研究中,构造出了偏振自由度与轨道角动量不可分离的光学模式。这种经典光学模式中的一类特殊状态-一阶Hermitian-Gaussian模式与偏振状态,由Borges等[16]在2010年利用Bell不等式研究了其不可分离性,并得到了对不等式最大违背值2.1(大于经典极限2)。2015年,Song等[17]给出了基于整数轨道角动量光场与偏振不可分离模式的不可分离态的构造与验证。这样的状态可以用Spreeuw[6]的cebit记号写为
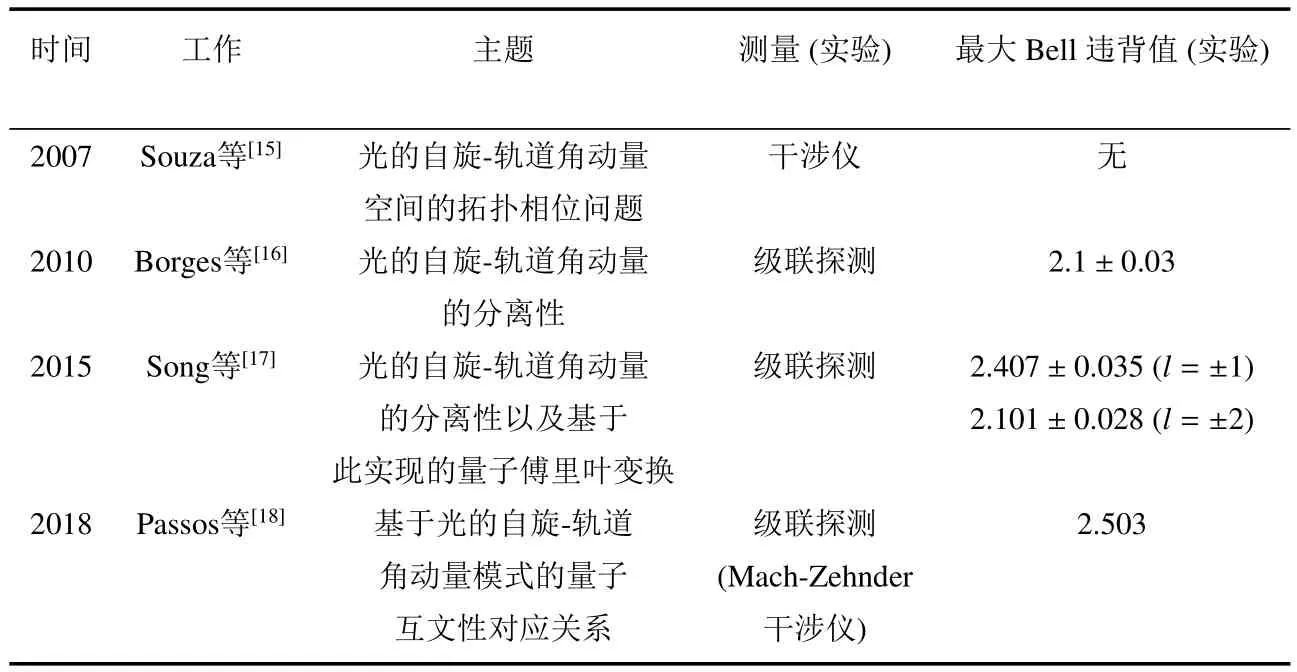
表 1 光的自旋(偏振)和轨道角动量不可分离状态研究简表Table 1 A brief review of the researches on the optical spin(polarization)and orbital angular moment non-separable states

与之前的工作类似,这样一个状态可以定义“关联测量”,即在经过偏振投影的情况下对光束的角动量状态进行分析。在此基础上,Song等对上述状态进行了Clauser-Horne-Shimony-Holt(CHSH)型Bell测量。在l=±1时,实验装置与结果如图1所示。其中图1(a)为实验装置示意图;图1(b)为实验结果图,实线和圆点分别为理论和实验结果,虚线标记的是出现最大违背CHSH型Bell不等式的地方。
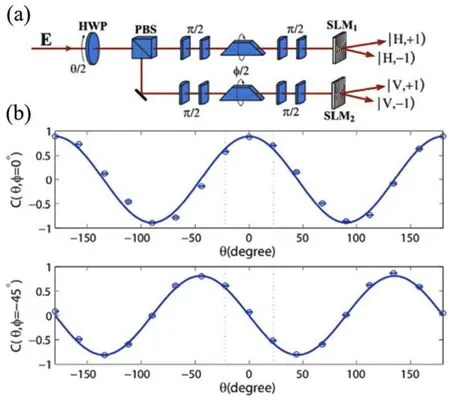
图1 (a)l=±1时不可分离态CHSH不等式验证实验装置及(b)关联函数曲线[17]Fig.1 (a)The experimental setup for observing the violation of CHSH inequality based on the non-separable states when l=±1 and(b)the correlations[17]
另外,Song等[17]还考虑了l=±2的情况,并用另一种实验方案进行了CHSH型Bell测量的实验,如图2(a)所示。这种方法主要利用光学偏振自由度和轨道角动量之间天然的“相互作用”实现对角动量状态的调制,并通过干涉仪完成对状态的测量[17],实验结果展示在图2(b)。取φ′=±π/8,θ′=0,-π/4,此时的最大Bell违背值B=2.101±0.028。与l=±1方法的结果对比,可以发现图2所示方法对Bell不等式的违背情况出现了“减弱”,这是实验操作的精度不足所致。并且,在对状态(1)的研究中,这种对精度的要求会随着l的增加而提高。但是,CHSH型Bell不等式违背的情况最终还是可以确认的。
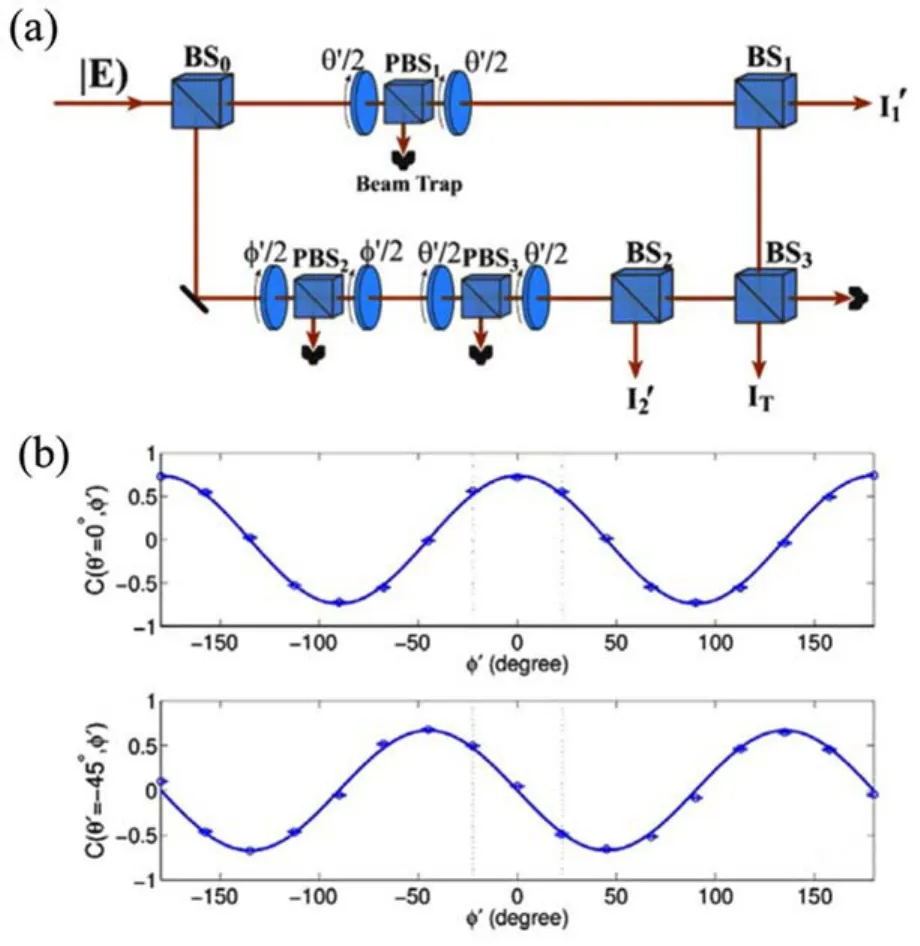
图2 (a)|l|=2(同样适用于|l|>2的情形)时不可分离态CHSH不等式验证实验装置及(b)关联函数曲线[17]Fig.2 (a)The experimental setup for observing the violation of CHSH inequality based on the non-separable states when|l|=2(also suitable for the cases when|l|>2)and(b)the correlations[17]
上述结果与Spreeuw、Eberly、Kagalwala以及表1中列出的研究工作结论相吻合,验证了轨道角动量光束中的局域不可分离性,这为实现基于光学角动量状态的量子信息过程提供了重要的基础。实际上,人们以此为出发点开展了一系列关于角动量不可分离态的应用研究,下文将对几个具有代表性的工作进行逐一介绍。
2 基于偏振和轨道角动量的局域不可分离态在量子信息中的应用
首先介绍轨道角动量不可分离状态在量子计算方面的应用。2005年,Oliveira等[20]提出用偏振态和横向空间模式构造出的量子Deutsch算法,是该领域早期的重要工作之一。2007年,Deng等[21]指出偏振与轨道角动量之间的关系可以用于构造量子CNOT门,这为利用不可分离态进一步实现更广泛的功能性量子算法奠定了基础。2015年,Song等[17]设计了轨道角动量和偏振不可分离态的Hadamard门和受控相位门,还在实验中实现了对两qubit系统量子Fourier变换(轨道角动量l=±1)的模拟,如图3所示。其中轨道角动量Hadamard门由道威棱镜和柱透镜组合构成,CPhase门由螺旋相位片(SPP)和空间光调制器(SLM)构成,偏振的Hadamard门由半波片实现。与通常量子实现的量子傅里叶变换(QFT)相比,经典的QFT实现方法简单,易于操作,且测量效率很高。这对于实现量子计算的经典模拟来说至关重要,因为量子Fourier变换是量子计算中Shor大数分解算法中最重要的一步,也是Shor算法优于同类经典算法的主要原因[22]。Song等[17]的研究工作有望成为经典和量子信息过程对应的重要参考。
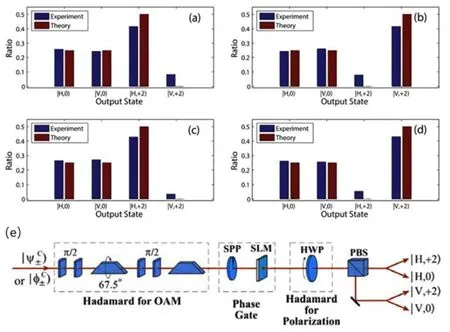
图3 (a)~(d)由轨道角动量和偏振构成的不可分离态经过QFT实验的输出结果与理论结果对照以及(e)实验采用的光路图[17]Fig.3 (a)~(d)Comparison between the experimental results of the states output by the QFT setup with different input OAM-polarization non-separable states and the corresponding theoretical results,and(e)the optical scheme[17]
在量子通信领域,量子隐形传态是纠缠的重要应用之一,由Bouwmeester等[23]首次在光学量子纠缠态系统中实现。基于不可分离态的性质,Hashemi Rafsanjani等[24]提出:可以使用相干激光的两个自由度来替换纠缠光子对,然后通过执行Bell测量使其中一个自由度携带的信息传递到另一个自由度,从而达到用经典光模拟量子隐形传态的效果。在他们的实验方案中,最核心的关联关系是轨道角动量和偏振自由度构成的不可分离态。为了实现传递信息的功能,他们考虑的第三个自由度是径向自由度,实验装置如图4所示。SLM1和Bell态合成器用于制备角动量态的角向和径向模式的最大纠缠态,并通过SLM2实现其Bell测量;针孔用于分离上一步的“投影测量”结果;最后通过波片(QWP与HWP)完成了偏振态的分析。最终他们实现了将偏振态转移到光场横向模式,也即轨道角动量模式的状态转移过程。与之类似的一个实验在2016年由Pinheiro da Silva等[25]完成。与Hashemi Rafsanjani等的工作不同的是,该工作考虑的第三个自由度是路径自由度。
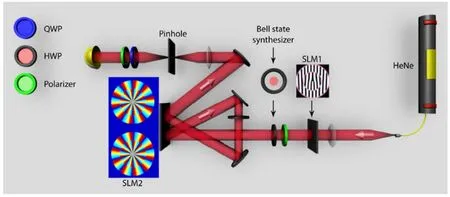
图4 局域自由度状态转移实验方案示意图,主要实现轨道角动量状态到偏振状态的“状态转移”(对应量子隐形传态方案)[24]Fig.4 The experimental realization of the state transfer in the local degree of freedom.In such a setup,the state of OAM is transferred to the state of polarization(corresponding to the quantum teleportation)[24]
轨道角动量的一个重要特性是维度高,这使它可以实现密集编码。使用这种编码方案仅对纠缠光子对中的一个光子执行局域的操作,就可以实现信息编码的过程。与之对应的解码过程用Bell测量实现,这等同于提高了单个光子所能携带的信息量。2015年,Milione等[26]利用矢量光束轨道角动量和偏振自由度的不可分离性在光通信中实现了密集编码。首先,Milione等通过实验证实矢量光束的不可分离性可用于光通信中编码信息,他们使用传统的波片对矢量光束不可分离态的偏振自由度执行四种操作(单位算符和3个Pauli算符),成功地编码了2 bit的信息。由于执行操作后得到的四束矢量光的状态与纠缠光子对的4个Bell态相对应,所以对这四束矢量光的识别实际上等同于密集编码方案的解码过程。事实上,观测输出光束在CCD相机上的空间位置就可以识别这四个态。此外,他们的研究还表明,使用包含高阶Pancharatnam-Berry相位和液晶q板的Mach-Zehnder干涉仪可以以低至2.7%的串扰有效地解码矢量光束。同年,Milione等[27]基于同样的矢量光束构造实现了自由空间中的信息传输,其传输效率达到了4×20 Gbit/s。这项工作的优势在于仅需对不可分离态的偏振自由度执行操作就能够访问光的偏振和空间自由度构成的四维态空间,这意味着仅操作偏振自由度就可以编码2 bit的信息。但问题在于,偏振自由度被它自己所固有的二维Hilbert空间所限制,这导致态空间的维数不能进一步提升。
为了进一步提升态空间的维数,从而打破偏振自由度带来的固有限制,2016年,Li等[28]提出了一种基于杂化矢量光束的偏振和轨道角动量自由度之间的不可分离性实现的多进制编码协议。这种编码方案主要基于改进的偏振Sagnac干涉仪,利用偏振自由度对光束的轨道角动量自由度执行变换,从而实现高维空间的信息编解码过程,这使得可以仅通过操纵N/2个不同的轨道角动量模式来实现N维不可分离基矢的N进制编码,也即编码log2Nbit的信息。实验结果还表明矢量光束的解码可以以很低串扰的形式实现。与转换标量光束的轨道角动量模式的编码协议相比,Li等提出的基于矢量光束经典不可分离性的编码方案,在轨道角动量模式数量相同的情况下能够编码更多的信息,这能够很好地解决随着轨道角动量量子数的增加而产生的传播发散问题,并且实现了四进制和十六进制的编解码。此外,在相同的初始强度分布下,矢量涡旋光束在自由空间光通信中表现出了比标量涡旋光束低得多的闪烁[29],这意味着可以通过使用矢量光束携带信息来减轻大气的影响。因此,Li等的方案在许多实际情况中具有潜在的应用,这对光通信而言有很大的益处。下面给出一些具体的理论描述。
杂化矢量光束由两个正交的线偏振以及大小相同但符号相反的拓扑荷叠加构成。具有单位振幅的杂化矢量光束的态可以写为

式中:|±l〉代表轨道角动量模式,|H〉和|V〉分别代表水平偏振和竖直偏振,⊗代表张量积。θ决定两自由度的权重,当θ≠0°以及θ≠90°时,(2)式表示的态不能分解为两自由度态的直积,这说明两自由度之间的不可分离性或者说耦合强度与θ有关。尽管(2)式采用了Dirac符号,实际上也可以通过经典光场实现该状态,其性质与量子光场并无大异。Li等主要通过利用经典光场构造状态完成了下列实验。
两自由度之间的不可分离性可以通过偏振相干度Dpol以及轨道角动量模式相干度DOAM来进行量化,其中Dpol可以表示为


可见Dpol是θ的函数,与(1)式中两自由度之间的不可分离性对θ的依赖关系相一致。当θ=45°时耦合强度最大,对应着最大不可分离态;当θ=0°或θ=90°时,杂化矢量光束的态实际上是可以分离的,即表示成两自由度态的直积。
不可分离态的另一个重要特征是,两个自由度的投影测量结果之间并不独立[30,31]。定量而言,考虑将偏振投影基写为

式中γ和ε分别对应Poincar´e球面上一点的经度和纬度。接着,把杂化矢量光束态往偏振投影基|Ω〉上投影。从计算结果可以看出,当初态可分离时(θ=0°或θ=90°),(5)式对应的光束空间模式与投影基矢|Ω〉无关。相反地,对于不可分离态,特别是最大不可分离态(θ=45°),最终得到的态的强度分布与偏振投影基矢|Ω〉有关。
与Milione等[26]不同的是,Li等[28]操控的是轨道角动量这一自由度,于是能够实现在一个更高维度的态空间进行信息编码,下面详细描述编码实验过程,考虑一个最大不可分离态

当l=1时,构成矢量光束的两部分|l〉|H〉以及|-l〉|H〉的光束强度和空间偏振分布如图5(a)所示。编码过程通过对轨道角动量模式自由度的幺正变换来进行。首先,编码者Bob把单位算符0和三个幺正算符应用到矢量光的轨道角动量模式,这里的4个算符定义为
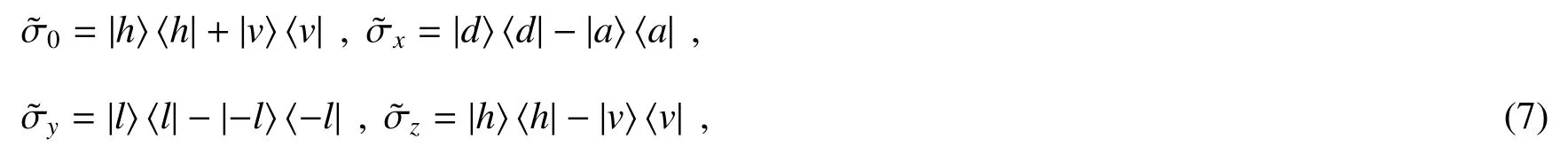
式中|h〉和|v〉为轨道角动量基矢,与线偏振基|H〉和|V〉等价。同理,|a〉和|d〉与±45°偏振基对应,具体的定义为
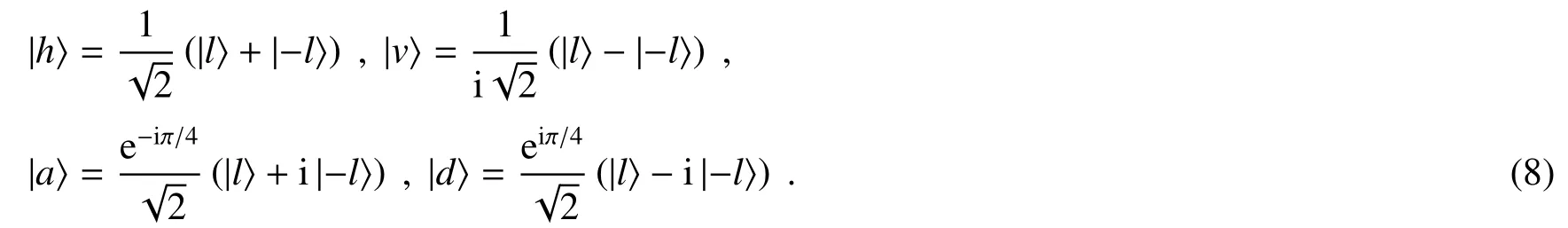
于是,最初的不可分离态可以通过上述变换转化为四种矢量光束对应的正交状态之一,从而实现编码过程。图5(b)展示了将单位算符0以及三个Pauli算符作用到上之后得到的矢量光束的空间与偏振分布。除了上述方法,还可以利用轨道角动量空间无穷维的性质来产生更多可用于编码的状态。为了保证所产生矢量光束的态彼此是相互正交的,编码者Bob需要执行自旋受控门操作,即

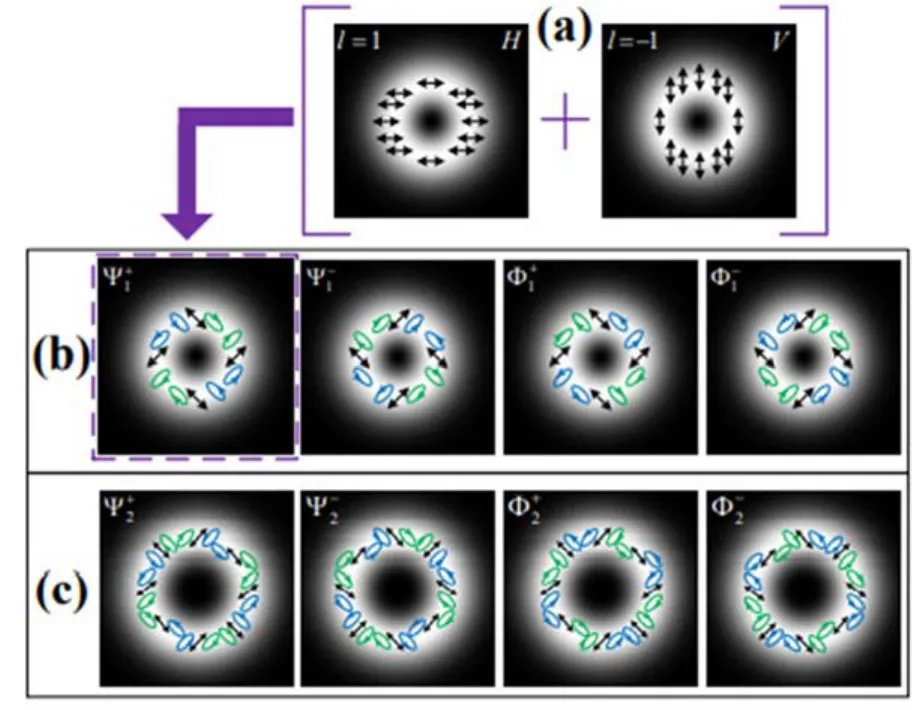
图5 矢量光束偏振结构示意图。(a)l=1时的OAM与偏振不可分离态矢量光束;(b)单位算符0和三个Pauli算符x、y、z操作后得到的矢量光束的偏振结构分布图;(c)l=2情况下经过(b)同样操作得到的矢量光束的结果[28]Fig.5 Polarization distribution of the vector beam.(a)OAM-polarization-non-separable state when l=1;(b)The polarization distribution of the vector beams after being operated by the identity operator0and three Pauli operatorx,y,z;(c)The similar case to(b)except for l=2[28]
新的矢量光束的态可以写为

图6展示了Li等[28]设计的基于经典不可分离性的高维编解码实验装置,分为制备、检测、编码(Bob)以及解码(Alice)四个部分。他们使用矢量光束的态来编码四进制数1→4,Bob对矢量光的轨道角动量自由度应用单位算符0以及三个Pauli算符。在如图6所示的四个输出口A1、A2、B1和B2,输出光束的强度主要通过透镜、针孔等配合功率计进行测量得到。这种方案具有低串扰(<6.6%)的优点,该方案与量子密集编码相对应。杂化编码的部分结果展示在图7中。
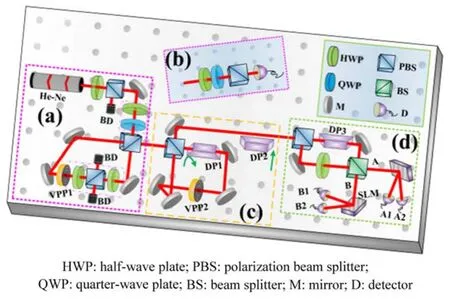
图6 基于具有经典不可分离性的矢量光束的高维编码/解码实验方案。(a)光束的制备装置;(b)实验测量装置;(c)编码过程(由Bob完成);(d)解码分析(由Alice完成)[28]Fig.6 The high dimensional encoding/decoding scheme based on classical non-separable state of vector beams.(a)The setup for generating the beam;(b)The setup for measurement;(c)The encoding process(by Bob);(d)The decoding process(by Alice)[28]
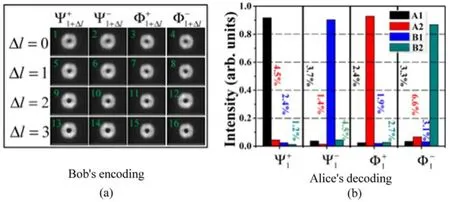
图7 (a)利用杂化矢量光束进行杂化编码的结果,包括四进制和十六进制情况;(b)对矢量光束的OAM自由度进行单位算符0以及三个Pauli算符x、y、z的操作后,四个输出口的输出光场强度图,图中百分数为串扰[28]Fig.7 (a)Results of encoding using hybrid vector beam,including the quaternary and hexadecimal case;(b)Intensity of light output by the four ports after the modifications on the OAM degree of freedom.The modifications are described by the identity0and the three Pauli operatorsx,yandz.The percentages in the figure give the cross talks[28]
基于上述方案的框架,也可以实现十六进制的编码,这需要在实验装置中两个空间光调制器上都加载一个拓扑荷的叉形二进制光栅来进行解码。同样地,在功率计前放置了针孔进行空间滤波。归一化后,模式串扰最高为13.6%,仅需要八个轨道角动量模式就可以实现十六进制的编解码。
实现上述四进制和十六进制编解码的方案均使用了具有最大不可分离态的矢量光束,也即两个自由的处于耦合最大的状态。那么耦合程度如何影响编码和解码过程呢?Li等[28]以四进制编解码为例给出了对应的结果。实际上,在(2)式的矢量光束状态中,所谓的耦合强度可以通过角度θ进行调节。对不同θ的矢量光束作为初始态的情况,他们依然设置Bob和Alice分别按照之前所述的方式进行操作,实验结果展示在图8中。由图8可见,随着轨道角动量与偏振自由度时间不可分离性的下降,不同模式之间的串扰逐步增强,这导致了获取信息的准确性不断下降。以θ=0°、θ=15°、θ=60°和θ=90°为例对耦合强度产生的影响同样展示在图8中[28]。模式串扰的大小依赖于矢量光束不可分离性的强弱,特别是θ=0°或θ=90°(耦合强度为0,两自由度可分离,光束没有矢量特性)时,模式串扰高达47.9%,这直接导致Alice只能识别两种信息,也就是说,只有1 bit的信息被编解码。因此,与基于可分离态的编码方案相比,基于不可分离态的编码方案能实现信息量两倍的增长。
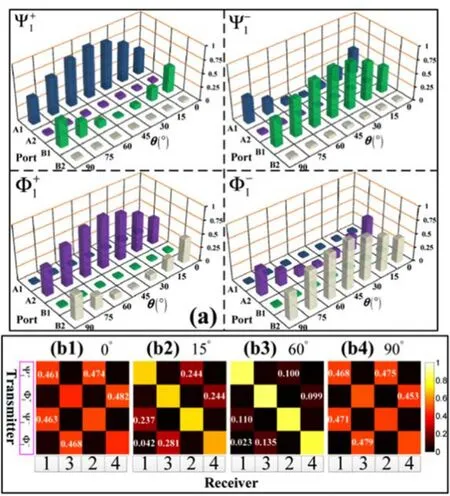
图8 (a)四进制编码的解码情况随耦合强度的变化关系图。θ=45°时为最大耦合,θ=0°或θ=90°为最小耦合;(b)四进制编码和解码过程的串扰矩阵。(b1)~(b4)分别对应θ=0°,θ=15°,θ=60°和θ=90°的情况[28]Fig.8 (a)Decoding results of the quaternary encoding scheme,changing with the coupling strength.The coupling strength reaches its maximum when θ=45°,and reaches its minimum when θ=0° or θ=90°;(b)Crosstalk matrix of the quaternary encoding scheme.(b1)~(b4)are the cases when θ=0°,θ=15°,θ=60°,and θ=90°,respectively[28]
前面所介绍解码过程的实现思路主要是通过空间光调制器对输出光场进行调制,将其转化为可通过中心亮斑位置来区分的状态。实际上,这样的解码方式在经典通信中已经被广泛使用。但其缺点也是明显的,即不能同时展现出所有矢量光束编码在相位上的差别,并且需要不断地根据测量的需求改变空间光调制器的图样。如果引入一个复合光栅全息图[28],就能够同时识别携带不同信息的入射光。例如,文献[28]的全息图为生成l=1和l=3的相位图的叠加,它们能够分别产生水平和竖直的衍射光束。在分别过滤掉除去一阶衍射光以外的光场后,就能够得到一个3×3的衍射图样,因此可以同时测量9个不同的轨道角动量态。除去图像的中心部位,其它的16个区域分别与解码前的16个矢量光束相对应,因此该方案可以应用于进行十六进制编码的解码。相关实验结果表明模式串扰达到了8.3%,相对较大,可能是实验方案未经过充分优化导致。尽管利用复合光栅可以进行包含16个矢量光束的分析和探测,但这样的探测实际上相对较窄。除此以外,还可以考虑应用集成的5×5二进制Dammann涡旋光栅,其探测范围可以达到-12~+12的轨道角动量光束,因此有望实现32进制的编码与解码。
值得一提的是,除了上述量子信息过程模拟上的应用,局域不可分离态还有一些其他有趣的应用。2014年,Töppel等[32]使用不可分离态来测量光学偏振,并指出与传统的偏振测量相比,这种测量可以一次性获得更多的状态信息。他们还提出并展示了一种基于涡旋光束经典纠缠检测高速运动物体位置和方向的方案[33],测量原理依赖于涡旋光束中横向空间模式与偏振自由度之间的固有关联。仅需对几个快速光电二极管执行强度测量就可以实现固有关联的测量,而且在带宽方面远远优于当前的CCD和CMOS器件,最终实现了GHz分辨率的二维实时传感。
2017年,Ndagano等[34]使用经典光的不可分离态来表征量子信道质量。引入光场的空间模式自由度实际上有望增加量子信道的安全性和容量。但不幸的是,微扰会导致纠缠衰退,从而导致量子关联不可修复的破坏,如果不对信道进行量子层析成像,就无法修复这些关联。与之矛盾的是,如果没有一个可用的关联,就无法实现信道的层析成像。为了解决这个问题,Ndagano等提出了一种鲁棒的方法,使用经典光来表征量子信道质量。他们以湍流大气中的自由空间通信为例,证明了经典纠缠态的演化与量子纠缠态的演化是等价的,从而为经典纠缠的概念提供了新的物理见解;他们用经典光实现了对量子信道的实时分析,根据纯态轨迹理论解释了随机动力学。这使得无论是短距离和长距离光通信,亦或是自由空间光学和光纤光学,精确的量子纠错都可以参考上述方法实现。
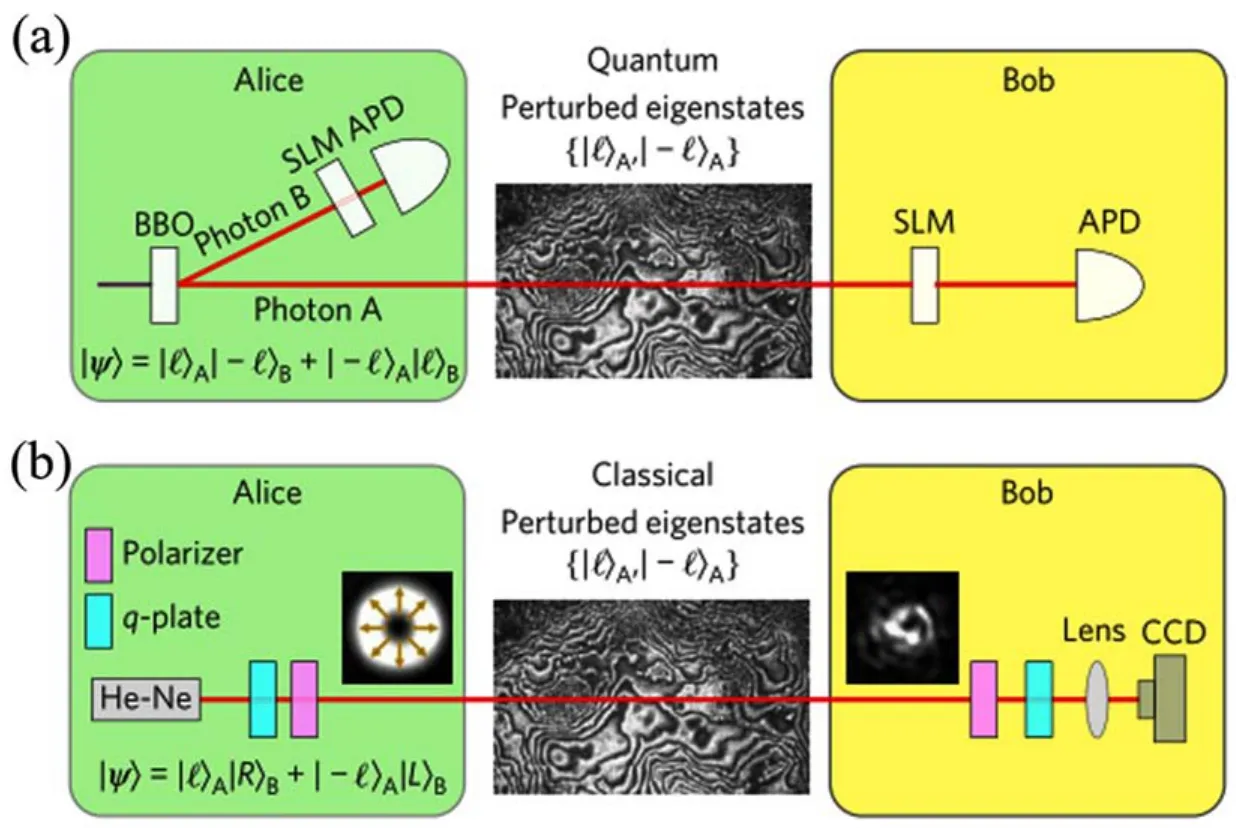
图9 利用不可分离态进行量子通道测试的方案示意图。(a)量子通道的展示;(b)与(a)对应的经典不可分离态检测方案[34]Fig.9 Schematic illustration of qualifying the quantum channel using non-separable classical state.(a)Illustration of quantum channel;(b)Qualification of the quantum channel corresponding to(a)[34]
Otte等[35]基于自旋和轨道角动量的耦合实现了自由空间的纠缠律动。众所周知,量子态的纠缠在局部幺正变换下具有不变性,这意味着当光子在自由空间传播时,其内部自由度之间的纠缠应该是保持不变的。但Otte等在他们的实验中观察到了不同的现象,即纠缠是变化的,其变化情况如图10所示。他们利用具有不可分离自由度的经典矢量涡旋光束,证明了传播过程中的局域不可分离态是变化的,其会在最大纠缠态和直积态之间振荡。他们描述了这些新奇传播特性背后的自旋轨道相互作用,并通过实验证明了旁轴光束中的自旋轨道耦合。此证明给出了一个重要的经典不可分离态特性,同时提供了一个可以按需向目标传递矢量光束的装置。这对于动态激光材料处理、受激发射损耗(STED)系统的分辨率提升、以及纠缠的牵引光束设计均十分有益。
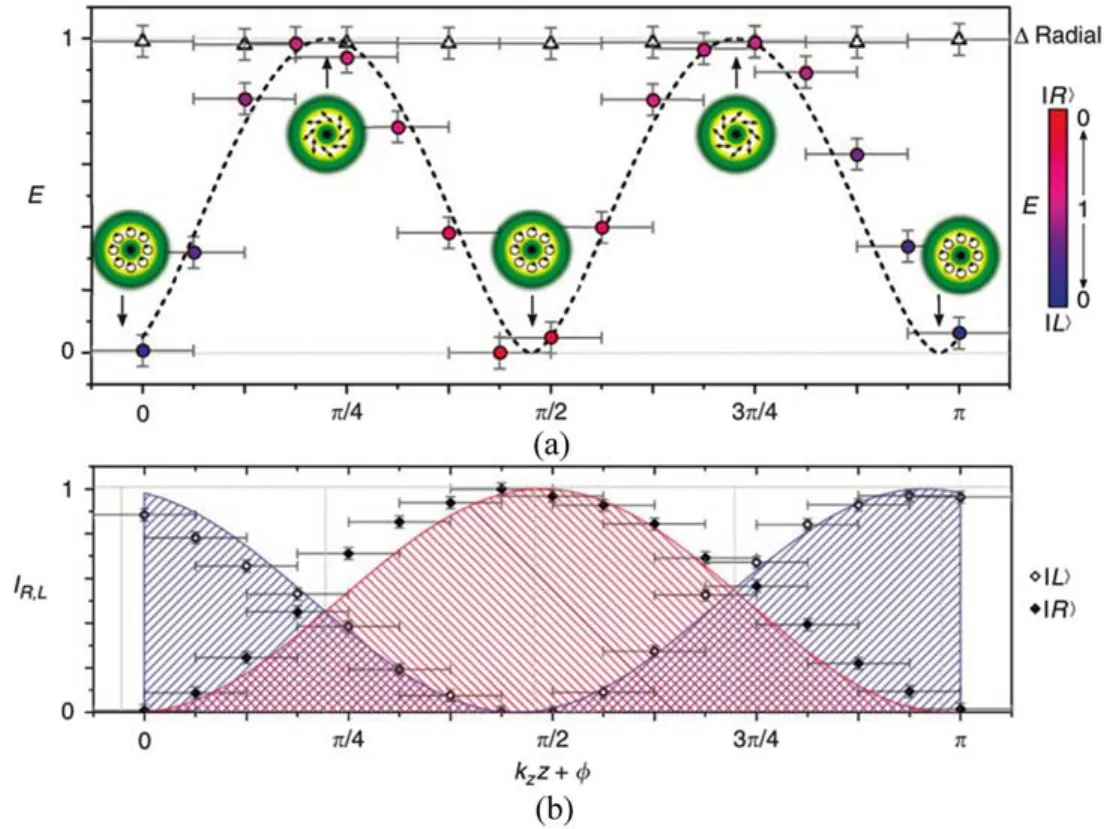
图10 局域不可分离态光束在传播过程中的关联关系变化图。(a)径向模式分析;(b)左旋和右旋偏振分析[35]Fig.10 Evolution of the correlation of non-separable vector beam in propagation.(a)Analysis of radial modes;(b)Analysis of the left-handed and right-handed circular polarization[35]
上述内容回顾了局域不可分离态与量子Bell态之间的对应关系,以及以此为基础建立的量子模拟等应用。这些结果表明:经典光束的不可分离态,特别是轨道角动量态,可以完成和量子信息过程相对应的任务,并且具有良好的稳定性。最近在局域不可分离态和轨道角动量的研究中,也取得了一系列重要成果。例如,Shen等[36]利用具有空间分布的偏振光场实现了GHZ态的模拟,为实现基于局域自由度的多“粒子”纠缠形式提供了很好的思路;Liu等[37]通过引入拉盖尔-高斯光束的径向模式,实现了高维的局域不可分离态;而相关的量子光实验由Bouchard等[38]完成。除了与局域不可分离状态直接相关的研究,轨道角动量在其他问题上也提供了不错的应用。例如:在通信方面,Ding等[39]提出了一个宽带的角动量光子与存储器之间的转化界面实现方案;在量子模拟方面,Clark等[40]利用轨道角动量态与Rb原子的相互作用,实现了光的Laughlin态;Wang等[41]提出了一个利用经典结构光场实现对相干态的模拟方案,等等。局域不可分离态中的关联关系主要依赖自由度之间的耦合。这种耦合对于光束来说是天然的,但不能将其在空间上进行分离。量子信息过程一个重要的特点是利用纠缠态的非局域性来实现通信协议,这对于局域不可分离的自由度而言是无法实现的。于是,在经典光学系统中实现对非局域纠缠态的模拟就成为了一个重要的研究课题,接下来将总结回顾相关研究中一些重要的研究成果。
3 空间可分离轨道角动量光束中的经典光关联
在关于空间可分离关联光束的研究中,有两个重要的实验工作。一个是Lee和Thomas[42]于2002年提出的基于后选择方法模拟量子纠缠的方案。他们实验上用包含两种频率和两种偏振的经典场模拟两个纠缠的qubit,以两个空间区域分离的光外差节拍信号的倍增来模拟两粒子的符合检测,这样获得的信号包含若干频率分量。他们通过带通频率滤波挑选出其中一个信号,获得的带通信号包含两个部分,对这两个部分进行设置能够模拟出四个偏振纠缠类Bell态。Lee和Thomas提出的经典场方法[42,43]能够直接模拟线性光量子实验的高阶干涉。另一个工作是Sun等[44]利用非相干光源得到的EPR关联光束实验。他们在实验中利用两束包含非相干光学成分的光束作为光源,以光场的一阶关联强度作为衡量标准,得到非局域EPR类型的经典关联。以此为基础,他们进一步实现了对空间可分离的量子隐形传态实验的经典对应。
不同于局域光束的不可分离态,以上两个实验模拟的是多粒子纠缠,也即EPR类型的纠缠。这实际上意味着在经典系统中也可以找到具有与量子非定域性相对应的系统或者结构。因此,在量子信息理论中依赖非定域性构建的信息处理方案也有望通过经典光学系统实现。与局域不可分离态类似,考虑到使用经典光可获得的稳定性和高信噪比,以及产生类似于量子系统观测的潜力,利用这种方式来进行量子模拟研究同样颇有价值。
接下来介绍一个空间可分离轨道角动量光束的实现方案,并给出其在非局域密集编码中的应用。基于量子非局域性的密集编码方案由Bennett和Wiesner[4]于1992年提出的。2016年,Yang等[45]实验上实现了量子密集编码的经典模拟,他们的方案如图11所示。与使用偏振纠缠光子对的量子密集编码相比,他们提出的设计显示出了许多优点。基于12个四进制的数而不是通常的24 bit传输ASCII码的密集编码实验可获得高达2 bit的信道容量,高于通常的量子编码容量1.585 bit。这种方案在光通信中的实现比较方便,还可以从探测器直接识别出信息,而不是像量子情况一样需要干涉和符合测量。并且,此种经典方案可以直接应用于目前的通信系统,相较于传统通信方案可以提供更具潜力的通信过程。
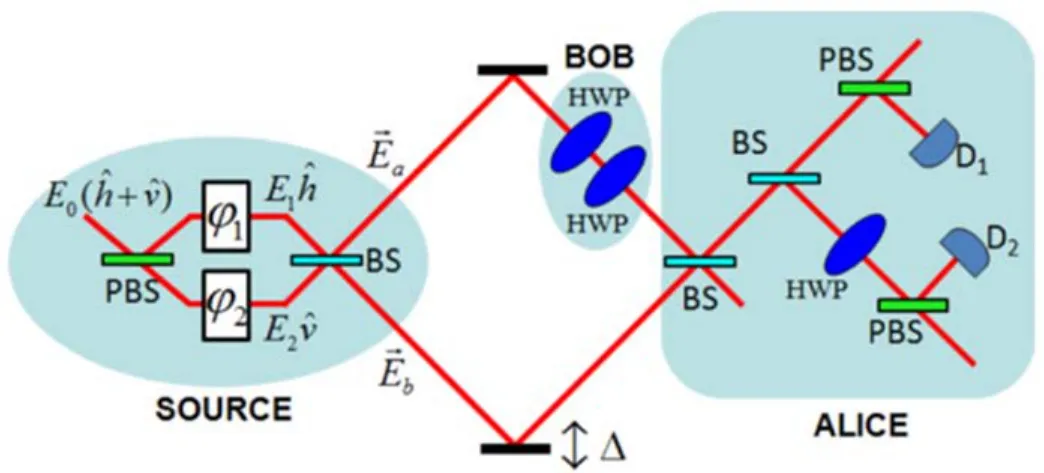
图11 空间可分离经典光模拟密集编码实验方案示意图[45]Fig.11 Scheme of dense coding based on the spatially distinguished beams[45]
除了密集编码以外,还有编码信息量更大的超密编码方案,这样的方案主要基于超纠缠态。早在2005年,Barreiro等[46]就制备出了超纠缠的光子对,他们第一个在实验上制备出了每个自由度都有纠缠的量子系统。利用自发参量下转换产生的纠缠光子对,他们通过测量每个自由度(包括偏振、空间模式和时间能量自由度)Bell不等式的违逆情况来证实这个自由度的纠缠。并且,他们还生成并表征了最大超纠缠态以及同时表现出量子关联和经典关联的新态。除此之外,Barreiro等[47]还对一个2×2×3×3的系统(36维希尔伯特空间)执行了层析测量,这是第一个报道的采用该表征方式对这种大小的光子纠缠系统进行表征的实验。
Li等[48]第一个实现了经典超关联和基于经典光的量子超密集编码的模拟。在Li等的经典超关联实验中,光束的每个自由度都是同时相关的,也即可以观察到每个自由度的关联函数违背Bell不等式的现象。基于这样一种经典超关联,Li等在经典光学中实现了量子超密集编码的模拟。与基于同时处于偏振和非偏振纠缠态的光子对的量子超密集编码相比,经典方案具有许多优点。该方案不仅实现起来较为方便,而且可以获得单通道3 bit的信道容量,高于量子方案的2.8 bit。同经典密集编码方案类似,该方案可区分的信息也可以直接从探测器识别,不需要干涉和符合测量。
制备经典光超关联态的实验装置如图12所示,该装置分为制备和表征两部分。产生经典超关联态的源由两个完全非相干光束构成,它们的光场分别记为E1和E2,满足条件这里r和t分别代表空间坐标和时间。两个完全非相干光束分别来自两个独立的波长为632.8 nm的氦氖(He-Ne)激光器,他们各自通过一个螺旋相位片(SPP)转变为涡旋光束。随后用一个偏振分束器(PBS)将光束进行汇集,得到包含了水平极化的E1和竖直极化的E2光场。该光束通过一个改进的Mach-Zehnder干涉仪,干涉仪中一个干涉臂的反射镜主要用于轨道角动量模式相位翻转(将正的螺旋转化为反向的螺旋)。实验中取l=2,一个可变相位延迟器(LCVR)的插入是为了确保两臂光束的非相干性。为了分析Ea(r,t)和Eb(r,t)之间的超关联特性,Li等在实验中将生成的两束光分成两部分。一部分用来执行偏振关联的验证,另一部分用来执行轨道角动量关联的验证。类似于量子超纠缠关系的验证实验,上述操作主要是为了避免不同自由度之间的纠缠关系产生相互干扰[46]。
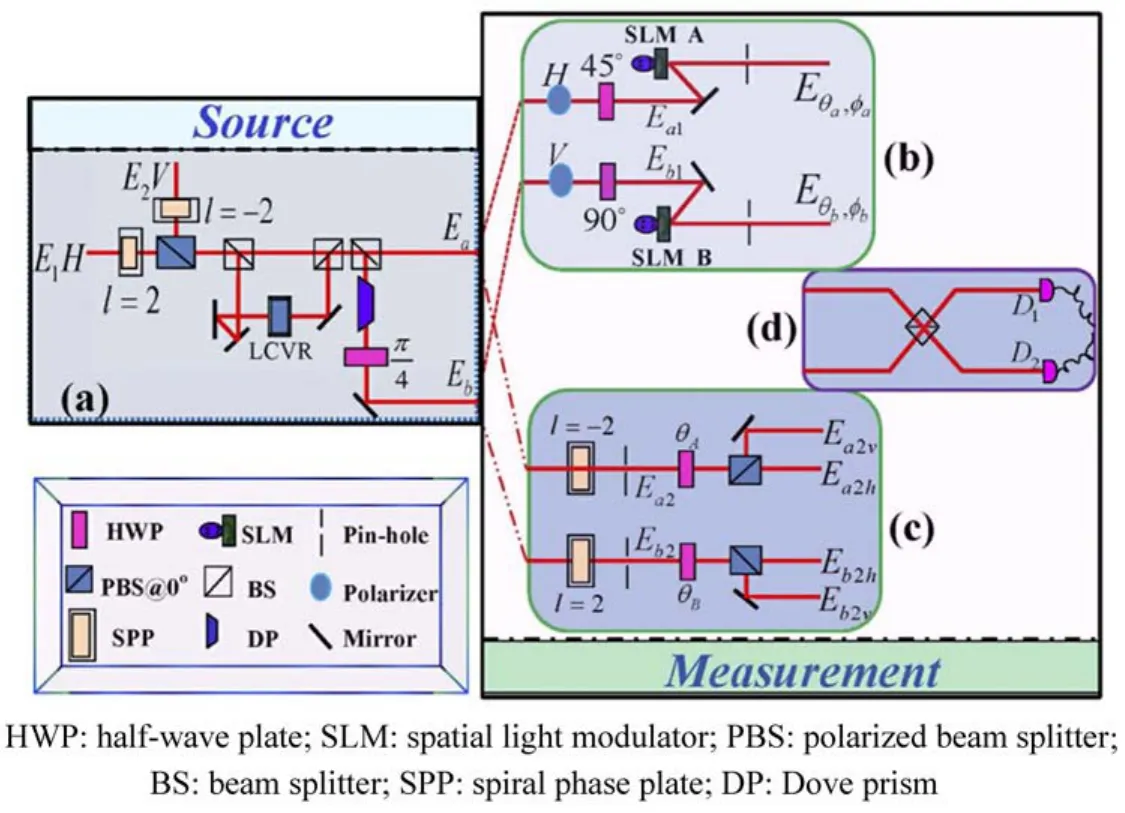
图12 经典超关联实验方案。(a)超关联源的装置示意图;(b),(c)分别对应OAM和偏振的关联测量装置;(d)场的一阶关联测量的原理示意图[48]Fig.12 Classical super correlation experiments.(a)Setup of the source;(b),(c)Measurement setup of OAM correlations and polarization correlations,respectively;(d)Setup for measuring the first-order correlation of the fields[48]
与经典局域纠缠一样[17],为了量化Ea(r,t)和Eb(r,t)之间的关联关系,Li等同样执行了CHSH不等式的测量,关联函数定义为
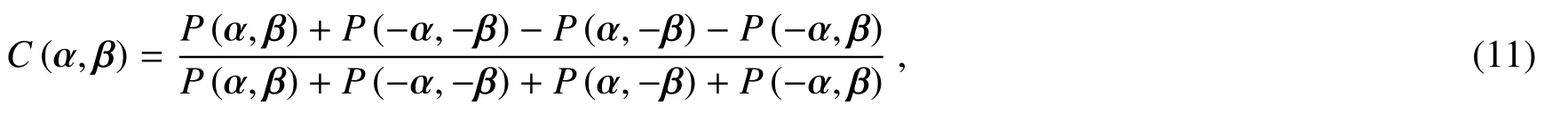
式中P(α,β)为在某个测量基下的关联概率,由光场的一阶关联函数给出[44]。
根据一阶关联的定义,光场的一阶关联和可以通过先记录光场的完整信息,然后通过类似示波器的装置进行信息处理后得到,实际上这样的方法并不容易实现。图12的方案中,Li等使用的是一种间接处理方式。他们通过一系列操作分别得到一阶关联的实部和虚部,然后执行CHSH型的Bell测量
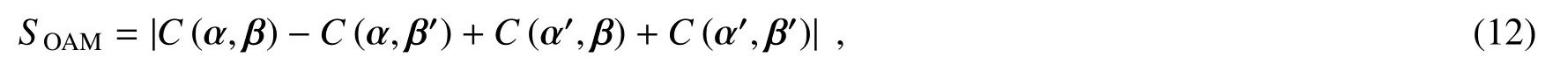
式中α和β代表了两组不同的测量基取向,分别通过设置SLM A和SLM B上的图样来进行调节。图13(b)展示了归一化的关联概率,每条曲线都是θb和φb的函数,这两个参数决定了SLM B上加载的全息图。四条曲线分别对应图13(a)左中标示出的四个态。图中的点代表了实验结果,实线对应理论曲线,两者吻合得很好。实验结果的对比度达到了91.93%,完全满足出现违背Bell不等式所需要的条件(大于70.7%)[49]。实验误差的主要来源是干涉仪不稳定导致的失谐,由图13(b)中的误差棒展示出来。具体而言,当θb=π-θa且φb=φa时关联强度达到了极大值;相反,当θa=θb且φb=φa+π时,关联强度达到了极小值。由图中数据计算可以得到:当θa=0、φa=0、θ′a=π/2、φ′a=π、θb=3π/4、φb=π、θ′b=π/4以及φ′b=π时,可以得到|SOAM|max=2.756±0.017。正如局域隐变量理论所给出的,Bell参数的最大值|SOAM|max<2,因此,Li等的实验结果体现了很强的对Bell不等式的违背(轨道角动量这一自由度)。
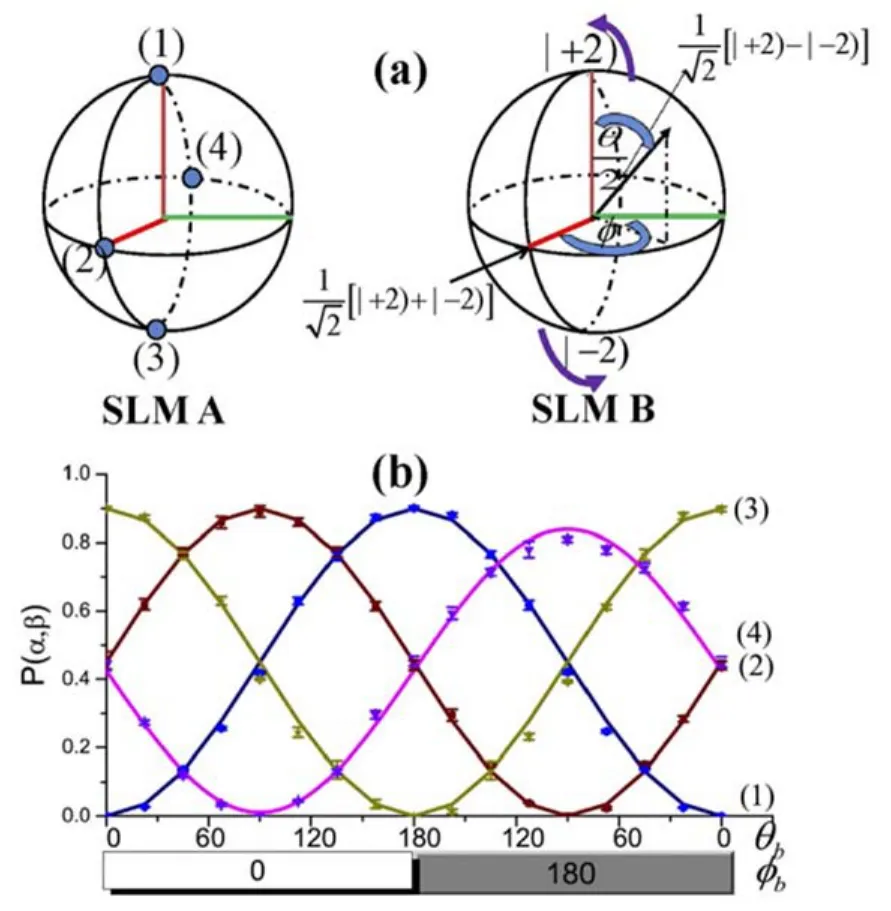
图13 (a)OAM态的Bloch球面,球面上的北极点和南极点分别对应OAM为+2和-2的状态;(b)经典OAM的关联曲线,不同曲线对应不同SLM A生成的投影基[(a)左侧],SLM B生成的投影基绕Bloch球两极进行变化[(a)右侧],图(b)中的点为实验数据,实线代表理论曲线[48]Fig.13 (a)Bloch sphere of OAM state.The north and south pole represent the OAM states of+2 and-2;(b)The classical correlation of OAM states.The different curves are measured by different projectors[shown in the left of(a)]generated by SLM A.The projectors generated by SLM B are set to be the states around the two poles of Block sphere[shown in the right of(a)].The points in(b)are experimental data,and the solid lines are the theoretical results[48]
分析Ea(r,t)和Eb(r,t)之间的偏振关联的方法与OAM关联类似,测量结果如图14所示。同样地,可以计算得到最大Bell值为|SPol|max=2.579±0.012,在θA=0,θ′A=π/4,θB=-π/8和θ′B=π/8处取得,这表明经典偏振自由度的关联也可以违背CHSH型的Bell不等式。上面两自由度的关联特性可以说明,偏振和OAM自由度展现的经典超关联特性[48]形式上与超纠缠的光子对拥有的量子关联关系类似。随后,基于这样的关联关系,他们进一步使用经典光模拟了量子超密编码方案。他们的方案设计如图15所示,主要分为三个部分:经典超关联源,由Bob执行信息编码的部分,以及由Alice执行信息解码的部分。类似于量子超密编码[50]中的幺正变换,对光场Ec(r,t)的两个自由度进行同样的整体操作。在如图15所示的编码阶段,Bob按照方案需要使用两个HWP,构造两条光路,达到每次操作仅能通过其中一条光束的效果,并选择性地在其中一条通道插入一个DP。最后再加上两个已选取合适角度的HWP,Bob就可以完成整个编码环节。实验结果表明,Bob的这些操作能够对应八种不同的信息,即实现了与量子超密编码对应的编码方案。
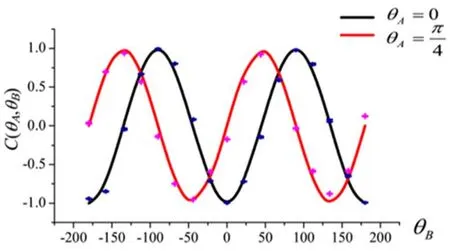
图14 当θA=0和θA=π/4时,偏振关联函数随偏振角θB的变化曲线,图中点为实验数据,实线代表理论曲线[48]Fig.14 The polarization function of θBwhen θA=0 and θA= π/4.The points are experimental data,and the solid lines are the theoretical results[48]
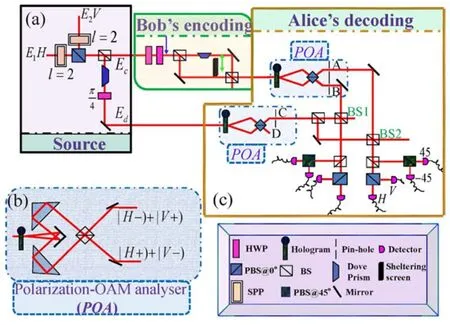
图15 基于经典关联的超密编码方案实验示意图。(a)经典关联源部分;(b)具体的偏振-OAM测量装置;(c)Bob的编码部分及Alice的解码部分[48]Fig.15 The super-dense code scheme based on classical light.(a)The classical correlation source;(b)The polarization-OAM analyzer;(c)The encoding and decoding performed by Bob and Alice,respectively[48]
在Bob完成编码后,输出的光将与没有经过任何操作的参考光共同发送给Alice。然后,Alice即可执行解码分析。通过记录8个端口的强度,Alice可以准确地识别Bob编码的信息。
依照超密编码的实验方案,Alice完成的解码结果由图16给出,实验数据经过总的探测强度进行了归一化。根据图16的结果,Alice由8个探测器的强度对Bob所编码的信息做出的判断是准确的,过程中的信息量为log28=3 bit。为了突出超纠缠的作用,Li等还考虑了仅使用Ec(r,t)或Ed(r,t)实现的编码过程。在该编码过程中,Bob同样对偏振和OAM执行整体的操作,此后,将光束传送到Alice处,由Alice进行解码。而此时,Alice得到的最大信息量为2 bit,此结果说明Li等[48]构造的基于经典超关联的编码方案是能够与量子超密编码方案对应的。
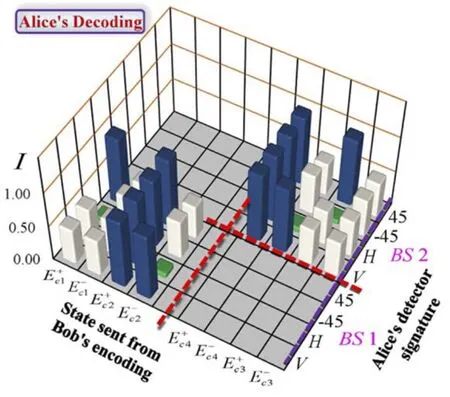
图16 基于超关联的超密编码与对应的解码实验结果[48]Fig.16 The decoding results of the super-dense encoding enabled by super correlation[48]
更重要的是,Li等的方案相较于量子超密编码方案具有许多优势。一方面,同样是使用8个正交的状态进行编码,由于在经典光系统中所编码的态能够被全部识别,所以能够获得3 bit的信道容量,而使用超纠缠光子对的信道容量只有log27≈2.8[50]。另一方面,由于经典光可以具有比较高的强度,此方案在现有光通信方案中也有机会实现。并且,此方案中的测量过程能够实时地识别收到的信息,并不需要进行长时间的符合测量。另外,需要强调的是,尽管此方案基于经典光关联,但不同于传统相干通信的信号解调[51-53]。比如,Han等[51]提出,可以将需要传递的信息加载在电磁信号的电场分量上,然后通过正交偏振的调制来提升信道容量。事实上,Li等提出的是一种新的复合编码方式,能够实现不同自由度的同时纠缠,具有更大的状态空间。
不仅如此,双光子的高维纠缠也已经被证明可以实现[54,55]。参考Ndagano等[34]使用经典光的不可分离态来表征大气湍流中量子信道的方案,实际上,空间可分离的经典关联光场也可以实现类似的表征方法,甚至可以实现数据的实时纠错。这个工作也是由Li等[56]完成的,他们在2018年实现了经典高维关联,实验方案如图17所示。如前所述,经典关联已经被证明在经典和量子系统中有很大的应用前景,例如提高测量精度、表征量子信道等。但之前的经典关联主要使用二维自由度,在实践中难以进一步扩展。于是,Li等基于干涉测量实现了一个经典的高维关联,它与量子高维纠缠有数学上的相似性,并显示出对高维Bell不等式的违背。此外,他们将Ndagano等[34]用经典光特征量子信道的思想扩展到了一般的高维状态,还从理论上证明了当单侧信道受到大气湍流扰动时,具有高维量子态的量子信道可以用他们提出的方案进行鲁棒的表征。并且,高维量子纠错也能被鲁棒地实时实现。Li等的结果不仅为经典关联的概念提供了新的物理见解,而且展现了其在高维量子信息处理中的潜在应用。
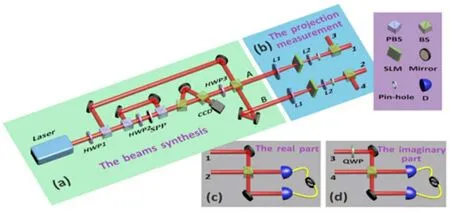
图17 经典高维关联实验装置示意图。(a)光源;(b)利用SLM、针孔、L1和L2耦合透镜组进行投影测量;(c),(d)分别为一阶关联函数实部和虚部的测量方案[56]Fig.17 Scheme of classical high dimensional correlation.(a)The light source;(b)Measurement setup composed of SLM,pinhole,lenses L1 and L2;(c),(d)Measurement scheme of the real and imaginary parts of the first-order correlations[56]
Li等的实验装置巧妙地实现了不同轨道角动量模式的完全非相干混合,最终得到的具有高维关联的光场A和B可以分别表示为
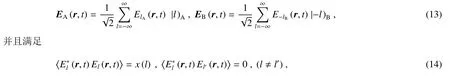
式中:〈···〉表示时间平均,x(l)代表了模式数l的函数。
为了描述光场EA(r,t)和EB(r,t)之间的关联关系,并进一步进行Bell测量,验证其是否违背Bell不等式关系,他们利用空间光调制器(SLM)和两个透镜组成的耦合透镜,在不同测量基上执行子空间的投影测量,最终得到关联概率函数的实验曲线,如图18所示。
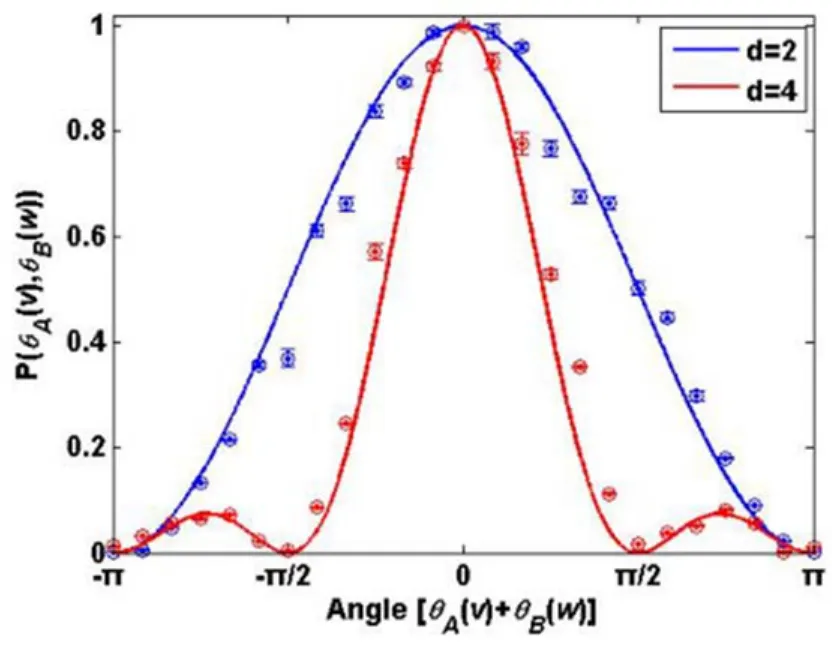
图18 关联概率作为角度θA(v)+θB(w)的函数,圆点为实验结果,实线为理论曲线[56]Fig.18 The correlation function of θA(v)+ θB(w).The round dots are the experimental results,and the solid lines are the theoretical results[56]
这里定义输出场的关联强度及关联概率为
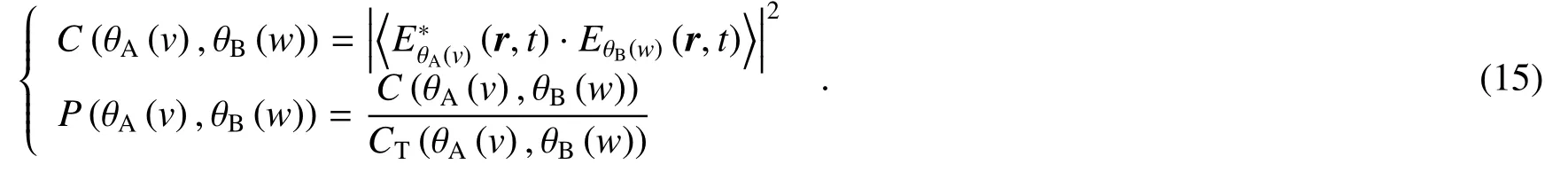
根据文献[54,55],量化这种关联关系的高维Bell不等式可以定义为
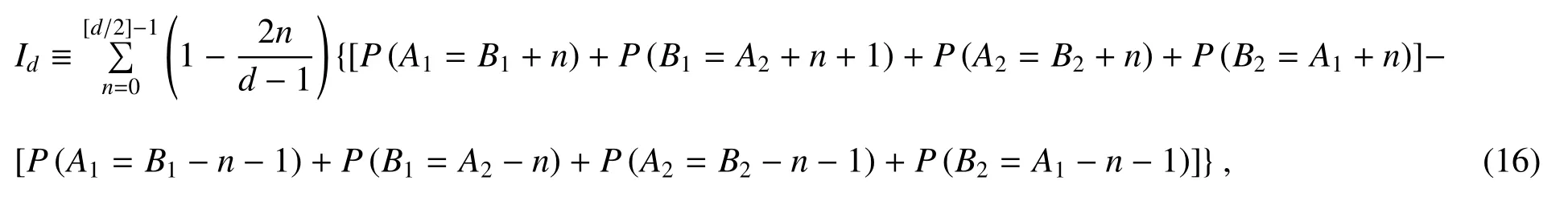
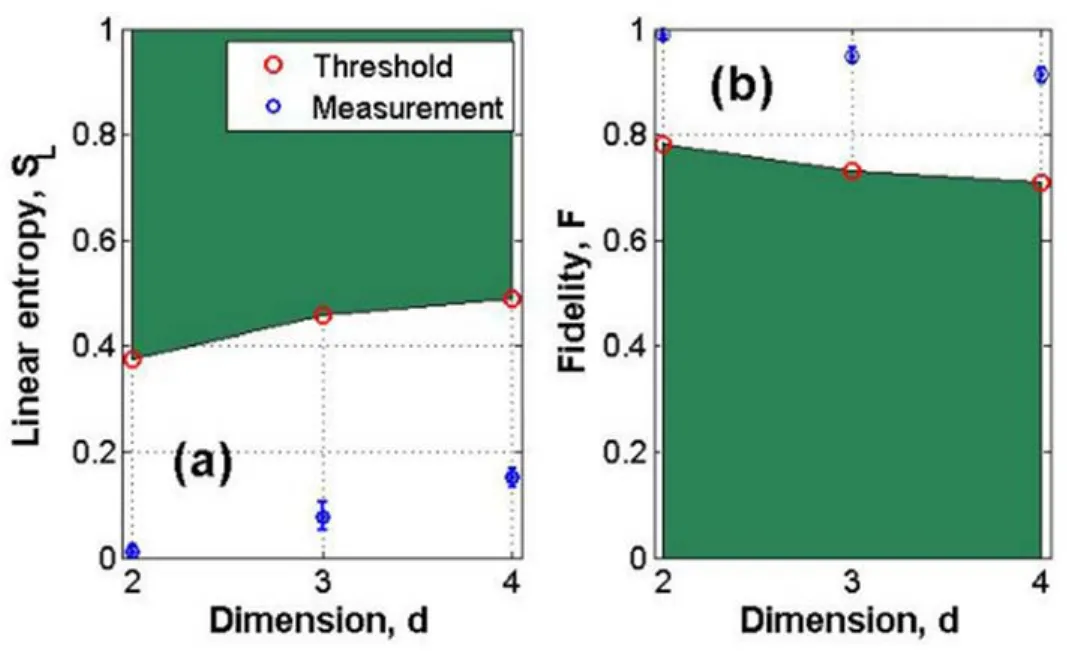
图19 (a)线性熵SL和(b)保真度F随维度d的变化关系。标有误差棒的蓝色圆点为实验测量结果,红色圆点代表了相应的阈值态,绿色阴影部分表示不能违背Bell-CGLMP不等式的状态范围[56]Fig.19 (a)The linear entropy SLand(b)the fidelity F as the functions of dimension d.The blue dots with error bars are the experimental results.The red dots are the threshold states.The states in green region do not violate the Bell-CGLMP inequality[56]
实际上,从上个世纪六十年代Bell不等式的提出到现在,人们对经典和量子边界的问题做了很多研究,除了根据局域隐变量理论得到的Bell不等式之外,还有Hardy定理、Steer关系、非关联隐变量理论、K-S理论[57]、单偶关系、互文性[58,59]和Leggett关系[60,61]等。这些关于经典和量子边界的理论能否借用上述经典关联光场的构造方法进行突破?实际上,关于经典和量子边界的问题人们一直在不懈地研究,下面列举一些结果供读者参考。如,Zhang等[62]使用经典光实现了Hardy的思想实验;Cabello等[63]对互文性的经典模拟进行了理论分析;Li等[64]用经典光完成了互文性的实验;Frustaglia等[65]证明了许多量子极限不是量子理论所独有的;Kurzy´nski等[66]描述了非局域性与互文性之间的单偶关系;Zhan等[67]在光子系统中用实验验证了单偶关系;Li等[68]在实验上使用经典光模拟了互文性和非局域性之间的单偶关系;Zhang等[69]实验上观察到了经典光系统中Leggett-Garg不等式的违背,等等。
至此,集中介绍了经典光学状态与量子纠缠之间的对应关系,简单回顾了基于轨道角动量光学自由度的局域不可分离态和空间可分离经典关联态的实现方法及若干应用。接下来,介绍利用轨道角动量状态来实现量子随机行走的方案,并介绍其中与状态拓扑性质相关的研究。
4 基于轨道角动量光束的随机行走研究
经典随机行走是用来描述经典物理中随机现象的一个理论模型。在经典物理中,花粉颗粒的布朗运动是展示经典随机现象的一个典型案例。尽管花粉颗粒受到经典随机力的作用,当观测花粉颗粒平均位置的分布时,其展现出的是近乎严格的经典高斯型分布,该分布可以用经典随机行走的理论来描述。经典随机行走不仅可以描述经典随机现象,还可以用于经典随机算法等方面的研究,因而受到研究者的广泛关注。近年来,人们发现当把量子相干等引入随机行走中,可以构造出所谓的量子随机行走,其在描述随机分布中会展示和经典物理完全不同的结果[70-75]。更进一步,研究者发现,由于量子随机行走结合了量子相干等性质,基于量子随机行走实现的量子算法可以在性能上大大地超过相应的经典算法[76-81]。不光基于量子随机行走的量子算法研究有了长足的进展,基于量子随机行走的拓扑物态研究也受到广泛的关注[82-88]。研究者已经在实验上构造出基于轨道角动量光的量子随机行走平台来研究拓扑现象。由于在自由空间的每个空间位置可以有多个不同模式的轨道角动量光相干叠加,因而可以在自由空间的一维位置空间里实现合成维度的二维量子随机行走[87]。
实现二维量子行走的实验装置如图20所示,包含3个模块:初态的制备[图20(a)],多步的二维量子行走[图20(b)]和结果测量[图20(c)]。波长为632.3 nm的He-Ne激光器输出的高斯光束携带的轨道角动量(OAM)为0。光束的光强可以通过一个半波片和偏振片调节,可以通过一个半波片和四分之一波片组合来制备其初始的任意偏振态。在该实验方案中,二维量子行走的“硬币”是编码在光束偏振状态上的。实验使用光的轨道角动量和空间位置两个自由度来映射出量子随机行走系统的二维位置空间。已有的研究表明:由于经典光学和量子力学中的相干过程相似,量子行走实验可以完全用经典光源代替单光子源[89-91]。因此,该方案使用经典的连续光源而不是单光子来执行实验。
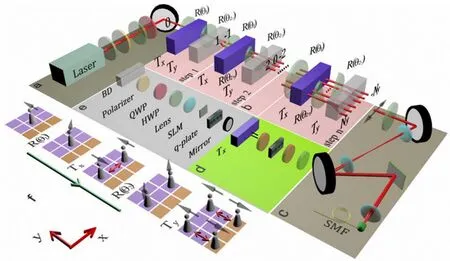
图20 二维量子行走的实验方案图。(a)初态制备;(b)多步的二维量子行走;(c)探测装置;(d)Tx具体包含的器件;(e)光学器件列表;(f)二维量子行走第一步的具体演化过程[87]Fig.20 The two-dimentional quantum walk experiments.(a)Preparation of the initial state;(b)The multiple steps of two-dimentional quantum walk;(c)The detection devices;(d)The devices employed in operation Tx;(e)Illustration of the optical elements;(f)Evolution of the state in the first step[87]
二维量子行走的一步演化算符可以描述为

可以通过一个半波片作用在光束的偏振态上实现硬币空间的旋转算符实现装置为图20(b)中的R(θ1)和R(θ2)标识的元件。σy和σz是泡利矩阵,参数θ1(2)是半波片的旋转角度。公式
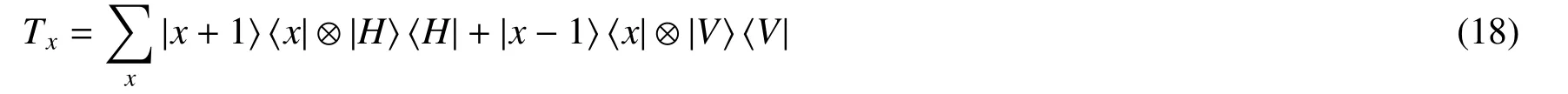
代表行走者沿着x方向的条件平移算符。使用光束不同的OAM的值代表行者走在x方向上不同的位置,|H〉和|V〉代表光束的水平偏振和竖直偏振态。条件平移Tx根据光束偏振态对OAM态执行不同的平移操作。具体实现条件平移Tx的元器件见图20(d)。通过双折射晶体(BD)实现条件平移
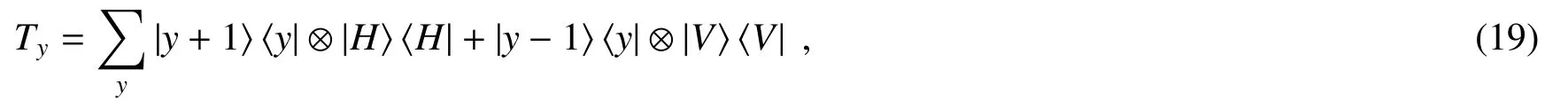
从BD出射的不同空间位置代表行走者沿y方向的不同位置[84,92-94]。
接下来具体介绍如何在实验上实现条件平移算符Tx和Ty。在本研究组的实验中,条件平移算符Tx是通过两个半波片和一个拓扑电荷为0.5的q-plate构成的三明治结构实现的,紧跟着的一个半波片(@0)作为相位补偿。q-plate的功能一般来说可以描述为
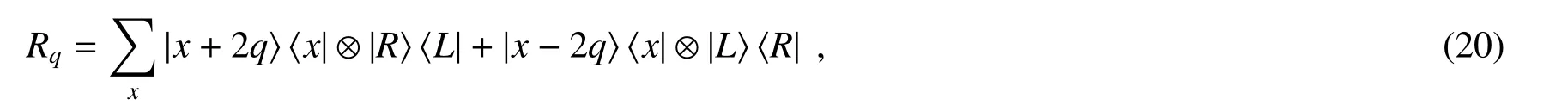
式中|L〉和|R〉分别代表左旋和右旋圆偏振态。在两个正交的水平偏振态和竖直偏振态下,圆偏振态定义为:其中x的值表示光束OAM的取值,q-plate可以根据光束的偏振态|L〉(|R〉)对光束OAM的状态平移2q(-2q)。实验中使用的q-plate的拓扑电荷为q=0.5。四分之一波片的琼斯矩阵是
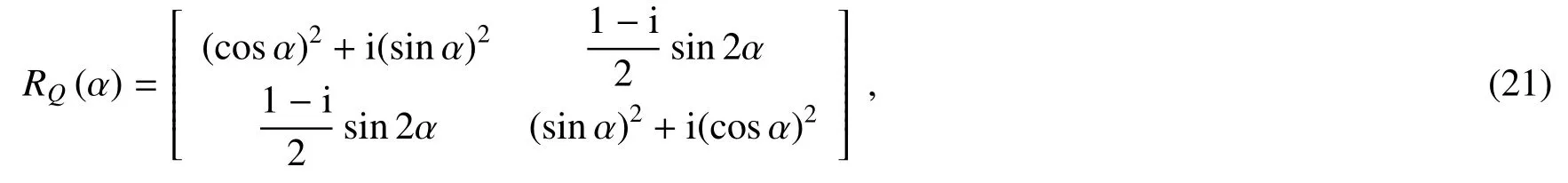
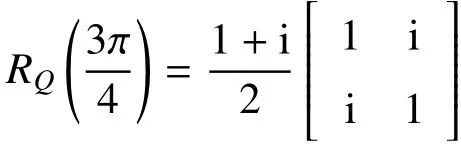

旋转角度β代表QWP的光轴相对于水平方向旋转β。如图20(d)所示,两个半波片、一个拓扑电荷为0.5的q-plate和一个半波片组合成了沿x方向的条件平移算符Tx,可表示为
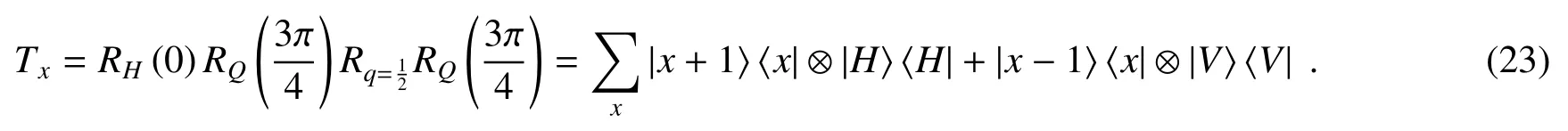
实验中,每个q-plate的透过率高达92%。在一步的演化过程中,一个光斑通过BD后,根据不同的偏振态分成固定间隔为3 mm的两个光斑。为了匹配经过多个BD产生的多个光斑,定制了包含多个图案的q-plate,每一个图案的通光孔径为2.5 mm×2.5 mm,并且相邻图案之间的间距为3 mm。条件平移算符Ty是通过BD实现的,由于双折射效应,一个光斑通过BD后,根据不同的偏振态分成固定间隔为3 mm的两个光斑。通过角度切割BD,可以实现水平偏振的光束传输方向不变直接透射,而竖直偏振的光束经历了一个3 mm的空间平移至相邻的格点。这样便实现了条件平移算符Ty的功能。从BD出射的多个光斑的空间位置代表二维量子行走沿y方向的格点。随着步骤的增加,从BD出射的光斑数目也在增加。在本实验中,最大的一块BD的尺寸是20 mm×7 mm。
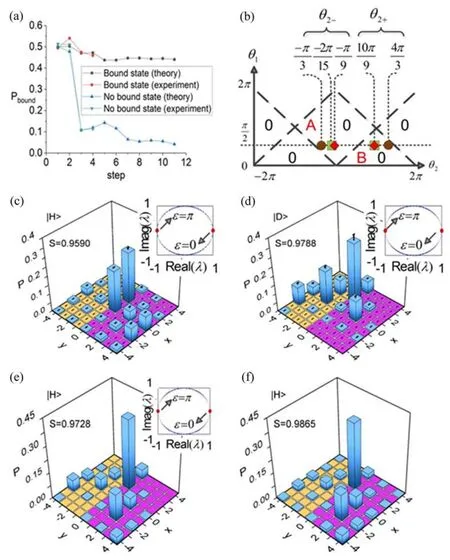
当在实验上搭建了结合光的轨道角动量和空间位置的二维量子随机行走平台后,就可以研究二维量子随机行走的拓扑性质了,如图21所示。为了观测拓扑态,需要构造不均匀的量子随机行走。这是通过半波片对位置区域0≤y 图21 (a)~(c)实验观测束缚态。(a)二维量子行走的相图;(b),(c)分别代表在绿色方块参数下演化算符的本征值λ=e-iε和演化四步的概率分布[图(b)中红色点代表束缚态,图(c)在界面处有局域化的概率分布];(d)~(f)实验上没有观测到束缚态。(d)二维量子行走的相图;(e),(f)分别代表在红色三角参数下演化算符的本征值λ=e-iε图和二维量子行走演化四步的概率分布图,误差棒代表概率的标准差[87]Fig.21 (a)~(c)Experimental observation of the bond states.(a)The phase diagram of the two-dimensional quantum walk,(b)the eigenvalue λ =e-iε of the evolution,and(c)the probability distribution after four steps,under the parameters of the green squares shown in(a).(c)is the localization probability of the interface.(d)~(f)The results without bond states.(d)is also the phase diagram of the two-dimensional quantum walk.(e)and(f)are similar to(b)and(c),while under the parameters of the red triangles shown in(d).The error bar gives the standard deviation of the probability[87] 从图21(c)可以明显看出有很强的局域化几率出现在y=0的界面上,这也是存在边界态的一种标志。硬币算符的旋转角度(θ1,θ2,-)和(θ1,θ2,+)分别标记在图21(a)中区域A和B的绿色方块上。当旋转角度从(θ1,θ2,-)连续地变换到(θ1,θ2,+)时,二维量子行走需要穿越虚线标记的无带隙区域。图21(b)给出了演化算符U的本征值λ=e-iε。发现能量为ε=0和ε=π的束缚态出现在两个区域A和B的陈数为0的边界上。在这种情况下,发现出现的束缚态不能用陈数来刻画,并且体边界定理失效了。 作为对比,选择旋转角度(θ1,θ2,-)和(θ1,θ2,+)分别标记在图21(d)中同一区域A中。接下来研究在这组参数下演化算符U的拓扑特性。发现当硬币算符的旋转角度从(θ1,θ2,-)连续地变换到(θ1,θ2,+)时,二维量子行走的有效哈密顿量不会经过带隙闭合的过程。对应的演化算符U的本征值λ=e-iε显示在图21(e)中,此时没有孤立的本征值出现即束缚态存在。与图21(b)完全不同的是,当旋转角度取同一区域A中参数时,几率分布在界面y=0处迅速下降[如图21(f)]。结果表明,在后一种情况下,界面处没有束缚态。 这样的拓扑边界态是具有鲁棒性的。在实验中,本研究组证明了束缚态对微小的静态扰动和无序的鲁棒性。 研究静态扰动对图21(c)界面态的影响。静态扰动可以通过两种方式引入:微小改变旋转角度的静态扰动和初始偏振态的静态扰动。图22(b)中的棕色圆圈表示对图21(c)中的角度引入微小的扰动,相应角度下演化四步的概率分布显示在图22(c)中。在图22(c)的插图中,可以看出微小扰动后的角度下,红色实心圆点的束缚态仍然存在。发现当旋转的角度没有越过无带隙的区域,在边界处总是出现较高的局域化概率。图22(d)是将图21(c)初始偏振从|H〉变化为|D〉时演化四步的概率分布,发现在边界上界面态仍然存在。因此,图21(c)所示界面态对微小的静态扰动是具有鲁棒性的。 图22 (a)二维量子行走在界面处的局域化几率Pbound随步骤的变化图;(b)二维量子行走的相图,在两个不同的区域A和B中棕色圆圈、绿色方块和红色菱形选取的角度分别对应于图(c)、(d)和(e)中所使用的角度;(c),(d)束缚态对于微小的静态扰动是鲁棒性的;(e),(f)束缚态对无序的鲁棒性证明[87]Fig.22 (a)Variation of localization probability Pboundof the interface of two-dimensional quantum walk with the step number;(b)Phase diagram of the two-dimensional quantum walk.In different regions A and B,the angle parameters of the brown circles,green square and the red rhombuses correspond to those used in(c),(d)and(e)respectively;(c),(d)indicate the robustness of the bond states under small perturbations;(e),(f)prove that the bond states are robust against the disorders[87] 当旋转角度引入无序后,也在实验上证明了拓扑束缚态仍然存在。实验上,无序是通过在旋转角度θ2±上加上一个在区间[-2π/9,2π/9]上满足均匀分布的随机扰动δθ。随机选取十组角度,对得到的十组概率分布取平均值,相应的概率分布显示在图22(f)中。图22(e)给出了旋转角度没有加入无序时演化的结果。通过对比,可以看出二维量子行走在有无序的参数条件下的概率分布[图22(f)]高度相似于没有加入无序的参数下[图22(e)]的概率分布。因此,这些结果证明了界面态对无序的鲁棒性。 通常情况下,人们认为拓扑保护的束缚态会出现在两个具有不同拓扑相的区域的界面处,而本研究组的研究结果表明,在两个拓扑相相同(陈数为0)的区域界面处,也存在拓扑保护的束缚态,这种现象不符合以往在静态系统中对于陈数的理解,而是周期性驱动的离散随机行走中特有的现象。在二维量子行走系统中,本研究组从实验上证明了反常的拓扑保护的束缚态的存在。该研究结果丰富了人们对拓扑相的理解,并为研究高维量子随机行走的拓扑现象提供了一种新途径。 对近年来有关轨道角动量光束中经典光关联及其应用的研究做了介绍。从信息科学的角度而言,光学的轨道角动量自由度提供了一种重要的编码方式。轨道角动量态自身构成了一个高维空间,因此一个包含多组轨道角动量态的光束自身就可以编码多个bit的信息。这种高维编码尽管实际上与二进制编码等效,但有机会实现单个信道容量的提升,以及信息操作方面的化简。此处介绍的许多工作都展示了其在该方面的性质。从探测技术的角度而言,轨道角动量态在垂直于光场传播方向上可以提供相位梯度,这使得利用轨道角动量光束照射行动物体之后得到的回波,可以获取物体的横向运动信息。这种性质对远程探测技术十分重要,尤其是在推广到雷达技术时有着很大的应用潜力。本文主要着眼于物理问题的研究和总结,因此涉及这些方面的介绍相对较少。另外,与经典光关联相结合,轨道角动量状态有了更大的发挥空间。一些基于量子特性的光通信方案可以通过含有轨道角动量自由度的经典关联态(包括局域不可分离态)来对应实现。这样的实现方法相较于传统通信方案是一种改进,并且不需要引入类似量子光源的相对苛刻的装置。在探测技术上,量子度量学理论提供了一种在精度上优于传统探测的方案。相信通过结合轨道角动量状态与经典关联,量子度量学中的基于量子光的探测方案也可以通过经典系统实现。实际上,这些相关的研究也暗示了可能并非所有的“量子优势”都是量子系统所独有的特点。在特殊经典系统中构造出类似优势,无论对量子理论还是经典理论而言都是一种发展。 总之,目前关于光学轨道角动量态调控的研究实际上还处于初步阶段,如何构造出高效的角动量调控元件依然是一个重要的研究课题。这样的元件势必会使轨道角动量态在光通信或者光信息处理过程中更好地发挥上述优势。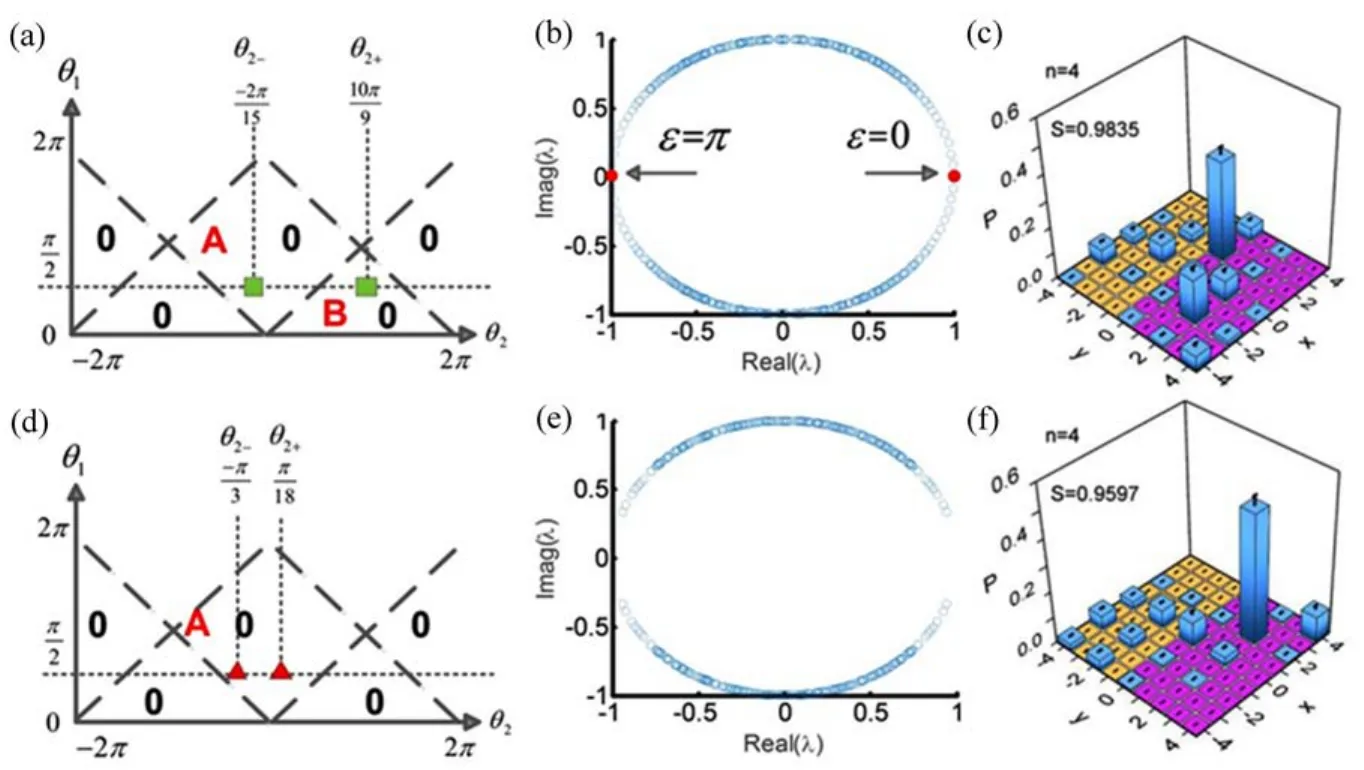
5 总结
