基于SPH法微切削单晶锗动态过程模拟研究
2022-04-12杨晓京杨红秀
杨晓京,杨红秀
(昆明理工大学 机电工程学院,云南 昆明 650500)
单晶锗属于脆性材料,具有面心立方晶体结构,含有(111)、(110)、(100)共3个晶面。其中,每个晶面都存在着晶向各向异性的特点。在加工时,因其(111)晶面的加工与使用性能优于其他两个晶面,所以常将(111)晶面应用于制造热像仪、夜视仪系统中的窗口、透镜等关键器件[1~5]。目前,单晶锗的加工方法主要为单点金刚石车削、飞切、磨削和抛光。飞切加工可有效避免晶向各向异性对加工表面质量的影响,得到光滑的加工表面[6~8]。因此,本文采用了一种新兴的无网格仿方法,即光滑粒子流体动力学(Smoothing Particle Hydrodynamics,SPH)[9]来对飞切加工过程进行模拟。该方法不仅克服了有限元法难以处理的切削区域大变形及切屑分离等问题,还不受加工尺度和计算时间的限制,可较好地模拟脆性材料的切屑分离过程[10]。文献[11~13]利用SPH法针对脆性材料进行了数值模拟。但是目前,关于SPH方法对单晶锗去除机理的研究较少。因此,本文基于动态分析软件LS-DYNA及后处理软件LS-PREPOST,用 SPH方法对单晶锗飞切过程进行模拟,研究单晶锗塑性去除时,切削深度、切削速度与切削力和切屑形成的关系,为单晶锗塑性域材料去除提供一定参考。
1 仿真模型的建立
1.1 SPH数值建模
本文采用SPH数值建模,将单晶锗飞切区域设计成40 μm×30 μm×5 μm并用SPH 粒子填充。单晶锗(111)晶面微切削仿真图如图1所示,刀具切削参数详见表1。

图1 单晶锗(111)晶面微切削仿真Figure 1. Simulation of micro-cutting on single crystal germanium (111)

表1 刀具切削参数Table 1. Tool cutting parameters
1.2 材料建模
材料模型及参数在数值仿真中起着很关键的作用。本文所使用的刀具材料为单点金刚石。由于本文不研究刀具的受力及变形,因此将刀具看作刚体。以单晶锗(111)晶面作为切削仿真对象,并选用J-C本构模型,其具体形式见文献[14]。仿真中所需材料参数如表2和表3[15]所示。

表2 单晶锗(111)晶面物理参数Table 2. Physical parameters of single crystal germanium (111)

表3 J-C本构参数Table 3. J-C constitutive parameters
1.3 定义接触及边界条件
本文将刀具几何表面作为主接触面,工件整体SPH节点域为从面,接触类型为罚摩擦,摩擦系数为0.2[16],采用AUTOMATIC_NODES_TO_SURFACE自动点面接触的接触方式。在设置工件的边界条件时,针对SPH模型,在软件LS-PREPOST中选用了专用边界SPC(对称平面约束),固定工件底面、两侧面,对刀具施加沿z轴正方向的切削速度,限制其余所有自由度以防止其在切削过程中发生偏移。
2 计算结果与讨论
将切削力分为3个分力:(1)与z轴平行的切向力;(2)与y轴平行的法向力;(3)与x轴平行的轴向力。在该仿真模型中,轴向力较小,因此本文中忽略轴向力,仅考虑切向力及法向力所受影响。
2.1 切削深度对切削力的影响
为了研究单晶锗在加工过程中切削力受切削深度的影响,本文选取的切削速度为4 μm·μs-1,切削深度分别为0.5 μm、1 μm、2 μm和5 μm,其关系变化曲线如图2所示。
图2(a)为切向力变化曲线,图2(b)为法向力变化曲线。由图2可知,工件所受的切向力及法向力都出现逐渐增大,随后略微减小,最后平稳波动的趋势。当切削深度为0.5 μm时,切向力和法向力的稳定波动值分别为0.01 mN和0.02 mN。当切削深度为1 μm时,切向力和法向力的稳定波动值都为0.04 mN。当切削深度为2 μm时,切向力和法向力的稳定波动值分别为0.08 mN和0.06 mN。当切削深度为5 μm时,切向力和法向力的稳定波动值分别为0.24 mN和0.11 mN。
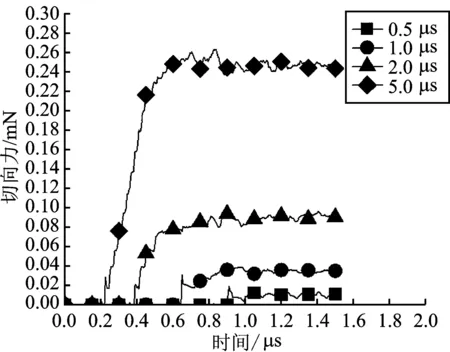
(a)
(a)
当切削深度为0.5 μm、1 μm、2 μm时,切削深度小于刀尖圆弧半径,工件表面主要受刀尖的圆弧半径对其正压力的作用,故而切向力与法向力在切削过程中相差不大。当切削深度增加到5 μm时,在切削过程中切向力主要受前刀面的影响,法向力主要受后刀面的影响,前刀面对工件的影响效果比后刀面大,因此切向力的稳定波动值大于法向力稳定波动值。
2.2 切削速度对切削力的影响
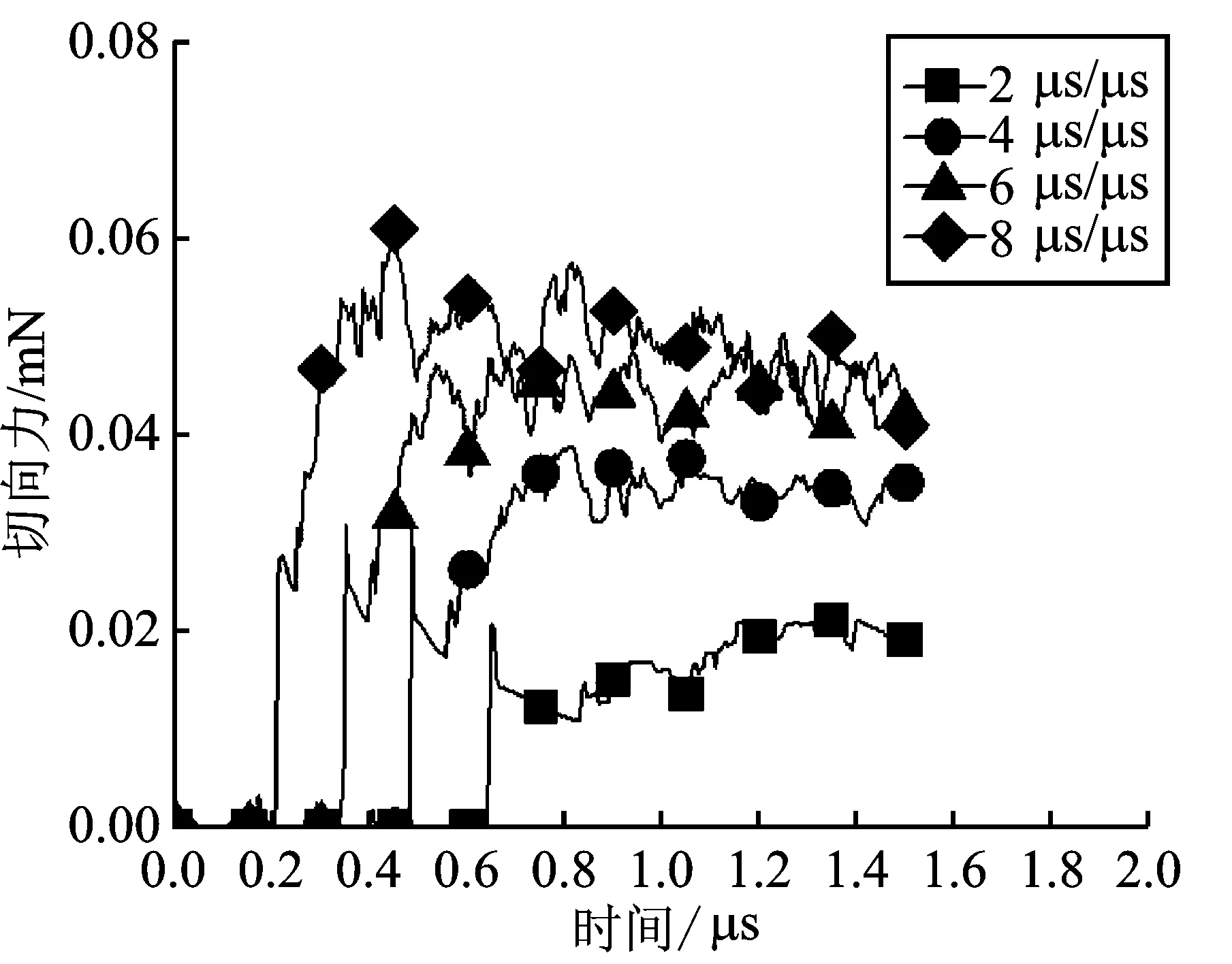
为了研究切削速度对单晶锗工件表面切削力的影响,取切削深度为1 μm,切削速度分别为2 μm·μs-1、4 μm·μs-1、6 μm·μs-1、8 μm·μs-1,其关系变化曲线如图3所示。
图3(a)为切向力变化曲线,图3(b)为法向力变化曲线。由图3可知切削速度为2 μm·μs-1时,切向力及法向力的稳定波动值都为0.02 mN,且波动幅度较小。切削速度为4 μm·μs-1时,切向力及法向力的稳定波动值都为0.03 mN,波动幅度较小。切削速度为6 μm·μs-1时,切向力及法向力的稳定波动值分别为0.04 mN和0.05 mN,波动幅度较小。切削速度为8 μm·μs-1时,切向力及法向力的稳定波动值分别为0.05 mN和0.06 mN,波动幅度较大。以上结果表明,切削速度对切向力及法向力数值的影响不大,但切削速度越大,切向力及法向力的波动幅度越大,切削越不平稳。

(a)
2.3 切削深度对切屑形成的影响
切屑的形成受多种因素的影响。为了研究单晶锗形成切屑受切削深度的影响,本文在4 μm·μs-1切削速度下,改变刀具的切削深度来进行分析。如图4所示为1.5 μs时刻的仿真结果放大图。
如图4(a)所示,当切削深度为0.5 μm时,工件材料只有滑擦,没有切屑产生。如图4(b)所示,当切削深度为1 μm时,滑擦作用增强,进入犁耕阶段刀具两侧隆起会产生毛刺,且表面出现微小切屑。图4(c)表明,当切削深度为2 μm时,切屑的产生更加明显。在设定的切削参数下,单晶锗(111)晶面产生切屑的临界切削深度在0.5~1 μm范围内。如图4(d)所示,在塑性去除下,切削深度越深,越容易形成带状切屑,两侧隆起及产生毛刺也越严重。

(a)
2.4 切削速度对切屑形成的影响
为了研究单晶锗形成切屑受切削速度的影响,在切削深度为1 μm情况下,通过改变刀具的切削速度来进行分析。如图5所示为1.5 μs时刻的仿真结果放大图。
当切削速度为2 μm·μs-1时,单晶锗(111)晶面只受滑擦,没有切屑产生。当切削速度为4 μm·μs-1时,滑擦作用增强,进入犁耕阶段刀具两侧隆起会产生毛刺,并伴有微小切屑出现。当切削速度为6 μm·μs-1时,可以明显观察到切屑的出现,说明在设定的切削参数下,单晶锗(111)晶面产生切屑的临界切削速度在2~4 μm·μs-1之间。在塑性去除下,切削深度越深,越容易形成带状切屑,两侧隆起及产生毛刺也越严重。
3 结束语
由于实验条件和研究成本限制,本文未进行试验验证,但现阶段已有研究人员对单晶锗进行了一系列微切削试验,文献[17~18]可得到相似变化规律,因此可以间接验证SPH法仿真的可行性。将SPH方法应用于模拟单晶锗(111)晶面微切削飞切过程,得出以下结论:(1)用SPH无网格法建立了单晶锗(111)晶面三维切削模型,模拟微切削单晶锗形成切屑的过程,规避了有限元法难以处理的切削区域大变形、切屑分离等问题;(2)在切削速度为4 μm·μs-1,切削深度为0.5 μm、1 μm、2 μm、5 μm情况下,切向力及法向力都出现逐渐增大随后略微减最后趋于平稳波动的趋势,且切削深度越大,切削力稳定波动值越大;(3)在切削深度为1 μm时,单晶锗切削速度选取2 μm·μs-1、4 μm·μs-1、6 μm·μs-1、8 μm·μs-1时,切削速度对切向力及法向力值的影响不大,且切削速度越大,切向力及法向力的波动幅度越大,切削越不平稳;(4)在切削速度为4 μm·μs-1,切削深度为0.5 μm、1 μm、2 μm、5 μm情况下,单晶锗(111)晶面切屑形成的临界深度为0.5~1 μm之间。在切削深度为1 μm时,单晶锗切削速度为2 μm·μs-1、4 μm·μs-1、6 μm·μs-1、8 μm·μs-1时,切屑形成的临界速度为2~4 μm·μs-1之间;(5)在单晶锗微切削仿真分析中,可以继续研究单晶锗微切削脆塑转变临界深度以及切削温度对加工表面质量的影响。
