基于突触可塑性的SNN随钻陀螺仪漂移处理
2022-04-12杨金显韩玉鑫刘鹏威
杨金显,韩玉鑫,刘鹏威
(河南理工大学 电气工程与自动化学院,河南 焦作 454000)
微电子机械系统(Micro Electro Mechanical Systems,MEMS)陀螺仪的惯性测量单元具有低成本、低功耗、小尺寸等优点,在捷联惯性导航系统领域[1-2]有着广泛的应用。然而,在随钻测量的背景下,由于地下环境复杂,在实际的钻进过程中存在由多种噪声源及温度变化所导致的测量数据漂移。温度引起的弹性变形等不确定干扰因素也会导致MEMS陀螺仪从数据采集到姿态解算的过程中产生较大的非线性误差[3-4]。MEMS陀螺仪的误差主要来源于数据漂移,大致可以分为随机漂移和确定性漂移。随着制造工艺的提高,零偏、非正交误差、刻度误差引起的确定性漂移得到了改善。随机漂移主要使量化噪声、速率斜坡、角速率等产生偏差,随着时间的累积,姿态角信息的误差会不断加大[5]。因此,处理随机漂移对MEMS陀螺仪精度的影响有着重要的研究意义。
目前,MEMS陀螺仪的处理方法大致可以分为基于模型的误差补偿和基于数据的特征提取。通过对陀螺仪工作环境下的误差分析,可以构建多种数学模型来逼近陀螺仪的工作状态[6-8]。此外,通过比较模型预测和状态监测的实时输出,可较为有效地处理陀螺仪随机漂移问题。但是在复杂环境下影响陀螺仪测量精度的因素较多,各项间的关系较复杂,通过构建一个精确的模型难以模拟陀螺仪的存在误差。数据驱动方法通过训练学习提取陀螺仪的特征信息,消除了噪声对陀螺仪的影响。文献[9]提出了一种基于自适应模糊C-均值聚类(Fuzzy C-Means Algorithm,AFCM)算法的T-S模糊方法,利用改进的AFCM优化减法聚类来确定聚类数目上限及聚类中心,从而有效确定规则数和聚类中心,并通过最小二乘估计模糊模型达到陀螺仪降噪的目的。文献[10]在小波阈值去噪的基础上,分离陀螺仪输出信号的白噪声和漂移误差,并通过BP(Back Propagation)神经网络预测漂移误差,以阈值降噪和BP神经网络结合的方法对陀螺仪漂移误差进行补偿。生物神经科学的研究表明,人工神经网络基于脉冲信号处理信息,其神经元信息处理机制接近生物神经元[11],可有效处理陀螺仪的非线性误差。传统神经网络的神经元在信号输入时均被迭代激活,脉冲神经网络(Spiking Neuron Networks,SNN)在处理陀螺仪信息的过程中,不断积累膜电位,仅在突触前膜电位达到预定值时,突触后膜电位激活,降低了该网络的整体功耗。突触可塑性与神经系统的自适应密切相关,是神经元间信息传递的基础[12-13]。文献[14]发现STDP(Spike Timing Dependent Plasticity)机制有助于神经网络中长期记忆模型的稳定存储。文献[15]发现,在抑制性STDP的控制下,激发性突触可达到稳定状态,保证输出层神经元处于动态平衡状态。文献[16]利用自适应脉冲神经网络的突触可塑性,研究了在复杂的电磁环境下该网络对噪声的抗干扰特性。
通过以上分析,本文提出了基于突触可塑性的脉冲神经网络来处理振动环境下陀螺仪的噪声干扰。本文提出的方法根据突触可塑性的特点,调节激发性和抑制性突触电导的大小,提高了网络的整体性能。本文通过分析网络输出神经元的点火率以及神经元膜电位间的相关性,验证了该方法的性能。
1 脉冲神经网络模型
SNN网络同传统人工神经网络(速率编码)的主要区别在于时间序列的编码方式。SNN网络计算速度更快,处理信息实时性更强。脉冲触发的时间序列表示输入的MEMS陀螺仪信息。不同神经元的点火时间编码不同的陀螺仪数据。本文采用群体编码的方式处理陀螺仪的输入数据,将输入的陀螺仪信息分布到多个神经元的脉冲时间上。利用群体编码的方式可有效地将陀螺仪的信息特征转化为脉冲触发的时间序列。群体编码通过利用输入陀螺仪数据的不同均值和相同方差的高斯模型编码数据。具体如式(1)~式(3)所示
(1)
(2)
(3)
式中,A为最大的脉冲时间;m为高斯接收域的个数;γ为控制参数。
1.1 Izhikevich神经元模型
Izhikevich神经元模型的本质为二阶微分方程,并结合了IF(Integral-and-Fire)神经元模型和H-H(Hodgkin-Huxley)神经元模型的优点。由于该模型与实际神经元的放电特性相似,适用于大规模神经网络的计算,因此可将Izhikevich神经元模型作为网络的节点用于处理陀螺仪受到的随机噪声干扰。在振动噪声干扰下的Izhikevich神经元模型方程为
(4)
式中,v为神经元膜电位;u为膜恢复变量;当K+离子电流激活,Na+离子电流失活时,膜电位v提供负反馈;I表示外部输入电流Iin和突触电流Iest之和;a为变量u恢复的时间尺度;b表示恢复变量u对膜电位v阈值下波动的灵敏度;c为膜电位v的峰后重置值;d表示恢复变量u的峰后重置值。Izhikevich神经元模型可以通过调整无量纲参数a、b、c、d来模拟多种点火模式;ξ(t)代表均值为零的振动高斯白噪声。
〈ξi(t),ξj(t′)〉=Dδijδ(t-t′)
(5)
式中,ξi(t)表示神经元i接收到噪声干扰;ξj(t)表示神经元j接收到噪声干扰;D为陀螺仪工作过程中的振动频率。本文采用RS (Regular Spiking)作为兴奋性神经元的激活模式,并采用LTS (Low-Threshold Spiking)抑制神经元的激活模式。RS和LTS的点火方式的参数如表1所示。RS点火方式和LTS点火方式分别如图1和图2所示。

表1 RS与LTS点火模式的参数Table 1. RS and LTS ignition mode parameters

图1 RS点火模式Figure 1. RS ignition mode
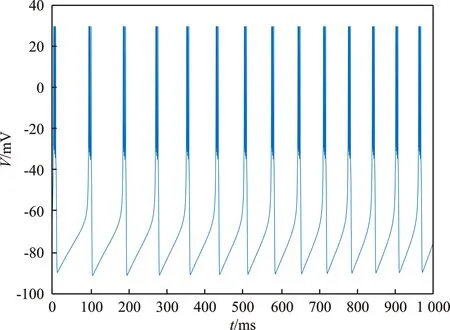
图2 LTS点火模式Figure 2. LTS ignition mode
1.2 突触可塑性
突触可塑性是指突触的形态和功能的变化,是神经元之间信息传递的基础。在突触模型中,突触后输入电流与输入电压之间的关系近似线性可以表示为
Isyn=g(Vsyn-V)
(6)

(1)突触前激发神经元j放电时,激发性突触电导的调节规则为
(7)
(8)
(9)

(2)突触前抑制神经元j放电时,抑制突触电导的调控规则为
(10)

激发性突触传导的调控规则为
(11)
抑制性突触传导的调控规则为
(12)
式中,τE和τI分别表示激发性突触的电导性和抑制性突触电导的衰减常数;gmin=0和gmax=0.015分别是突触电导权重的最小值及最大值;τ+和τ-分别表示突触增强和突触衰减,其中衰减常数τ+=τ-=20 ms。
1.3 SNN网络模型的构建
SNN网络中每层神经元的信息传输[18-19]是通过调节兴奋性突触电导和抑制性突触电导的参数来实现的。基于此,本文构建了10层前馈SNN网络,拓扑结构如图3所示。
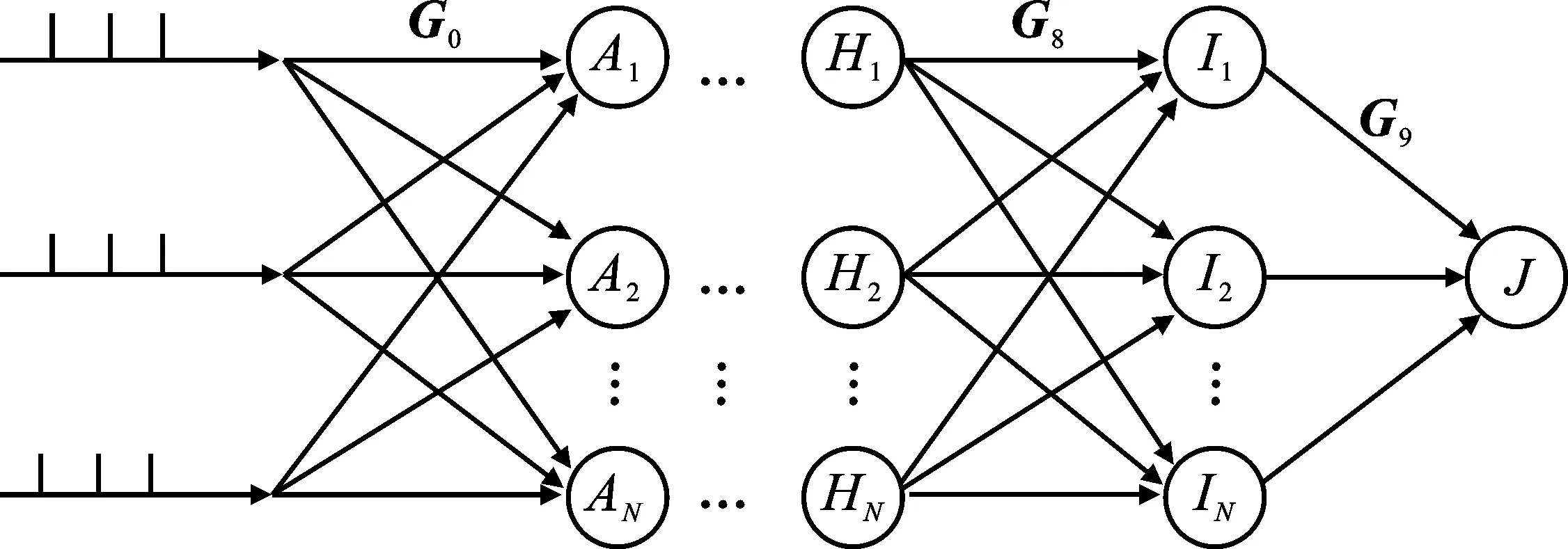
图3 网络拓扑结构Figure 3. Network topology
在图3中,输入层是以发射频率为10 Hz的脉冲序列,该网络有一个输出层,G0到G9是每层神经元的权重矩阵。初始权重在区间[gmin,gmax]中选择,根据生物特性,网络中的兴奋性神经元与抑制性神经元的的突触权重比为4∶1。
2 振动噪声下陀螺仪的干扰抑制能力分析
MEMS传感器的误差来源包括随机噪声、偏差、比例因子、交叉耦合误差和轴向对准误差等。白噪声和动静态偏差是MEMS传感器的主要误差。强烈的振动是产生高斯白噪声的主要原因。本文通过将不同振动频率的高斯白噪声添加到网络的所有神经元中研究脉冲神经网络的干扰抑制能力。输出层中神经元的膜电位与点火率之间的相关性是评估干扰抑制能力的重要指标。
2.1 不同振动频率下点火率
脉冲间隔ISI值为一个神经元的两个相邻放电时刻之间的差值。单个神经元的放电速率可以通过1 000/ISI的平均值得到。层放电速率是各层中神经元放电速率的平均值。本文通过振动噪声干扰前后输出层神经元放电速率的相对变化来评价SNN网络的干扰抑制能力。噪声扰动后点火率的相对变化越小,SNN的抑制噪声能力越好。
为了验证振动噪声对SNN点火率的影响以及噪声扰动下输出层神经元点火率的变化,本文设计了振动台实验,如图4所示。将MIMU模块水平固定在振动台上,设置0~50 Hz,步进为10 Hz的振动频率,网络中所有神经元均受到噪声的干扰。

图4 振动台装置Figure 4. Vibrating table device
实验结果表明,网络的点火率范围在0~50 Hz。图5为不同振动噪声频率下的输出点火率,当振动频率低于6 Hz时,输出点火率随噪声增强而增加。当振动频率在6~35 Hz时,输出点火率上下波动较大。当振动频率在35~50 Hz时,输出点火率趋于平稳状态。图6为不同振动频率下输出点火率的相对变化,当振动噪声频率在0~15 Hz范围时,相对变化输出点火率的变化范围为0.03%~4.51%。当振动噪声频率在15~50 Hz范围时,相对变化输出点火率的变化在2.43%~5.01%的范围内。

图5 不同振动频率下输出点火率Figure 5. Output ignition rates under different vibration frequencies

图6 不同振动频率下输出点火率的相对变化Figure 6. The relative changes of output ignition rates under different vibration frequencies
2.2 神经元膜电位间的相关性
为进一步验证本文所提方法的有效性,通过噪声扰动前后膜电位的相关系数来评估振动噪声对SNN的影响和干扰抑制能力,该系数可表示为
(13)
式中,ρij(τ)表示扰动神经元膜电位xi(t)与扰动后神经元膜电位xj(t)的相关系数;[t1,t2]为模拟持续时间;采用相关系数ρij(τ)评估扰动前后神经元膜电位之间相似程度,其值越大,表明脉冲神经网络的抗干扰能力越好。
为了验证振动噪声扰动对输出层神经元膜电位之间相关性的影响,分别将频率为10 Hz、20 Hz、50 Hz的振动噪声加入神经元的输出层中。通过式(13)计算相关系数,相关系数越接近1,噪声干扰对膜电位的影响越小;相关系数越接近0,则噪声对膜电位的影响越大。在不同的振动频率噪声下,噪声对膜电位的影响如图7所示,其中虚线表示陀螺仪在静止状态下输出神经元的触发图,实线分别表示陀螺仪在振动频率为10 Hz、20 Hz、50 Hz噪声干扰下的触发图。右侧为相对应的陀螺仪原始信号与SNN网络处理后的信号图。根据式(13)计算可得,其相关系数分别为0.812 6、0.488 3和0.195 2。由此可知当振动频率强度较低时,前一个神经元和后一个神经元的膜电位相关性较大,噪声干扰对膜电位的影响较小;反之,振动频率较高时,膜电位之间的相关性较小,噪声干扰对膜电位的影响较大。根据以上对比分析以及计算分析可知,基于突触可塑性的SNN网络在随钻振动环境下具有一定的抗干扰能力,可有效处理陀螺仪信号漂移问题。
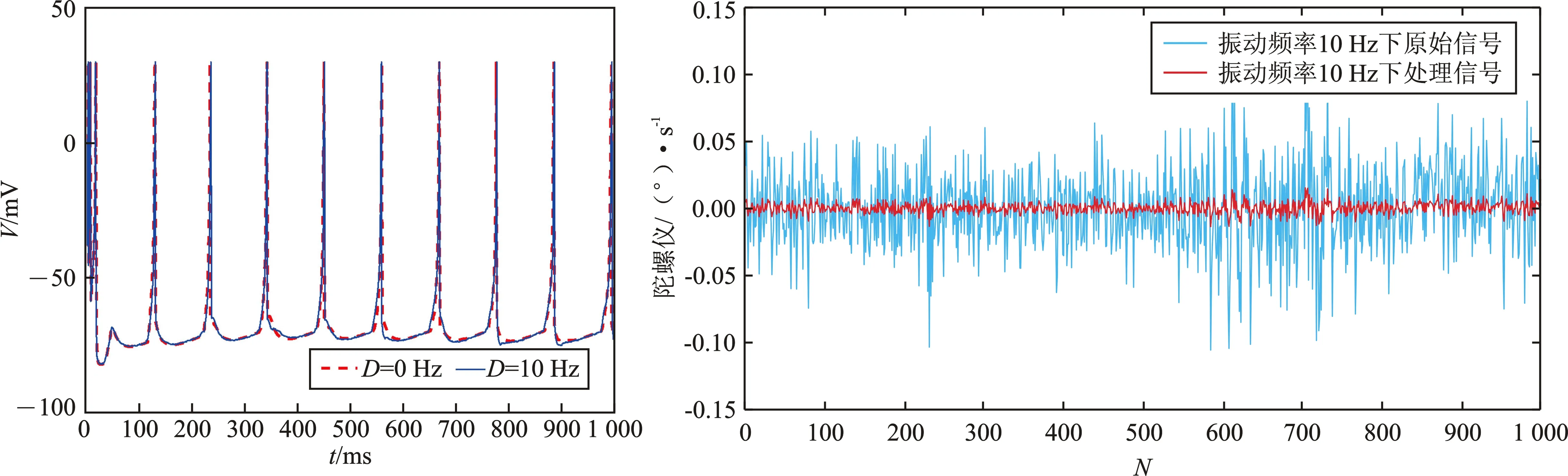
(a)
3 结束语
针对振动噪声严重影响陀螺仪测量精度的问题,本文提出了基于突触可塑性的SNN算法处理振动噪声的影响。通过分析在复杂环境下MEMS陀螺仪随机漂移的误差特性,根据SNN网络仿生物的突触可塑性,调节激发性突触电导和抑制性突触电导,实现在SNN网络下提高陀螺仪信号对噪声的抗干扰能力,实时获取MEMS陀螺仪信号特征。为了验证突出可塑性处理振动条件下陀螺仪信号的有效性,本文通过对比不同振动频率下陀螺仪信号噪声的抗干扰能力,证明了该方法的有效性。
