非理想三相电网的特征信号提取
2022-04-12袁庆庆杨玉美
袁庆庆,蒋 敏,杨玉美
(上海理工大学 机械工程学院,上海 200093)
电网电压畸变和电网电压不平衡是电力系统常见的运行状况,在这种非理想电网情况下会产生大量的奇数次和偶数次谐波以及负序分量,从而影响并网系统的稳定运行。因此,研究非理想电网情况下谐波和负序分量的提取算法具有重大意义[1-2]。
锁相环(Phase Locked Loop, PLL)技术能够实时、有效地检测网络同步信号,因此被广泛应用于负序分量的提取[3-6]。三相同步锁相环(Synchronous Referenceframe Phase-Locked Loop,SRF-PLL)具有易于实现、鲁棒性强、跟踪精度高等优点,已被广泛应用于并网系统。但在电网电压不平衡情况下,锁相环的跟踪性能将受到基频负序电压和高频谐波的影响[7]。因此,许多改进的锁相环技术相继被提出[8-10]。在文献[11]中,采用自适应陷波滤波器在同步旋转结构中产生正交信号,完成了基频正序和负序电压分离。文献[12~13]提出了一种改进的频率自适应锁相环结构,使锁相环能够适应电网电压频率的变化,但是该算法计算量大且实现难度大。由于滑动平均滤波器(Moving Average Filter,MAF)能阻断所有整数倍(1/Tω)的赫兹信号[14],因此,研究人员陆续提出了基于MAF的先进锁相环方法[15-16]。复系数滤波器锁相环(Phase Locked Loop Based on Complex Coefficient Filter, CCF-PLL)是一种较为常用的锁相环结构,它可以快速、准确地提取基频电压的正序分量,从而实现精准锁相。一阶复系数滤波器通常用于实现交叉解耦,但其滤波能力和消除直流偏移的能力有待提高。文献[17]通过改进SRF-PLL中PI(Proportional Integral)控制器集成链路的输出信号,进一步提高了传统CCF-PLL算法的性能。该方法可以在不增加计算量的情况下提高锁相环的锁相性能。文献[18]提出了基于二阶复系数滤波器设计的CCF-PLL,它比一阶复系数滤波器具有更好的谐波抑制能力。文献[19]提出了多阶通用CCF-PLL算法,进一步增强了CCF-PLL的动态特性和滤波能力。
目前比较常用的谐波提取方法包括同步检测法、傅里叶变换法、自适应检测法、小波变换法等[20]。由于傅里叶变换算法结构简单,且谐波提取效果较好,因此成为使用频率最多的谐波提取算法之一[21],其中以滑动离散傅里叶变换(Sliding Discrete Fourier Transform,SDFT)算法和快速傅里叶变换(Fast Fourier Transformation,FFT)算法最为常见。FFT和SDFT都是基于DFT算法的改进,在保留谐波提取效果的同时均加快了算法的运行速率。但是,FFT和SDFT对于特征谐波而言灵活性较低,耗费了不必要的计算时间。同步检测法具有良好的抗扰动性和谐波跟踪效果,但是此手段不利于谐波和正负序无功分量的单独补偿,此外,还存在负载检测时间长等缺点[22-23]。
值得注意的是,以上提出的大多数算法只是抑制了谐波和负序分量其中的一种,然而,在非理想电网环境下这两种特征信号常常同时存在。因此,本文提出了一种基于改进的滑动离散傅里叶变换(Improved Sliding Discrete Fourier Transform,ISDFT)的谐波和负序分量提取算法。与现有方法相比,ISDFT更简单易行,且避免了复杂的参数调整过程。
1 非理想电网的特征
当三相电网电压发生不平衡时,假设不考虑电网电压的谐波分量,则电网电压可表示为基波分量的正、负、零序分量之和,由于电力系统高压架空线路一般采用三相三线制,不存在零序电流通路,因此可以不考虑零序分量的影响,则非理想电网环境下三相电网可分解为三相正、负序等效电路,如图1所示。

(a)
由于只考虑基波分量,则非理想电网情况下的三相电网电压ea、eb和ec可表示为

(1)
以ω作为旋转角频率,把式(1)转化到d-q坐标系下
(2)
式中,ed和eq分别为三相电网电压的d、q轴分量。
由式(2)可知,三相电网电压在d-q坐标系中表现为正序的直流量及负序的二次谐波分量之和。因此,可将三相电网电压在d-q坐标系下的二次谐波分量去除,最终即可得到正序电网电压。
图2为a相电网电压幅值在t=50 ms时降低20%的情况下ed的仿真波形,对应的FFT分析结果如图3所示。综合分析图2和图3可知,当三相电网电压发生不平衡时,ed存在大量的二次谐波。

图2 三相电网电压不平衡情况下ed的仿真波形Figure 2. Simulation waveform of ed under unbalanced three-phase grid voltage

图3 ed的FFT分析结果Figure 3. FFT analysis results of ed
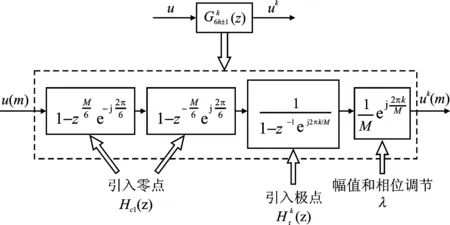
实际上,非理想电网环境下电网电压还存在典型的谐波分量,例如(6h±1)次谐波(h=1,2,3…)。本文基于ISDFT对谐波和负序分量进行提取的结构框图如图4所示。

图4 基于ISDFT的非理想信号分离构框图Figure 4.Block diagram of non-ideal signal separation based on ISDFT

2 改进的滑动离散傅里叶变换算法
2.1 滑动离散傅里叶变换算法
假设v(m)为采样的有限数据序列信号,长度为m,则v(m)的DFT变换为
(3)
其中,WM=e-j2π/M。
式(3)可以进一步表示为
(4)
设v0为第一个采样序列v(0)~v(M-1),v1为第二个采样序列v(1)~v(M),且将v0、v1的DFT变换分别记作V0(k)、V1(k),则SDFT可以表示为
(5)
通过设定式(5)中的k值即可获取k次谐波的幅值。由式(5)进一步可得
(6)
其中,Vm(k)为采样的第m个序列v(m)~v(m+m-1)对应的第k次谐波;Vm-1(k)为第m-1个序列v(m-1)~v(m+m-2)对应的第k次谐波。第m个序列的第k次谐波在时域中可表示为式(7)。
(7)
假设第m个序列为输入信号,所提取的第k次谐波为输出信号,则SDFT在z域的传递函数可表示为
(8)
(9)


图5 SDFT算法的结构图Figure 5. Structure diagram of SDFT algorithm

图6 SDFT算法的零极点图 (M=24,k=5)Figure 6. The pole-zero diagram of the SDFT algorithm (M=24, k =5)
综合以上分析可知,Hc(z)是SDFT的重要环节,主要体现在:(1)Hc(z)决定了哪些谐波能够被完全过滤掉。式(9)表明Hc(z)负责在整数倍基频处引入M个零点,如ω=λω0(λ=0,1,…,M-1)。因此,所有的整数次谐波都可以被完全滤除;(2)Hc(z)决定了谐波提取的响应速率。由于Hc(z)结构中的M个延时缓冲器引入了M个零点,考虑到实际三相电网中几乎不存在偶数次谐波,所以M个零点的引入会导致不必要的时延,这就是传统SDFT的不足。
2.2 改进的滑动离散傅里叶变换算法
为了更灵活、更快速地提取特征次谐波,本文对Hc(z)进行了重新设计。由于非理想电网电压包含的谐波主要为k=6h±1次(h=1,2…)和k=2次谐波,因此将z=z1/6e-j2π/6M,z=z1/6ej2π/6M和z=z1/2分别代入到式(9)中,则Hc(z)被重新设计为
(10)
(11)
联立式(10)和式(8)可得
(12)
(13)

(a)

(a)
3 实验结果
实验平台如图9所示,从左至右依次为:(1)模拟非理想电网环境(三相电网电压畸变和不平衡)的可编程三相交流源;(2)用于处理ISDFT算法的TMS320F28335 DSP信号处理系统;(3)显示实验结果的示波器。

图9 实验平台Figure 9. Experimental platform
3.1 信号跟踪性能
假设输入信号为uin=sin(500πt),由DFT、SDFT、ISDFT分别对uin进行提取,实验结果如图10所示。

图10 基于DFT、SDFT、ISDFT的信号提取对比(静态) Figure 10. Signal extraction and comparison based on DFT, SDFT, ISDFT (Static)
由图10可知,ISDFT的静态响应时间约为2个周期,而SDFT和DFT的静态响应时间约为5周期,即ISDFT的静态响应时间约为DFT和SDFT的1/3,与理论分析一致。
图11为动态情况下DFT、SDFT、ISDFT跟踪uin的仿真结果。图中,当t=0.2 s时uin的幅值增倍(1 V→2 V)。

图11 基于DFT、SDFT、ISDFT的信号提取对比(动态)Figure 11.Signal extraction and comparison based on DFT, SDFT, ISDFT (Dynamic)
由图11可知,ISDFT的动态响应时间约为两个周期,SDFT和DFT的动态响应时间约5个周期,即ISDFT的动态响应时间约为DFT和SDFT的1/3。综合分析图10及图11可知,DFT、SDFT、ISDFT对信号检测的能力相同,但ISDFT比DFT和SDFT的运行速率更快。
3.2 谐波提取
利用可编程三相电源对a相电网电压注入5次谐波,得到的三相电网电压如图12(a)所示。图12(b)为基于ISDFT提取的5次谐波。图12(c)为5次谐波被分离后的三相电网电压。

(a)
综合分析图12可知,当对a相电网电压注入5次谐波后,三相电网电压发生了明显畸变,在ISDFT的作用下,5次谐波得以被快速、准确地提取,响应时间约为10 ms。
以提取三相电网电压的5次、7次谐波为例,表1和表2分别对DFT、SDFT、ISDFT的响应时间和提取效果进行了对比。由表1可知,ISDFT的响应速率比SDFT快了44.56%,比DFT快了65.32%。由表2可知,DFT、SDFT、ISDFT提取谐波的效果相同。
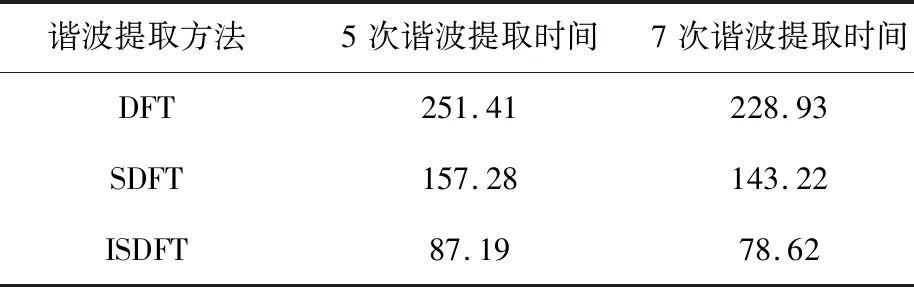
表1 谐波提取时间比较Table 1. Comparison of harmonic extraction time /μs

表2 谐波提取效果比较Table 2. Comparison of harmonic extractionresult /%
3.3 负序分量提取
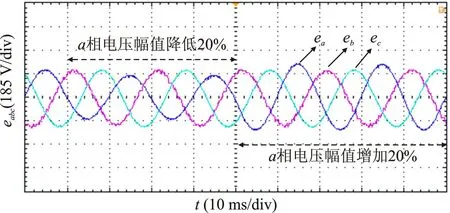
图13(a)为a相电网电压幅值发生突变的三相电网电压。图13(b)和图13(c)分别为基于ISDFT提取的三相电网电压的d、q轴负序分量。图13(d)为负序分量被分离后的三相电网电压。由图13可知,当三相电网电压发生幅值不平衡时,ISDFT能快速、有效地提取负序分量,响应时间约为10 ms。
(a)
图14(a)为a相电网电压相位发生突变的三相电网电压。图14(b)和图14(c)分别为基于ISDFT提取的d、q轴负序分量。图14(d)为负序分量被分离后的三相电网电压。综合分析图14可知,当三相电网电压发生相位不平衡时,ISDFT在能够在10 ms内提取负序分量,并使得三相电网电压重新恢复平衡。

(a)
图15(a)为a相电网电压频率发生突变的三相电网电压。图15(b)、图15(c)分别为基于ISDFT提取的d、q轴负序分量。图15(d)为负序分量被分离后的三相电网电压。由图15(a)可知,当电网发生频率突变时,会使得三相电网电压相位发生不平衡。综合分析图15可知,当电网电压频率发生变化时,ISDFT同样具备快速、准确地提取负序分量的能力,响应时间同样约为10 ms。

(a)
综合图13~图15可以看出,当三相电网电压因幅值、相位、频率的改变而引发电网不平衡时,ISDFT均能快速且准确地提取负序分量,响应时间约为10 ms(半个周期)。
3.4 负载突变情况下的负序分量提取
图16(a)为不平衡电网情况下(三相电网电压幅值不平衡)发生三相负载突变的三相电网电压。图16(b)、图16(c)分别为基于ISDFT提取的d、q轴负序分量。图16(d)为负序分量分离后的三相电网电压。图16表明,当三相不平衡电网发生负载突变时ISDFT具有较好的动态性能,动态响应时间大约为14 ms。

(a)
4 结束语
本文针对非理想三相电网存在的谐波以及负序分量这一问题提出了基于ISDFT的特征谐波和负序分量提取算法。该算法通过对SDFT传递函数进行重新设计,在保留良好的信号过滤特性同时提高了信号提取的速度和灵活性。本文分别从信号跟踪性能、谐波提取以及负序分量提取3个角度进行了实验分析,实验结果表明,提出的ISDFT算法不仅能快速、准确地提取谐波和负序分量,而且具有良好的动态性能。此外,以提取三相电网电压的5次、7次谐波为例,DFT、SDFT、ISDFT提取谐波的效果一致,但ISDFT的响应速率比SDFT快44.56%,比DFT快65.32%。
