一道不等式问题的错因探究

黄平海

(江西省赣州市崇义中学，341300)

在听课过程中,我发现不少老师讲课时淡化知识的形成过程,只注重知识的运用,通常一节课花几分钟讲完了公式或定理等知识,剩下的时间用来讲例题和练习.慢慢地,学生做题也是重结果轻过程.这样的教学若长期以往,则既不利于培养学生的钻研精神,更不能培养学生的核心素养,甚至会使学生解题时出现科学性的错误.

下面以一道不等式问题为例,学生的两种解法过程都看似正确,但哪一种是错误的?错在哪里?

题目设1≤x+y≤4,-2≤x-y≤-1,求2x-3y的取值范围.

解法1由条件可知

1≤x+y≤4,

①

-2≤x-y≤-1.

②

现在将①+②,① -②,可得

③

1≤y≤3.

④

又③×2,④×3,可得

-1≤2x≤3,

⑤

3≤3y≤9,

⑥

⑤ -⑥,得

-10≤2x-3y≤0.

⑦

综上,2x-3y∈[-10,0].

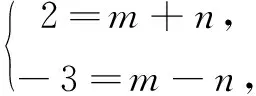
又由条件,可知

⑧

⑨

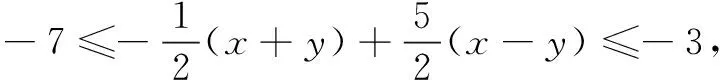
反思两种解法,结果不同.哪一种解答错了?

那么,解法1到底错在哪里?为了探个究竟,我们可以把x,y当作变量,已知两个二元一次不等式成立,要求2x-3y的取值范围,问题就可以用线性规划的方法来解决.

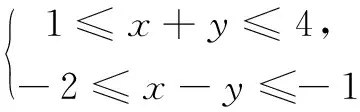
综上,2x-3y∈[-7,-3].

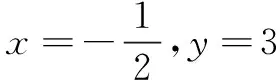
究其本质,条件不等式① 和② 组成的不等式组与③ 和④ 组成的不等式组不等价,利用图1可以清晰地看到这一点.我们在求解线性规划问题时,一定要注意准确利用自变量的取值,确保目标函数的最值必须在可行域内取得.