高考试题谋创新开放 课堂教学促数学理解——2021年高考创新性试题分析与教学启示

王 丽

(江苏省扬州大学数学科学学院,225002)

2021年高考落下帷幕,为推进新高考的稳步进行,教育部命题中心命制了6套高考数学试卷,分别为全国甲卷(文、理)、全国乙卷(文、理)、新高考Ⅰ卷以及新高考Ⅱ卷,自主命题的省份有北京、天津、上海、浙江4个省份.“注重数学创新意识”是高考数学命题指导思想之一,今年的十套高考试卷聚焦核心素养,彰显立德树人的核心要求,以创新意识、问题解决为价值取向,试题背景新颖、创新,强化对学生思维能力的考查.通过创新题的设计,克服通过刷题与机械记忆提升分数的做法,数学课堂教学突出对数学的理解.本文以2021年全国各省高考数学卷为例,聚焦高考试题创新之处,落地数学课堂教学.

高考数学试题创新,新在试题背景情境、试题知识交汇、试题创新定义、试题设问开放以及试题的思维容量,考查学生数学阅读理解、数学探究、创新意识以及综合运用数学知识与思想方法的能力.

一、创新性试题解析

1.新情境

2021年高考命题十项原则中的第一条原则要求“方向明确,立意鲜明,情景新颖,贴近实际”[1].问题情境的设置要以真实的生活背景或是历史背景为依据,引导学生关注生产生活与社会发展,以数学的眼光观察世界.今年各省高考卷情境创设紧密联系实际.如新高考Ⅰ卷第18题以“一带一路”知识竞赛为背景,考查概率统计知识与数据分析素养,引导学生关注社会经济发展;全国乙卷(理)第9题以魏晋时期刘徽撰写的《海岛算经》中海岛的高的测量方法为背景,展现我国数学发展史上古人的伟大贡献,考查学生知识综合运用能力;上海卷第1题以上海第十届花博会为背景,引导学生关注社会发展,考查概率知识掌握等.

例1(2021年全国甲卷理科第2题)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图(图1):

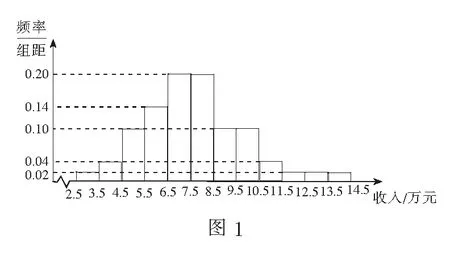
根据此频率分布直方图,下面结论中不正确的是( )

(A)该地农户家庭年收入低于4.5万元的农户比率估计为6%

(B)该地农户家庭年收入不低于10.5万元的农户比率估计为10%

(C)估计该地农户家庭年收入的平均值不超过6.5万元

(D)估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间

解低于4.5万元的比率估计为0.02×1+0.04×1=6%,故A正确.同理计算其余选项,可知不正确的只有选项C.

评注2020年是我国脱贫攻坚的决胜之年.本题以我国乡村振兴、脱贫攻坚工作中调查农村家庭经济收入情况为背景,与时代背景紧密联系,在考查学生分析问题、解决问题的同时,考查学生数据分析素养,以背景情境引导学生关注我国社会进步,增强学生民族自豪感与自信心.

2.新交汇

基于知识交汇的题型将不同的知识点相结合,进行综合考查,很好地凸显了高考数学试题强调知识的融会贯通这一要求.在知识交汇处设置问题体现了知识的纵向联系以及不同知识板块的横向联系,对学生的创新意识、知识梳理与综合运用能力以及数学核心素养有着全方位的考查.

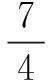
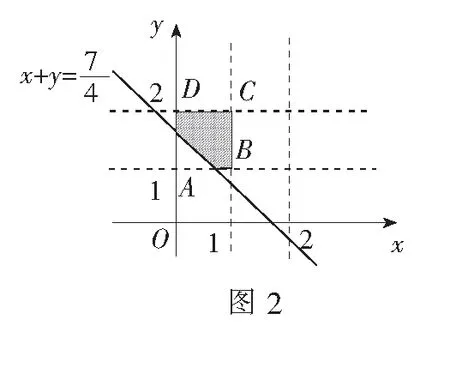
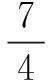
评注一般线性规划通常与不等式、三角以及数列内容相结合,考查极值问题.本题充分利用线性规划的包容性,创新地将其与几何概型相交汇,考查学生数形结合思想,在充分理解线性规划与几何概型实质的基础上完成本题的解答.

3.新定义

高考中常借助新定义问题考查学生的应用意识与创新意识.新定义问题融知识、方法及思维于一体,融合度高,通常定义一个教材中从未涉及的新概念、新运算等[2],需要学生通过阅读理解并结合已有知识完成问题解答,综合考查学生的数学阅读理解与数学分析能力.如今年的上海卷和北京卷均以新定义题型作为压轴题,考查学生分析问题、解决问题的能力.

例3(2021年上海卷第21题)已知f(x)是定义在R上的函数，如果对任意x1,x2∈R,x1-x2∈S,都有f(x1)-f(x2)∈S,则称f(x)是S关联.

(1)判断和证明f(x)=2x+1是否是[0,+∞)关联？是否是[0,1]关联？

(2)f(x)是{3}关联，当x∈[0,3)时，f(x)=x2-2x,解不等式2≤f(x)≤3;

(3)证明：“f(x)是(1)关联，且是[0,+∞)关联”当且仅当“f(x)是[1,2]关联”.

解(1)任取x1,x2∈R，若x1-x2∈[0,+∞)，则f(x1)-f(x2)=2x1+1-(2x2+1)=2(x1-x2)∈[0,+∞)，故f(x)=2x+1是[0,+∞)关联.

若x1-x2∈[0,1]，由f(2)-f(1)=2∉[0,1]，得f(x)=2x+1不是[0,1]关联.

(2)由f(x)是{3}关联，得x1-x2=3时，都有f(x1)-f(x2)=3,即f(x+3)=f(x)+3.

(3)必要性.

由f(x)是{1}关联，得f(x+1)=f(x)+1.由f(x)是[0,+∞)关联，得对任意x1≥x2,有f(x1)≥f(x2),即f(x)是单调增函数.因此，若1≤x1-x2≤2,则1+x2≤x1≤2+x2，由f(x)为单调增函数，得f(x1)-f(x2)≥f(1+x2)-f(x2)=1,且f(x1)-f(x2)≤f(2+x2)-f(x2)=f(1+x2)+1-f(x2)=2.所以f(x)是[1,2]关联.

充分性.

若f(x)是[1,2]关联，则

1≤f(x+1)-f(x)≤2,

①

1≤f(x+2)-f(x)≤2,

②

1≤f(x+2)-f(x+1)≤2.

③

于是-2≤f(x+1)-f(x+2)≤-1,与②相加，得-1≤f(x+1)-f(x)≤1.由此结合①式，可得f(x+1)-f(x)=1,即f(x)是{1}关联.

由f(x+1)=f(x)+1,递推得f(x+n)=f(x)+n,n∈Z.因此，若x1-x2≥0,则必有x1-x2∈[k,k+1),k≥0,k∈Z.进而1≤x1-x2+1-k≤2,即1≤x1-(x2+k-1)≤2,由f(x)是[1,2]关联，可得1≤f(x1)-f(x2+k-1)≤2,即1≤f(x1)-f(x2)-k+1≤2,得f(x1)-f(x2)≥k≥0,即f(x)是[0,+∞)关联.

综上,问题得证.

评注本题给出一个新函数的概念,第(1)问是新函数定义的熟悉理解;第(2)问通过数形结合的方法引导学生发现函数是一个类周期函数并快速求解问题,考查学生运用新概念解决问题的能力;第(3)问则需要学生在理解新概念性质的基础上,从必要性和充分性两个方面着手分析和解决问题,考查学生运用新概念解决抽象数学问题的能力,对学生数学素养的考查更进一步.本题通过层层递进的三个问题,加深学生对数学知识的理解与应用,不仅考查学生数学阅读、数学抽象、逻辑推理等能力,还对学生数学理解能力提出较高要求.

4.新设问

2021年的高考数学试题积极贯彻“改变相对固化的试题形式,增强试题开放性”的原则[3],各省高考试题加大题型的创新,设问开放,开放性试题在各省高考卷中频频出现.开放式试题一般以条件开放、结论开放或者条件结论都开放的形式出现.如全国乙卷理科第16题、新高考Ⅱ卷第14题的举例开放题,条件确定,结论开放,考查学生思维的灵活性;新高考Ⅱ卷第22题、北京卷第16题,条件开放,结论确定,考查学生对数学本质的理解;全国甲卷理科第18题的条件结论均开放,考查学生严密的逻辑推理能力.此类开放性试题是高考数学考查学生核心素养的路径之一,逐渐在高考卷中崭露头角,未来也必然是高考数学考查趋势.

例4(2021年新高考Ⅱ卷第14题)写出一个同时具有下列形式①②③ 的函数f(x):______.①f(x1x2)=f(x1)f(x2);② 当x∈(0,+∞)时，f′(x)>0; ③f′(x)是奇函数.

解可取f(x)=x2,f(x)=x4,…,等等.

评注本题属于条件确定,结论开放型试题,需要学生在明确条件要求的基础上给出相应结论,此类题型结果较多,学生列举其中一个即可.条件② 表明该函数在(0,+∞)单调递增,由条件③ 可得该函数的原函数是一个偶函数,结合这两点以及条件① 的要求,结果就逐渐清晰.此类开放题主要考查学生逻辑推理能力以及数学探究能力,对学生理性思维要求较高.

5.新思维

中学数学的教学除了知识的传授外,更重要的是数学思维的培养.新高考为了引导减少数学“死记硬背”的情况,在立足基础知识的前提下,加大对学生探索性思维能力的考查.如北京卷第14题三角函数题,学生可根据三角函数在单位圆上的定义求解,也可以通过诱导公式结合三角函数图象求解;新高考Ⅱ卷第20题立体几何题第(2)问,学生可考虑建立空间直角坐标系,利用向量将几何问题代数化,这样的解法较为常规,对运算能力要求较高,学生也可以通过立体几何空间感找出二面角的位置,进而解决问题,这对学生直观思维要求较强.不同的思维角度对学生探究问题、分析问题、解决问题的能力有很大影响,对学生在考场能否快速寻得最优最简便的方法至关重要..

例5(2021年新高考Ⅰ卷第13题)已知函数f(x)=x3(a·2x-2-x)是偶函数，则a=______.

解法1定义法

依题意,f(x)=f(-x)，即x3(a·2x-2-x)=-x3(a·2-x-2x)，故(a·2x-2-x)=-(a·2-x-2x)，即(a-1)(2x+2-x)=0,可得a=1.

解法2特殊值法

解法3函数性质

由y=x3是奇函数，f(x)是偶函数，得y=a·2x-2-x是奇函数.又y=2x-2-x是奇函数(联想常见形式y=ex-e-x),故a=1.

评注本题是一道基础题,利用偶函数的定义,通过运算就可以得到答案,虽然题目简单,但运算出错也会致使该题失分.特殊值法以及利用熟悉的y=ex-e-x及函数奇偶性均能够快速得出结果,尤其解法3需要学生有敏锐的数学直觉,而这样的数学直觉就依赖于数学学习过程中的类比、归纳和联想能力与数学思维.

二、教学启示

1.合理情境引入,挖掘史料价值

在“五育并举”的大背景下,“死读书,读死书”是万万不可取的.教师应当引导学生切实关注时事热点,关注社会发展.在课堂中对问题情境的引入也须合理真实,结合生产生活实际,体现时代气息.在教学中要重视数学史的育人价值,以史为题,以史促学,挖掘数学知识的形成与发展过程,促进学生对知识背景的理解.

2.立足知识整体,探究知识本源

知识交汇题型的出现充分表明知识联系的重要性,是对学生数学关键能力的考查.碎片化的学习已然适应不了终身学习与社会发展的需求,教师在教学过程中要立足知识整体,以“知识覆盖”转向“观念统领”，追求数学本质,引导学生围绕数学核心内容开展知识本源探究,进而促进学生数学理解.

3.发展核心素养,构建知识网络

新定义题的出现落实了检测学生数学核心素养的要求,新定义题融合度高,因此对学生归纳概括、数学推理以及知识的灵活运用提出较高要求.在新高考的背景下,题海战术显然已不可取,教师在教学过程中应当引导学生多思考、善表达,给予学生充分数学交流的机会,重视学生数学知识的归纳总结与数学核心素养的发展,注重知识网络的构建.

4.多设开放问题,强化数学推理

开放性问题重在考查学生数学抽象、逻辑推理核心素养,开放性问题的出现让数学不再“冷冰冰”,并为其增添了一丝趣味.因此,教师在教学过程中要重视开放性问题的提出,多设置开放性问题,引导学生发散思维;拓宽教学思路,丰富教材内容,唤醒学生开放意识;加强开放性问题练习,强化数学推理能力.

5.调动思维能力,促进数学理解

“学而不思则罔,思而不学则殆”恰到好处地表明了学与思的关系,数学学习是建立在思考的基础之上的.教师的教学除了教材上的知识外,更要挖掘教材知识的本质内容,为学生创设探索数学的路径,教会学生数学思维的方法,调动学生内在的思维能力,促进学生数学理解,形成良好的思维品质.