尝试探究 启迪思维—— 一节助力思维深化的圆锥曲线复习课

陈 静

(江苏省扬州市扬州大学附属中学，225002)

一、引言

圆锥曲线是高考考查的重点内容,其中定点定值问题更是高考的热点.2017年高考数学全国卷I理科第20题,是研究圆锥曲线的定点定值问题的好素材.这道题蕴含丰富,意境深远,具有较强的再生能力,较广的发展空间,对其进行深入探究有利于提升学生解决定点、定值问题的能力.笔者围绕该问题设计了一节复习课,引导学生探究多种解题策略,渗透思想方法,激活数学思维,培养创新意识,发展学生的逻辑推理、数学运算等核心素养,取得了良好的效果.

二、试题呈现

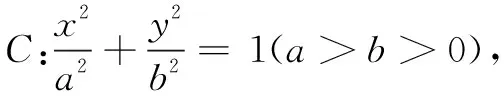
(2)设直线l不经过点P2且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.

三、分析探究

师:这道高考题的第(2)问考查直线过定点,同学们有怎样的解题策略?

生1:(方法1)从特殊到一般,先选取直线l两个特殊位置,它们的交点即为定点,再证明这个定点与变量无关.

生2:(方法2)从一般性出发,设直线l的方程为y=mx+n,寻找参数m,n之间的数量关系,从而得到直线过定点.

师:很好,这是解决直线过定点问题常用的两种方法,请同学们动笔尝试解决.

设计意图通过教师的引导,学生明确解题思路,调用基本活动经验,尝试解答问题.

师:如何选取直线l两个特殊位置?

师:如何证明一般性呢?

师:上述解答过程有不严密之处吗?

师:补充得很好,考虑问题很全面!

设计意图教师帮学生厘清思路,引导思考方向，通过小组互助,学生自己动手演算解题,提升课堂执行力,提高课堂效率.教师适时点出学生的思维漏洞,引发学生深入思考,完善解题过程.

师:直接从一般性出发能解答这个问题吗?

生5:设A(x1,y1),B(x2,y2),直线l的方程为y=mx+n,将其与椭圆方程联立,由斜率之和为-1,利用韦达定理求出m,n的数量关系,即可得出直线l过的定点.

师:分析很到位!请同学们根据该思路,在演算纸上尝试答题.

师:解答得非常漂亮!当然,也要补充说明直线l斜率不存在的情况.

设计意图在通过运算解决问题的过程中,形成正确的运算思路是解决问题的关键.只有理解解决问题的思路,才能掌握一类问题的通性通法[1].教师引导学生算思并举,设计合适的运算思路、运算程序,促进学生数学思维发展,提高运算效率,提升运算素养.

师:这个想法很有思考性!该式可以整理成关于k的方程(4n+4)k2-8mk+n-1=0,再结合直线P2B与椭圆的交点B也在直线y=mx+n上,同学们能够联想到什么?

生7:直线P2A和直线P2B的斜率应该是该方程的两根.

师:理解得非常透彻!一元二次方程根的问题,通常可以考虑用韦达定理,根据直线P2A与直线P2B的斜率的和为-1,你可以得到什么?

师:很精彩!同学们有着良好的理解能力,较强的观察能力、联想能力,这些都是学好数学的有力保障!

设计意图教学过程中,充分展示学生关于问题的思考过程,学生思路受阻时,在教师的启发、点拨下，学生通过观察、联想、推理、发散思维,得到另一种解法.只有及时发现学生思维的“闪光点”和“障碍点”,才能让学生掌握新的方法;只有发展了学生的思维,才能提升学生的解题能力[2].

师:在本题中,由直线P2A与直线P2B的斜率的和为-1,可证得直线l过定点.据此,你有什么启发和猜想?

生9:直线P2A与直线P2B的斜率的和为其他数值,比如1,直线l是否仍然过定点?

师:请同学们在上述方法中选择一种,探究该问题.

师:同学们有一般性的猜想吗?

生11:直线P2A与直线P2B的斜率的和为常数λ,直线l过定点.

生12:直线P2A与直线P2B的斜率的积为常数λ,直线l过定点.

师:非常好,请同学们小组合作,探究这两个猜想是否成立(投影展示小组合作成果).

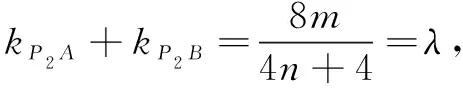
师:这个猜想非常大胆,也很有探究性!将以上问题推广到更一般的情况,结论也成立.

四、推广及变式

1.推广

设计意图教师有意识地引导学生从特殊到一般去发现结论、推广命题,培养学生类比迁移、发现问题与提出问题的能力,发展探索精神、创新精神.

2.变式

师:在上述推广中,如果条件和结论互换一下,同学们可以得到什么结论?

设计意图利用条件与结论的互换,对上述推广进行了变式探究,借助对知识的拓展与探究,学生既熟悉了处理定点定值的方法,也学会了将知识引申拓广的方法.

五、延伸拓展

(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得DQ为定值.

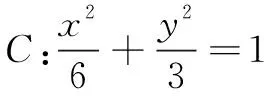
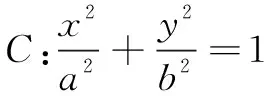
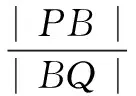
评注由逆命题1,得

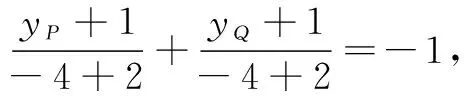
设计意图选择合适的高考试题进行拓展练习,让学生通过多方位的观察思考,广泛联系所学知识,去寻求分析和解决问题的思路和方法,可以促使知识融会贯通,提升思考问题的能力[3],促进逻辑推理素养的形成.