非对称结构问题的类型与处理策略——例谈韦达定理在解析几何中的应用

韩晓慧

(安徽省阜阳市第三中学，236031)

类型1比值类

解若直线l的斜率存在,设其方程为

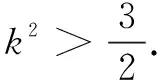
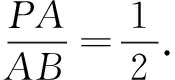
类型2线性类

此类问题的难点是出现线性关系式mx1+nx2=λ(λ≠0)或my1+ny2=λ(λ≠0)为非对称结构,求解时可将线性关系式先变形,再用配对法处理问题.

例2已知直线l过抛物线y2=4x的焦点F,与抛物线交于A,B两点,则当|FA|=3|FB|时,求直线l的方程.

类型3不对称分式类

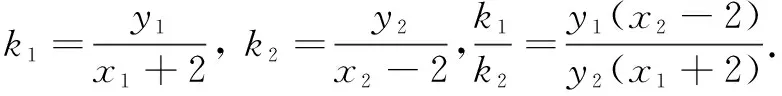
策略1和积转换法

此类解题策略是找出y1+y2与y1y2的关系,在变式转化中解决问题.

策略2半代换配凑法

此类解题策略是目标函数中对能代换的部分先用韦达定理进行代换,再对剩余部分进行选择性配凑,使问题获解.

评注(1)对分母作类似处理同样可获解.(2)以上解法是对纵坐标进行配凑半代换,借助横坐标进行配凑半代换亦可证明,读者可自行尝试.

策略3先猜后证法

此类解题策略是先由特殊情况得到定值,再证明一般情形也为该定值.

策略1与策略2是用韦达定理处理结构为非对称类问题的两种有效方法,而猜证结合也是探究这类题型的常见处理手段.通过上述例题我们也能感受到,不同的参数引入和直线假设,对后续的计算处理将产生不同的影响,计算量也存在较大差异.