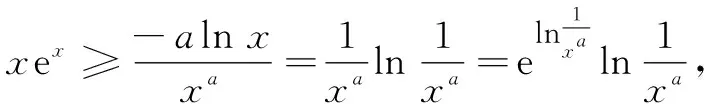同构法巧解指数与对数共存的函数问题

程 伟

(江苏省南京师范大学附属扬子中学，210048)

在求解方程或者恒成立问题求参数范围以及证明不等式成立时,若遇见指数与对数函数共存的等式或者不等式,采用隐零点代换、参变分离或者直接求导难以避免繁琐计算,有时甚至很难进行下去,但若考虑采用同构法进行转化,把等式或者不等式等价变形,使其两侧结构一致,就能够找到一个函数模型,再利用函数的单调性化繁为简,加快解题速度.

一、同构法在恒成立或能成立问题中的应用

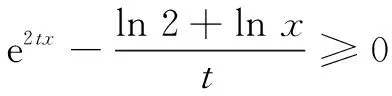
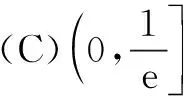
解法1题设不等式即te2tx≥ln 2x,即2txe2tx≥2xln 2x,亦即2txe2tx≥(ln 2x)eln 2x.

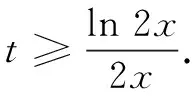
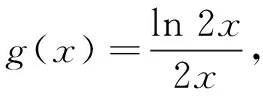
故选B.

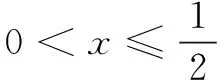
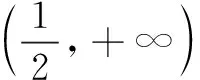
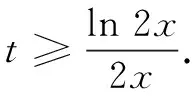
评注对于aea≥blnb型指数对数共存不等式,同构方式有三种:(1)以左侧为基准,变形得aea≥lnbeln b,构造函数y=xex;(2)以右侧为基准,变形得ealn ea≥blnb,构造函数y=xlnx;(3)取对数得lna+a≥ln(lnb)+lnb,构造函数y=x+lnx.

本题三种方式中,取对数法构造的函数单调性判断最简单.

例2(2020年全国高考题)已知函数f(x)=aex-1-lnx+lna.

(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成三角形的面积;

(2)若f(x)≥1,求a的取值范围.

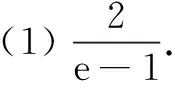
(2)f(x)≥1等价于eln a+x-1+lna+x-1≥lnx+x=eln x+lnx.令g(x)=ex+x,则上述不等式等价于g(lna+x-1)≥g(lnx).又g(x)显然为单调增函数,故lna+x-1≥lnx,即lna≥lnx-x+1.

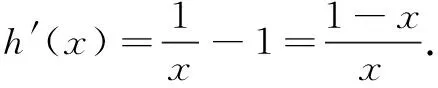
于是lna≥0,得a≥1，即a的取值范围为[1,+∞).

评注对于ea±a≥b±lnb型指数对数共存函数问题,同构方式有两种:(1)以左侧为基准,变形得ea±a≥eln b±lnb,构造函数f(x)=ex±x;(2)以右侧为基准,变形得ea±ln ea≥b±lnb,构造函数f(x)=x±lnx.

二、同构法在证明不等式中的应用

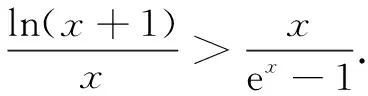
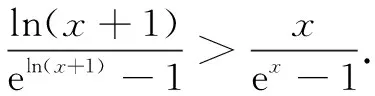
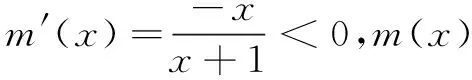
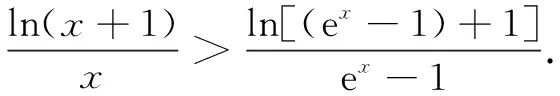
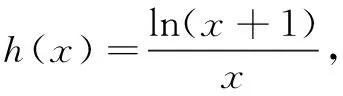
由导数法易知ex>x+1(此处略),故原不等式得证.

三、同构法在隐零点问题中的应用

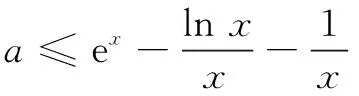
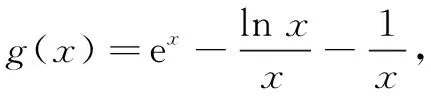
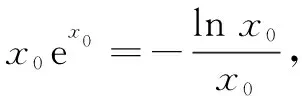
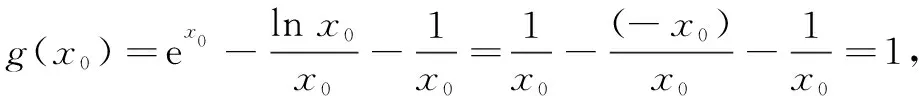
评注在本题隐零点问题中,因方程不可解,可考虑等价化成aea=blnb型指数对数共存函数,采用与左侧同构方式变为aea=lnbeln b,构造函数p(x)=xex,使问题获解.

四、同构法与切线不等式结合求解最值问题

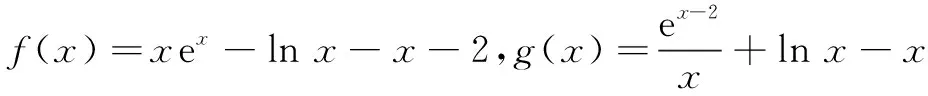
(A)a=b

(B)a

(C)a>b

(D)a,b的大小关系不确定

分析本题若用导数法直接求出f(x),g(x)的最小值,则需多次求导,过程较繁.采用同构法与切线不等式相结合进行求解,可大大简化解题过程.

同理可得g(x)=ex-2-ln x+lnx-x≥(x-2-lnx+1)+lnx-x=-1,当且仅当x-2=lnx时取等号,b=-1.故选A.

所以a∈(-∞,1].

评注通过例4、例5的解法,可以发现同构和切线不等式放缩ex≥x+1和lnx≤x-1相结合具有很强的威力,能明显提升解题速度.利用常见模型xnex=ex+nln x≥x+nlnx+1能有效实现指数与对数互化,解决相应问题.