多先验融合的显著性检测*

常 振 段先华 鲁文超

（江苏科技大学计算机学院 镇江 212003）

1 引言

人类视觉系统可以快速对场景中最引人注意的物体或区域定位，计算机通过模仿这一视觉系统形成显著性检测技术。显著性检测算法可以分为两大类：自底向上［1］的显著性检测算法和自顶而下［2］显著性检测算法。自底而上的检测模型以待检测区域的低级特征为基础进行分析、处理。通过这类算法获得的显著图更清晰。而自顶而下的模型利用高层语义知识对算法进行指导，使得算法能够更好地检测显著区域。但由于自顶向下显著性检测算法通常只适用于特定场景，所以对其研究比较少。而自底向上显著性检测算法因其简单、快速等原因，更受广大研究者的青睐。

早期Itti 等［3］利用亮度，颜色和方向三个特征，结合多尺度分析计算出显著图。Hou等［4］利用频率域进行处理，其基本原则是抑制频繁出现的特征响应，同时对变化的特征保持敏感。Liu 等［6］将对比度，先验知识和全局区域相似性结合起来，在层次分割的基础上生成显著图，有效地利用了局部对比的信息，但该算法趋向于关注边缘信息，导致了显著区域不明显的问题。基于此，Cheng 等［7］利用全局对比度来计算图像中每个像素的显著值。首先对图像进行超像素分割，然后计算区域和颜色对比度，再利用每个区域和其他区域的对比度加权和来计算显著值。Lu 等［8］利用贝叶斯模型提出一种快速的自底向上的显著性检测模型。该方法首先通过凸包获得初始显著区域，然后利用拉普拉斯稀疏子空间聚类算法对局部特征的超像素分组，计算先验图，最后利用凸包计算似然概率，并通过贝叶斯模型融合得到最终显著图。

在复杂背景下，文献［9］通过边界连通性计算超像素的背景概率存在误差，不够精确。针对上述问题，本文算法在背景先验的基础上进行改进，提出多先验融合的显著性检测算法：1）通过SLIC 算法将图像分割成四种不同的尺度；2）分别对不同尺度图像的上、下、左、右边界显著图进行计算，并对其进行加权融合得到边界先验；3）依据边界信息、颜色信息和空间距离信息计算背景显著图；4）利用元胞自动机计算出显著图，并将背景显著图和元胞自动机显著图进行融合得到背景先验；5）通过颜色归一化，计算图像颜色先验；6）利用多层元胞自动机对三个先验图进行融合，得到最终显著图。本文算法流程图如图1所示。

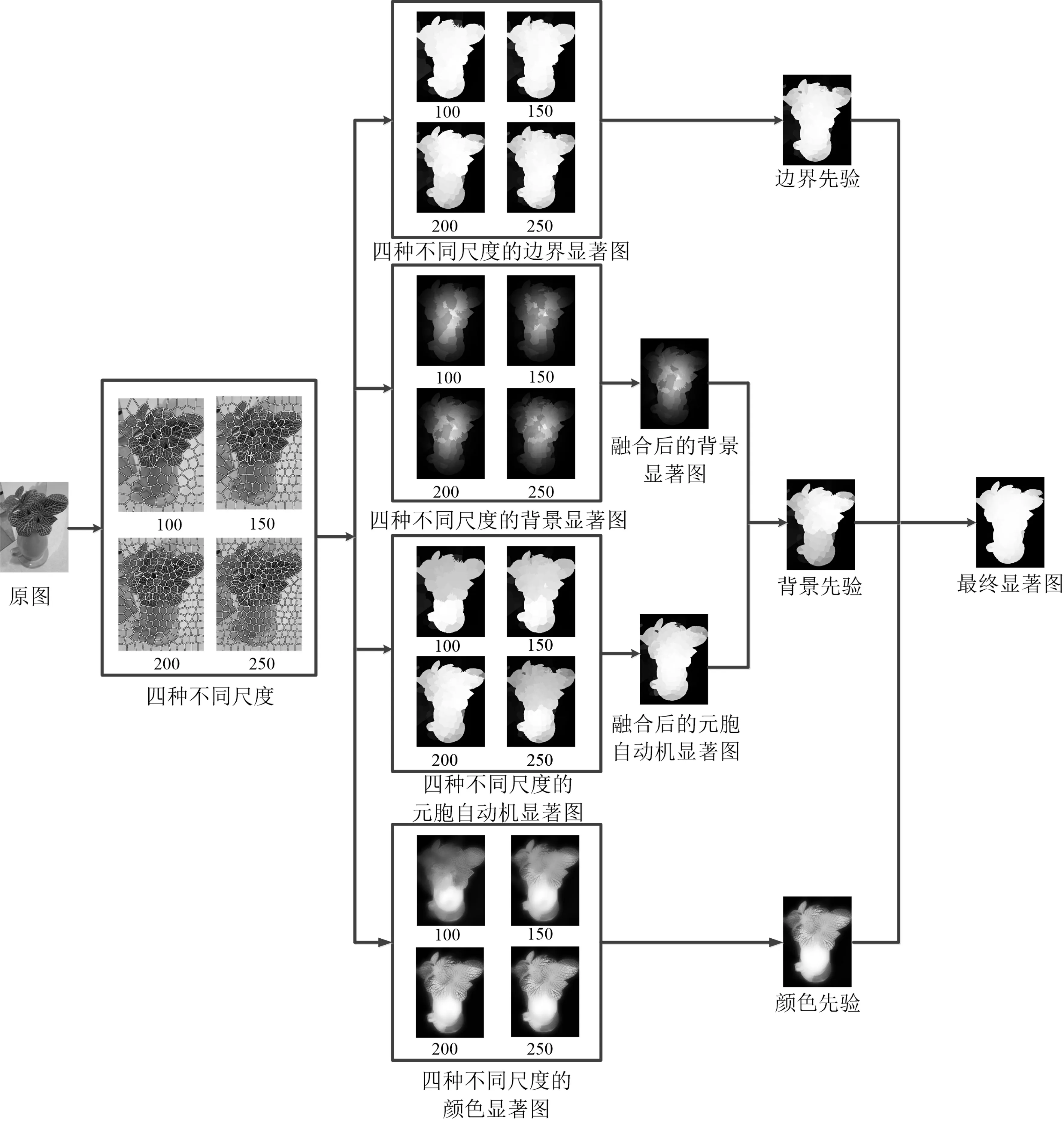
图1 算法流程图

2 多先验融合算法

2.1 边界先验

流形排序算法［10］以超像素为节点构造图模型，并选取某些节点为查询节点，然后利用目标函数最小值计算每个节点排序值，将此排序值定义为节点显著值。具体算法描述如下。

1）给定一组数据集：X={x1，x2，…，xn}∈Rm×n，其中m 是超像素节点所对应的特征维数，n 是超像素节点个数，其中包括部分被标记的查询节点。

2）定义排序函数F：X→Rn，相当于查询对象给每个待排序的未标记数据xi分配排序值fi。

3）令指示向量Y=[y1，y2，…，yn]T对数据的标记情况进行记录，其中当yi=1时，表示对应的数据xi为查询节点，当yi=0 时表示对应的数据xi为待标记数据，且xi的值由F确定。

4）构建图模型G=(V，E)，其中V由数据集X构成，图的边缘E是利用关联矩阵W=[wij]n×n计算，计算图的度矩阵D=diag{d11，…，dnn}，其中dii和wij分别由式（1）和式（2）计算：

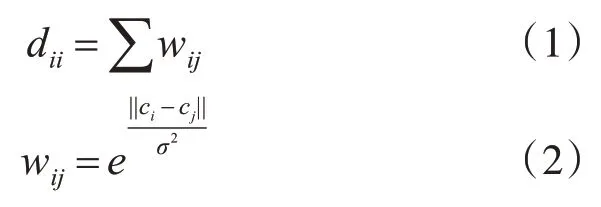
其中ci和cj代表在CIELab颜色空间中两个节点的超像素的平均值，σ是控制边权重的常数。

5）对于给定查询对象的排序得分可由式（3）计算得到：

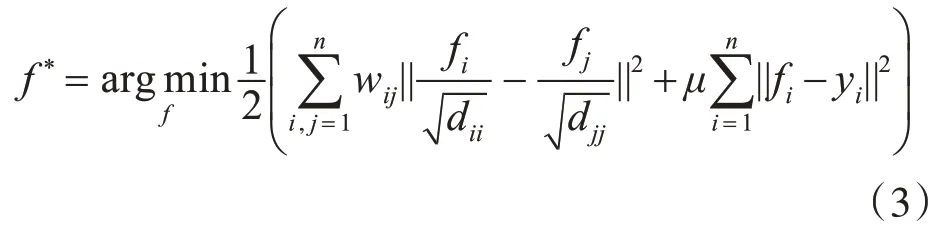
其中μ用于平衡光滑项（第一项）和约束项（第二项），fi表示节点i相对于查询对象的排序值。由文献［10］可知流形排序函数可转化为

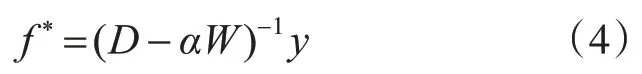
6）假设图像边界为背景，将图像边界节点设为查询节点并通过式（4）计算排序值。以上边界为例，根据式（4）计算出排序值ft*。并利用查询节点的排序结果由式（5）计算上边界显著图：

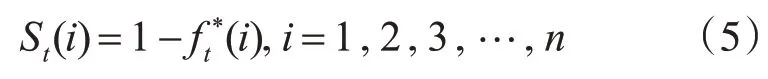
同理，计算下、左、右边界的超像素作为背景种子的显著图Sd、Sl、Sr，利用式（6）线性融合得到边界显著图，如图2（f）所示。

图2 边界先验

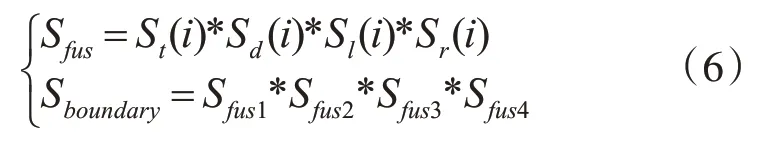
其中，i=1，2，…，N，Sfus1、Sfus2、Sfus3、Sfus4表示超像素数目为100、150、200、250时的显著图。

2.2 背景先验

文献［9］计算的显著图中背景噪声得不到很好的抑制。基于此，本节的背景先验主要步骤如下。

1）利用已有的K 个超像素，计算平均颜色和空间位置分别用表示，其中k（k=1，2，…，K）为每个超像素的标签。根据PB［11］（式（7））计算出图像边界：

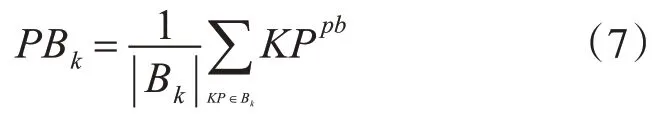
2）通过边界信息计算超像素权重，使用OTSU［12］剔除前景区域，将边界中剩余的超像素作为背景种子。通过空间信息和颜色信息得到背景种子的超像素k的显著值：

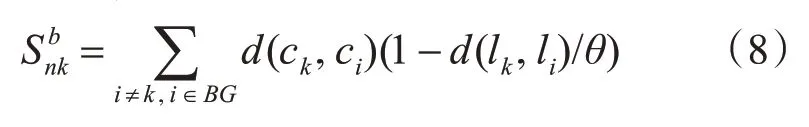
其中，n为分割的超像素数目，BG为背景种子集，li表示第i 个超像素的中心位置，ci表示CIELab 平均颜色向量，d(ck，ci)和d(lk，li)分别表示第k个超像素和第i 个超像素之间的颜色距离和空间距离。分别计算超像素数目为100、150、200、250 背景显著图，得到融合后的背景显著图，如图3（f）所示：

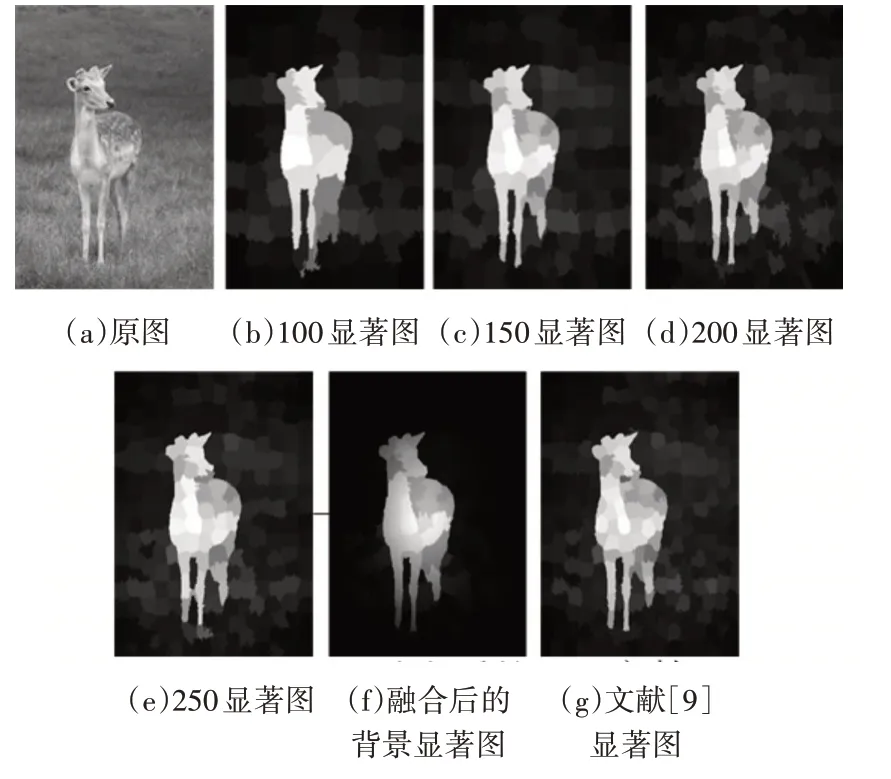
图3 背景显著图

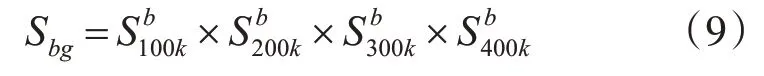
3）通过文献［13］的算法（式（10））计算超像素数目为100 的元胞自动机显著图，同理，可分别计算超像素数目为150、200、250 的显著图其中wk，i和sk，i分别利用式（11）和式（12）计算：

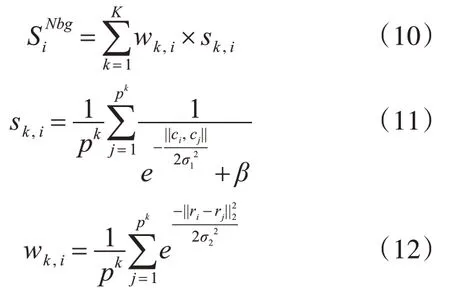
其中，N表示的当前超像素的数目，K表示将图像边缘分成K（K=3）类，属于第k 类的超像素总数为pk(k=1，2，…，K)，wk，i代表空间信息，sk，i代表颜色信息。式（11）中||ci，cj||是超像素i和超像素j在CIELab 颜色空间的欧式距离，且σ1和β是权重参数，分别取值为0.3 和10［13］。式（12）中ri和rj是超像素点i和j的坐标，且σ2是权重参数，σ2取值为1.3［13］。利用式（13）线性融合得到融合后的显著图，如图4（f）所示。

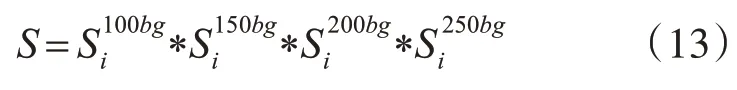
图4 元胞自动机显著图

4）将背景显著图Sbg和元胞自动机显著图进行线性融合，得到最终背景先验，如图5（d）所示。

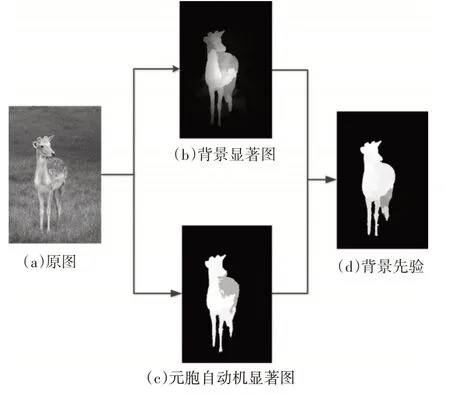
图5 背景先验

2.3 颜色先验

通过大量实验发现，暖色调和图像中其他颜色相比更具显著性［14］。参考文献［15］，将图像从RGB颜色空间归一化到r-g 颜色空间，这样有助于去除光照和阴影对显著图的影响，超像素Pk颜色显著值计算公式为

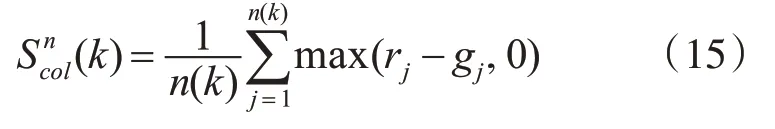
其中，k为每个超像素对应的标签，n为当前分割的超像素数目，n(k) 表示在超像素Pk总共含有n(k)个像素。rj和gj分别表示超像素Pk中第j个像素的R和G的归一化结果，分别表示为

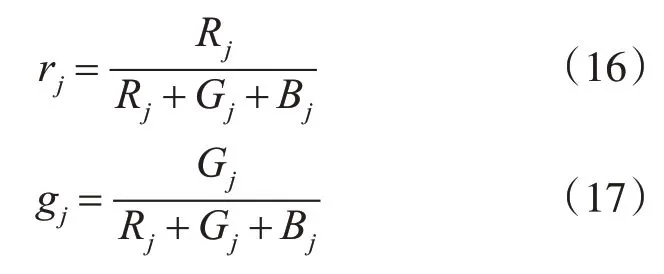
其中Rj、Gj和Bj分别是超像素Pk中第j个像素的R、G、B的值。利用式（15）分别计算超像素数目为100、150、200、250 的显著图(k)、(k)、(k)、(k)，通过式（18）计算出最终颜色先验，如图6（f）所示：

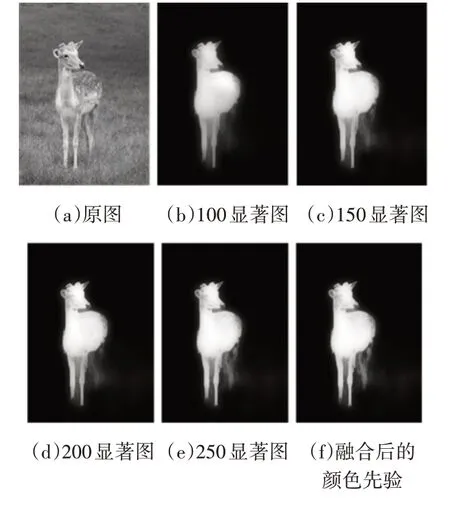
图6 颜色先验

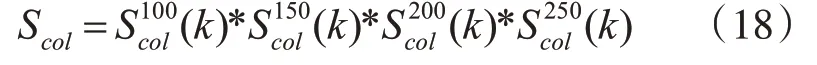
2.4 先验图融合

为了突出显著区域，本文利用多元胞自动机［13］对先验图进行融合。在该算法中，使用超像素代替元胞，用显著值代表元胞状态。利用OTSU［12］剔除背景区域。当超像素i属于前景时，相邻超像素j为前景的概率为λ=P(ηj=+1|i∈F)；当超像素i 属于背景时，相邻超像素j为背景的概率为μ=P(ηj=-1|i∈B)，其中λ和μ均为常量。后验概率可以表示为

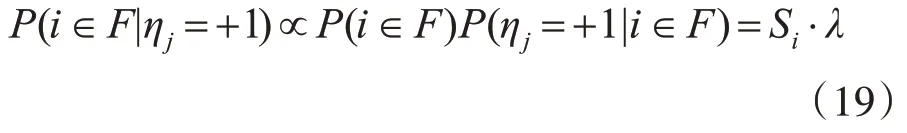
先验概率的比例Λ(i∈F)则定义为

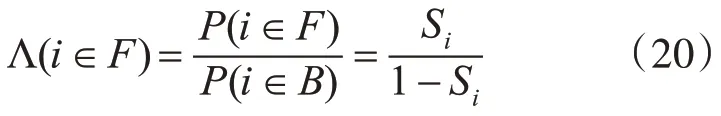
后验概率的比例为

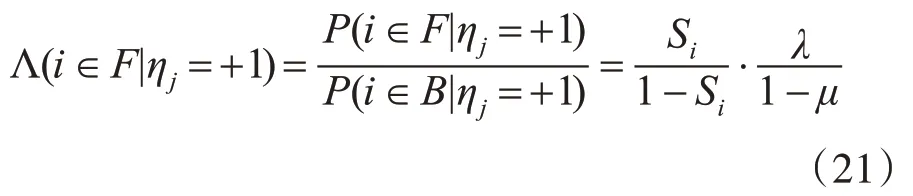
通过文献［13］的推导可知，后验概率的比例生成表达式为

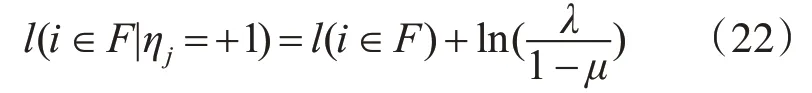
更新先验概率和后验概率的比例计算公式分别为

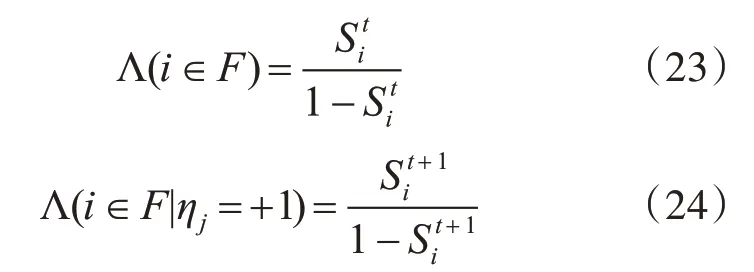
并利用同步更新原则［13］对三个先验图进行同步更新，得到最终显著结果，计算公式（25）如下：

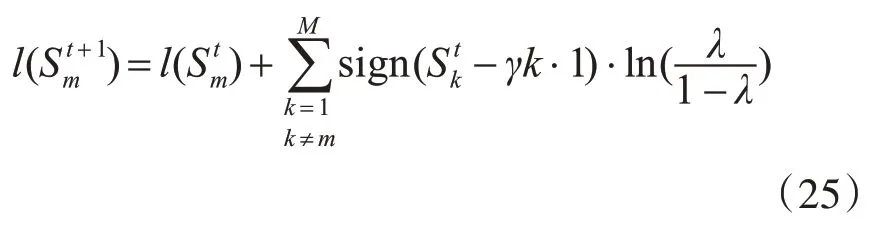
在实验过程中，令式（25）中参数γ大于0.5，且ln(λ/(1-λ))=0.15，在N2个时间步长之后，最终的显著图为SN2：

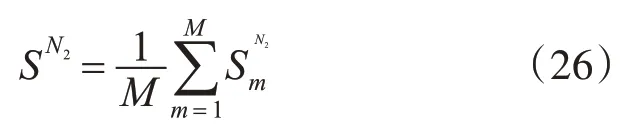
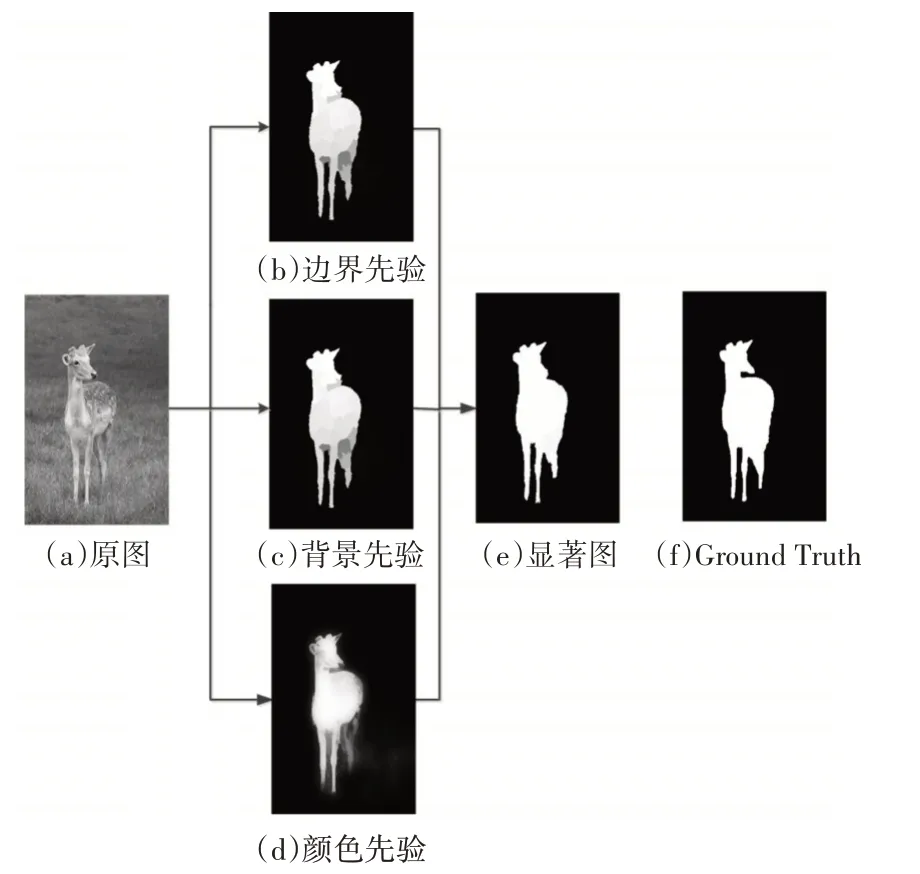
图7 融合后的显著图

3 实验与结果分析

为了评价本文算法，将本文算法与PCA［16］、AC［6］、SR［4］、LMLC［8］、GS［17］、FT［18］、BFS［19］、SF［20］、MR［10］、BSCA［13］、BL［21］、BM［22］在公开数据集MSRA1000、ECSSD和DUT-OMRON上进行比较。

3.1 运行时间

本文算法的运行时间为平均每幅图1.417s，与BL算法相比，本文算法的运行时间还是略快。

表1 在数据集MSRA1000上的平均运行时间对比表

3.2 客观评价

3.2.1 在MSRA1000数据集上的实验结果对比

通过对P-R 曲线可发现本文算法高于BM、MR、BFS 等算法，且准确率要优于BSCA、GS 算法。由图9 可以看出本文算法的准确率和F-measure值都明显高于其他算法，与BFS、LMLC、PCA、BM 算法相比，本文算法的准确率，召回率和综合指标F-measure值均有明显的提升。通过这三项指标发现，在MSRA1000 中，本文算法稳定性更高，鲁棒性较好。

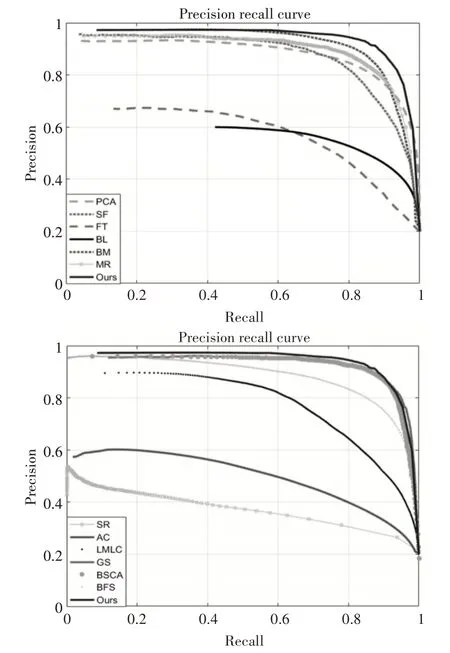
图8 P-R曲线的比较

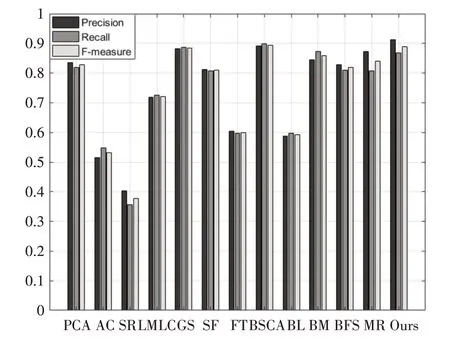
图9 仿真评价指标柱状图

3.2.2 在ECSSD数据集上的实验结果对比

本文算法的P-R 曲线与BSCA 算法相近。与BFS 算法和MR 算法相比，本文算法的准确率和召回率要略胜一筹。与其他算法相比，本文算法的精确度有明显提升。通过图11 看到本文算法在背景复杂的情况下，准确率要略高于BSCA、MR、GS 算法。而综合评价指标F-Measure 要高于BSCA、MR，GS等算法。

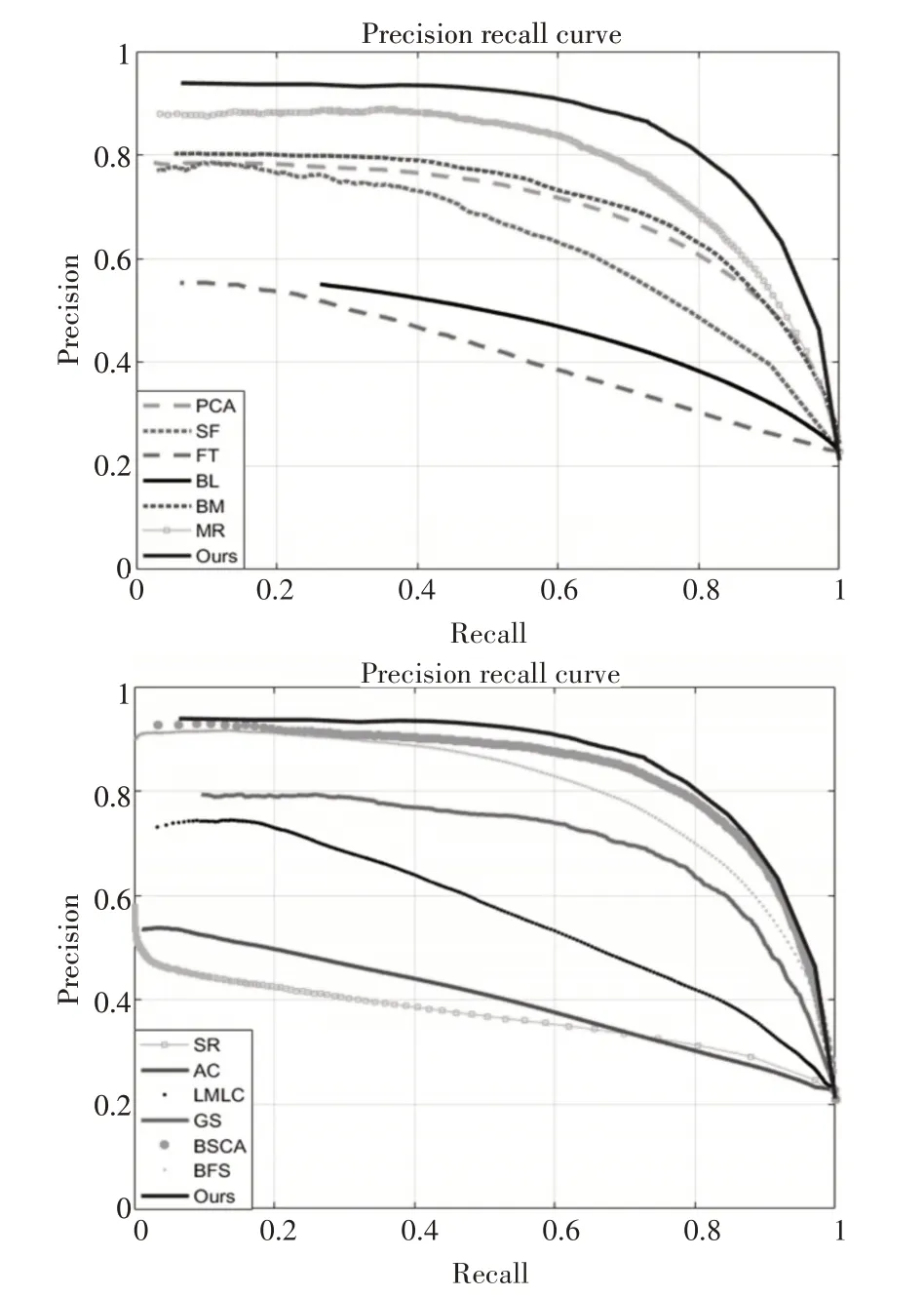
图10 P-R曲线的比较

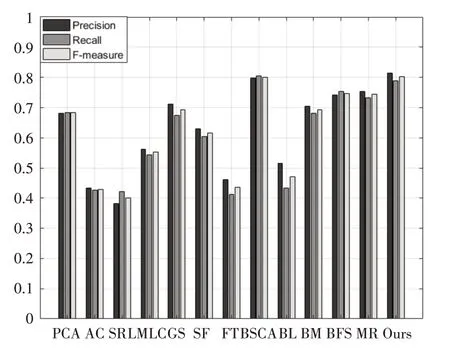
图11 仿真评价指标柱状图

3.2.3 在DUT-OMRON数据集上的实验结果对比

通过P-R曲线可以发现本文算法与BL算法相近，但是准确率明显高于BL 算法。与其他算法相比，本文算法的准确率和召回率都有明显提升。从图13 可以看出，本文算法的准确率、召回率和F-Measure 均高于BL 算法。与BSCA、MR 和GS 这三种算法相比，本文算法的准确率-召回率明显优于这三个算法。与其他算法相比，本文算法的准确率、召回率和F-Measure 均有明显提升，且本文算法波动幅度不大，较为稳定。

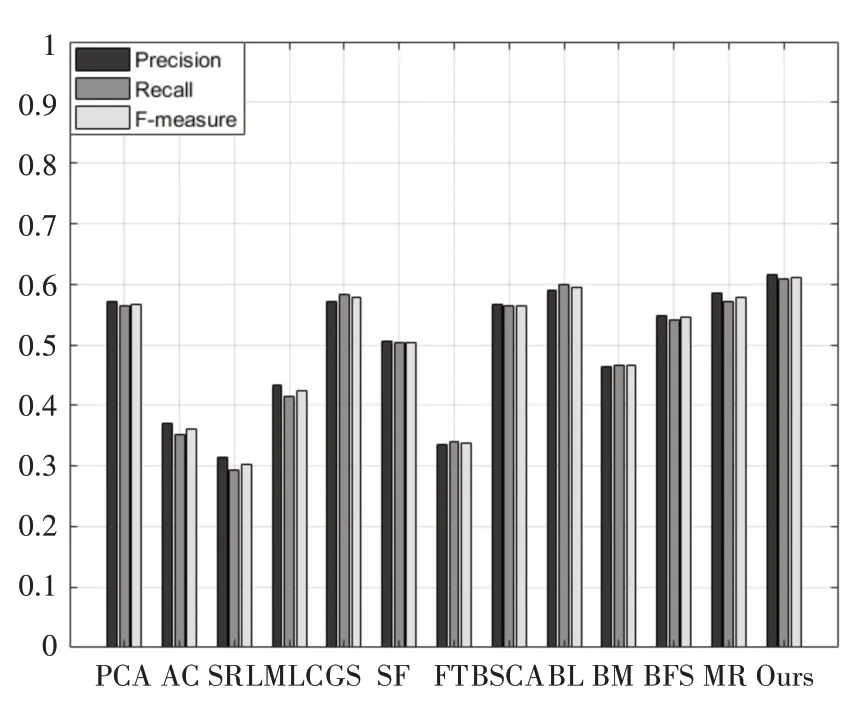
图13 仿真评价指标柱状图

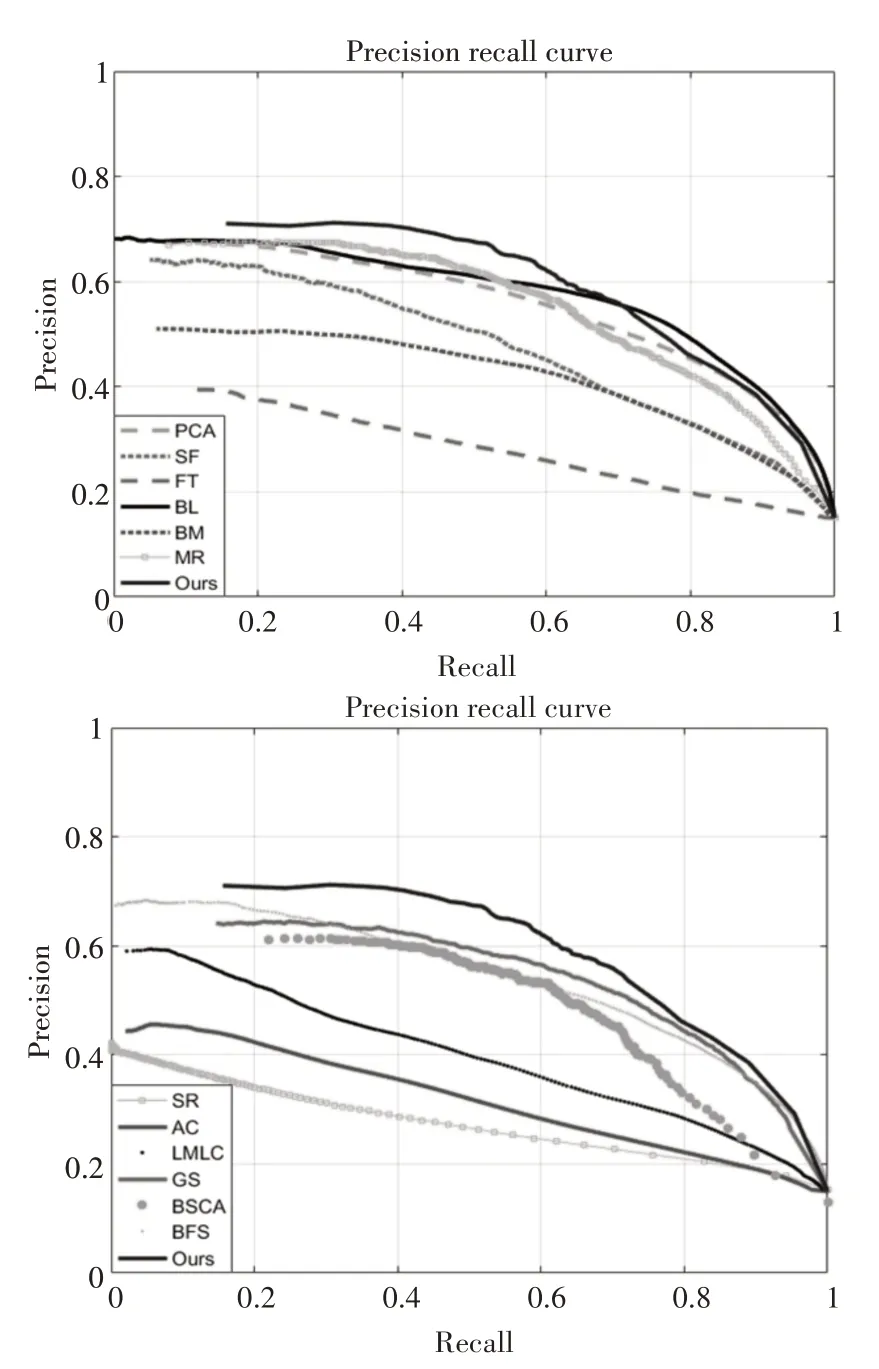
图12 P-R曲线的比较

3.3 主观评价

通过图14 可以发现，本文算法的显著区域很完整，背景噪声较少，轮廓更加清晰。与本文效果图最为接近的是MR 算法，但是对于第五张和第六张图片而言，MR 算法的检测结果中包含些许背景区域。与BFS、BSCA、BM 等算法相比，本文算法得到的显著区域更加平滑，显著图轮廓更加完整。本文算法在面对复杂背景时，处理效果有明显提升，且对背景噪声的抑制也得到了加强，检测结果更加精确。

图14 12种算法的显著图对比

4 结语

本文提出的多先验融合的显著性检测算法，利用先验知识（边界先验，背景先验和颜色先验）计算出先验图，在融合时采用多元胞自动机计算模型进行融合，生成最终高质量的显著图。通过与其他算法比对，本文显著图的结果有明显的改进，可以突出显著区域，而且可以很好地抑制背景区域。在公开数据集MSRA1000、ECSSD 和DUT-OMRON 上进行实验，与其他方法相比，准确率、召回率和F-measure值都得到很好的提升。但是当遇到目标物体内部较为复杂的场景时，本文还不能准确检测其中的显著区域。下一阶段的研究目标是如何更好地提高复杂场景下图像的显著性检测效果。