基于Z-score 模型的学员分组答辩成绩组间差消除办法*

杨小军 冯 斌 柏志尧 董 方

（1.国防大学联合勤务学院后勤与装备信息资源教研室 北京 100858）（2.国防大学联合勤务学院教学考评中心 北京 100858）

1 引言

答辩是一种常用的考核方法，通常将答辩成绩和笔试成绩两者结合，将两部分成绩各赋以一定的权重，用计算得出的综合成绩来作为考核人员的最终成绩。由于答辩需要被考核人员按顺序依次进行，如果只安排一组进行答辩，会导致时间成本较高。因此，在实际组织答辩时，都是抽签将学员分成几组，几组同时进行答辩。作为主导答辩的老师，都会力求客观公正地评价每名学员的成绩。各组的老师在学员答辩时，都是严格按照相同的标准评判学员的成绩，因此，同一组内的学员成绩可以做到公平公正。但由于每名老师的主观评价标准不一样，比如A 组的某老师将优秀的标准定为95分，B组的某老师则将优秀的标准定为85分。这样一来一名优秀的学员选择到A 组或是B 组答辩时，最终得到的答辩成绩是不一样的。我们将这种由于各组评委老师主观评价标准的差异而导致的学员成绩差异，称之为组间差。

组间差导致了学员考核时的不公平，对于这种现象，一种常用的解决方案就是各组间统一评分标准。同时采用抽签的方式，哪个学员进入哪个考场由自己抽签决定，尽最大可能消除学员对评价不公正的抱怨。但统一评分标准的实施取决于评委老师的主观意志，不好实现，抽签方式也没有从本质上消除组间差，需要一种更好的消除组间差的方法。下面我们从算法层面讨论如何彻底消除组间差。

2 组间差消除算法

学员的答辩成绩是一组单指标的数值型数据，对数值型数据进行度量的指标有两个：一是分布的集中趋势，反映各数据向数据总体中心值靠拢或聚集的程度。二是分布的离散趋势，反映各数据远离数据总体中心值的程度。学员答辩成绩存在组间差的原因是每组评委的主观评价标准不一致，反映到数据层面就是各组成绩的集中趋势和离散程度不一致。对一组数值型数据来说，其集中程度用平均数来度量，其离散趋势用标准差或者方差来进行度量［2］。消除组间差的方法就是将各组数据同时进行标准化变换，具体方法是将各组数据同时减去平均分，并除以标准差。这种方法称为Z-score 标准化方法，计算公式如下［1］：

其中，v为学员的原始分数，μi为i 组学员成绩的均值，σi为i 组学员成绩的标准差，v′为标准化后的学员成绩。公式中采用标准差去度量数据的离散程度，而不采用方差，就是为了计算时保持与平均值同一量纲。采用式（1）经过标准化变换之后的各组分数平均数都为0，标准差都为1。这样一来，各组成绩的集中程度和离散趋势就一致了，达到了消除各组成绩组间差的目的。

采用式（1）进行标准化变换之后的成绩虽然消除了各组成绩之间的组间差，但是各组学员成绩的平均值都是0，围绕0 上下波动。学员辛苦学习了一年，最后得到的成绩是0 分甚至是负分，这是很不合理的。因此我们需要将第一次标准化后的成绩再变换一下，将成绩再乘以总体学员成绩的标准差，加上总体学员成绩的平均值，其变换公式如下：

式（2）中，v″为标准化变换后的学员最终成绩，v′是学员第一次标准化变换后的成绩，公式中的σ是总体学员成绩的标准差，而不是各组的标准差，μ是总体学员成绩的平均值，不是各组的平均值。经过如此一变换，学员的成绩就回到了合理的范围之内，且所有学员成绩的标准差和均值都一致了。

3 算法验证实验

下面我们以学院2019 年度某班次学员毕业设计答辩为例来对算法进行验证。该班次学员学制1 年，全班共有42 名学员，答辩分3 个组同时进行，每一组14 名学员，学员的组别和答辩次序在答辩开始前通过程序随机生成，因此理论上各组之间优秀学员的比率相差不大。每组安排7 名评委老师，学员的原始答辩成绩为各评委评分成绩相加，先减去一个最高分，再减去一个最低分，然后除以评分人数减2。学员原始答辩成绩由式（3）计算后得出，yi为某评委为答辩学员打分成绩，Y为当前答辩学员的得分集合。

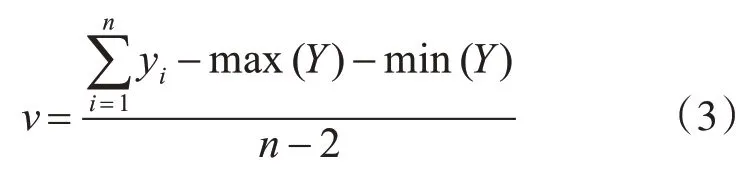
表1 为学员分组情况和通过式（3）算出的原始答辩成绩。为保护学员的隐私，我们将学员的真实姓名隐去，分别以学员1、学员2……代替。

表1 2019年度XX班次学员毕业设计原始答辩成绩表

计算得出，1 组学员的平均成绩μ1为88.34，标准差σ1为5.79。2组学员的平均成绩μ2为90.2，标准差σ2为4.98。3 组学员的平均成绩μ3为89.87，标准差σ3为5.63。全体42 名学员总的平均成绩为89.47，标准差为5.4。从学员的原始答辩成绩我们基本可以看出，第1 组学员的平均成绩最低，成绩之间的标准差最大，代表学员水平之间的差异最大，学员平均成绩低有两个可能，第一是该组学员的水平确实很低，另外一种可能是该组答辩老师的评判标准过于严苛，下面通过对原始答辩成绩进行标准化变换来验证这两种可能性。通过式（1）对学员的答辩成绩进行标准化变换后，得到的成绩如表2所示。通过式（2）对表2的成绩再一次进行转换，最后得到的学员标准成绩如表3所示。

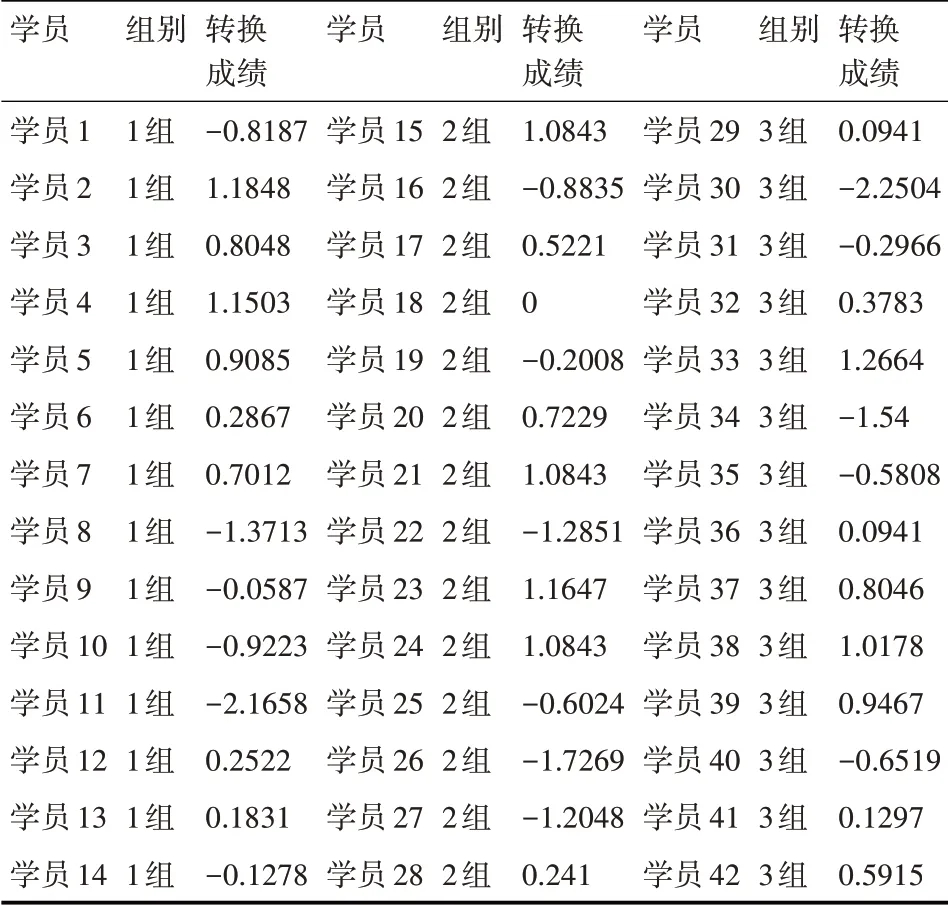
表2 第一次转换后的成绩

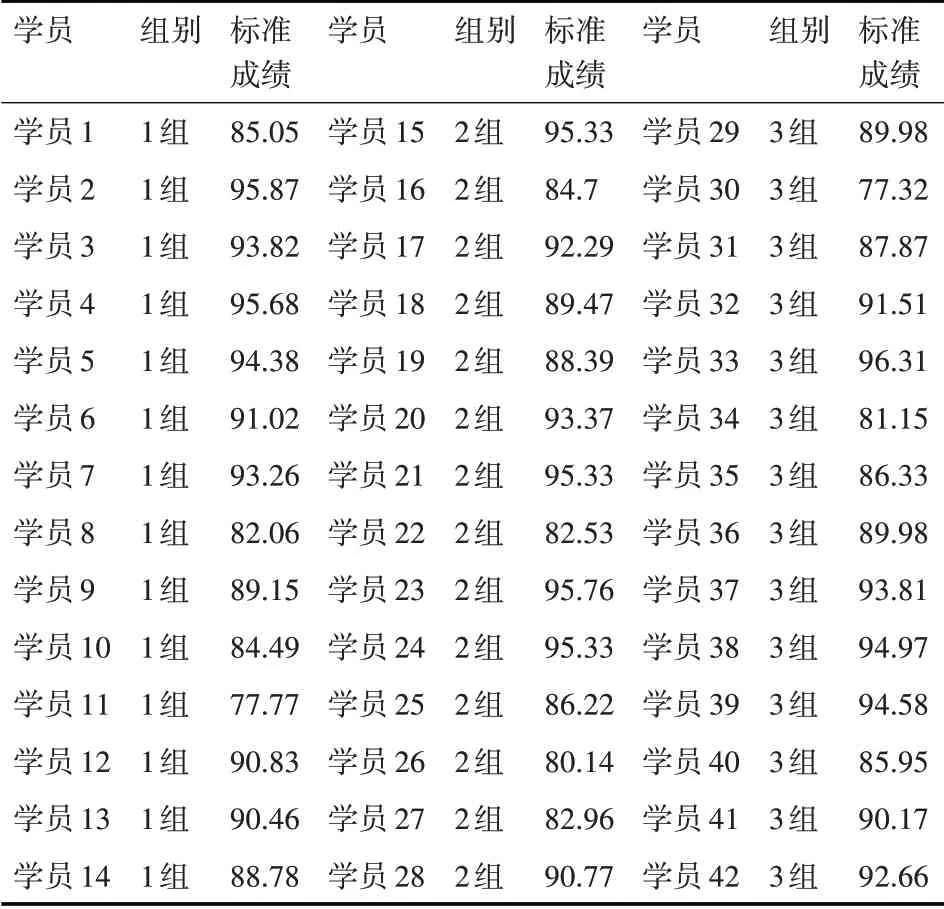
表3 2019年度XX班次学员毕业设计标准成绩表

为了说明经过标准化处理之后的成绩比原始答辩成绩更为合理，我们将这两份成绩分别与专业理论考试成绩进行比较，因为专业理论考试成绩是笔试成绩，相比答辩成绩更为客观，专业理论考试成绩如表4 所示。我们分别计算原始答辩成绩与专业理论考试成绩的相关度，以及标准化后的答辩成绩与专业理论考试成绩的相关度，将两个相关度进行比较。以专业理论考试成绩为准绳，谁与其相关度更大，谁就更合理。

表4 2019年度XX班次学员专业理论考试成绩表

通过计算，得出标准化后的答辩成绩与专业理论考试成绩的相关度为0.9611，原始答辩成绩与专业理论考试成绩的相关度为0.9541，两者都是高度相关且非常接近。但标准化后的答辩成绩与专业理论考试成绩的相关度更高，说明经过标准化后的答辩成绩更为合理。至于两者数值非常接近的原因有两个，首先，样本数据量不足，学员只有42 个，分成3 组。其次，为了尽量保持客观公正，事先制定了统一的答辩评分标准并召集全体评委开会，要求3 组评委按评分标准统一执行，最大限度地保证了原始答辩成绩的客观公正。

将表1 中的原始答辩成绩按成绩由高到低排序，取前10 名，得到表5。将表3 中的经过标准化处理后的成绩由高到低排序，取前10名，得到表6。

表5 学员毕业设计原始答辩成绩前10名情况

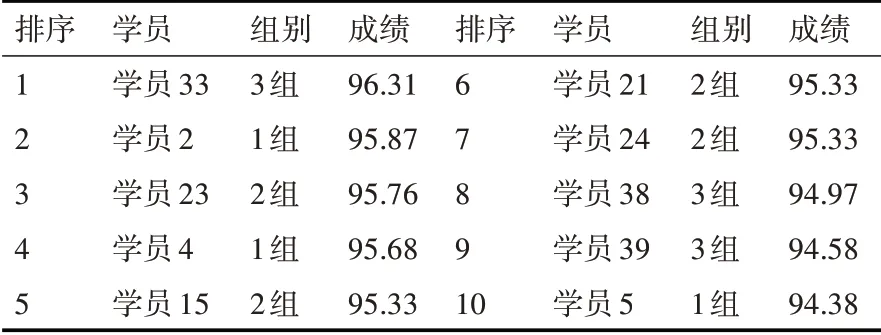
表6 学员毕业设计标准化答辩成绩前10名情况

通过比较表5和表6，不难发现如下几个规律：首先，两个表中学员的重合率高达80%，也就是说对两种成绩分别取前10 名，有8 名学员是重合的，这符合客观规律，因为优秀的学员不管怎么排序，始终是优秀的，如学员33 在两种排名中都是处于第一名的位置；第二，虽然两个表的学员重合率高达80%，但排名会发生变化。其中第1 组的学员排名变化最大，在原始的答辩成绩排名中，第1 组学员只有2 人进入前10 名，且排名相对靠后，分别为学员2，排名第7，学员4，排名第9。经过标准化处理后，学员2 由第7 名上升到了第2 名，学员4 由第9名上升到了第4名，并且第1组的学员5原来在10名之外，成绩经过标准化处理之后，上升为第10名。这说明与其它两组评委相比，第1 组的评委老师评分标准过于严苛。另外经过标准化处理后，第3 组的学员37 退出了前10 名，第38 名和第39 名的名次都后退了1 至2 个名次，说明第3 组的评判相对较为宽松。第2组的4名学员在两个表中都进入了前10，说明该组的评判最为公正，这4 名学员在表6中的排名较表5退后了1到2位，说明该组的评判较第1 组宽松；第三，在表5 和表6 中，第2 组的4位学员的成绩都出现了很大的重合，没有拉开名次之间的差别，这一点我们在计算答辩成绩的标准差时就可看出，第二组答辩成绩的标准差σ2为4.98，是3 组中最小的，这说明该组成绩的离散程度最小，评委老师没有充分将成绩距离拉开。

4 结语

答辩是常用的一种考核方式，在院校和企事业单位都用得很多，当参加面试的人数过多时，通常采用分组答辩的方式进行。为了公平起见，答辩主办方一般会采用抽签，各组间统一评分标准等方法来尽量消除各组评分之间的差异。但由于如何执行评分标准取决于评委的阅历和知识背景等因素，主观性较强，因此无法完全消除各组评分之间的组间差，所以必须引入算法才能消除各组评分的组间差，实现完全的公平公正。本文引入Z-Score 数据处理标准化方法并对其进行了改进，将各组原始答辩成绩经过两次标准化变换后，最终去除了各组成绩之间的组间差。该方法消除了分组答辩中由于各组评委主观评分标准不一致而出现的答辩成绩组间差，且操作简单，在学员的考核、面试、招生等活动中具有现实意义。