农业类大数据分类预测算法研究*

叶 煜 李 敏 文 燕

（成都农业科技职业学院信息技术分院 成都 611130）

1 引言

我国是一个传统农业大国。随着科技的发展，我国农业进入了一个新时期。一系列的农业生产、管理和经营，产生大量的农业数据。农业从业者与农业相关部门需要各种有意义的农业信息指导农业决策。如何很好地利用这些数据，引导农业生产、管理和经营，需要对数据进行深度分析。数据分类是大数据分析的关键内容。这些农业数据往往带有大量不确定性的、不完整的、有噪声的以及冗杂的信息［1］，从这些冗杂的数据信息中发现有价值的信息，找到它们的内在规律，建立能尽可能反映事物实际特征的模型，使数据分类更易与先验知识融合以适应大数据处理要求，是近年来数据分类预测算法研究的热点。目前，基于神经网络的分类算法应用于对农业数据进行自动分类是一个行之有效的方法。例如，BP 神经网络、支持向量机、广义神经网络等［2~10］。但神经网络往往存在收敛速度慢、训练时间长、对冗杂的农业数据分类精度低等问题［11~12］。因此，找到一种训练时间短、快速且准确获得最优解的分类算法是研究的重点。本文在分析了极限学习机及遗传算法基础之上提出了基于遗传算法的极限学习机，能较好地提高数据分类精度且具有良好的泛化性能。

2 极限学习机

极限学习机（Extreme Learning Machine，ELM）是一类基于前馈神经网络构建的机器学习系统或方法［13］。在训练阶段，与单隐层前馈神经网络基于梯度算法不同的是，极限学习机采用随机或人为设定输入层权重和偏差，之后不需要更新，学习过程仅计算输出权重。当所有节点都得到相应的权重和偏差，就完成极限学习机的训练。单隐层前馈神经网络由输入层、隐含层和输出层组成，如图1 所示：

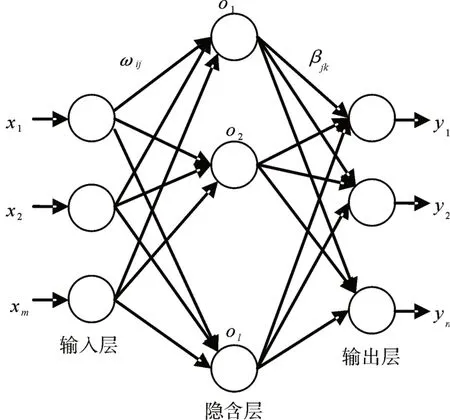
图1 单隐层前馈神经网络

对于单隐层神经网络，ELM可以随机初始化输入权重和偏差并得到相应的输出权重。假设单隐层神经网络有N 个任意的样本｛Xi，ti|Xi=［xi1，xi2，…，xin］T∈Rn，ti=［ti1，ti2，…，tim］T∈Rm｝。若隐含层有n 个节点，激活函数为g（x），输入权重Wi=［wi，1，wi，2，…，wi，n］T，输出权重βi，设bi为第i 个隐层单元的偏置。那么有l个隐层节点的单隐层神经网络可以表示为

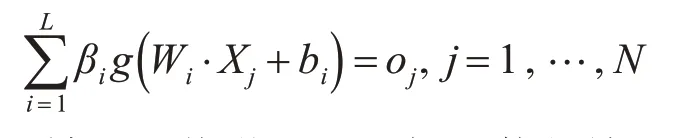
单隐层神经网络学习的目标是使得输出的误差最小，则存在βi，Wi和bi，使得

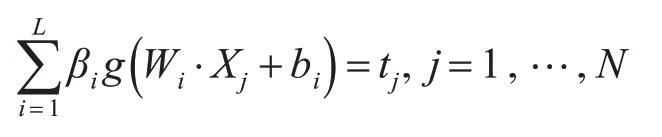
隐层节点的输出为H：

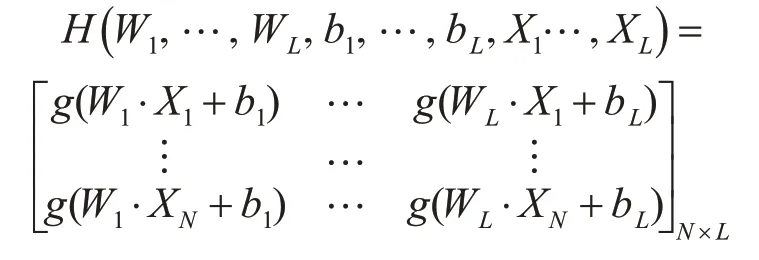
隐层1个节点与输出层之的输出权重为β：

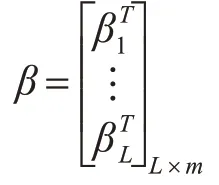
训练集的目标矩阵T：

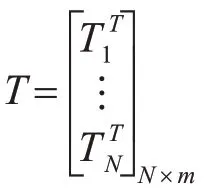
上述可以矩阵表示为Hβ=T。ELM 算法的输入权重Wi和隐层偏差bi确定了，隐层的输出矩阵H也就唯一确定。训练单隐层神经网络可以转化为求解一个线性系统Hβ=T。于是输出权重β可以被确定：β̂=H+T（H+是矩阵H 的Moore-Penrose 广义逆）。

3 遗传算法

遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种基于“适者生存”的高度并行、随机和自适应的优化算法，通过复制、交叉、变异将问题解编码表示的“染色体”群一代一代不断进化，最终收敛到最适应的群体，从而求得问题最优解的方法［14~15］。遗传算法的工作过程如下：

1）初始化。首先随机生成一组可行解，即第一代染色体。

2）适应度函数。然后适应度函数计算每一条染色体的适应程度，根据适应程度进一步计算每一条染色体在下一次进化中选中的概率。

3）遗传算子。遗传算法有三类遗传算子：选择、交叉、变异。选择算子负责选择出交叉时所要使用的父母染色体，将它们传到下一代群体中。常用选择算子有轮盘选择、锦标赛选择和排名选择。交叉算子对两个相互配对的染色体依据交叉概率按某种方式相互交换其部分基因，从而形成两个新的个体。基本的遗传算法采用单点交叉。变异算子模仿自然界变异现象，依据变异概率改变个体编码串中的某些基因值，从而形成一个新的个体，以保持个体多样性。

遗传算法工作流程图如图2。

图2 遗传算法工作流程

4 极限学习机的优化

极限学习机（ELM）随机生成输入层权值和隐含层阈值，致使网络不稳定。为提高极限学习机在农业数据上的分类精度，利用遗传算法（GA）对极限学习机进行优化，将遗传算法的全局最优搜索能力和极限学习机的强学习能力结合起来。算法将极限学习机输入层权值和隐含层阈值映射为遗传算法种群中每个染色体上的基因，染色体适应度对应于极限学习机的分类精度。在遗传算法每次迭代过程中，从通过了选择、交叉、变异的子代种群里，选择最优染色体从而获得优化的极限学习机输入权值和阈值。提高网络稳定性，降低分类的误差。

基于遗传算法的极限学习机（GA-ELM）工作过程如下：

1）种群初始化。设输入层的神经元m，隐含层的神经元n，初始化种群为X，染色体数量为N，每个染色体xi，都包括m.n 个输入权值和n 个阈值。初代种群可以表示为

其中，aij为输入层权值；bhk为隐含层阈值。

2）适应度函数。利用极限学习机对学习样本的分类预测输出误差作为适应度函数，计算初代种群中个体的适应度参数。

3）选择染色体。在对初代种群进行选择、交叉、变异等操作之后，选择适应度大的个体形成新和种群。循环往复、依次迭代，每进化一次，计算适应度，保留适应度最好的染色体，当达到预先设定的遗传代数，选择出适应度最高的染色体，并以此作为极限机最优输入权值和隐层阈值，从而获得最佳网络结构。

5 结语

算法采用UCI 中的Iris 和Wine 数据集进行测试，选择的Iris 数据集包含4 个特征，3 个类别，150个样本，Wine 数据集包含13 个特征，3 个类别，178个样本。遗传算法进化迭代次数设为50，交叉概率0.4，变异概率0.1，种群规模为40。经过10 次测试取平均值，ELM 在Iris 数据集上的分类精度为93.43%；GA-ELM 在Iris 数据集上的分类精度为95.62%；ELM 在Wine 数据集上的分类精度为60.15%；GA-ELM 在Wine 数据集上的分类精度为81.38%。可以看到，基于遗传算法的极限学习机在样本特征较少时分类精度提升较小，但在样本特征较多时，分类精度提高幅度很大，非常适合于特征点较多的农业类数据的分类预测。基于遗传算法的极限学习机可以很好地提高农业数据分类性能，有利于促进农业信息化的发展。