基于改进BP-LMS 自适应滤波器算法的仿真研究*

解本巨 王 宁

（青岛科技大学信息学院 青岛 266100）

1 引言

自适应滤波器是以线性维纳滤波和Kalman 滤波为基础发展起来的一种新型滤波技术，由于其性能良好，在未知环境的状况下具有较强的适应能力［1］，因此在现代通信处理、信号去噪和自动化控制等方面有着广泛的应用。自滤波技术发展以来，研究者主要集中致力于复杂不确定性条件下的信号扰动，通过改进传统滤波算法模型进行参数更新。例如归一化最小均方误差NLMS 算法、迭代可变步长VSS算法、变换域LMS改进算法等。这些原理都是基于传统LMS（最小均方误差）自适应滤波器，修改算法步长μ常数改为变量控制，通过收敛和时域变化规则建立联系［2］。因此基于线性控制步长因子的方法始终不能解决自适应滤波器稳态失调量和收敛速度的矛盾［3］。

随着信息技术的发展，非线性信号处理越来越重要，传统自适应滤波器面临的问题越来越多。近年来，人工神经网络发展迅猛，其应用方面十分广泛，以多层前馈BP神经网络为例，在非线性大规模并行处理和自组织自学习能力方面引起广泛重视，并取得了很多成果。使用神经网络解决自适应滤波信号处理问题，无疑是一个好的办法。基于理论分析，本文采用附加动量-自适应学习速率改进BP神经网络的方法融合LMS自适应滤波器，建立关系模型，控制信号数据处理过程。

2 LMS自适应滤波算法

2.1 自适应滤波器原理

自适应滤波器是能够根据输入信号自动调整性能进行数字信号处理的滤波器［4］，其本质是根据环境改变通过自适应滤波算法来实现更新滤波系数和结构，从而达到滤波功能的实现。原理如图1所示。

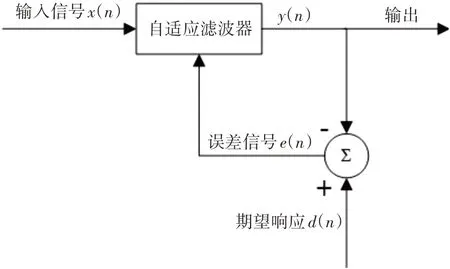
图1 自适应滤波器原理图

图中：n 为时间变量；x（n）为n 时刻的输入信号，其中包含有用信号和待滤除的噪声；y（n）为滤波器的输出信号；d（n）为已知的参考信号或期望响应；e（n）为估计误差信号，有e（n）=d（n）-y（n）。自适应滤波器是一个系数可调的FIR（有限长单位冲击响应）数字滤波器，其系数根据一定的自适应算法进行调节，调节的目标是使e（n）达到最小值。当e（n）达到最小值时，也即意味着滤波器的输出信号y（n）实现了对期望响应d（n）的最佳估计。

2.2 基本LMS算法

由Widrow 和Hoff 早些时候提出的LMS 算法，运用了最速下降法的思想，在权值系数向量随时间变化过程中加入比例项-∇，即在“上一时刻”wi与“现时刻”wi+1之间加入负均方误差梯度［5］，由此得到

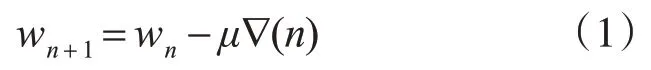
其中μ为步长因子，是决定算法稳定性和收敛快慢的常数。在计算∇n时由于计算复杂，常常采用近似值∇̂(n)=-2e(n)x(n)进行取代，所以基于常数μ 的LMS算法公式可以表示为

LMS 算法在解决线性问题时表现出比较明显的优势，但稳态失调量和收敛速度依旧是最大的矛盾，在现代信号处理中，面临的非线性问题也越来越多，使用基本LMS算法不再满足要求。本文使用附加动量-自适应学习速率法修改BP 网络权值，并结合LMS自适应滤波器构造模型，利用神经网络自学习的特点，更准确确定参数变量，改善稳态失调量和收敛速度的矛盾。

3 改进BP-LMS算法

3.1 附加动量-自适应学习速率优化

利用BP 神经网络对LMS 算法输入信号进行融合时，由于信号的相似性和广泛性，以及按照误差负梯度方向优化权值的特性，易造成BP 网络收敛性效果不佳，陷入局部最小［6］。针对传统BP 神经网络的缺陷，本文采用附加动量-自适应学习速率的方法进行改进。

使用动量因子附加作用于神经网络的反向传播过程，在每一次权值变化中，加入一项正比于前一次权值（或阈值）的变化量，产生新的权值［7］，带有附加动量因子和阈值变化的调节公式为

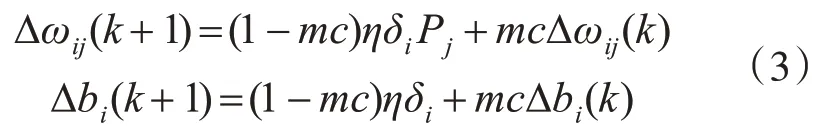
其中，k 为训练次数，mc 为动量因子，一般取值为0.95左右。在进行附加动量法训练过程中，为了防止权值修正过大或者过小，采用以下公式作为修正限制条件，判定条件为

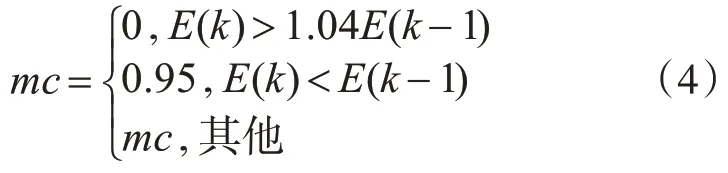
其中E（k）为第k 步误差平方和。当mc=0 时，即未加入动量因子，其误差变化如图2所示。

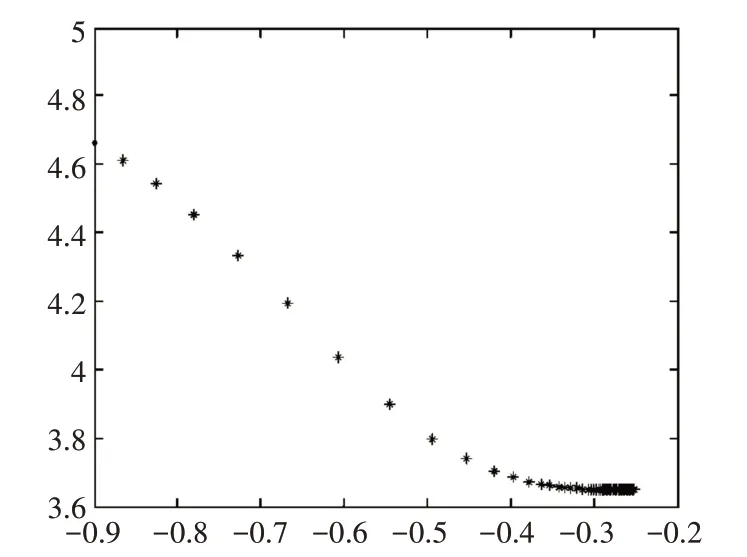
图2 mc=0的变化趋势

网络训练陷入局部最小值，停止不动。当加入动量因子并取值为0.95 时，如图3 所示，网络会在附加动量作用下，越过局部最小值。

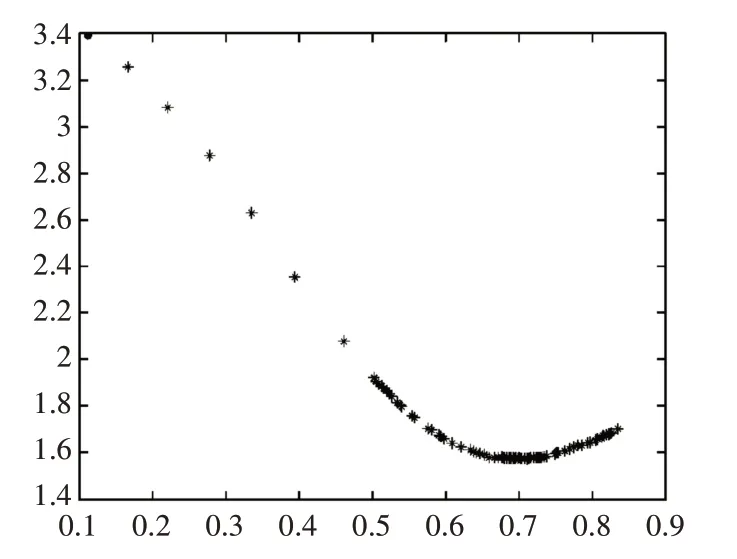
图3 mc=0.95的变化趋势

对于网络学习速度过慢的问题则采用自适应学习速率法进行控制。自适应学习速率通过检验网络权值是否降低了误差函数作为标准，如果显示降低，则表示学习速率小，可以增加一个量，如果没有，则可以适当减小［8］。自适应学习速率公式为

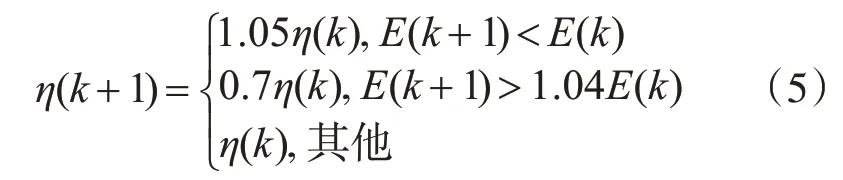
图4，图5 分别表示未加入自适应学习速率法和加入自适应学习速率法在网络训练中达到相同精度的迭代情况。

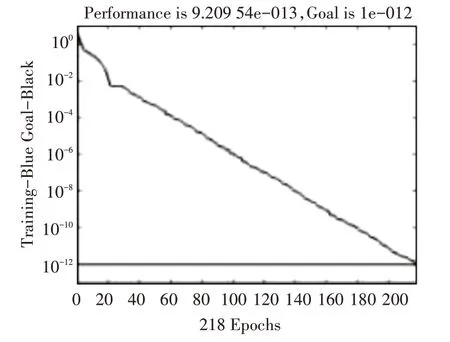
图4 网络训练误差（传统算法）

图5 网络训练误差（改进算法）

可以看出网络达到相同的误差时，未使用自适应学习速率法需要迭代218 次，而加入自适应学习速率法只需要26次，在速度上有明显改观。

附加动量法使动量因子与BP神经网络权值相结合，避免因网络权值更改过大陷入局部极小，可以找到全局最优解。自适应学习速率可以缩短网络训练时间，避免由经验判断而盲目性的学习。改进后的BP 神经网络与传统型BP 神经网络对比如图6 所示：新算法模型可以促进网络性能优化、更具有鲁棒性。结合LMS自适应滤波算法，可以更准确地学习到最优μ步长，实时加快收敛速度，提高滤波器精度。

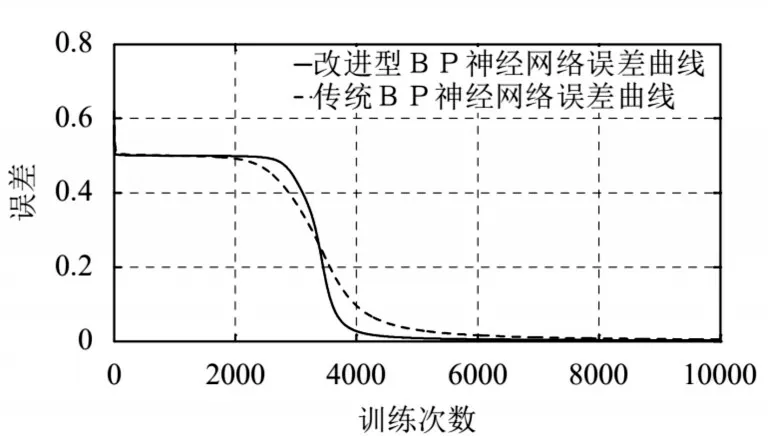
图6 传统与改进后BP神经网络对比

3.2 BP-LMS模型

使用BP 神经网络融合LMS 算法并进行优化，首先建立神经网络与自适应滤波算法的模型，并通过网络结构与输入向量、误差以及学习步长相关联［9］。图3 显示了BP-LMS 模型在自适应滤波器中的融合规则，利用BP 神经网络解决滤波信号处理问题，实现BP-LMS模型。

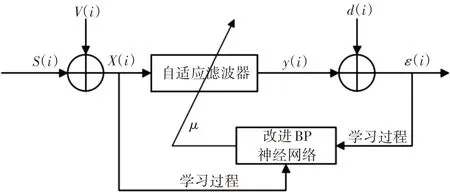
图7 BP-LMS模型自适应滤波器

其中X（i）和ε（i）为BP 神经网络的输入信息，数据以向量模式表示，μ为神经网络训练结果的输出。可以看出神经网络结合自适应滤波算法实际上就是建立学习的网络结构，通过误差和输入向量寻找最佳学习步长。学习给定样本数据，建立实时数据关联模型，并集成到BP-LMS 算法中。在网络训练结束后，通过BP神经网络算法得出的参数，代表三者之间的非线性关联。其BP-LMS 更新算法参数的规则如下：

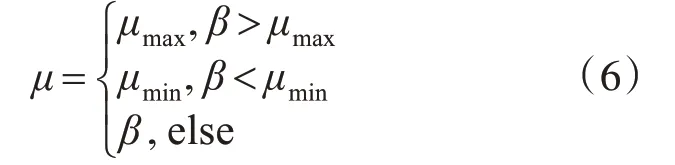
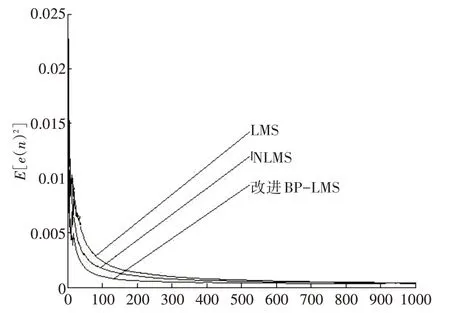
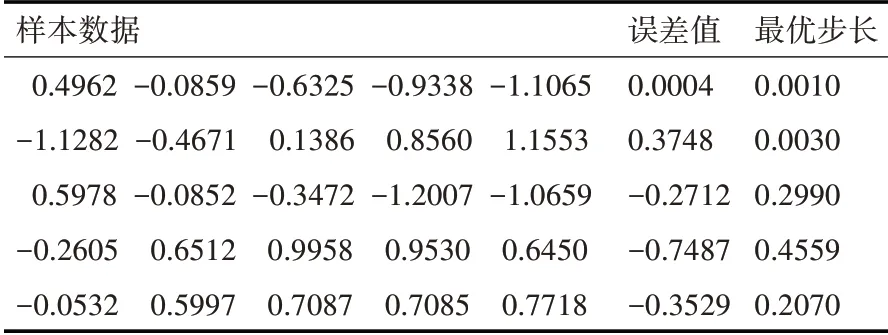
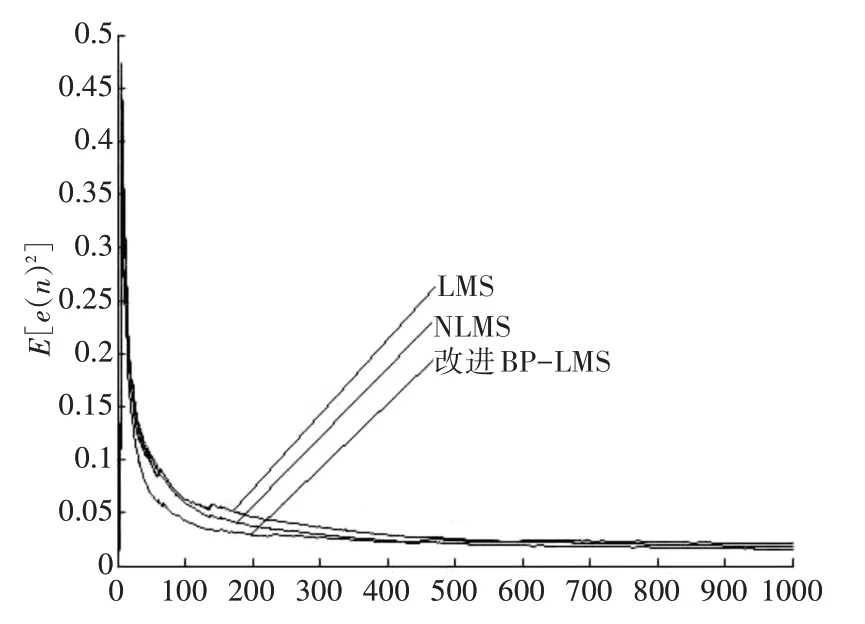
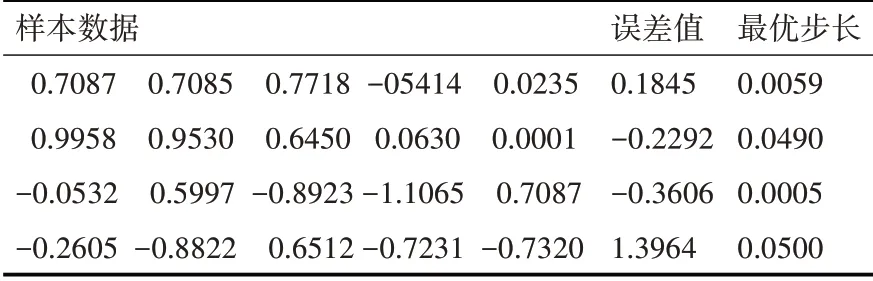
在上述方程中，β代表了在采样时间n 时刻根据输入向量X（i）和误差ε（i）得到的BP 神经网络模块的输出。为保证神经网络算法收敛性，β必须

4 实验与分析

4.1 数据采集

使用改进BP-LMS模型建立神经网络结构，首先需要采集数据作为样本集，由于大多数自适应滤波信号数据都具有相似性，故本文采用工程应用中常用的正弦波信号作为仿真数据，通过引入噪声干扰进行Matlab仿真实验和对比。

4.2 实验对比

为了验证改进BP-LMS 模型后的有效性，故与其他几种自适应算法进行仿真比较。

1）标准LMS 算法，μ步长因子是一个给定的较小的正数。

2）NLMS 算法（归一化最小均方误差），步长因子由公式μ=得出，其中η为自适应常数，δ为正数，X（i）为采样时间n时刻输入信号值。

仿真1：输入带有噪声的标准正弦波信号，和其他两种算法作性能比较，如图5所示。

图8 仿真1误差收敛曲线

仿真步骤如下：

1）滤波器阶数设定为L=10，初始权重Wi定义为0。

2）加入噪声X（i）为零均值，方差σ2为0.1 的独立高斯随机序列。

3）标 准LMS 算 法 不 变 步 长 因 子μ 设 置 为0.005。NLMS 自适应滤波器参数η和δ分别为0.15和2。

4）平均统计时间为20，样本容量为1000，在改进BP-LMS 模型中使用greed 算法寻找训练样本，部分数据如表1所示。

表1 BP模型部分训练样本数据

附加动量-自适应学习速率BP-LMS 模型最重要的是建立神经网络结构，寻找样本进行训练。根据信号数据的相似性，任意三层网络结构就可以完成随机向量的映射，所以本文采用单层BP 神经网络进行训练和预测。设定输入向量为10个单位的输出（假设自适应滤波器输出信号为8，偏差为2），隐藏层包含20 个中间单元节点。通过神经网络训练扫描模型中输出结果，产生最优步长因子μ。

可以看出，对比其他两种算法，附加动量-自适应学习速率BP-LMS 算法模型可以使得自适应滤波器在收敛速度方面取得更好效果。

仿真2：进一步评估改进BP-LMS 算法的性能和有效性，输入信号为带有噪声的高斯白噪声序列，如图9所示。

图9 仿真2误差收敛曲线

仿真步骤如下：

1）自适应滤波器阶数L=7。初始权重W（i）=［0.25，0.25，0.75，1，0.25］T。

2）输入信号s（n）为零均值方差σ2=1.5 的高斯白噪声随机序列，加入噪声X（i）为零均值，方差σ2=0.06的独立高斯随机序列。

3）标 准LMS 学 习 步 长 因 子μ 设 置 为0.005，NLMS算法两个参数η和δ分别为0.15和2。

4）平均统计时间为300，样本容量为1000。同比于仿真1，首先使用greed 算法寻找训练样本，部分数据如表2所示。

表2 改进BP模型部分训练样本数据

建立基于附加动量-自适应学习速率BP 网络模型，输入向量设定为15（假设自适应滤波器输入信号为12，偏差为3），隐藏层为25 个单元，通过神经网络再次训练。

可以看出，基于附加动量自适应学习速率BP-LMS 算法在200 次迭代周期后趋于稳定，对比于迭代周期在400 和500 次左右的LMS 和NLMS 两种算法，收敛速度上有明显的加快。

仿真1、2 实验结果可以表明，基于附加动量-自适应学习速率BP-LMS 模型具有明显的实用性。在噪声功率相同类型且已知的情况下，神经网络处理性能要比LMS 和NLMS 更有效果，在误差调整方面也更加稳定。

5 结语

自适应滤波器在通讯信号处理中具有重要的价值，随着集成电路和计算机的快速蓬勃发展，使其应用范围也在不断的扩大，已经遍及图像识别、语音信号处理和模式识别等相关领域。滤波技术发展的根本取决于算法的创新和融合，本文提出的附加动量-自适应学习速率BP-LMS 模型，采用一种新型神经网络控制技术，建立信号数据与人工神经网络之间的联系，并通过Matlab仿真实验得以证明和实现。

结果表明，通过神经网络控制信号处理过程，可以提高实时信号处理精度，更好的弥补自适应滤波器的缺陷和不足。在工程应用信号处理过程中，使用神经网络控制自适应滤波，凸显了实用性和推广性，拓宽了人工神经网络和自适应滤波结合的思想，具有重要意义和发展前景。