脉宽-调频极性捷变波形相参处理能力分析

杨志伟, 谢雪新, 李舒婉

(1. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071;2. 西安电子科技大学信息感知协同创新中心, 陕西 西安 710071)

0 引 言

波形捷变是降低雷达信号截获概率、提升抗干扰能力的有效途径。根据捷变的尺度,可分为脉内捷变、脉间捷变、脉组捷变。脉内捷变指的是波形的捷变发生在脉冲内子脉冲之间;脉间捷变指的是波形的捷变发生在相参处理间隔(coherent processing interval,CPI)内每个脉冲之间;脉组捷变指的是波形的捷变发生在CPI之间。根据回波脉冲积累的方法,波形捷变又可以分为捷变相参和捷变非相参。非相参积累实现简单,但是存在积累损失大、杂波背景下动目标检测性能恶化等问题。脉组捷变在CPI内发射的多个脉冲波形相同,通过多普勒处理,可实现相参积累,提高目标的信噪比,从而提升检测概率。脉间波形捷变时,不同波形具有不同的匹配滤波距离旁瓣,称为距离旁瓣调制(range sidelobe modulation, RSM)效应,做多普勒处理时这些距离旁瓣上的杂波能量会在多普勒域中扩散,并且无法被后续的运动目标显示(moving target indicator, MTI)处理所抵消。这些散布的杂波能量将与目标竞争,降低信杂噪比(signal clutter to noise ratio,SCNR)。脉间脉压响应的差异,相当于对每个距离单元的时域导向矢量进行了不同的幅度调制,导致杂波多普勒普展宽,空时自适应处理(space-time adaptive processing,STAP)输出SCNR损失增大,最小可检测速度(minimum detectable velocity,MDV)提高。

杂波背景下解决捷变相参问题的关键是减小脉压响应的差异性,以减轻RSM效应。文献[12-14]中提出用基于波形类型的失配滤波器(mismatch filter,MMF)来减小距离旁瓣的方法,但是该方法仅考虑了距离维旁瓣,并且这些方法仅适用于单个指定波形。文献[15-16]分别提到的正负线性调频(linear frequency modulation, LFM)信号和正负非LFM(non-LFM, NLFM)信号不同波形匹配滤波结果完全相同,是解决捷变相参的一种途径。但是其波形的个数只有两个,形式过于简单,需要寻求波形个数更多、形式更复杂的捷变波形。文献[17-20]提出了一种基于联合最小二乘MMF(joint least squares-MMF,JLS-MMF)设计的方法以部分缓解RSM效应,该方法能够在CPI内脉间多波形捷变,同时最大程度地缓解RSM效应。文献[21-22]提出了一种联合波形-MMF设计方法,使不同脉冲失配滤波后产生近似相同的旁瓣结构以缓解RSM效应,但失配滤波的解决方法以提高距离旁瓣电平为代价,并且随着波形数量的增加,性能严重下降。文献[23-24] 考虑了在每距离/多普勒小区间基础上优化的接收机滤波器,但是其代价是显著增加了计算量。文献[25-26]提出了一种针对地面动目标显示(ground moving target indicator,GMTI)雷达的改进JLS-MMF方法,该方法可以直接得到MMF系数的闭式解,而不用采用迭代的方式。文献[27]提出了一种适用于脉间波形捷变的空时自适应失配处理方法,该方法联合快时间、慢时间和空间的杂波加噪声协方差矩阵构建三维MMF以最大化输出SCNR,但三维失配滤波存在系统维数过高的问题,系统维数太高导致运算复杂度提高,同时脉间波形捷变情况下三维时空自适应失配处理无法采用后多普勒降维方法,满足独立同分布的训练样本数得不到保证。文献[28-29]提出了一种二维MMF,还基于多普勒调谐匹配滤波器设计了一种循环算法来计算二维MMF,以抑制RSM下指定距离多普勒区域上的旁瓣,然而该方法计算开销大,且需要精确的先验信息来选择指定区域。

针对脉间波形捷变存在RSM效应的问题,现有文献中大都是采用失配滤波的解决方法,且未见关于脉间波形捷变条件下目标相参积累损失、单通道MTI和空-时处理的定量性能指标分析的公开报道。本文从脉宽-调频极性脉间捷变波形具有主瓣相同、旁瓣幅度起伏小的特点出发,首先给出脉宽捷变波形的信号模型,然后推导了脉间波形捷变条件下目标相参积累、单通道MTI处理和空-时处理的性能分析模型,并给出定量性能指标。最后的仿真实验表明,该捷变波形在降低雷达信号截获概率、提升雷达抗干扰能力的前提下,能够进行相参处理,获得较好的杂波抑制性能。

1 信号模型

1.1 捷变波形信号模型

设雷达在CPI内发射个LFM矩形脉冲信号,带宽保持不变,第个脉冲的宽度为,则第个脉冲的基带信号表达式为

(1)

脉宽捷变形式有两种:脉宽滑变和脉宽跳变。设脉宽恒定时脉宽为,脉宽的变化范围为～(1-),为脉宽变化系数,=Δ=|-|表示第个脉冲的归一化脉宽变化量。脉宽滑变为相邻脉冲间脉宽间隔为=(-(1-)),可以是CPI内脉冲宽度逐渐减少，即=-(-1)(=1,2，…,),也可以是CPI内中间的脉冲宽度大、两头小,即=-|-2|,本文采用的是后一种;脉宽跳变为脉宽在～(1-)间随机取值,其脉冲宽度可表示为=-(=1,2，…,),为[0,]内的随机数。

图1给出脉间脉宽捷变和调频极性正负交替变化的发射脉冲示意图,图中PRI表示脉冲重复间隔(pulse repetition interval, PRI)。

图1 捷变波形示意图Fig.1 Diagram of agile waveform

1.2 杂波信号模型

本文的研究是在地杂波背景下开展的,在无距离模糊假设条件下,第个脉冲第个距离单元的单通道杂波信号在时域上可表示为

(2)

式中:为第个距离环的斜距;c为光速;[,]为第个脉冲第个距离单元的杂波散射响应,其表达式为

(3)

其中,为回波信号能量;为第个杂波块的散射截面积;ej为第个杂波块的散射幅度和相位;为时域角频率;为第个杂波块的方位角;为第个距离单元的俯仰角。

将单通道信号扩展可得多通道杂波信号在时域上的表达式:

(4)

式中:

(5)

其中,为空域角频率;表示第个阵元。

1.3 性能分析模型

131 模糊函数

模糊函数是评估信号的分辨率、多普勒容忍性、测量精度、抗干扰能力等的重要工具。波形()和波形()的互模糊函数定义为

(6)

当=0时,得波形()和波形()的互相关函数:

(7)

令=,得波形()的模糊函数为

(8)

当式(4)中=0时,得速度模糊函数:

(9)

可知多普勒分辨率仅与脉宽有关。

当式(4)中=0时,得距离模糊函数

(10)

自相关函数即距离模糊函数,表征回波的脉压性能,对于离散点目标和分布式目标,分别采用非周期自相关函数和周期自相关函数。互相关函数(即互模糊函数的零多普勒切面)表征雷达信号低截获和抗干扰的性能,对于分布式目标采用周期互相关函数。

将式(10)离散化,可得波形的非周期自相关函数和周期自相关函数分别为

(11)

(12)

类似地,周期互相关函数为

(13)

周期互相关函数的峰值旁瓣电平为

(14)

互相关函数的峰值旁瓣电平越高,雷达信号低截获和抗干扰的性能越差。

132 相参积累峰值增益损失

相参积累通常采用快速傅里叶变换(fast Fourier transform, FFT)的处理方法实现。设目标所在距离单元处第个脉冲的回波脉压结果为ej,则对目标的采样值可以表示为

()=ejexp(j)

(15)

式中:目标多普勒角频率=2π;=0,1,…,-1。

对应多普勒频谱为

(16)

多普勒峰值旁瓣电平(Doppler peak sidelobe level,DPSL)定义为目标所在距离单元处的多普勒频谱的最高旁瓣电平与峰值增益的比值。令,side表示距离单元处的多普勒频谱的旁瓣区域,则

峰值增益定义为目标所在距离单元处所有多普勒单元输出的最大值:

Gain=max(|()|),∈[-π,π]

(17)

峰值增益损失定义为波形捷变时目标相参积累的峰值增益Gain与恒定脉宽恒定调频时目标相参积累的峰值增益Gain的比值,即

(18)

1.3.3 单通道MTI性能

MTI滤波器通过设置适当的凹口中心来抑制不同类型的杂波,从而提高目标信号的信杂比,便于目标检测。

设第个脉冲信号经匹配滤波器后的脉压响应为

=*

(19)

式中:*表示卷积操作。

设()为距离单元处CPI内个脉冲的杂波的脉压输出,则()是距离处的杂波加上其他距离处的杂波的旁瓣响应的组合:

(20)

假设杂波具有统计独立性,即

(21)

则

(22)

定义,表示()和()的相关系数,其表达式为

(23)

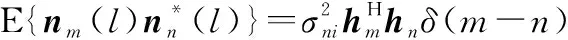
(24)

采用+1脉冲相消时,MTI滤波器的杂波输出可表示为

(25)

杂波输出的功率为

(26)

令杂波输出功率最小,则权系数可由下式算得:

(27)

式中:

=[,,…,]

(28)

(29)

(30)

将权系数代入即可求得信号输出的功率。

(1) 杂波抑制能力

杂波抑制能力用杂波衰减来衡量。杂波衰减(clutter attenuation,CA)定义为MTI滤波器输入杂波功率和输出杂波功率的比值,可表示为

(31)

(2) 输出SCNR损失

输出SCNR损失定义为捷变波形回波经MTI处理后输出SCNR与高斯白噪声情况下匹配滤波输出信噪比的比值,即

SCNR=SCNR/SNR

其中,MTI处理后输出SCNR为

(32)

设目标时域导向矢量()=[1,ej,…,ej(-1)],目标和噪声的输出功率分别为

(33)

(34)

高斯白噪声情况下匹配滤波输出信噪比SNR为

(35)

(36)

(37)

134 空-时处理性能

以全维STAP为例,利用线性约束最小方差(linearly constrained minimum variance,LCMV)准则来求解最优权矢量,其表达式如下:

(38)

式中:表示杂波加噪声的协方差矩阵;=()⊗()表示空时二维导向矢量,空间角频率=2π,空域导向矢量可表示为

()=[1,ej,…,ej(-1)]

(39)

时域角频率=2π,时域导向矢量可表示为

()=[1,ej,…,ej(-1)]

(40)

求解得最优权矢量为

(41)

脉间脉宽捷变时,根据脉压峰值增益和脉宽的关系,可以对不同脉冲脉压结果加权,使每个脉冲脉压峰值增益相同,但是距离旁瓣结构仍不尽相同,对于某一个距离单元,相当于对时域导向矢量进行了幅度调制,对于某个距离环第个杂波块用表示:

(42)

脉宽捷变下接收的杂波数据可表示为

(43)

对应的杂波加噪声协方差矩阵为

(44)

最优权矢量为

(45)

输出SCNR损失定义为脉间波形捷变情况下实际STAP处理输出SCNR与高斯白噪声情况下匹配滤波输出信噪比的比值,即:

(46)

2 仿真分析

本文所有仿真信号均为LFM信号,这里从模糊函数、峰值增益损失、单通道MTI性能和空-时处理性能4个方面对脉宽-调频极性联合捷变的LFM捷变波形的相参处理能力进行仿真分析。

2.1 模糊函数仿真

自相关函数差异定义为两个波形的各自归一化自相关函数的差值。设信号的带宽为10 MHz,采样频率为100 MHz,图2(a)给出了脉宽分别为200 μs和100 μs的两个波形的自相关函数差异,图2(b)给出了不同时宽-带宽积条件下,脉宽恒定和脉宽捷变波形的自相关函数差异的峰值与脉宽变化量的变化关系,由图中可知,相同脉宽变化量的情况下时宽-带宽积越大,自相关函数差异性越小;时宽-带宽积大于500条件下脉宽变化0.5时最大差异小于-30 dB,即脉宽-调频极性脉间捷变波形的旁瓣起伏很小。

图2 自相关函数差异Fig.2 Autocorrelation function difference

图3给出了不同时宽-带宽积条件下正负调频脉宽捷变波形的互相关函数峰值旁瓣电平与脉宽变化量的关系,由图中可知,时宽-带宽积和脉宽变化量越大,互相关函数峰值旁瓣电平越低,其近似关系为

PCCL={-10lg((1+)BT)}

(47)

图3 互相关函数峰值旁瓣电平与脉宽变化量的关系图Fig.3 Relationship between peak side lobe level of cross- correlation function and pulse width variation

2.2 峰值增益损失仿真

图4 相参积累后峰值点处多普勒剖面Fig.4 Doppler profile at the peak point after coherent accumulation

图5 相参积累峰值增益损失随脉宽变化量的关系Fig.5 Relationship between peak gain loss of coherent accumulation and the variation of pulse width

2.3 单通道MTI性能仿真

信号带宽为10 MHz,采样频率为20 MHz,CPI内脉冲数=128,目标归一化多普勒频率等于0.3。图6(a)和图6(b)分别给出了输入杂噪比(clutter to noise ratio, CNR)等于30 dB时杂波衰减和输出SCNR损失与归一化脉宽变化量的关系图;图7给出了归一化脉宽变化0.5时输出SCNR与输入CNR的关系图。由图6和图7可看出,脉冲相消数越多,杂波抑制能力越强;脉宽滑变的MTI性能比脉宽跳变好,这是由于脉宽滑变时,相邻脉冲间脉宽的变化量较小,脉压响应的差异也相应较小;时宽-带宽积越大,单通道MTI处理的杂波抑制能力越强,损失越小。

图6 单通道MTI性能与归一化脉宽变化量的关系Fig.6 Relationship between single-channel MTI performance and normalized pulse width variation

图7 输出SCNR损失与输入CNR的关系Fig.7 Relationship between output SCNR loss and input CNR

2.4 空-时处理性能仿真

仿真参数如表1所示。

表1 空-时处理仿真参数Table 1 Space-time processing simulation parameters

图8(a)给出了BT=1 000时不同捷变形式下最优空时处理和多普勒三通道联合自适应处理(three Doppler transform, 3DT)处理的输出SCNR损失对比;图8(b)给出了不同时宽-带宽积条件下脉宽滑变的输出SCNR损失对比。由图8可看出,与脉宽恒定相比,脉宽捷变情况下输出SCNR损失凹口轻微展宽,MDV变大;脉宽滑变情况下旁瓣杂波区的平均损失约1 dB,脉宽跳变情况下旁瓣杂波区的平均损失约1.6 dB,3DT处理时脉宽捷变造成的损失与最优STAP处理时近似;与脉宽滑变相比,脉宽跳变情况下的输出SCNR损失凹口较窄,但旁瓣杂波区的损失较大,凹口较窄是由于脉宽跳变下多普勒主瓣展宽较小(由第2.2节的分析可知),损失较大是由于脉宽跳变下脉宽随机变化,空时导向矢量失配较严重;相同条件下时宽-带宽积越大,凹口越窄,输出SCNR损失越小。定义平均能量损失为旁瓣杂波区输出SCNR损失的均值。图9给出了BT=1 000条件下脉宽滑变时旁瓣杂波区(多普勒范围为(±0.15,±0.5))的平均能量损失与归一化脉宽变化量和输入CNR的变化关系图,由图中可知,输入CNR低于40 dB和脉宽变化0.5条件下平均能量损失小于1 dB。

图8 输出SCNR损失对比Fig.8 Output SCNR loss comparison

图9 旁瓣杂波区平均能量损失Fig.9 Average energy loss in side-lobe clutter area

3 结束语

本文针对脉宽-调频极性脉间联合捷变的LFM捷变波形,分别从模糊函数、目标相参积累峰值增益损失、单通道MTI性能和空-时处理性能4个角度对其特性和相参处理能力进行了分析。最后,本文通过仿真实验说明了该捷变波形具有较高的互相关隔离度和良好的相参处理能力。本文的理论分析对工程应用具有一定的指导意义,为杂波背景下脉间捷变相参提供了一种途径。