基于顺序统计滤波和二元积累的辐射源信号检测方法
2022-04-07赵忠凯
赵忠凯, 弓 浩, 张 然
(1. 哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001; 2. 哈尔滨工程大学先进船舶通信与信息技术工信部重点实验室, 黑龙江 哈尔滨 150001; 3. 北京航天长征飞行器研究所, 北京 100076)
0 引 言
近年来,反隐身、低截获概率(low probability of interception,LPI)和超宽带技术已成为雷达设计的发展趋势。与此同时,如何对雷达信号进行侦察也成为当前的研究热点。现代雷达采用宽带线性调频、相位编码等LPI波形,发射功率较低,因此到达侦察接收机的辐射源信号信噪比较低,直接对其侦察有很大的难度,可以归结为低信噪比条件下的辐射源信号检测问题。
为解决低信噪比信号检测困难的问题,相关学者提出了许多信号检测算法。其中,文献[12]针对被动雷达的弱目标提出了基于概率直方图目标检测频度分布来检测目标,能有效检测低信噪比信号,但其准确率受虚警概率影响较大,且需要一定的观测时间才能准确检测目标,实时性较差。文献[13]采用基于经验模态分解的信号检测算法来完成对低信噪比信号的检测,虽然性能相较于常用的能量检测法略有提升,但算法复杂度和计算量增加。文献[14]在复高斯白噪声背景下,从似然比检测形式入手,推导了检测阈值的近似闭式解,虽然实时性得到了一定提升,但计算过程中仍需要高维积分运算,其门限估计需要一定的运算量,复杂度相对较高。文献[15]提出了一种基于累积算法提高弱目标信噪比的方法,采用非相干和相干的方法来提升检测性能,但是这种方法提升效果与积累时间相关,实时性相对较差,且无法用于侦察接收机来提取同步脉冲。综合以上及现有文献检索结果表明,在低信噪比条件下的信号检测方法有一定的局限性,比如算法复杂度高、运算量大和实时性较差等。
对于宽带数字接收机来讲,具备实时性高的低信噪比信号检测方法能使接收机更好地适应当前复杂电磁环境。数字信道化技术具有较大的监测带宽、出色的降噪能力以及多信号分离能力,常常作为雷达侦察接收机中信号预处理的第一步,是准确高效完成侦察任务的关键。通过信道化处理,不仅可以实现对不同频段信号的处理以及降低数据流速率,还可以有效地滤除带外的其他噪声,提高信噪比,以降低后续检测难度。顺序统计滤波是一种有效的恒虚警(constant false alarm rate,CFAR)技术,因其检测门限在均匀和非均匀雷达回波条件下能有效应对复杂信号干扰环境,得到了广泛的应用。在雷达信号检测过程中,为进一步降低门限检测时的虚警和漏警现象,提高检测结果的可信度,提出了二元积累技术。
本文在高斯白噪声背景下,以脉冲信号为处理对象,分别针对数字信道化处理增益以及顺序统计滤波和二元积累的实现方法进行相关的分析和理论推导,并结合实验进行了仿真验证。
1 辐射源信号检测方法
由上文可知,LPI辐射源信号可以归类为低信噪比信号,本节将对其进行建模分析。
本文算法总体处理框图如图1所示,该算法需要利用顺序统计滤波来实现检测,前提是接收带宽内噪声分布是平稳的,比如白噪声分布。首先,利用数字信道化技术对低信噪比信号进行预处理,从而提升信噪比;其次,在同一时刻对各子信道并行输出的信号幅度进行顺序统计滤波,得到CFAR检测门限,并对各子信道进行门限检测;最后,对门限检测结果采用二元积累技术进一步改善检测性能。
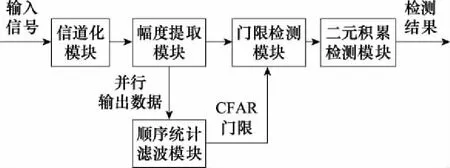
图1 辐射源信号检测方法总体处理框图Fig.1 Overall processing block diagram of the radiation source signal detection method
1.1 数字信道化增益
本文采用了基于多相滤波的高效数字信道化结构,其通过一组多相滤波器来实现对不同频段信号的处理,可以降低数据流速率,能对信号进行有效降噪,降低后续信号检测的难度。
下面将在高斯白噪声背景下,对数字信道化接收机输出的信号复包络进行建模,分析信道化的实际处理增益。
信道化模块的输入信号模型可表示为
()=()+()
(1)
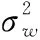
输入信噪比表示为
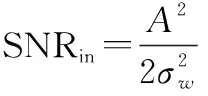
(2)
经过信道化后,第个子信道的输出信号为
()=()+()
(3)
式中:()为滤波器输出的复基带信号;()是经过滤波器输出的复基带噪声,分别表示为
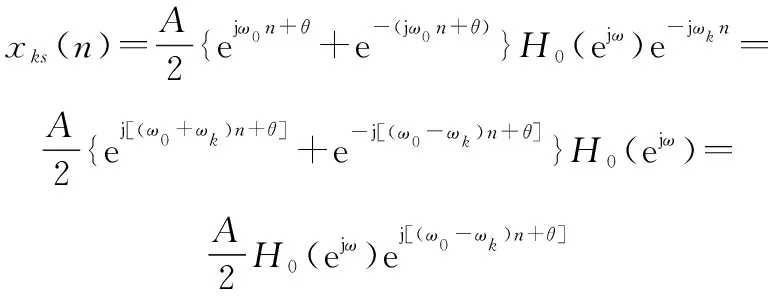
(4)
()=()ej*()
(5)
式中:是第个子信道的中心频率;()是原型低通滤波器的时域响应;(·)是其对应的频域响应;*表示卷积。则输出信号与噪声平均功率表示为
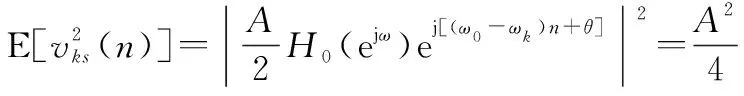
(6)
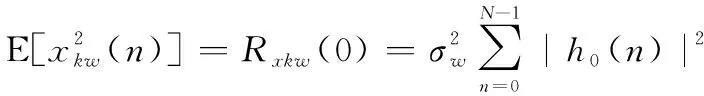
(7)
式中:(·)为复基带噪声()的自相关函数;为滤波器阶数。则输出信噪比可表示为
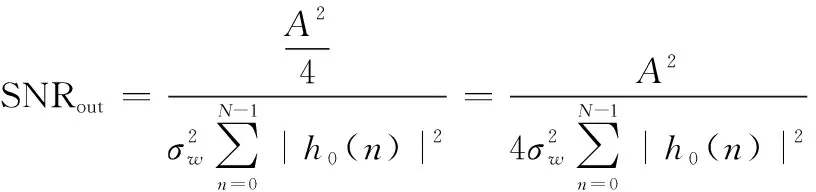
(8)
综上,输出信噪比与输入信噪比比值表示为
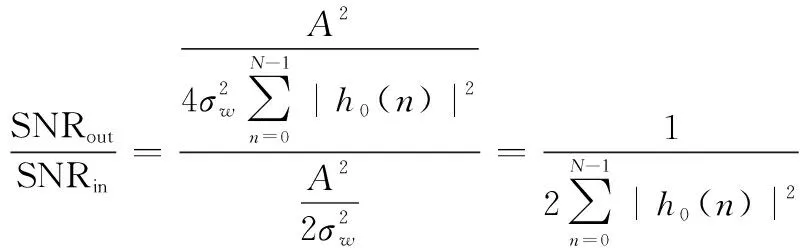
(9)
由式(9)可知,信道化实际处理增益与输入信噪比无关,只与设计的原型滤波器有关。
1.2 顺序统计滤波处理流程
假设信道化处理有个子信道,每个信道采样点数为,其中假设H表示纯噪声输入的情况,假设H表示有信号输入的情况。
对信道化输出信号可以建立数学模型如下:
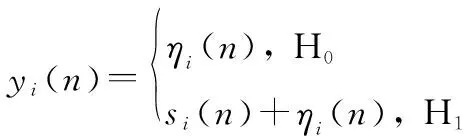
(10)
式中:=1,2,…,;=1,2,…,;()表示第路子信道输出信号;()表示第路信道接收到的信号;()表示加性高斯白噪声。
为了便于工程实现,在相对稳定的信道环境内,对所有子信道选择并行流水型结构的输出模式,在同一时刻对输出数据进行处理,可以提高检测速度。处理流程如图2所示,输出步进可自行选择,一般设为信道数的整倍数。本节以输出步进为1,即参考样本点数为时进行讨论。

图2 顺序统计滤波流程示意图Fig.2 Schematic diagram of ordered statistical filtering process
由图2可知,其处理流程如下:第一步,对子信道数据并行接收,将第次输出的参考样本表示为{(),(),…,(),…,()};第二步,对参考样本进行顺序统计,按照升序排列,得到顺序统计量为{(),(),…,()(),…,()()}并选择出最优顺序统计量记为()();第三步,将其与CFAR门限阈值因子相乘得到检测门限,记为=·()()。
经过一系列处理,恒虚警门限最终可表示为={,,…,}。此外,需要注意的是,最优顺序统计量()()的序号应取不超过08的最大整数,需要按照实际需求进行选择。
1.3 二元积累处理流程
为了改善门限检测后的虚警和漏警现象,对门限检测结果利用二元积累进行处理,进一步降低虚警概率,同时提高检测概率。
二元积累检测又称“”检测,其检测流程如图3所示。首先,对子信道的输出幅度进行滑动窗口长度为点的门限检测,在第次滑窗中第点的比较器结果记为;然后,将第次滑动窗口中的检测结果送入二元积累模块进行二次判决;最后,输出最终检测结果。

图3 二元积累流程图Fig.3 Binary accumulation flow chart
在滑动检测过程中,若窗内次检测中有次成功检测,则认为该窗内有信号存在,记为“1”;反之无信号,记为“0”。在子信道中,第次滑窗的二元积累结果可表示为
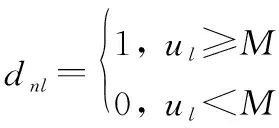
(11)
式中:表示第次滑窗内检测结果的积累值,可表示为

(12)
式中:表示子信道中滑窗内第点的检测结果,可表示为
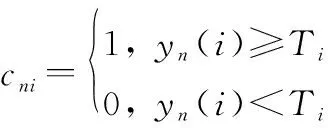
(13)
式中:()表示子信道中第点的信号幅度;表示第点对应的检测门限。
2 门限阈值因子的确定及概率推导
本节主要针对CFAR门限阈值因子以及检测概率的确定问题进行相关理论推导与分析。
2.1 门限阈值因子的确定
为证明经顺序统计滤波处理得到的CFAR检测门限具有CFAR性质,同时给出对应的CFAR概率下的阈值乘积因子,本节将在高斯白噪声背景下,进行如下推导:
(1) 确定输出幅度的概率密度函数(probability density function,PDF)及其分布函数。
在假设下,即纯噪声输入时,子信道输出复信号的瞬时包络值()服从瑞利分布。为表述方便,后续推导过程中记为,顺序统计量统一用()表示。
各包络值的PDF可表示为
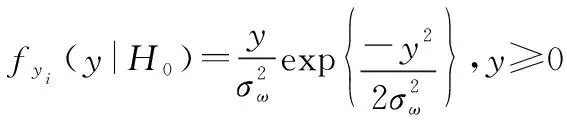
(14)
进一步可推累积分布函数(cumulative distribution function,CDF)为
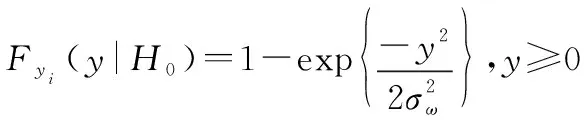
(15)
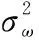
(2) 推导最优顺序统计量()和门限的PDF。由上文可知,检测门限为=·()中的最优顺序统计量()的PDF可表示为
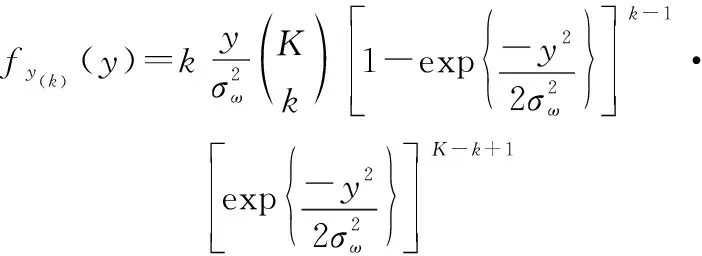
(16)

综上,检测门限的PDF可表示为
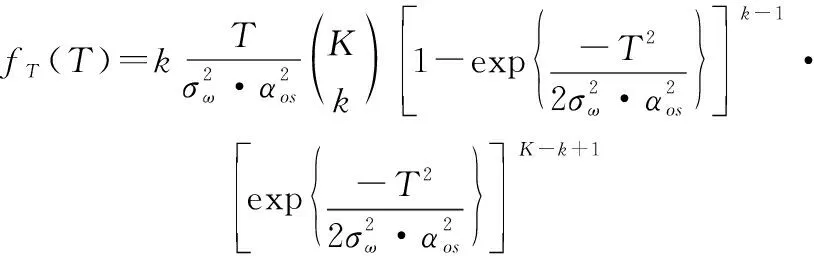
(17)
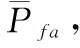
对于给定的检测门限,在该处的虚警概率可表示为
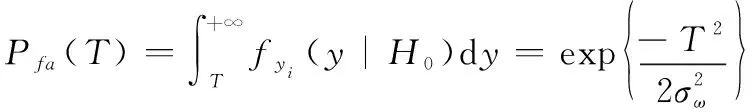
(18)
则平均虚警概率表示为
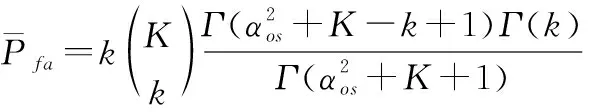
(19)
式中:(·)表示的是伽马函数,其表达式为

(20)
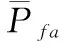
2.2 相关概率的理论推导
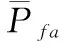

(21)
在假设H下,即有信号输入时,信道输出瞬时包络服从广义瑞利分布,即莱斯分布,可表示为
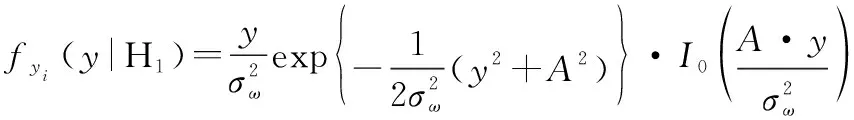
(22)
式中:为输出瞬时信号包络;(·)为修正的0阶第一类贝塞尔函数,记为
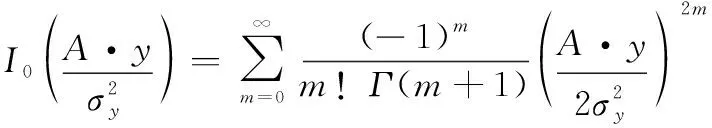
(23)
某采样点处对应门限,其检测概率表示为
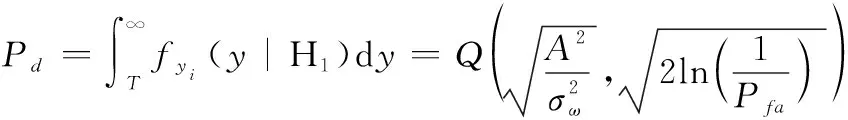
(24)

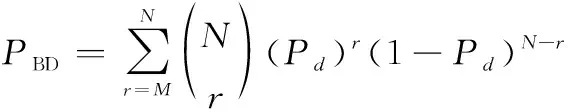
(25)
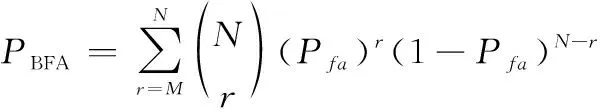
(26)
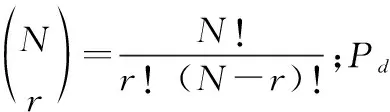
3 仿真实验
在以下仿真实验中,输入采用实信号,监测频率范围为1 250~1 750 MHz,系统采样率=1 200 MHz,信道数为32。由于信道化结构特性,1~16信道和17~32信道的输出共轭对称,故只需对前16信道输出信号进行检测即可。系统虚警概率设置为10~10,对在监测带宽内的频率随机的单频脉冲信号进行检测。
3.1 信道化增益仿真分析
数字信道化的原型滤波器[]的设计参数为:通带截止频率=1875 MHz,阻带截止频率=375 MHz,通带波纹为=001 dB,阻带衰减为=60 dB,可得到一个192阶的原型低通滤波器。
由式(9)计算可知本文设计的滤波器组的理论增益值为1086 dB。输入单频脉冲信号,在各信噪比下分别进行1 000次仿真实验,得到信道化输出信号在不同输入信噪比条件下的信噪比增益结果如表1所示。

表1 信道化处理增益Table 1 Channelization processing gain
可以看出,实际仿真结果与理论值的误差在0.03 dB以内。由此说明,在考虑滤波器过渡带的影响下,信道化处理增益只与设计的原型滤波器有关,结论正确。
3.2 顺序统计滤波性能仿真分析
下面将对顺序统计滤波相关的性能进行仿真分析。
由式(19)可知,在CFAR条件下,参考样本点数和最优顺序统计量的序号的选取会影响门限阈值因子的值,从而影响检测效果。
在不同和取值时,虚警概率与门限因子的关系如图4所示。
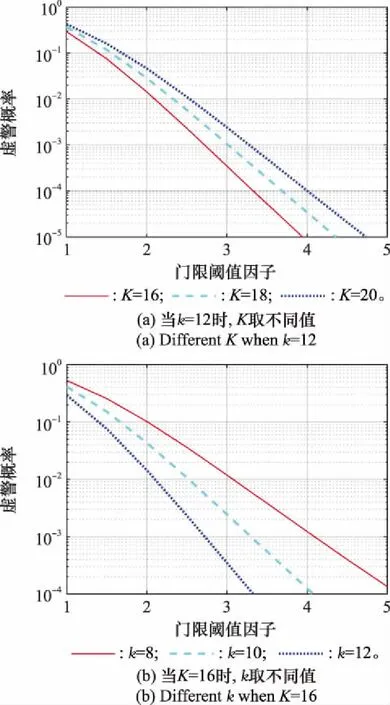
图4 虚警概率与门限阈值因子的关系Fig.4 Relationship between the false alarm probability and the threshold factor
由图4(a)可以看出,在同一虚警概率下,固定顺序统计量序号=12时,值越大,门限阈值因子值越大;由图4(b)可以看出,在同一虚警概率下,固定参考样本点数=16时,值越大,门限阈值因子值越小。需要注意的是,如果值过大将会影响其抗干扰数目容限,因此需要根据实际情况适当选取值,通常取不超过08的最大整数。
3.3 二元积累性能仿真分析
下面对二元积累相关的性能进行仿真分析。由式(25)和式(26)可知,二元积累可以对单次检测概率和虚警概率进行积累,以改善检测性能。“”准则的策略最优需要满足以下条件:一是累积检测概率大于,二是累积虚警概率小于等于。
如图5所示,对二元积累和的取值问题进行了分析,其纵坐标为积累概率与单次概率之比,如果值大于1,说明概率得到了提高;反之则降低。
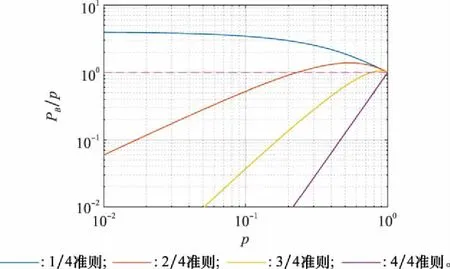
图5 “M/4”准则下积累概率与单次实验概率的比值Fig.5 Ratio of the cumulative probability to the probability of a single test under the “M/4” criterion
由图5可看出,在固定=4的条件下,单次实验概率不断增大时,取值不同会影响积累效果。比如,“14”准则下,对虚警和检测概率都进行了提升;“44”准则下,对虚警和检测概率都进行了降低,显然这两种情况不符合实际需求;对于“24”准则和“34”准则,两者虽然都能对较小的值进行降低,但“24”准则对于小至023的值也能改善检测概率。故综上所述,“4”准则中,“24”准则是最优策略。
由式(26)可知,如果要求系统虚警概率达到10以上,那么在利用顺序统计滤波估计检测门限时,其门限阈值因子的估计所需的虚警概率如表2所示。可以看出,在“24”准则下,二元积累可以有效降低虚警概率。

表2 二元积累前后的虚警概率对比Table 2 Comparison of false alarm probability before and after binary accumulation
为了更加直观地观察“24”准则下,二元积累对于虚警和误警现象的改善效果,在虚警概率为=10的条件下,进行了仿真。
输入频率为1 502 MHz的单频脉冲信号,其脉宽为667 μs,信噪比为-2 dB,各部分仿真波形如图6所示。
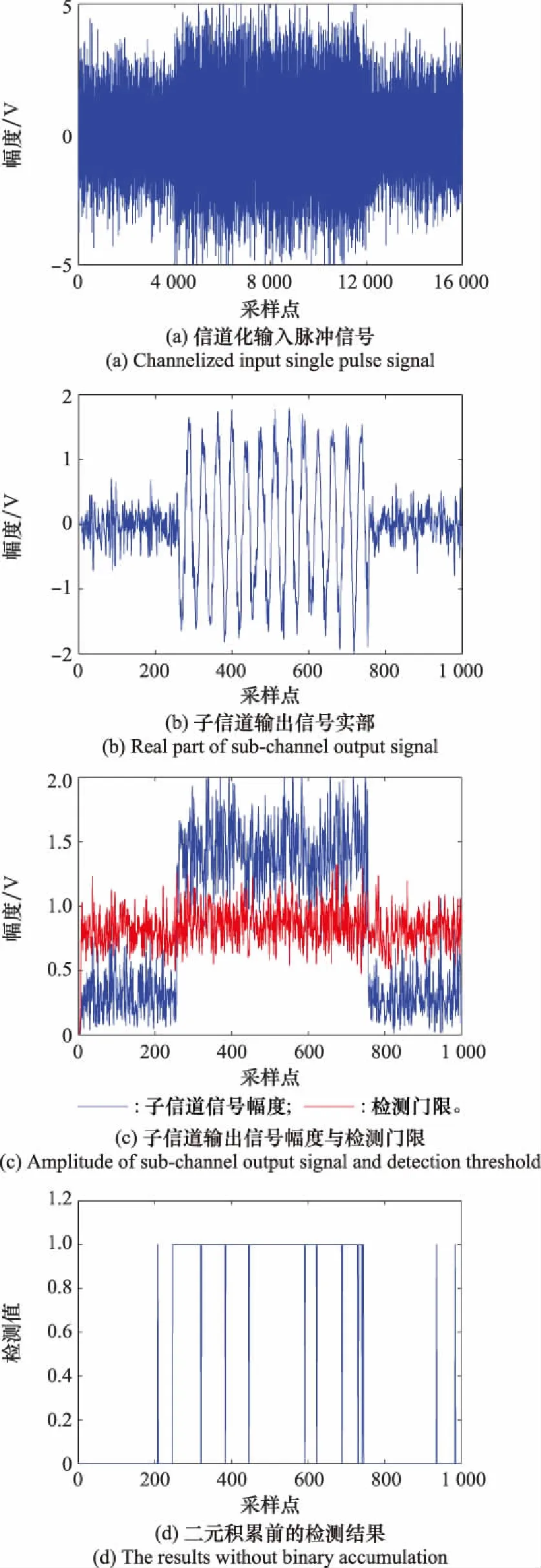
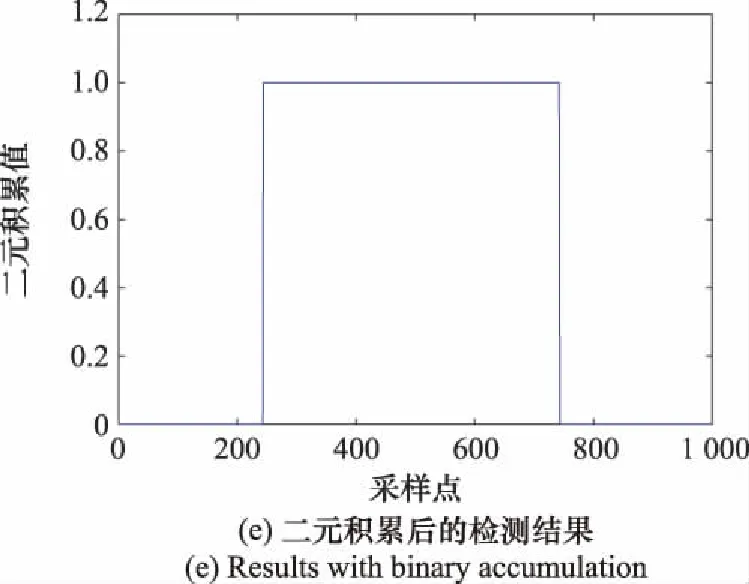
图6 信号检测过程示意图Fig.6 Schematic diagram of signal detection process
图6(a)是输入的低信噪比信号,可以看出很难直接对其进行检测。图6(b)是第9信道输出复信号实部的波形图,可以观察到很明显的降噪效果。图6(c)是子信道输出信号的幅度与检测门限示意图。图6(d)是门限检测结果,可以看出,在信噪比为-2 dB的条件下进行检测时会出现一定的虚警和误警现象。图6(e)是对门限检测结果进行二元积累后的处理结果,可以看出,虚警和误警现象都得到了修正,说明二元积累可以在提高检测概率的同时降低虚警概率。
3.4 检测概率仿真分析
下面对本文算法的检测概率仿真并进行统计分析。
由式(24)和式(25)可确定本文方法的理论检测概率,如图7(a)所示。
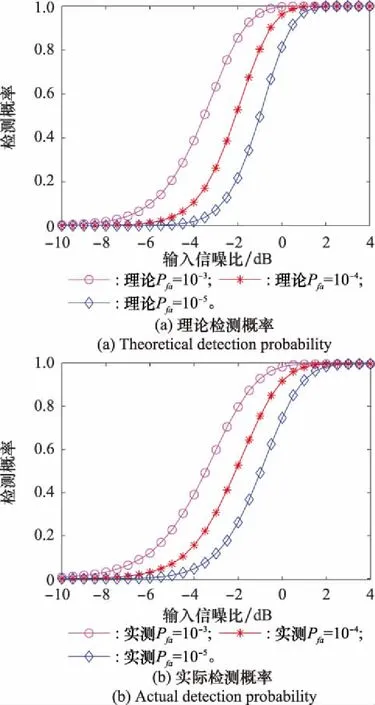
图7 理论与实际检测概率曲线对比Fig.7 Comparison of theoretical and actual detection probability curves
为验证检测概率与理论是否相符,在系统虚警概率为10~10的条件下,对在监测带宽内的频率随机的单频脉冲信号进行检测。顺序统计滤波模块中,参考样本点数取=16,最优顺序统计量样本值序号取=12,选择“24”准则进行二元积累检测。
在不同信噪比条件下进行仿真试验,经统计得到实测检测概率如图7(b)所示。
由图7可以看出,实测检测概率曲线与理论检测曲线基本吻合。在上述仿真条件下,要求系统虚警概率10时,在信噪比09 dB处,可以达到90%以上的检测概率,实现了低信噪比条件下辐射源信号的准确检测。
4 结 论
本文针对辐射源信号检测困难的问题,提出了一种新的信号检测方法,利用数字信道化对大监测带宽内的信号进行信噪比提升,然后采用顺序统计滤波和二元积累技术进行了CFAR检测。实验结果表明,在虚警概率为10时,对信噪比高于09 dB的辐射源信号可以达到90%以上的检测概率,实现了低信噪比下信号的准确检测。
本文算法复杂度小,解决了目前低信噪比信号检测算法复杂度高、运算量大的技术难题。该方法实现结构相对简单,采用了适合在工程实现的并行流水线结构,提高了检测速度和实时性。仿真实验证明了所提方法的有效性和正确性,为辐射源信号被动检测提供了有力的理论支撑。
