基于神经网络的高超声速飞行器惯导系统精度提高方法

胥涯杰, 鲜 勇,*, 李邦杰, 任乐亮, 李少朋, 郭玮林

(1. 火箭军工程大学作战保障学院, 陕西 西安 710025; 2. 中国人民解放军63768部队, 陕西 西安 710043)

0 引 言

高超声速飞行器具有打击距离远、飞行时间长等特点,而且依靠其独特的气动外形,具有滑翔机动能力,使对方防御拦截系统难以预测其轨迹,因此是现代战场的“杀手锏”武器[1-2]。

高超声速飞行器飞行全程的可靠性与精确性都离不开惯性导航系统作支撑。捷联惯性导航系统(strapdown inertial navigation system,SINS)具有结构简单、成本低、体积小等优势[3-4],加上计算机技术高速发展带来计算速度的提升,其越来越多地运用到武器系统中。加速度计和陀螺仪是SINS的测量元件,其误差大小直接决定了整个惯导系统的精度高低[5-7]。常见减小惯性器件测量误差的方法有:一是从元器件自身属性入手,通过提高制造工艺,生产更加稳定、精确的惯性器件;二是通过引入惯性系统误差补偿模型,对静态误差进行补偿与修正。

目前我国高精度惯组测量元件主要采用的是石英挠性加速度计和激光陀螺仪,而要想更进一步地提高惯导测量元件的制造精度,需要多个领域投入长时间攻关研究,所以短时间内从工业制造水平上提升惯导精度还难以有较大突破。因此,目前大多数学者主要是对第二方面进行研究,通常在惯性系统使用前在高精度转台进行多位置和速率标定方法得到静态误差系数,并对系统静态误差予以补偿[8-15]。其中，文献[8]基于建立误差参数与导航误差间的线性关系,为充分激励惯性器件各项误差参数,设计多位置连续旋转方案,利用卡尔曼滤波方法对标定的数据进行处理,进而得到较为准确的陀螺仪和加速度计各项静态误差系数。文献[9]利用温箱双轴转台可以更快速、高效地标定出21个误差参数。文献[10]通过设计的26个位置及其优化的12位置选装方案,更便于标定过程中分离出干扰因素。文献[11]所提方法可以降低标定对转台精度的依赖,提升了低成本条件下的标定精度。文献[12-14]考虑对3个轴上加速度计的加速度敏感点不重合产生的尺寸效应进行补偿,克服了传统分立式标定方法的不足,得出了尺寸参数。文献[15]通过在精密离心机上进行多位置和多转速测试,对加速度计非线性误差项进行激励,可以标定出部分非线性误差系数,进一步完善了误差补偿模型,使其更接近惯性导航系统真实的物理模型。虽然上述各种误差补偿的方法可以有效弥补惯性系统因静态误差引起的系统误差,但是在标定完成后因运输、存储等影响会使标定值与真实值之间产生偏差,这样的动态误差将导致误差补偿方法的精度下降。而且由于与视速度二次项及更高阶相关的系数不便得到(即使是高精度离心机,也仅能标定出少量非线性误差系数),使用的误差模型通常只含零次项与一次项误差系数,与惯性系统的实际模型还存在偏差。

此外,还有很多学者利用卫星、地磁、天文等外界信息,辅助惯性系统提高导航精度[16-22]。其中，文献[16-18]利用卡尔曼滤波及其拓展方法,对全球定位系统(global positioning system, GPS)信号与惯性导航信号进行数据融合。文献[19-20]利用地磁信息,分别对惯性系统误差模型和导航信息进行校准。文献[21-22]通过星敏感器获取天文信息,抑制了惯性系统的累计误差。但是,此类外界信息的抗干扰能力差,加之高超声速飞行器在飞行过程中可能出现“黑障”[23]等现象,使得这类辅助方法的应用场景有限。为适应复杂多变的战场环境,必须要对纯惯性模式下的导航方法进行研究。

针对在纯惯性导航精度的提高研究上,文献[24]通过神经网络与拓展卡尔曼滤波方法相结合,在GPS失效后利用训练得到网络对滤波参数进行纠正。文献[25]通过智能优化算法对惯性系统的误差参数进行在线辨识,在天地一致性上更佳。但是,上述方法均无法避免模型误差带来的影响。

本文摒弃传统根据惯性系统物理特性构建误差补偿模型方法,通过构建拟合惯性器件输入与输出关系的神经网络模型,采取对飞行过程中的导航数据和惯组输出脉冲收集,而后在线训练得到实际飞行过程中的惯性导航系统模型,然后在线使用训练该模型进行导航。仿真表明,该方法能得到比误差补偿模型更准确的惯性系统模型,有效提高了高超声速飞行器惯性导航精度。

1 SINS导航模型及其误差分析

SINS导航计算模型如下所示：

(1)

式中:Ra表示发惯系下的位置；Va表示发惯系下的速度；Wa表示发惯系下的视速度；ga表示发惯系下的重力加速度。因为SINS的惯性器件采集得到的是弹体系下的视速度增量Wb,需要将其转换到发惯系下,坐标转换如下所示:

(2)

捷联惯导计算模型总结如图1所示。

由图1可知,对惯性测量器件输出数据的处理好坏,直接决定着整个SINS系统所提供导航值的准确性。但是惯性测量器件的输出不仅是对所敏感物理参数的反映,还包括惯性器件本身制造工艺偏差带来的误差(静态误差),以及环境干扰引起的误差(动态误差)。目前高精度的陀螺仪主要是光纤陀螺和激光陀螺,具有环境适应性强,长期稳定性好的优点[28-29],因此本文主要考虑加速度计测量器件误差对惯性系统的影响。

为减小静态误差,通常在惯性系统使用前通过对其进行标定,得到静态误差系数,采取带静态误差系数的模型对惯导进行补偿。惯性测量组合实际测量值一般采取脉冲采样的方式进行,惯性器件不断向弹载计算机发送脉冲信号[30],加速度计测量误差模型如下所示:

(3)

由加速度计脉冲增量ΔNb得到弹体系下视速度增量ΔWb需要对式(3)进行反解,略去小量做一定简化后的捷联惯导加速度计误差补偿模型如下所示:

(4)

虽然用该误差补偿模型的方法能有效降低惯性器件自身带来的静态误差,但是精度还是受限于数学模型与实际惯性系统物理模型的逼近程度。而且在实际运用中,与视加速度平方或其乘积成比例的二次项及其他高阶项前的误差系数很难得到准确值,因此无论采取什么样的补偿措施,都会因使用的误差补偿模型存在一定的模型偏差而降低补偿精度。

此外,高超声速飞行器惯性系统从标定环节到实际飞行环节,会受到储存、搬运过程等带来外部环境的干扰以及对惯性系统每次通断电引起的逐次通电误差,这些因素的存在会使惯性器件从标定状态发生改变。如果误差补偿模型仍然使用之前标定的静态误差系数,产生导航偏差将不可避免,但是目前误差补偿模型还难以较好地处理对此类动态误差。

在高超声速飞行器的飞行过程中,因惯性系统误差引起的导航偏差将会随着长时间累积变得很大,对有全程高精度制导要求的飞行器是十分不利的。鉴于传统误差补偿模型处理两类误差能力的局限与不足,本文提出一种神经网络导航方法:在高超声速飞行器的飞行前期,认为能够接收到可靠准确的卫星导航值,收集这一阶段每个采样周期下的速度位置信息和惯性系统中测量器件产生的脉冲值,对构建的神经网络进行在线训练,训练完毕后,将其代替传统误差补偿模型。这种在线训练、在线使用的方法,只需关注惯性导航系统输入与输出之间的关系,不再对其具体的物理模型进行研究,这样可以有效降低原误差补偿模型因模型偏差带来静态误差的影响。而且,在线训练的方式是直接对飞行器惯性系统在飞行状态下进行研究,这样还能避免受到逐次通电等外界条件带来动态误差的影响。

2 神经网络模型

鉴于加速度计的测量值是根据自身产生的脉冲输出值确定,可认为加速度计脉冲增量ΔNb与弹体系下视速度增量ΔWb之间存在多输入与多输出映射关系：

(ΔWxb,ΔWyb,ΔWzb)=f(ΔNxb,ΔNyb,ΔNzb)

(5)

如果考虑能用一个合适的神经网络拟合其映射关系f,那么就能实现不考虑惯性系统物理模型的条件下,代替原误差补偿模型。

反向传播神经网络(back propagation neural network, BPNN)具有强大的非线性映射能力且结构简单的优点[31],因此选择构建以(ΔNxb,ΔNyb,ΔNzb)为输入、(ΔWxb,ΔWyb,ΔWzb)为输出的三输入三输出的BPNN结构。根据模型复杂度需求,选择含有一个隐藏层的网络进行训练,激活函数采用指数函数tansig,输出层激活函数选用线性函数purelin,表达式为

(6)

(7)

训练算法采用Levenberg-Marquardt(L-M)算法[32],该算法是牛顿法的改进,能够避免在雅克比矩阵奇异或病态时发生不收敛的情况。该算法通过直接计算黑塞矩阵,从而减少了训练中的计算量,对于中等规模的BPNN有最快的收敛速度。

隐藏层的节点数采取网络结构增长型方法确定,其经验公式为

(8)

式中:a,b分别为输入和输出的节点个数；α为1～10的常数,因此本文选取s的取值范围为4～14。统计在相同训练时间下,具有不同隐藏层节点数的BPNN分别在3个方向上的训练误差如表1所示。

表1 不同隐藏层节点的训练效果Table 1 Training effect of different hidden layer nodes

由表1可知，在隐藏层节点数为6的结构下,3个方向的训练误差都是最小的,所以把隐藏层节点设为6,由此便将BPNN结构模型确定下来,如图3所示。

3 仿真设计与结果分析

3.1 仿真设计

根据高超声速飞行器的运动特性,按照文献[33]建立的动力学模型,设计一条由三级发动机助推的运动轨迹。不考虑卫星导航误差,记录每个采样周期下加速度计产生的脉冲数和发惯系下的速度位置信息。

产生标准样本的条件是:不考虑静态误差系数因外界干扰带来的漂移;用带二次项静态误差系数的误差补偿模型作为惯性系统的模型,即用式(3)的加速度计脉冲产生模型和式(4)的加速度计误差补偿模型。

为对比训练得到神经网络模型的精确性,分别设计惯性系统在两类误差条件下的导航实验。

动态误差方面,主要测试逐次通电误差对惯性导航精度的影响。由于安装误差相对比较稳定，以及二次项静态误差系数的准确值本身很难获取,因此不考虑逐次通电误差对其影响。对加速度计的零次项和一次项误差系数K0x、K0y、K0z、K1x、K1y、K1z加入逐次通电误差产生的漂移,即脉冲产生模型不再是式(3)而是如下所示:

(9)

静态误差方面,主要考虑所构建误差补偿模型与惯性系统实际物理模型间的偏差对导航影响。虽然构建式(3)包含二次项误差系数的补偿模型在仿真条件下可以实现,但由于难以得到其准确值,实际应用中的惯性系统误差补偿模型误差系数通常只包含零次项和一次项。因此,选择用误差补偿模型是否考虑二次项来观测模型偏差对惯性导航精度的影响,即可认为在有模型偏差的条件下不考虑二次项误差系数情况,此时加速度计的补偿模型为下式所示：

(10)

3.2 数据生成及网络训练

最接近真实惯性系统物理模型的是第3.1节中给定的标准条件(无模型误差、无逐次通电误差),使用该条件下产生的数据为标准导航值,作为其他条件下的对比对象。

在考虑有逐次通电误差对惯性系统产生动态误差时,通过对误差系数加入随机偏差(标准正态分布)的方式产生,其精度设计如表2所示。按照蒙特卡罗模拟方法随机生成100组数据,作为逐次通电误差对导航精度影响的测试样本。

表2 逐次通电误差漂移值(1σ)Table 2 Drift value of power-on error (1σ)

在考虑对比无二次项误差系数对惯性系统带来静态误差时,不考虑误差补偿模型中各误差系数的漂移。

为了让训练得到的网络能够胜任惯性系统后续的测量任务,必须保证选择作为训练样本的数据在各个方向上都有足够的覆盖性。又由于高超声速飞行器在主动段和无动力滑翔段的飞行特点有显著差异,而无动力滑翔段主要在较小的范围内变化,因此选用主动段以及主动段结束后的一段飞行时间数据作为训练样本。训练完成以后,用神经网络模型替代加速度计原补偿模型,得到发惯系下神经网络导航方法的导航数据。

为确保神经网络得到有效收敛,而且又不消耗过多的时间来训练,因此需要设置合适的训练步数。按照第2节确定的神经网络结构,其损失函数下降曲线如图4所示。由图4可以判读约在第5 000步损失函数收敛到10-10量级,之后损失函数几乎不再下降,由此确定网络的训练步数为5 000。

在Xeon(R) CPU E3-1230(3.3 GHz)单核单线程计算模式下,单次训练步数为5 000时,对所建网络训练100次的耗时情况进行统计:最长用时为23.4 s,最短用时为20.3 s,平均用时为21.2 s。可见,在对训练数据收集完毕后,只需要很短的时间就可以完成该模型的训练。

3.3 结果分析

3.3.1 与动态误差对比

首先测试神经网络导航方法与存在动态误差下误差补偿模型方法在导航精度上的差异。为验证方法的可行性,先检验给定逐次通电误差给误差系数造成漂移量在一倍标准差的情况下,对比误差补偿模型方法和神经网络方法在惯性系统独立工作1 300 s后的导航结果。同时,加入参数在线辨识方法[25],使用文中对参数的辨识精度,将该精度下的导航结果作为对比。

图5(a)～图5(c)是3种方法的速度导航偏差对比,图5(d)～图5(f)是位置导航偏差对比。

根据图5可以看出,存在动态误差情况下的误差补偿方法随着飞行时间的累计,造成X和Z方向的速度导航偏差逐渐增大。而由于飞行器在Y方向有先上升再下降的运动特性,使之前在上升段累积的偏差在下降段有所减小,但随着下降段时间的延续偏差值又开始增大,因此造成了图5(e)显示的速度导航偏差先增大后减小。综合来看,3个方向上的无论是在速度还是位置方面,在导航的精度上,神经网络导航方法都比存在动态误差情况下的误差补偿方法及参数在线辨识方法高,说明该方法是有效的。

为充分验证方法的普适性,下面对100个随机生成的逐次通电误差漂移值下的惯性系统进行测试并做出统计,图6是对测试样本在惯性系统独立工作1 300 s后,分别采用参数在线辨识和神经网络导航方法的位置导航偏差统计图。

由对比结果可以发现,在线训练、在线使用的神经网络导航方法不仅是可以明显降低因惯性系统动态误差引起的导航偏差量,而且比参数辨识方法的精度更高。

表3和表4是100组测试样本在使用参数在线辨识方法下的位置导航偏差统计结果,表5和表6是测试样本使用神经网络方法位置导航偏差大小的统计结果。

表3 在线辨识方法位置导航偏差分布表Table 3 Position navigation deviation distribution of on-lineidentification method

表4 在线辨识方法位置导航偏差统计表Table 4 Position navigation deviation statistics of on-lineidentification method m

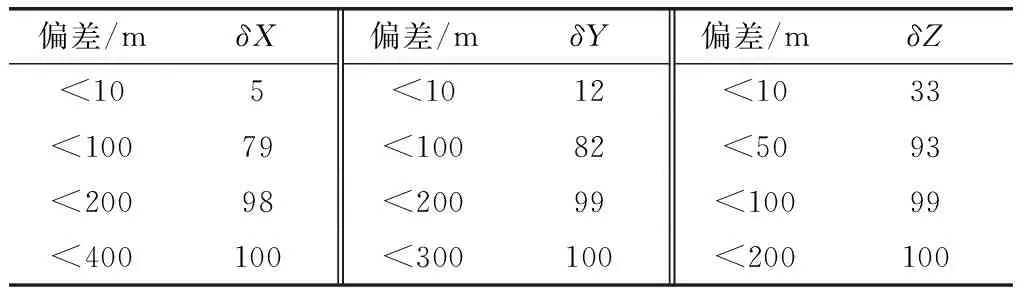
表5 基于BPNN的位置导航偏差分布表Table 5 Position navigation deviation distribution based on BPNN

表6 基于BPNN的位置导航偏差统计表Table 6 Position navigation deviation statistics based on BPNN m

根据表3和表4可知,采用参数在线辨识方法,大部分样本在测试时间内产生的惯性系统3个方向位置的导航偏差值都达到数百米,还有部分样本偏差值超过1 km。表5和表6的统计结果显示，用在线训练的神经网络方法是能够对不同逐次通电误差下的惯性系统有很好的在线辨识效果,测试样本中大部分位置导航偏差都只有几十米,导航精度明显优于前者。

3.3.2 与静态误差对比

测试得到神经网络导航方法与不加二次项误差系数的误差补偿模型方法在速度导航偏差结果对比(见图7(a)～图7(c)),及在位置上的导航偏差结果对比(见图7(d)～图7(f))。

从仿真结果来看,模型误差类的静态误差对导航偏差的影响远低于逐次通电误差类的动态误差。由图7(a)和图7(d)看出，在x方向上,神经网络方法在测试时间前期,其速度位置导航偏差略大于误差补偿模型方法,但随着时间增加,误差补偿模型的偏差逐渐超过神经网络导航方法的偏差。总体而言,尽管模型误差造成的导航偏差较小,而神经网络方法的导航偏差更小,说明神经网络能训练出更逼近真实惯性系统的模型进行导航。

3.3.3 小结

为更直观地观测神经网络方法的导航精度,分别统计存在模型偏差的误差补偿模型(静态误差)、存在动态误差的误差补偿模型(选择漂移值在1倍标准差下的样本)、在线训练得到的神经网络模型,在发惯系下的速度导航偏差(见表7)和位置导航偏差(见表8)。

表7 发惯系下的速度偏差Table 7 Speed deviation in inertial system m/s

表8 发惯系下的位置偏差Table 8 Position deviation in inertial system m

根据表7和表8的对比结果,不难看出在线训练、在线使用的BPNN导航方法相比于因逐次通电误差引起的动态误差导航模型,导航精度能提高2个数量级。相比于因不考虑二次项系数带来误差补偿模型不准确引起的静态误差导航模型,导航精度能提高1个数量级。

4 结 论

本文对高超声速飞行器捷联惯性系统中加速度计模型进行了研究,针对传统补偿模型存在模型误差以及静态误差系数的标定值与实际误差系数值存在偏差两个因素进行分析,说明了传统误差补偿模型方法处理两类误差能力不足的缺陷。利用高超声速飞行器飞行前期在有卫星提供准确导航信息的支撑下,结合BPNN强大的非线性拟合能力,提出了一种在线训练、在线使用的神经网络导航方法,即在飞行器飞行过程的前期收集数据、中期在线训练、后期在线使用。通过仿真对比,该方法的导航精度相比于存在模型误差和逐次通电误差的误差补偿方法能有效提高1～2个数量级。

与传统误差补偿模型方法相比,本文不再对惯性系统测量器件具体物理模型进行研究,而是关注惯性系统的输入和输出数据之间的映射关系,通过搭建合理的神经网络模型,训练得到更加贴近实际惯性系统的模型。此外,直接对飞行过程中的惯性导航系统进行在线训练的方式,同样能避免动态误差对惯性系统的影响。虽然在线收集数据、在线训练的方法对计算机的数据存储能力和运算能力都有很大的挑战,但是随着计算机技术的不段发展,压力也将随之降低,因此该方法具有可行性。然而由于仿真条件与实际环境的差异,该方法还需要在地面测试或飞行试验中进一步研究。