基于载波相位的接收机群时延测量技术

王峰毅, 肖志斌, 李蓬蓬, 张 可, 倪少杰

(国防科技大学电子科学学院, 湖南 长沙 410073)

0 引 言

群时延描述了信号传输所产生的延迟大小,表征了系统和网络的线性失真。在卫星通信领域,群时延表征了系统的传输特性,覆盖包括设计、生产、在轨运行等各个阶段[1]。高精度导航接收机的群时延特性对测距的随机误差和系统误差影响较大[2-5],因此其精密测量尤为关键。

传统的高精度导航接收机群时延测量为单载波相位法,基于群时延的定义,利用矢量网络分析仪进行群时延测量,采用不同频率的单载波信号通过被测通道,利用矢量网络分析仪分析原始单载波信号和通过被测信道后得到的单载波信号的相位和幅度,将其幅度比作为通道的幅频响应,相位差作为通道的相频响应,群时延特性则为相频响应对频率的导数[6-8],其精度与测量分辨率有关,以Agilent公司的HP8720矢量网络分析仪为例,当测量频率分辨率为0.5 MHz时,测试群时延误差为1.2 ns[9-10]。同样,基于群时延的定义,杨丽[11]提出了利用傅里叶变换测量群时延的方法,其测量精度可达0.1 ns。肖志斌[12]提出了基于窄带扩频信号的高精度导航接收机群时延测量方法,该时延估计方法主要基于信号自相关函数，采用早迟码时延估计方法实现对群时延的测量,系统误差估计校准后其测量精度可达0.16 ns。

对于俄罗斯全球卫星导航系统(Global Navigation Sate-llite System, GLONASS)频分多址系统,其接收机群时延主要表现为频间偏差(inter-frequency bias, IFB)[13-14],不同卫星的IFB会导致载波整周模糊度无法固定,从而影响其载波相位的高精度应用及其测距定位性能[15]。GLONASS频分多址系统的接收机IFB主要建模成线性模型[16-18],当IFB与频率呈线性关系时,其整周模糊度固定效果较好,满足实际应用需求。在实际应用中,高精度导航接收机的群时延特性不一定满足上述严格线性约束条件,此时利用传统GLONASS的IFB估计得到的误差较大。载波相位的高精度应用通常需要对接收机通道群时延进行皮秒级测量才能支撑载波整周模糊度固定,常规的基于矢量网络分析仪和码时延的方法在精度上也无法满足要求。

窄带扩频信号经过导航接收机测量得到码时延的同时,还可以测量得到载波相位,其测量精度可以满足皮秒级群时延测量精度,但是载波相位的利用需要精确固定整周模糊度进行支撑[19]。传统的整周模糊度固定方法包括最小二乘模糊度搜索算法[20-21]、快速模糊度解算法[22]和最小二乘模糊度降相关平差法[23-24]等,主要用于配合电文解算进行伪距测量。其中电文的调制和解算等步骤相对于窄带扩频信号直接求解载波相位的方法较为复杂,并且其应用背景主要用于测距,因而不适用于导航接收机通道群时延测量。利用伪距测量结果取整也可以估计出整周模糊度[25],但是其估计结果存在较大误差,当载波频率为1 600 MHz时,误差一般为2～3周,无法准确固定整周模糊度。

由于导航接收机通道特性可以等效于带通滤波器,其群时延特性一般为抛物线特性或三角函数特性[26],满足分段抛物线特性,因此可以利用此先验信息遍历并固定整周模糊度。

基于上述分析,本文提出了一种基于窄带扩频信号载波相位的高精度导航接收机群时延测量技术,经过仿真验证,该方法的测量精度可达皮秒量级,对群时延具有良好的测量效果。

1 群时延的定义及特征分析

在卫星通信领域,一般用群时延特性来表示系统的时延特性,其定义为相位频率特性对角频率的导数[26-29],如下所示:

(1)

式中:φ(ω)表示相频特性;ω表示角频率;τ(ω)表示群时延特性。通常情况下,高精度导航接收机的模拟接收通道特性为非线性相位特性,其群时延特性呈波动特性[30]。通过矢量网络分析仪测得某型号导航接收机群时延特性如图1所示。

将矢量网络分析仪群时延特性测量结果进行平滑,并假设该平滑结果为导航接收机实际群时延特性,如图2所示。

从图2中可以看出,其群时延特性为非线性相位特性,且在通带范围内呈近似抛物线特性。其局部放大图如图3所示。

可以看出,局部群时延可以通过二次函数曲线表示,满足分段抛物线特性,对于段内L个频点(f1,f2,…,fL)的群时延表达式如下:

(2)

式中:τ0表示常数项系数;a表示一次项系数;b表示二次项系数。若能够估计出每段群时延特性的抛物线参数a,b,τ0,则可以得到最终的群时延特性。

2 基于载波相位的群时延测量技术

2.1 测量原理

基于载波相位的群时延测量技术,其测试设备连接框图如图4所示。

利用窄带扩频信号源产生多组待测频带内的窄带扩频信号,通过高精度导航接收机获得伪码和载波相位观测量,进行群时延测量计算。

采用载波相位观测值进行导航接收机群时延测量的原理如下:

(3)

式中:τcarryi为每一段的载波相位群时延测量值,也由窄带扩频信号经过待测接收机通道测得;Ni表示整周模糊度;ωcarryi表示载波相位观测误差,可以忽略不计;τNi为波长,其定义为

(4)

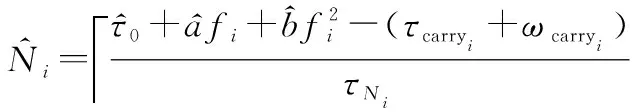
(5)

(6)

只有当给定的抛物线系数正确时,由式(6)求得的群时延特性与真实群时延特性相同,否则会产生差异,定义误差如下:

(7)

可以通过遍历抛物线系数,求取最小误差的方式找到对应正确的抛物线系数,固定整周模糊度,从而计算得到正确的群时延特性。

为保证群时延特性测量结果的连续性,设置后一段的起始点与前一段最后一个点重合。

若将分段二次函数自变量调整为相对频率,即

fi=(i-1)Δfc

(8)

式中:Δfc表示相邻频率差。此时所有段二次函数的自变量都相同,其非常数项系数a,b的遍历范围相似,且抛物线常数项系数即为每一段起始点群时延。因此,对于待测通带范围内的N段群时延特性,第j+1段的常数项系数可以由第j段二次函数直接求出:

(9)

因此除了第一段群时延特性需要遍历所有抛物线系数,其余段只需要遍历抛物线非常数项系数a,b即可。

2.2 整周模糊度固定方法

由于待测群时延具有分段抛物线特性,因此可以将通带带宽分为N段,每段L个群时延测量值。整周模糊度固定方法分为以下3个步骤。

步骤 1遍历并固定第一段群时延特性抛物线系数

对于第一段群时延而言,其抛物线常数项为起始点群时延。若忽略载波相位测量误差,由式(3)和式(8)可以得到:

(10)

式中:ρi(i=1,2,…,L)为每一段的码时延,由窄带扩频信号经过待测接收机通道测得;ωρi(i=1,2,…,L)表示观测误差。

抛物线常数项遍历范围由起始点整周模糊度遍历范围N1决定,可以利用码时延估计起始点整周模糊度的搜索范围,码时延观测量如下所示:

τ0=τcarry1+N1τN1

(11)

由式(10)和式(11)可得

τ0=τcarry1+N1τN1=ρ1+ωρ1

(12)

因此起始点整周模糊度的搜索范围中心为

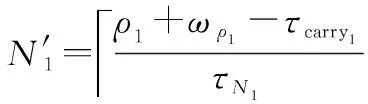
(13)

其搜索范围为搜索中心±N0个整周模糊度。

可以证明,抛物线常数项系数并不影响非常数项系数的搜索固定结果,因此可以先遍历并固定非常数项系数,再遍历并固定起始点整周模糊度。其证明如下。

由式(7)可得,当抛物线常数项系数增加整周模糊度N0,即

(14)

则遍历误差为

(15)

由式(5)可得

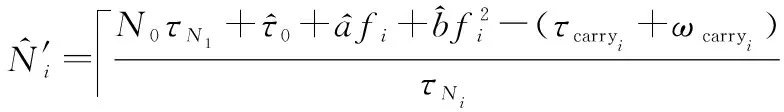
(16)

由于载波频率一般为千兆量级,其波长τNi(i=1,2,…,L)差别较小。以分段载波频率范围为例,其波长差异为0.002 3 ns,因此在|N0|≤4的范围内波长差异小于0.01 ns,因此可以得到近似关系如下:

(17)

此可以由式(16)和式(17)得到:

(18)

忽略载波相位测量误差,将式(18)代入式(6)可得

(19)

因此,遍历误差可以表示如下:

(20)

抛物线常数项系数只影响抛物线上下平移,而非常数项系数影响抛物线形状和变化趋势,因此相比于非常数项系数,其增加整周模糊度对遍历误差的影响可以忽略不计。因此,抛物线常数项系数并不影响非常数项系数的搜索固定结果。

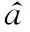
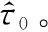
步骤 2固定第一段整周模糊度

步骤 3固定其余段整周模糊度

根据式(7)遍历并固定最小遍历误差对应的非常数项系数,得到分段群时延特性,再得到下一段群时延特性抛物线常数项系数。

按照上述算法遍历固定所有分段抛物线系数,得到所有分段群时延特性,最终得到通带群时延特性。

综上所述,基于频分多址信号载波相位的高精度导航接收机群时延测量技术具体测量步骤如下。

步骤 1码时延和载波相位测量

利用窄带扩频信号通过待侧通道测量得到各中心频点对应的码时延和载波相位。

步骤 2固定第一段群时延特性整周模糊度

通过遍历抛物线系数,计算遍历误差,固定最小遍历误差对应的抛物线系数,从而固定第一段群时延特性的整周模糊度,结合载波相位获得群时延特性。

步骤 3固定其余段群时延特性整周模糊度

利用前一段抛物线系数推倒得出下一段的常数项系数,遍历非常数项系数,通过计算遍历误差,固定最小遍历误差对应的抛物线非常数项系数,循环计算,最终得到通带群时延特性。

基于窄带扩频信号载波相位的高精度导航接收机群时延测量技术框图如图5所示。

3 仿真结果与分析

本节利用第2节提出的算法步骤进行仿真实验,通过与图2所示的真实群时延特性比对,对算法的准确性进行评估。

频分多址信号码率Δfc=0.5 MHz,假设待测通道的频率范围为[1 228.5 MHz,1 308.5 MHz],带宽为B=80 MHz。频分多址信号中窄带扩频信号数量N=160,窄带扩频信号的中心频率为

(21)

将频分多址信号送入待测接收机中得到的码时延通过真实群时延与方差为0.2 ns的加性高斯白噪声进行仿真模拟,仿真结果如图6所示。

将通带带宽分为N1=20段,每段8个群时延测量值,且每段的群时延特性满足抛物线特性。

根据仿真经验,二次函数的二次项系数取值范围为-0.2～0.2,遍历步长为0.002,一次项系数取值范围为-2～2,遍历步长为0.2。通过遍历二次函数系数寻找整周模糊度适配误差最小情况,以第一段群时延特性为例,遍历结果如图7所示。

可以看出，适配误差有3个明显的极小值,此时对应的抛物线二次项系数都为a=0.002,其剖面图如图8所示。

从图8中可以看出3个极小值对应的一次项系数分别为-1.82,-0.2,1.42。通过计算得到第一段码时延固定抛物线二次项系数后的一次项系数拟合结果为-0.12,因此取一次项系数为-0.2。根据式(5)和式(6)计算得出第一段相对群时延测量结果如图9所示。

搜索固定起点整周模糊度偏移量,对整周模糊度进行固定。第一段群时延特性常数项偏移整周模糊度后的遍历误差如图10所示。

从图10中可以看出,在常数项偏移两个整周模糊度时测量误差最小,常数项偏移两个整周模糊度后的第一段群时延测量结果如图11所示。

对剩余分段搜索固定抛物线非常数项系数后得到的群时延测量结果如图12所示。

可以看出,群时延测量结果与实际群时延基本一致,其测量误差如图13所示。群时延测量误差在皮秒量级,其产生的原因主要是载波相位测量误差,其精度较高,可以忽略不计。

4 实测验证

本文采用图4所示的设备连接方案,利用本文算法对两台高精度导航接收机的群时延特性进行测量,在零基线条件下,通过群时延矫正后得到的双频GLONASS实时动态(real-time kinematic, RTK)解算结果分析群时延测量算法的有效性。零基线设备连接图如图14所示。

测试环境位于某屋顶,两台接收机分别为天宝接收机和双模自研接收机,天线为自研天线。由于零基线测试需要对两台接收机使用相同的时钟源,因此采用10 MHz频标进行时钟同步。群时延矫正前RTK解算结果如图15所示。

从图15中可以明显看出，群时延矫正前精度较差,为分米量级。对通过基于载波相位的接收机群时延测量技术测量得到的群时延进行校正后,其RTK解算结果如图16所示。

可以看出校正后的RTK解算精度明显升高,达到毫米量级,由此可以验证群时延特性测量结果的准确性。

5 结 论

本文提出了一种基于窄带扩频信号载波相位的高精度导航接收机群时延测量技术,该方法在通道群时延特性为分段抛物线假设的前提下,利用窄带扩频信号的载波相位观测量遍历并固定分段抛物线系数,其遍历固定顺序为第一段抛物线非常数项系数、第一段抛物线常数项系数以及其余分段抛物线常数项系数。通过抛物线函数固定整周模糊度,结合载波相位反映各频点的群时延。

实验结果表明,该测量技术得到的群时延测量精度达到皮秒量级,满足GLONASS频分多址号载波相位的高精度应用的群时延测量需求。同时该方法的源信号为窄带扩频信号,实现简单方便,对导航接收机群时延具有良好的测量效果。