基于近程杂波协方差矩阵构造的俯仰滤波方法

林丽娜，郑文文，陆小凯，完 诚，钱乔龙

(1.海装装备项目管理中心，北京 100071；2.中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

对于机载相控阵雷达，引起杂波非平稳的因素主要有2个：一种为环境因素，例如地面起伏不平、比较强的杂散点和孤立干扰等因素；另一种为阵面因放置不同导致的非平稳，例如主杂波的多普勒随着距离的不同而变化导致非平稳性，这种非平稳性在非正侧面阵雷达中的表现尤为突出[1]。

对于二维面阵，在俯仰向的天线阵元具有区分来自不同俯仰方向回波的能力，即具有区分不同距离的回波信号的能力。依靠阵列天线俯仰向的阵元或俯仰向自由度可以分辨不同模糊距离的杂波[2]。

近程杂波距离近，衰减相对远距离杂波小，即使从俯仰方向图的副瓣进入，其杂波能量还是很强，从而极可能湮没远距离目标信号，导致目标检测性能下降。抑制近程杂波是为了提高杂波的距离平稳性，从而提高性能，最终提高目标信号的信杂噪比(SCNR)。对于非正侧阵的近程杂波抑制，常用的方法是谱补偿。通过谱补偿将近程杂波的距离非平稳性改善，但这类补偿只考虑了第1次距离模糊，而且很难保证目标增益不衰减。另外就是利用俯仰向自由度去做俯仰滤波，可分为2种：(1)俯仰向非自适应算法，需要精确知道雷达的参数，但是这种非自适应算法，受误差的影响比较大，尤其是受地形起伏和载机相对高度测量的误差影响比较大[3-5]；(2)俯仰向自适应算法[6-7]，通常训练样本中不可避免地存在远程杂波，所以近程杂波的抑制效果并不好，同时由于目标和远程杂波在很多情况下很难分开，所以目标有时会被衰减。

1 近程杂波特性

机载相控阵雷达在通常情况下脉冲重复频率比较高，存在距离模糊。杂波模型如图1所示，杂波组成主要有三部分，分别为方位主波束以及俯仰副瓣引入的近程杂波C1，主瓣杂波C2和俯仰主波束以及方位副瓣杂波C3，其对应的杂波协方差矩阵分别记为R1、R2和R3，具体关系如下[8]：

R=R1+R2+R3

(1)

图1 杂波模型

由俯仰副瓣引入的近程杂波C1是导致杂波非平稳的主要因素，定义来自第1次距离模糊的杂波为近程杂波。

图2是不同距离模糊杂波随模糊次数不同俯仰角的变化关系。从图2可以看出，近程杂波的俯仰角变化较快，远程杂波的俯仰角变化很小，而且俯仰角基本与俯仰主瓣角度保持一致。

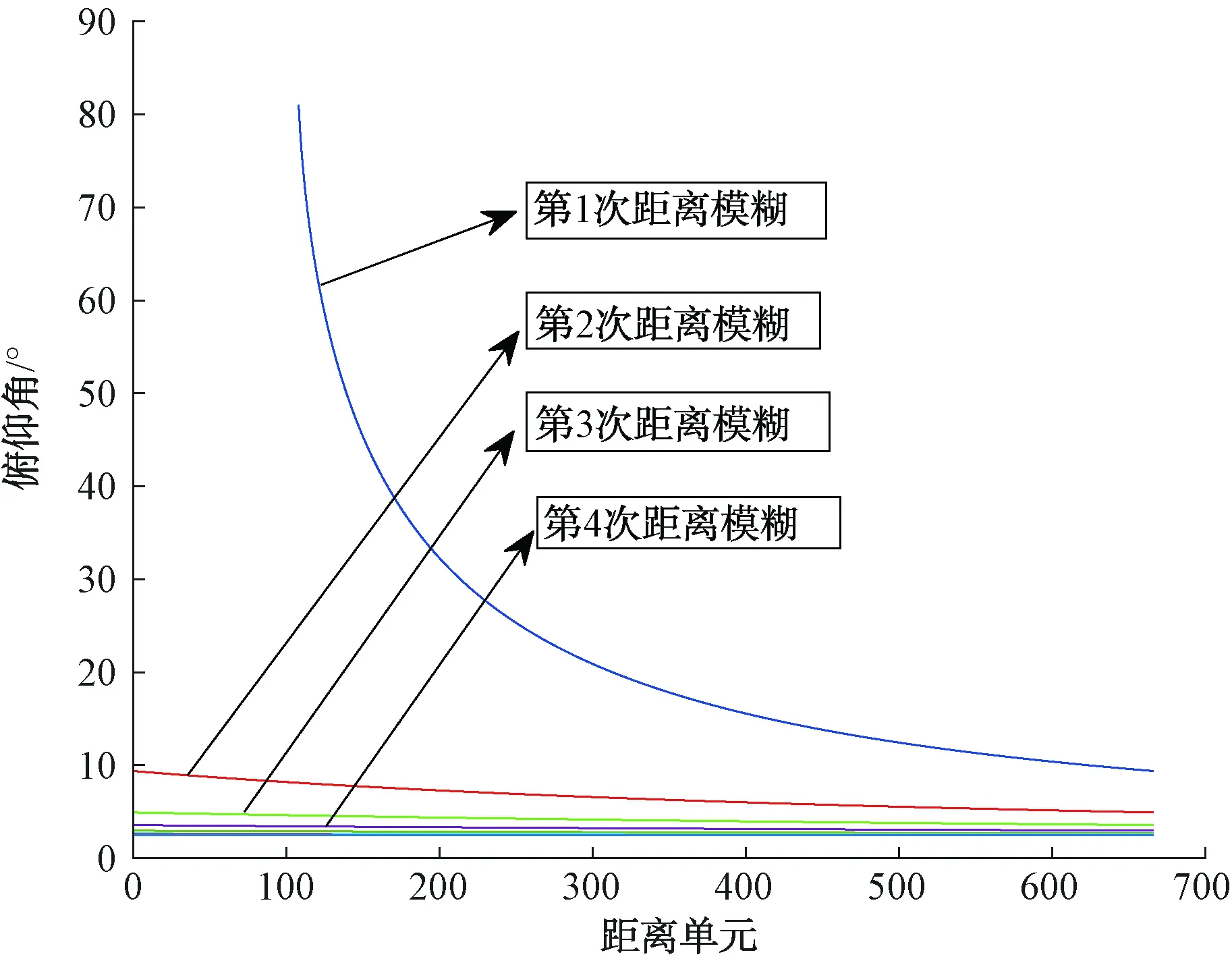
图2 不同距离模糊单元与俯仰角对应关系

其次，分析非正侧的距离多普勒关系。在计算第l个距离单元的俯仰角时，设其对应斜距为Rl，载机高度为H，地球曲率半径为Re，则俯仰角计算公式为：

(2)

所以杂波的距离与多普勒的关系表示为:

(3)

式中：α为载机速度与阵面的夹角；v为载机速度大小；λ为波长；θ为方位角。

图3是方位主杂波的距离多普勒变化关系，第1次距离模糊单元对应主杂波曲线如图3(a)中最左边的弯曲曲线，可见主杂波的多普勒随距离变化较大；而右边模糊次数较高的主杂波随距离变化不大，在图3(a)中用右边的竖线所示。将图3(a)放大后如图3(b)，每条曲线代表不同模糊时的距离多普勒关系。从图3(b)可以看出，远程的主杂波多普勒在一个很小的范围内变化，而且随着模糊次数的提高，越来越接近于1条竖线，多普勒几乎不随距离变化。

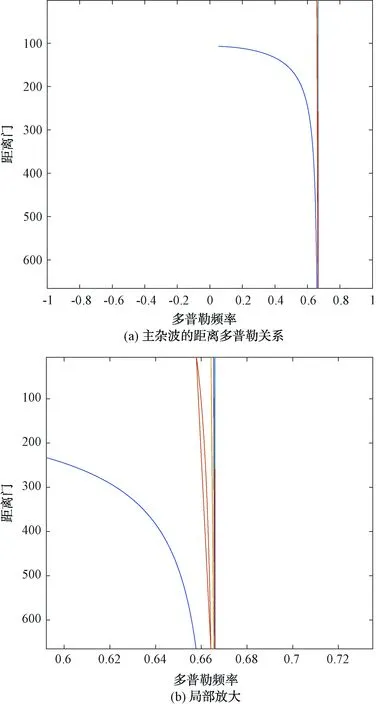
图3 前视阵的方位主波束的距离多普勒关系

地杂波的多普勒在远程随着距离变化较慢，而在近程随距离的变化比较快。虽然近程杂波是从天线的俯仰向旁瓣进入的，但是由于目前的超低副瓣技术难以实现，以及距离近、衰减小，在大多数情况下，功率往往与主瓣的远程杂波功率相当。这些近程杂波所引起的距离非平稳性会严重影响杂波的抑制性能。

综合上面两点分析，如果自适应训练的样本是这些不同分布的距离样本，那么就会使得自适应处理形成的凹口深度和方向与实际的不匹配，导致杂波抑制性能下降。

2 非平稳杂波抑制方法研究

主波束中心的俯仰角与远程杂波的俯仰角相差不大，而且远程杂波基本上都处于俯仰向主波束的范围之内。可以利用导向矢量构造协方差矩阵，选择俯仰向导向矢量处于近程杂波的构造协方差矩阵，这样使其凹口的位置可以对准近程杂波，而且近程杂波与远程杂波的俯仰角大小相差较大，所以不会引起主瓣畸变。

首先在计算近程杂波第l个距离单元对应的俯仰角φl附近取一系列间隔比较小的角度。然后，用匹配方法与待测样本进行匹配，留下匹配程度比较高的作为最终的训练样本，从而求出相应的加权系数，作为功率值，以此估计近程杂波协方差。

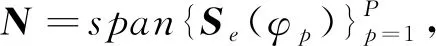
(4)

式中：αp代表复幅度，那么近程杂波的协方差矩阵可以表示为：

(5)

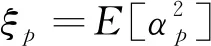
(6)

上式是一个凸优化问题，直接给出该办法的具体步骤:

(1) 初始化

p=1,2,…,P

(7)

(2) 估计协方差矩阵

(8)

(3) 更新ξp

(9)

式中：p=1,2,…,P。

(4) 重复步骤(2)和步骤(3)K次。

由步骤(1)可以得到某个俯仰角对应俯仰导向矢量与样本匹配最好，这样相当于得到了该近程杂波对应的俯仰角，虽然可能有一定的误差，但在可接受的范围内。所以在高度有误差时，也可以得到比较好的近程抑制效果。

假设俯仰向阵元个数为M，目标俯仰角为φt，阵元间距为d，则目标俯仰导向矢量为：

(10)

考虑到主波束俯仰角与大多数模糊距离单元俯仰角之间的间隔较小，为避免形成俯仰凹口导致主瓣畸变，俯仰自适应波束形成公式定义如下：

(11)

3 仿真实验

实验具体的参数如表1所示，采用8×16的前视面阵。在阵面法线方向加入归一化多普勒频率为0.150 6、距离为60 km的动目标。将俯仰向阵元直接合成，距离多普勒谱如图4所示，根据动目标的归一化多普勒频率和距离可以计算出它所对应的多普勒通道数为42，距离单元数为128，而在该位置处由于近程杂波比较强，动目标被湮没，难以被检测出来。通过本文的方法，弯曲的近程杂波不但得到较好的抑制，而且湮没的动目标也显现出来了，如图5所示。

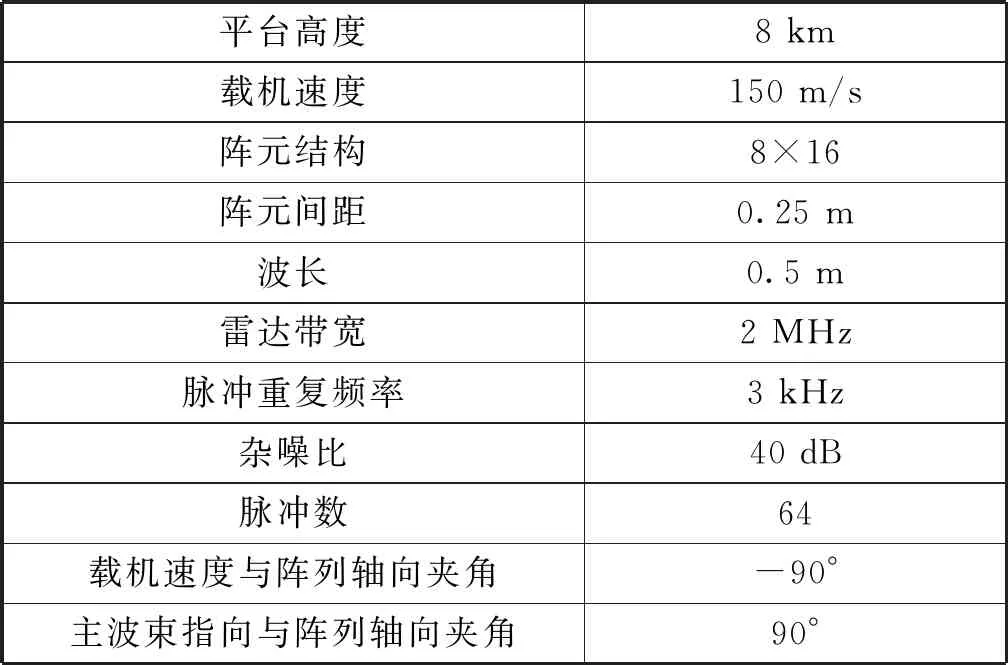
表1 前视阵雷达仿真参数

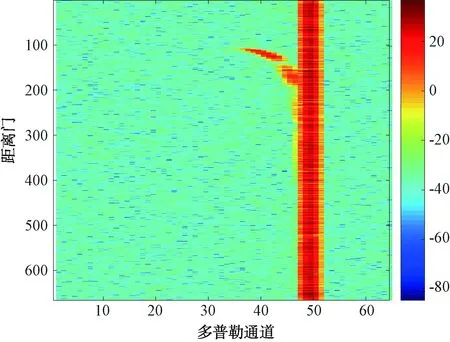
图4 直接进行俯仰向阵元合成的脉冲多普勒处理

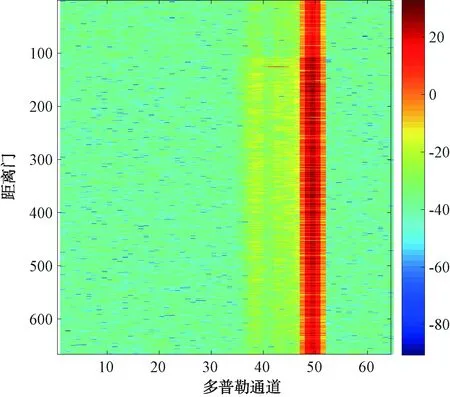
图5 本文方法进行合成的PD处理

图6是常规俯仰向阵元合成和本文俯仰向滤波的脉冲多普勒PD处理结果，可以看出2种方法对主瓣杂波的抑制效果差不多。本文所提方法能够有效抑制近程杂波且保证目标衰减小，相比俯仰向阵元合成方法，近程杂波被抑制最多达到18 dB。

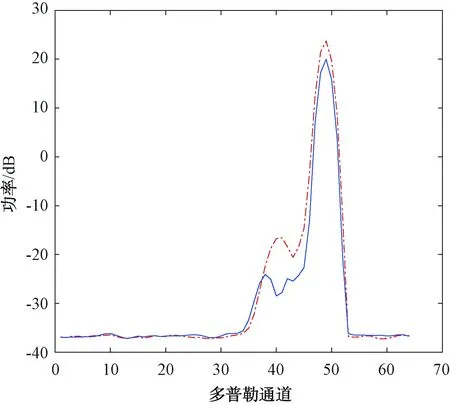
图6 杂波剩余功率对比

图7画出了在所加目标附近杂波的功率，以验证近程杂波对目标检测性能的影响。从图6可以看出，俯仰向阵元直接合成在所加目标附近杂波功率比较强，容易引起虚警，不利于目标检测。而用本文方法则目标功率与周围杂波功率很容易区分，对检测目标特别有利。

通过本文方法，近程杂波所引起的杂波非平稳性得到很大减弱。后续用训练样本去估计协方差矩阵就能较好地反映待检测单元的杂波和噪声的特性，再做STAP处理就能尽可能多地抑制剩余杂波。图8就是经过俯仰向阵元合成的EFA(也叫3DT，扩展因子化方法)处理结果，从图中可以看出弯曲的近程杂波还是很强，由于杂波的非平稳，导致处理完主瓣杂波还是很强。图9就是经过本文方法先在俯仰向进行滤波，杂波的非平稳性减弱，然后进行EFA处理，主瓣杂波得到很好的抑制。

图9 俯仰向经本文方法滤波后EFA处理

4 结束语

本文针对机载雷达的杂波非平稳问题展开了研究，给出了一种非平稳杂波抑制方法。传统的非平稳杂波抑制方法一般采用多普勒补偿的方法，但此类方法在有误差的情况下效果会变得很差，而且补偿后目标会有损失。如果只是在俯仰向进行阵元合成，近程杂波还会有大量剩余，一旦目标落入近程杂波区域，目标就有可能被湮没而无法检测。本文方法在计算出近程杂波的俯仰角之后，得到能够表示近程杂波的矢量空间，然后构造出协方差矩阵，求解出匹配最好的加权系数，尽可能表征近程杂波的特性，然后通过俯仰空域滤波从而滤掉近程杂波。杂波的平稳性得到改善后，后续的STAP处理可以较好地抑制远程杂波。