万米级深海陶瓷耐压结构水下内爆流场数值模拟

陈锋华，赵 敏

(上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室，上海 200240)

深海资源极其丰富，水下潜器是探测深海的重要装备。其中，耐压结构作为潜器的核心部件，为潜器内部非耐压系统设备的正常工作提供保护。陶瓷材料强度高，密度小，耐磨损，无磁性，将其作为耐压结构材料能大大提高潜器的性能。但是，中空的陶瓷耐压结构在深海高压环境中面临着内爆的风险。内爆是爆炸的对立面，是指由于外部压力高，内部压力低，耐压结构向内塌陷。在深海环境下工作的耐压结构，外表面承受高静水压力载荷，当耐压壳在外载荷作用下发生屈服或者屈曲时，壳体会被压溃，随后塌陷，流场静水压力转化为流体动能，水流压缩结构及其内部气腔至最小限度后，内部气体会向外反弹，并向流场中传递冲击波。

水下内爆产生的冲击波压力极大，远大于环境压力，一旦超过周围结构的强度极限，就会使周围结构压溃。因此，深海耐压结构的内爆可能会造成连锁内爆反应，该过程被称为“殉爆”或者“链式内爆”。图1所示的美国“海神号”潜器在下潜到水下9 990 m左右时，由于陶瓷耐压结构发生内爆，产生了巨大的冲击波，随即引发殉爆，最后导致整个潜器成为碎片[1]。

图1 “海神号”潜器及其陶瓷球型耐压结构

在超高压条件下，陶瓷耐压结构由于其脆性材料特性，一旦发生内爆，会直接被压溃成粉末状，而不存在与金属结构类似的大变形吸收能量现象。图2展示了陶瓷耐压结构及其内爆后所形成的粉末，可见内爆对陶瓷结构的损毁十分彻底，形成粉末状残骸，耐压壳流固耦合现象不明显，内爆能量主要由流场形成的冲击波向外传递。

图2 单个陶瓷耐压结构及其内爆后形成的粉末

中空的陶瓷耐压结构被压溃后，其内部气腔的压缩—反弹现象与气泡溃灭相似。Rayleigh[2]于1917年对气泡溃灭问题进行了研究，提出了球形气泡溃灭理论，用于描述单个气泡在不可压缩、无黏流动中的生长和溃灭。Plesset[3]在此基础上考虑液体的黏度和表面张力的影响，推导出气泡半径随时间变化的二阶非线性常微分方程，即Rayleigh-Plesset方程。Keller等[4]考虑了液体的可压缩性，提出更准确地描述气泡运动的Keller-Miksis方程。气泡运动理论主要针对水下爆炸等产生的气泡，当其内部为高压时则气泡膨胀，当其内部气压低于静水压时则压缩，如此反复形成脉动。而耐压结构的内爆则是结构压溃后静水压对内部初始的低压气腔做功，水的动能不断增大。此外，耐压结构的尺寸远大于气泡，气泡运动关注内部气体的变化，耐压结构内爆更关注冲击波在周围液体中的传播。

Turner[5]使用中空玻璃耐压结构在6.996 MPa的压力筒中进行水下内爆试验，得到了冲击波压力曲线，并使用DYSMAS软件对该试验进行了数值模拟，指出不考虑容器外壳会使得内爆模拟的冲击波压力偏大。Morenko[6]针对Turner的试验，基于流体体积法(VOF)，使用OpenFOAM软件对耐压结构内爆进行了不带壳体结构的纯流体模拟，指出增大气腔内部气压能有效降低内爆的强度；球体半径越大则内爆产生的压力峰值越大。Farhat等[7]对小型柱体金属壳进行内爆试验，指出其内爆压力脉冲受屈曲模式和失效位置影响。杜志鹏等[8]基于能量守恒原理，推导出一种不可压缩流体中球型容器内爆理论模型，探究了冲击波压力与初始压力、球体半径的关系。Chamberlin等[9]提出了一种基于能量的度量标准，将水下耐压结构内爆的能量划分为：系统中的初始能量(势能)，作为压力脉冲释放到流体中的能量，由内爆结构吸收的能量，以及由滞留在内爆结构内的空气吸收的能量。黄治新等[10]根据应力波原理，提出一种水下中空结构物内爆试验方法，并对0.5 MPa压力下的光电倍增管内爆进行了试验。张晓龙等[11]通过有限元仿真分析了耐压结构在内爆临界状态的失效过程，指出耐压结构失效的主要原因是内表面的局部拉应力过大。

以往对水下内爆的研究主要集中在气泡溃灭等小尺度对象上，以及低压环境、液体不可压缩的耐压结构问题中，对适用万米级深海潜器陶瓷耐压结构的超高压、液体可压缩的内爆研究较少。文中基于针对可压缩多相流问题开发的开源代码ECOGEN[12]，采用直接数值模拟方法，应用自适应直角网格，对6.996 MPa 压力下半径为3.81 cm的耐压结构进行内爆模拟，通过与理论解和试验值的对比，验证了方法的可行性和准确性，并分析了流场压力波动特性。在此基础上，对万米级深海(115 MPa压力)陶瓷耐压结构进行内爆模拟，分析了其形态演化及冲击波特性，模拟并分析了不同半径对耐压结构内爆冲击波特性的影响。

1 流场数值模拟的计算方法

1.1 可压缩多相流Kapila五方程模型

深海耐压结构内爆的数值模拟涉及到水和空气两相，且在万米级超高压环境下，水被认为是可压缩流体，因此使用可压缩多相流模型来模拟该问题更为准确。Kapila五方程模型被广泛用来模拟可压缩多相流[13]。该模型假设两相间速度和压力始终保持连续，是七方程模型[14]的简化。该假设是基于在大多数的两相流问题中，两相达到速度平衡和压力平衡的特征时间极短。式(1)为Kapila五方程模型的具体形式，其中包括体积分数的发展方程、两相的连续性方程、混合物的动量方程和能量方程。

(1)

其中，下标1、2分别代表两相，αk表示k相的体积分数，ρk表示k相的密度，u表示两相的混合速度，P表示两相的混合压力，ρ表示两相的混合密度:

ρ=α1ρ1+α2ρ2

(2)

E表示两相的总能量：

E=U+0.5||u||2

(3)

其中，U表示两相的总内能：

U=Y1U1(ρ1,P)+Y2U2(ρ2,P)

(4)

其中，Yk表示第k相的质量分数，其定义为：

(5)

(6)

其中，ck表示k相的声速，而混合物的声速表示为:

(7)

1.2 状态方程

文中气体使用理想气体状态方程，如式(8)所示：

pV=nRT

(8)

其中，p表示压强，V表示体积，n表示摩尔数，R表示普适气体常数，T表示温度。

在常规压力下，水通常被认为是不可压缩流体。而万米级深海潜器耐压结构的内爆是一个强冲击、超高压问题，水在该环境下是可压缩流体。文中水的状态方程使用刚性气体方程[15]，该方程能很好描述液体在高压下的状态，已被广泛应用于声致发光、声震碎石、水下核爆炸等领域。刚性气体方程的形式如式(9)所示。式(10)为声速计算公式。

p=(γ-1)ρe-γP∞

(9)

(10)

其中，γ为热容比；e是单位质量的内能；P∞是压力常数，当P∞=0时，则刚性气体方程变成了理想气体方程，可见理想气体方程是刚性气体方程的一种特殊形式。

求解式(4)可以得到混合压力P，在气相和液相分别使用上述状态方程的基础上，则混合物状态方程可写为式(11)，其中下标1表示液相，下标2表示气相。

(11)

数值模拟使用为解决可压缩多相流问题而开发的基于C++的开源代码ECOGEN，该代码集成了多种数学模型，其可行性与准确性已在多种物理问题上得到验证，如气泡溃灭、激波管、激波冲击氦气泡、水滴雾化、表面张力问题等[12,16-17]。

2 算例配置与网格收敛性验证

2.1 算例配置

陶瓷耐压结构在深海中发生内爆，其破碎时间极短，可认为是瞬间破碎，且内爆后呈粉末状。为简化内爆的复杂过程，并保留其关键物理特征，文中用相同尺寸的球体气腔代替球型耐压结构，进行流场数值模拟。Morenko[6]指出对不带壳体结构的内爆流场特性的研究，将为壳体的设计建造提供重要支持，对规避内爆危害具有重要意义。同时，内爆的流场数值模拟还能提供详细的全流场信息，能有效弥补试验中数据较少的缺陷。

球体可由半圆形以其直径为轴而旋转得到，因此单个球型耐压结构内爆的数值模拟可使用二维轴对称模型进行模拟，有效提高了计算效率和模拟精度。

首先以Turner[5]的试验为对照，对6.996 MPa的内爆问题进行模拟。该问题的研究对象是半径为3.81 cm 的玻璃球，并在距离球心10.16 cm的地方设置监测点以监测内爆过程中的压力波动。玻璃同样是脆性材料，内爆后流固耦合现象不明显，因此仍用相同尺寸的球体气腔代替球型耐压结构。如图3所示，该算例的计算域为方形区域，大小为半径的10倍；球心位于计算域原点，球体侧的两个边界分别设置为轴对称边界和对称边界，其他边界设置为无反射边界。在数值模拟中，无反射边界条件用于避免在进口和出口边界处产生不真实的非物理性反射，能使得计算流场不受远场边界的位置影响，从而使得计算结果更准确。此外，使用该条件可把计算域设置得更小，从而能提高计算效率。在深海内爆的流场数值模拟中，无反射边界条件能有效模拟深海中的无限海域压力条件，并能有效消除边界形状对模拟的影响。为有效捕捉内爆过程中球体形状变化，以及膨胀波、压缩波的传递，并提高模拟的精确性，该模拟在均匀的直角网格基础上使用如图4所示的3层自适应加密网格，在大压力梯度和大密度梯度等关键区域进行自适应加密[18]。计算的初始条件为：内部设置为理想气体，压强为0.1 MPa；水的初始压强为6.996 MPa；计算域的初始速度均为0。在刚性气体方程中，水的热容比γ=4.4，压力常数P∞=6×108；在理想气体方程中，空气的热容比γ=1.4。

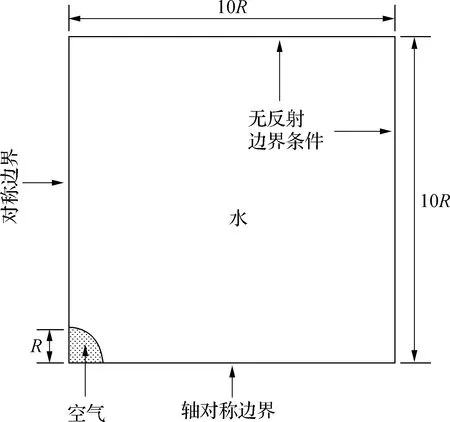
图3 单个球型耐压结构内爆的计算域示意

图4 自适应直角网格

在验证了方法的可行性后，进行了万米级深海陶瓷耐压结构内爆的流场数值模拟。该算例同样使用与上述相同的二维轴对称模型来模拟三维问题。球体半径为5 cm，水的初始压力为115 MPa，其余条件与上述算例的设置保持一致。

2.2 网格收敛性验证

以6.996 MPa压力下单个球型耐压结构内爆为考察对象，背景网格分别使用200×200，400×400和800×800三套网格，进行网格收敛性验证。表1为距离球心10.16 cm处监测点压力峰值和气腔溃灭时间的网格收敛性验证结果。可见，压力峰值和溃灭时间的收敛比率均小于1，符合收敛性准则[19]。考虑计算效率，后续计算使用400×400的背景网格。

表1 监测点压力峰值和气腔溃灭时间的网格收敛性验证

3 球型脆性材料耐压结构内爆的数值模拟结果验证与分析

3.1 6.996 MPa压力下球型玻璃材质耐压结构内爆的半径演化验证

在气泡溃灭理论中，Keller-Miksis(K-M)方程在Rayleigh-Plesset方程的基础上考虑了水的可压缩性等因素[4]，已被普遍认可，可用于验证球体内爆后的半径演化。文中使用式(12)形式的K-M方程：

(12)

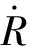
使用龙格—库塔法求解上述方程，可以得到球体半径随时间的变化曲线。将其与数值模拟中的半径变化曲线进行比较可验证数值模拟的准确性。

在算例中，如式(13)所示，通过计算每一个计算单元的体积和气体体积分数的和得到气体的体积，并假设该体积是标准球体的体积，运用球体体积公式(14)可计算出球体在每一时刻的半径大小。

(13)

其中，n表示网格单元的总数，αg,i和Vc,i分别表示每个网格单元i的气体体积分数和体积。

(14)

图5是6.996 MPa压力下耐压结构内爆后气腔半径演化的计算流体力学(CFD)数值模拟结果和K-M方程的理论解结果的比较。理论解以及数值模拟结果均显示在该环境压力下，半径为3.81 cm的球型气体空腔内爆存在明显的多次压缩—反弹现象，其中第一次压缩与第一次反弹阶段的曲线吻合度极高，后续阶段曲线的趋势也较为吻合。

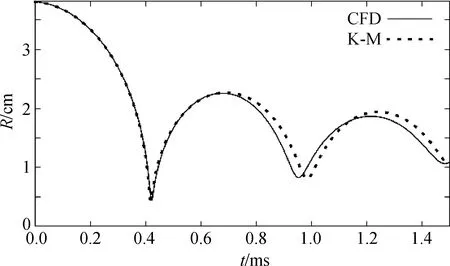
图5 6.996 MPa下球体半径演化曲线

如表2所示，6.996 MPa压力下球型耐压结构气腔半径演化的数值模拟结果和K-M理论解在溃灭半径、溃灭时间、反弹最大半径和首次反弹结束时间上均吻合良好，有效验证了模拟的准确性。

表2 6.996 MPa下半径演化模拟结果与K-M理论解对比

图6显示了6.996 MPa压力下单个球体耐压结构内爆的流场体积分数变化，深色区域表示气相、浅色区域表示液相。由图6可见，内爆发生初始阶段，低压的气体空腔受到深海液相高压而压缩，因受力均匀，气腔仍保持较规则球体形状。气腔内部为理想气体，体积降低导致压力增大，当气腔界面内外压强相等时，气腔由于惯性继续向内压缩。球型气腔在第一次压缩到最小体积后，因内部压力远大于环境压力，进入反弹阶段。反弹到一定阶段后，气腔内外压强再次达到平衡，气腔由于惯性继续向外反弹。当气腔界面速度达到0后，由于内外压差的存在，气腔再次开始反弹，如此循环，经过多次压缩—反弹过程后，最终气腔内外压力达到平衡，且界面速度为0，气腔体积不再发生变化。

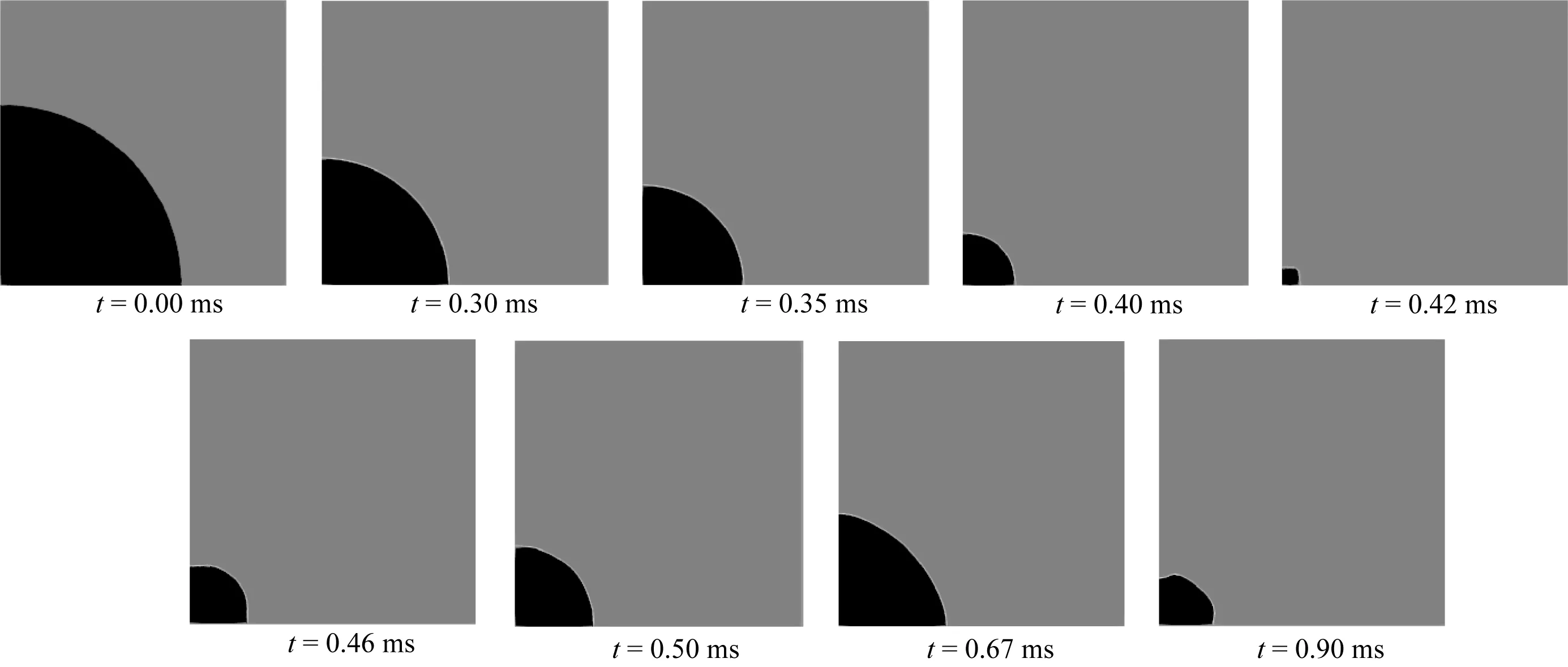
图6 6.996 MPa压力下体积分数变化

3.2 6.996 MPa压力下球型玻璃材质耐压结构内爆的冲击波压力结果验证与分析

图7是距离球心10.16 cm处的监测点上压力变化曲线，该监测点在耐压结构表面以外。

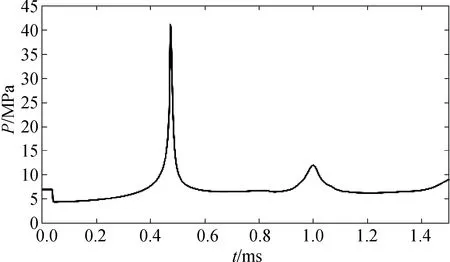
图7 6.996 MPa下距离球心10.16 cm处的压力变化曲线

由图7可见，内爆初始时刻，监测点处压力保持环境压力不变，在0.037 ms后，该处发生急剧压降，压力从环境压力6.996 MPa快速下降到4.405 MPa，下降幅度为37%。随后，该监测点处压力缓慢升高，于0.37 ms秒恢复到6.996 MPa。此后，监测点压力在短时间内急剧上升，于0.47 ms达到峰值41.1 MPa，并于其后迅速下降。此后该处压力仍出现多个周期性峰值，且峰值逐渐降低，并远低于第一个压力峰值。

距离球心10.16 cm处监测点的数据显示，该处捕捉到的压力峰值为41.1 MPa，Turner[5]的流体数值模拟结果为38.4 MPa，二者吻合良好。此外，Turner的试验结果显示，在考虑球体玻璃外壳时，监测点的压力峰值为31.1 MPa，该结果比纯流体计算结果偏小，主要原因在于玻璃结构在内爆中的压碎过程吸收了部分能量，而纯流体模拟中缺少这一过程，因此反弹压力较大。总体上看，该模拟计算结果可信，文中所用方法能较好模拟该问题。

在耐压结构气腔压缩阶段，球型气腔向外传递膨胀波，膨胀波经过之处当地环境压力快速下降。图8展示了膨胀波向外传递阶段的压力云图。

图8 6.996 MPa下膨胀波传递阶段压力云图

在气腔体积被压缩到最小后，气腔内部压力已远高于环境压力，球体气腔开始向外传递压缩波，压缩波的传递使得其所经过区域压力急剧上升。图9为6.996 MPa压力下球型耐压结构内爆压缩波传递阶段的压力云图。

3.3 115 MPa压力下球型陶瓷耐压结构内爆的半径演化验证

图10是115 MPa下半径为5 cm的球型陶瓷耐压结构内爆的半径演化数值模拟结果和K-M方程结果的比较。模拟结果输出的半径曲线在压缩阶段与K-M方程较为吻合。K-M方程结果显示，球体气腔半径在0.124 ms时压缩到最小值0.287 cm；数值模拟中，球体气腔半径在0.123 ms时压缩到最小值0.288 cm。数值模拟和理论结果的时间误差为0.8%，最小半径误差为0.3%。反弹阶段的半径曲线较为平缓，后续波动中，数值模拟结果不如K-M方程的曲线明显，主要原因在于K-M方程的推导建立在界面马赫数较小的基础上[12]，而该算例在压缩阶段后期的马赫数达到了1.1以上。总体上看，数值模拟结果与K-M方程理论解吻合良好，有效验证了模拟的准确性。

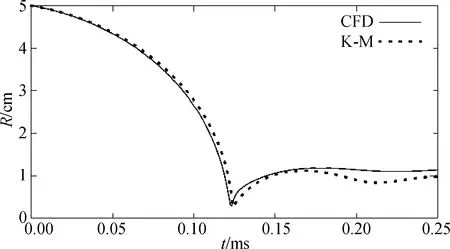
图10 115 MPa下球体半径演化曲线

将115 MPa和6.996 MPa的计算结果进行比较，可以发现，在内部气体的初始压力均为0.1 MPa的前提下，115 MPa的单球内爆在压缩到最小体积之后的反弹明显较弱。主要原因是要使115 MPa环境压力的海水产生与6.996 MPa压力下同样规模的动能，其所需能量远大于该压力下内爆所产生的能量。

3.4 115 MPa压力下球型陶瓷耐压结构内爆的冲击波压力结果分析

图11展示了在115 MPa压力下半径为5 cm的球型陶瓷耐压结构内爆过程中球体外不同监测点的压力变化曲线，图中的距离表示从球心到监测点的距离。在压缩阶段，由于外域海水向气腔内流动，从气腔向外传递膨胀波，导致球体外部在内爆的初始阶段产生压降。距离耐压结构球面越近，则越早产生压降，压降的幅度从球面向外越来越小，且压降的变化幅度随着到球面距离的增加而越来越平缓。在距离球心6 cm的监测点上压力从115 MPa的环境压力降到了19 MPa，降低幅度达到83.5%；在距离球心16 cm的监测点上压力则降低到了80.2 MPa，降低幅度为30.3%；在距离球心26 cm的监测点上压力则降低到了93.8 MPa，降低幅度为18.4%。

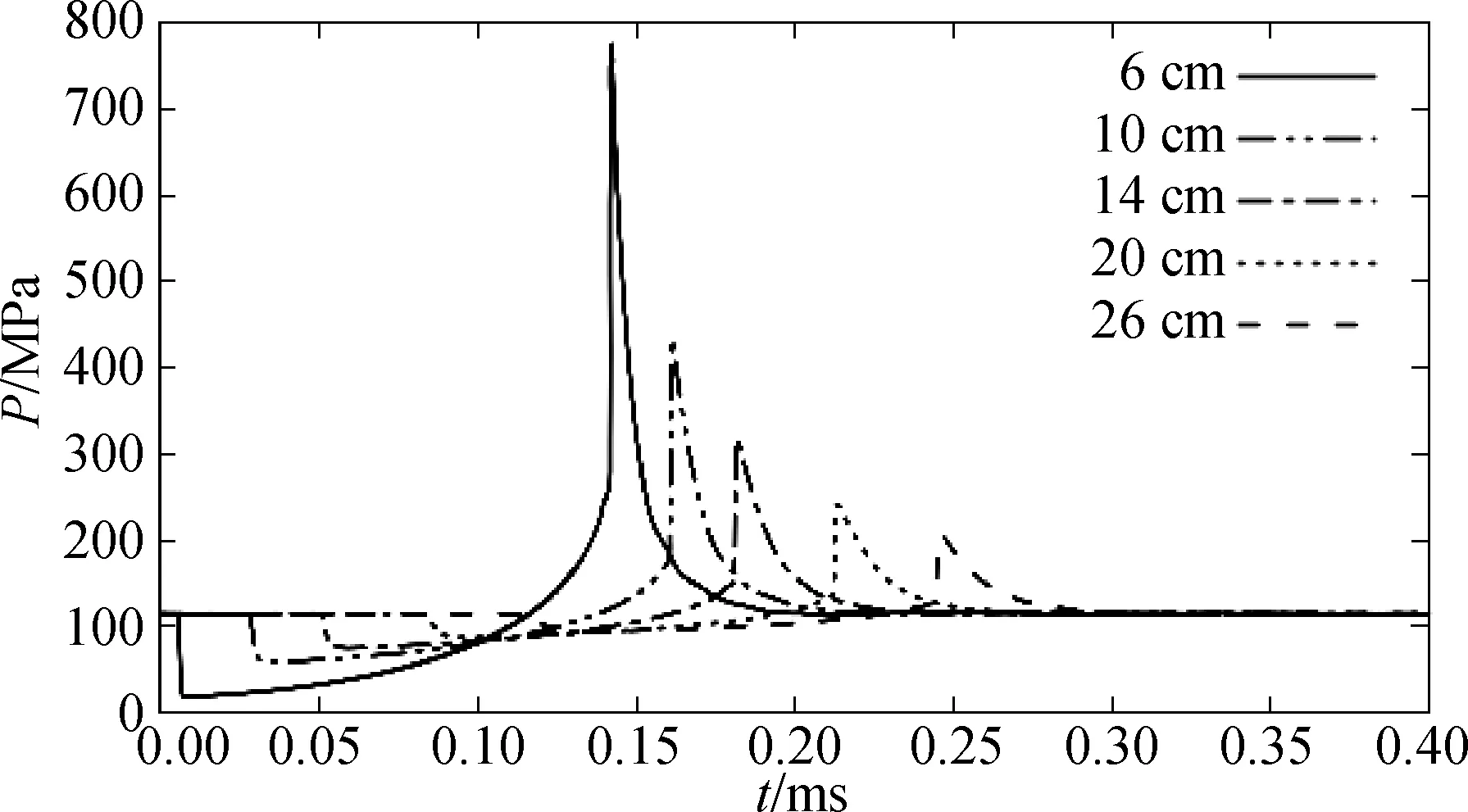
图11 115 MPa下球体外不同监测点的压力变化曲线

球体外部监测点的压降持续时间非常短暂，压力在到达最低点后开始逐渐升高。在0.123 ms气体空腔的体积被压缩到最小，其压力急剧增加，并迅速向外传递压缩波，导致球体外部监测点的压力快速增加。表3为到球心距离不同的监测点的冲击波压力峰值。在距离球心6 cm的监测点上压力峰值达到了774 MPa，约为环境初始压力的6.7倍；在距离球心16 cm的监测点上压力峰值达到了284 MPa，约为环境初始压力的2.5倍；在距离球心26 cm的监测点上压力峰值达到了205 MPa，约为环境初始压力的1.8倍。

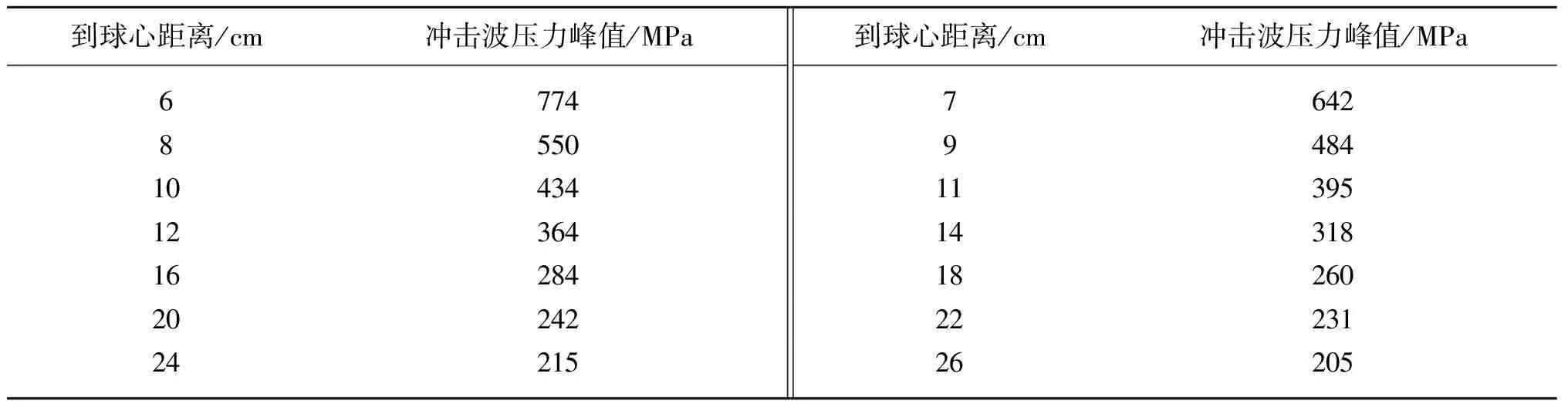
表3 到球心距离不同的监测点冲击波压力峰值

通过分析以上数据，发现可用负指数幂函数来拟合球体外部某点处的压力峰值与该点到球心距离的关系，如式(15)所示，冲击波衰减系数为-1.343，R2为0.999 4。图12为冲击波压力峰值与监测点位置关系曲线。根据拟合公式，可以预测，在距离球心100 cm的监测点处由内爆产生的压力峰值为129.6 MPa，而在距离球心200 cm处监测点的压力峰值则为120.8 MPa。可见，这两处的压力峰值仅相差6.8%，压力变化已趋于平缓，球体内爆所产生的压力波对该范围的水域影响较小。

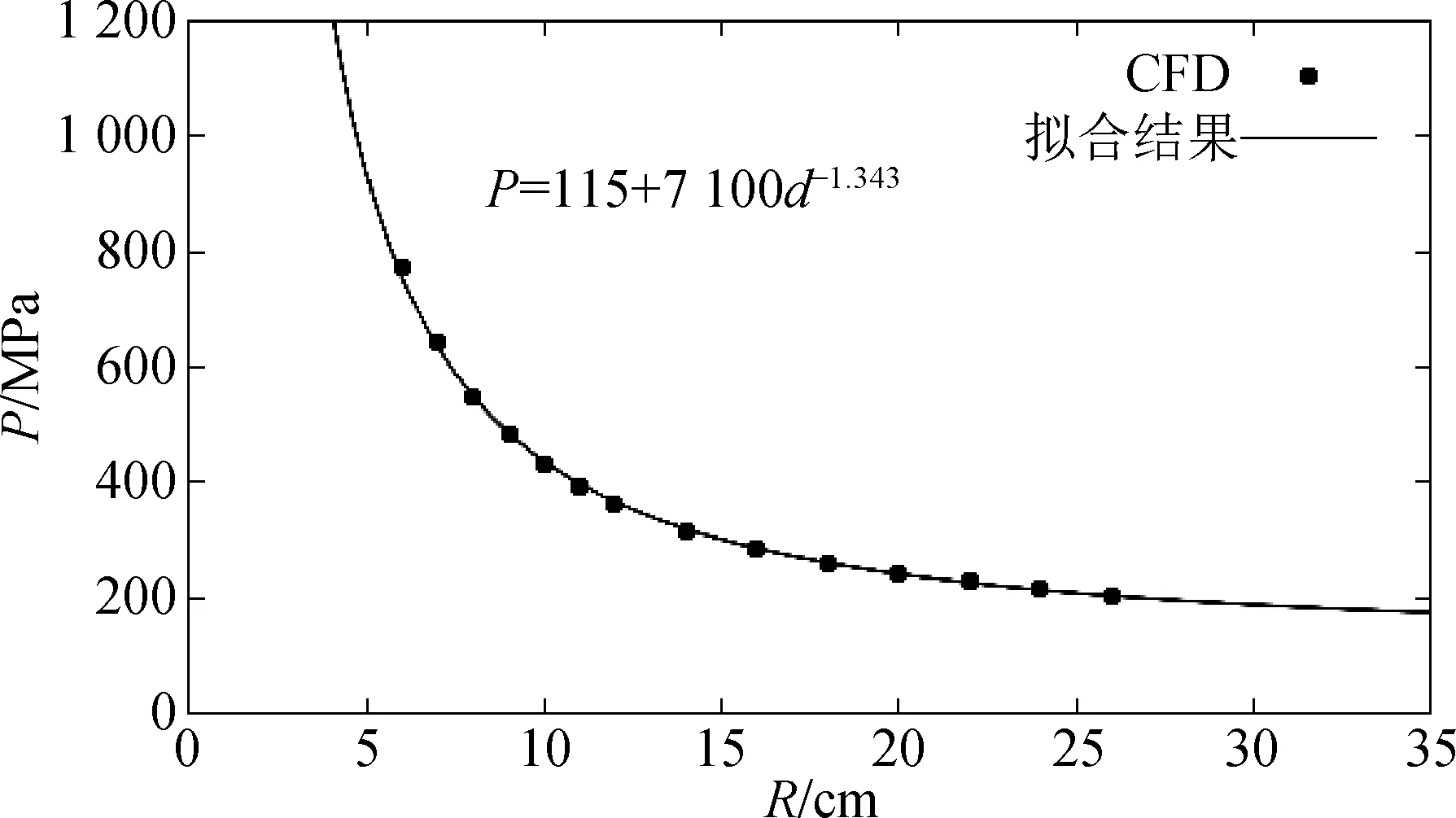
图12 压力峰值与监测点位置关系曲线

P=115+7 100d-1.343

(15)

以各监测点上的压力峰值为参考点，记录耐压结构内爆后所产生的冲击波到达各监测点的时间，再算出相邻监测点之间的距离，求得每两个相邻监测点之间的平均冲击波传播速度。图13展示了冲击波在球型耐压结构外的传播速度随距离的变化曲线。在距离球心6.5 cm处，冲击波的传播速度达到2 174 m/s；在距离球心15 cm处，冲击波的传播速度达到1 886 m/s；在距离球心25 cm处，冲击波的传播速度达到1 835 m/s。可见，在115 MPa环境下耐压结构内爆后产生的冲击波传播速度极大，与该环境下的声速接近，且随着传播距离的增大，冲击波速度整体呈缓慢下降趋势。

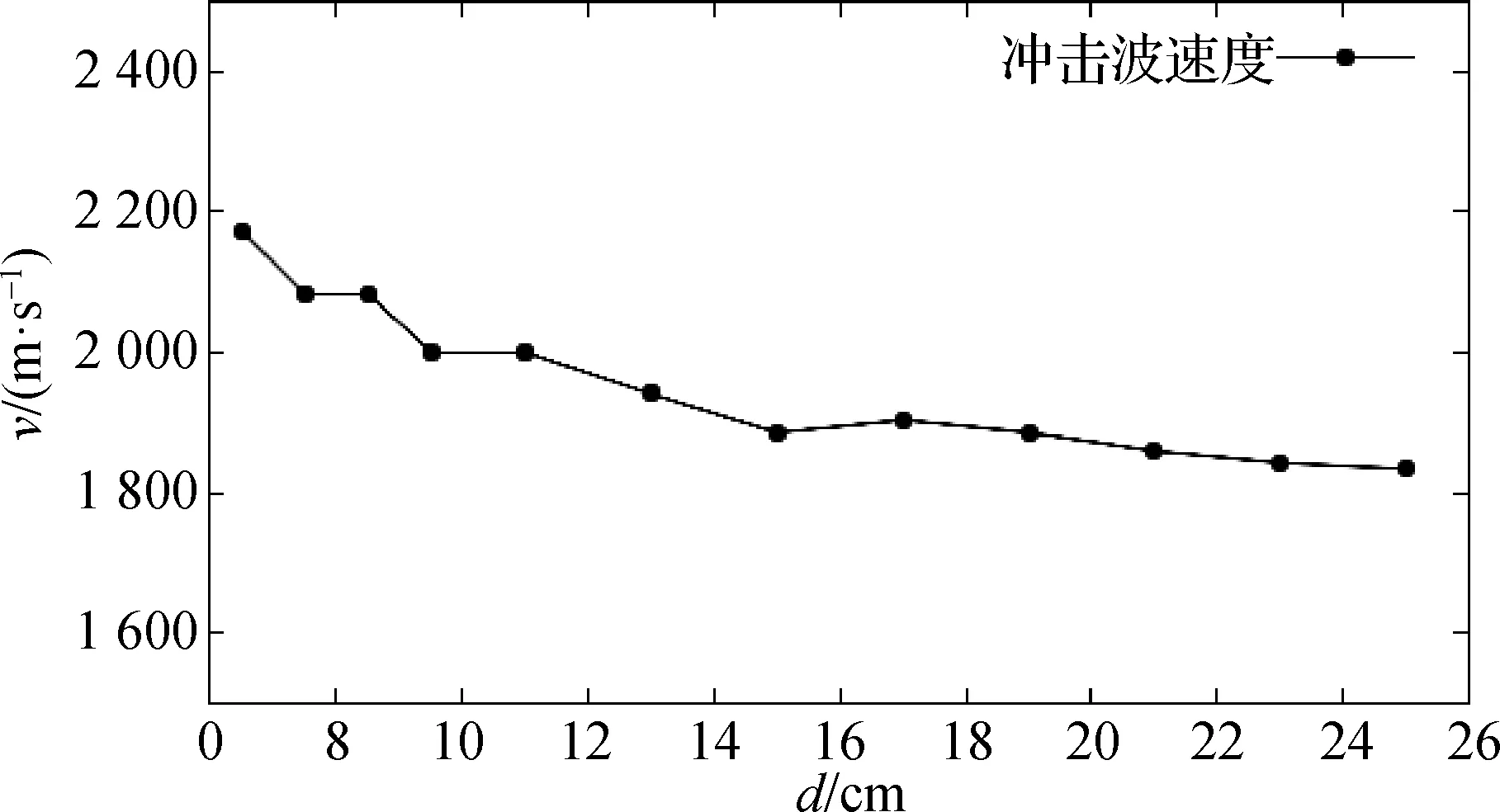
图13 冲击波在球体外的传播速度随距离变化曲线

3.5 不同半径球型陶瓷耐压结构内爆的冲击波压力特性

为研究在115 MPa的压力下不同半径的球型耐压结构内爆规律变化，这里在进行了半径为5 cm的耐压结构内爆模拟后，还分别对半径为1、3、7和9 cm的耐压结构进行了内爆模拟。图14展示了不同半径的球体在距离球心10 cm处监测点的压力峰值，并根据模拟值给出了拟合公式。由图14可见，在距离球心10 cm 处，半径为1、3、5、7和9 cm的球体内爆冲击波峰值分别为154.8、276.3、433.9、625.1和844.3 MPa。

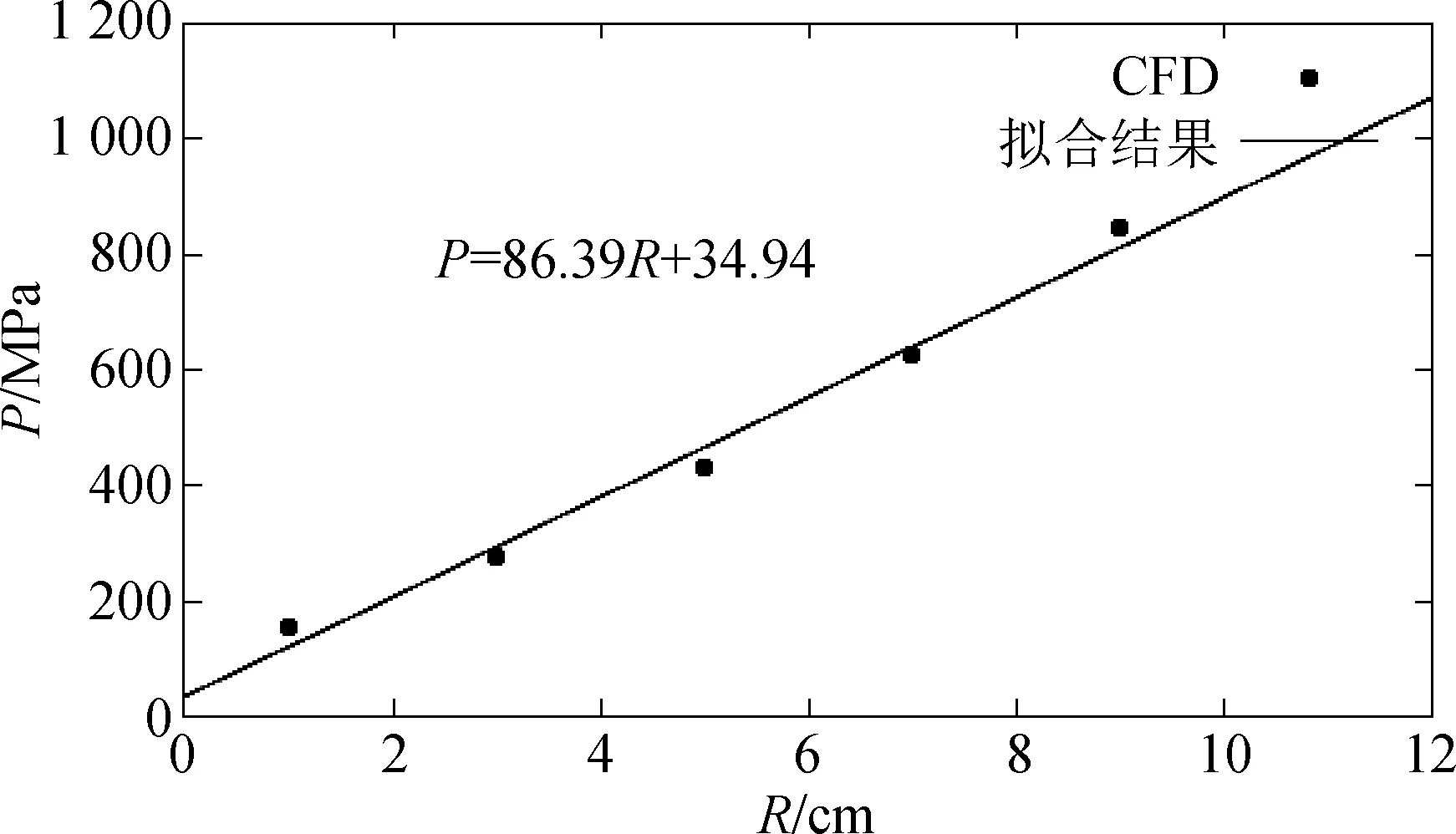
图14 不同半径的球型耐压结构内爆后在距离球心10 cm处的压力峰值

可见监测点上的压力峰值与球体半径接近正比例关系，拟合公式为：

P=86.39R+34.93

(16)

由该式可得，在115 MPa压力下发生内爆的球型耐压结构半径每增加1 cm，在距离球心10 cm处的监测点压力峰值增加约86 MPa。

4 结 语

基于针对可压缩多相流问题开发的开源代码ECOGEN，使用直接数值模拟，采用自适应直角网格，对深海潜器陶瓷耐压结构的水下内爆进行了数值模拟，通过收敛性分析，并将模拟结果与理论解和试验值进行比较，验证了模型计算的准确性。在此基础上对万米级深海压力下的球型陶瓷耐压结构内爆进行数值模拟。得出的主要结论如下：

1)深海潜器陶瓷耐压结构发生内爆后，其内部气腔存在多次压缩—反弹现象，环境压力越大则反弹越不明显。

2)在内爆后的压缩阶段，海水涌进耐压结构内部气腔，外部流场产生压降；在反弹阶段，气腔向海域传递冲击波，流场压力急剧增加。冲击波传递速度与声速接近。

3)半径为5 cm的陶瓷耐压结构在115 MPa压力下发生水下内爆，在距离球心6 cm处的冲击波压力约为环境初始压力的6.7倍；在距离球心26 cm处的冲击波压力约为初始压力的1.8倍。

4)耐压结构外部的冲击波压力峰值与到球心距离呈负指数幂函数关系，对115 MPa压力下半径为5 cm的耐压结构而言，其衰减系数为-1.343。

5)在万米级深海压力下，陶瓷耐压结构内爆后，其外部监测点的冲击波压力峰值与球体半径呈正比例关系。

将万米级深海陶瓷耐压结构简化为无厚度的球型气腔进行纯流体数值模拟，若发生内爆的结构是由金属等延展性较强的材料制成，则材料属性和壳体尺寸会对内爆产生一定的影响，未来可建立带壳体的耐压结构模型，对不同材质的耐压结构进行内爆的流固耦合数值模拟。此外，深海潜器中通常布置有多个耐压结构，考虑到耐压结构之间的相互影响，对深海耐压结构内爆的研究不能局限于单个耐压结构中，未来有待开展两个及多个深海耐压结构殉爆的研究。