膜态沸腾球体水下运动减阻特性
2019-03-13李佳川魏英杰王聪夏维学
李佳川, 魏英杰, 王聪, 夏维学
(哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001)
0 引言
减小液体中运动物体的阻力是流体动力学中的一个重要问题。较低的阻力意味着更快的速度和更少的能源消耗。减小阻力的方法有很多,例如应用聚合物添加剂[1]、超空泡[2-3]、微气泡注射[4-5]、疏水涂层[6-8]等。这些方法主要是通过改变物体的表面特性或通过改变物体附近流体的密度来实现减阻功能。
当物体的表面温度远高于液体沸点时,周围液体汽化后的蒸汽不断汇聚,形成连续的蒸汽膜,称为膜态沸腾过程。由于蒸汽膜的绝热性会使热量交换变得很差,物体壁面会达到很高的温度,甚至有烧毁的危险,在热工程领域中,一般要避免膜态沸腾的发生。最近的研究表明,利用膜态沸腾形成的蒸汽膜能够实现减阻功能[9-13],因此膜态沸腾减阻成为一种较新的减阻方法。
膜态沸腾产生的蒸汽膜具有滑移效应,类似于嵌入超疏水性壁面的空气垫。然而超疏水性壁面的减阻效果有限,且在水压及水流冲刷作用下空气层很快会消失。持续加热物体可以在壁面处形成连续稳定的蒸汽膜,减小摩擦阻力。Saranadhi等[9]研究表明,当雷诺数在26 100~52 000范围内时,摩擦阻力可以减小80%~90%,减阻效果非常明显。
膜态沸腾生成的蒸汽膜,不仅可以减小摩擦阻力,还可以减小压差阻力。Vakarelski等[10]采用一种沸点和汽化潜热均低于水的氟化液体,对膜态沸腾阶段球体在该液体中的自由下落过程进行了研究,结果表明蒸汽膜的存在可以降低球体受到的压差阻力,使总阻力减小85%. 随后,Vakarelski等[11-12]采用不同液体对膜态沸腾球体绕流过程进行了详细的实验研究,分析了液体温度、球体温度和雷诺数等对减阻特性的影响。
目前,对膜态沸腾球体绕流特性的研究还处于初步阶段,相关减阻机理还需要进一步研究。由于膜态沸腾球体绕流过程涉及相变、湍动、流动分离和多相流动等复杂物理问题,至今还没有学者对该过程进行数值仿真研究。Gruncell等[14]对超疏水性球体的绕流过程进行了数值仿真研究,通过固定一层厚度相等且不变形的空气层等效疏水特性。对于膜态沸腾球体绕流过程,不同表面位置蒸汽膜的厚度不同,且存在蒸汽堆积现象,因此用Gruncell等[14]的方法进行等效模拟的准确性较低。
本文采用Mixture多相流模型、剪切压力传输(SST)k-ω湍流模型,耦合蒸发- 冷凝相变模型,对膜态沸腾球体绕流过程进行数值仿真研究。研究膜态沸腾球体绕流特性,分析雷诺数对阻力特性的影响,并对减阻机理进行研究。
1 数值计算方法
1.1 控制方程
为了识别球体表面蒸汽膜,球体壁面附近需要较密的网格,使得整体网格量较大,因此本文将球体绕流问题简化为二维轴对称流动问题,总体网格量约为44万。
采用Mixture多相流模型描述各相流体体积分数。水和水蒸汽的混合密度为
ρm=ρl(1-αv)+ρvαv,
(1)
式中:ρl、ρv分别为水的密度和水蒸汽的密度;αv为水蒸汽的体积分数。
质量守恒方程为
(2)
式中:t为时间;ui(i= 1, 2)为平面笛卡尔坐标系下的速度分量。
动量守恒方程为
(3)
式中:uj(j=1, 2)为平面笛卡尔坐标系下的速度分量;p为压力;g为重力加速度;F为表面张力;τij为黏性剪切应力,
(4)
δij为Kronecker符号,μm为混合黏度;uk(k=1,2)为平面笛卡尔坐标系下的速度分量。
能量守恒方程为
(5)
式中:cp为定压比热;T为温度;k为导热系数;Φ为相变潜热产生的能量源项,
(6)
Lv为汽化潜热,fv=ρvαv/ρm为汽相质量分数。
水汽化成水蒸汽的相间传递过程采用蒸发- 冷凝模型进行模拟,其输运方程表达式为
(7)
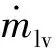
(8)
(9)
cflv与cfvl分别为蒸发和冷凝系数,Ts为水的饱和温度。
球体绕流问题,需要较精确地预测流动分离位置,因此本文湍流模型选用可以较好地模拟分离问题的SSTk-ω模型。
1.2 计算域及网格划分
计算域、边界条件和局部网格划分如图1所示。本文计算域采用二维轴对称模型,球体直径为D,计算域径向直径为10D,高度为15D. 球体壁面采用无滑移壁面边界条件,侧边壁采用滑移壁面边界条件,下边界为速度入口,上边界为压力出口。球体位置固定不变,重力方向向下,来流方向向上,入口速度u为定值,可以等效模拟球体在水中匀速自由下落的过程。本文网格采用C-Block划分策略,为了识别蒸汽膜,球体表面附近网格进行了加密,球体壁面附近第1层网格高度设置为1 μm,满足SSTk-ω湍流模型所要求的y+<1,壁面附近网格高度增长因子设置为1.05,C-Block外层网格高度增长因子设置为1.1.

图1 计算域及局部网格划分Fig.1 Computational domain and local mesh generation
1.3 数值方法验证
目前仅有少数学者针对膜态沸腾球体水下运动过程进行了实验研究,本文将数值仿真得到的膜态沸腾球体绕流运动阻力系数与Vakarelski等[11]的膜态沸腾球体水下自由下落实验得到的阻力系数进行对比,以验证本文数值方法的准确性。球体水中自由下落过程中,受到水的阻力与运动速度的平方呈正比,球体下落的初始阶段速度较小,球体做向下加速运动,当球体速度达到一定值时,水的阻力与球体重力相等,球体将做匀速运动。
球体水中运动的阻力系数为
Cd=2Fd/(πR2ρlu2),
(10)
式中:Fd为球体受到的阻力;R为球体半径;u为球体水中运动速度。
当球体匀速运动时阻力与重力相等时,阻力系数可以表达为
Cd=[8g(ρ-ρl)R]/(3ρlu2),
(11)
式中:ρ为球体密度。
根据Vakarelski等[11]得到的球体匀速运动速度,利用(11)式计算出球体的阻力系数。
如图1所示,本文数值仿真球体位置固定,水相对于球体向上运动,水流速度为u,重力方向向下,可以等效模拟Vakarelski等[11]的球体在水中匀速下落过程。表1为本文数值仿真与Vakarelski等[11]实验得到的膜态沸腾球体水中匀速运动阻力系数对比,表中雷诺数Re=ρluD/μl,μl为水的黏度。
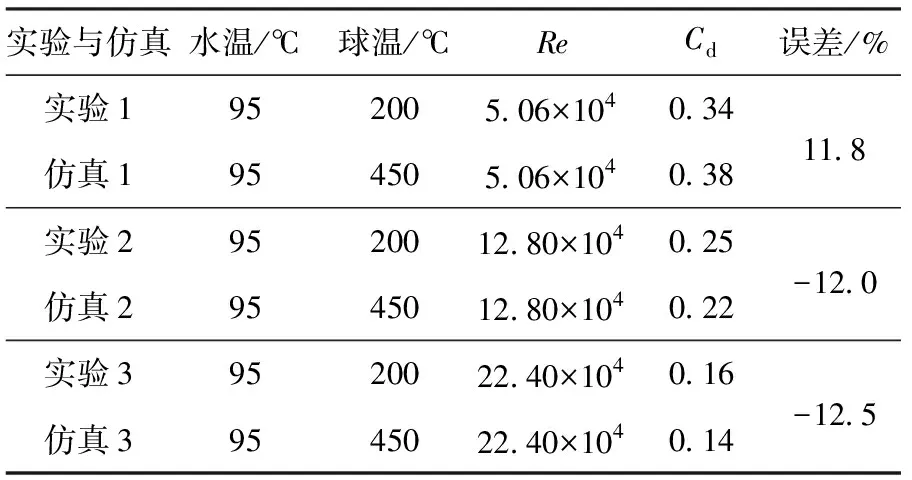
表1 数值与实验阻力系数对比
从表1中可以看到,本文数值仿真选用的球体温度与Vakarelski等[11]实验选用的球体温度不同。Vakarelski等[11]采用超疏水性球体,相对于亲水性球体,超疏水性球体可以在较低温度下形成膜态沸腾[11,15]。由于同时考虑流动、传热、相变和表面润湿性比较复杂,不易于模拟,本文数值仿真没有考虑球体表面润湿性,为了形成膜态沸腾,球体温度设置为450 ℃的较高温度。Vakarelski等[10-12]的研究表明,球体发生膜态沸腾后会继续升高球体温度,球体达到匀速时的速度u变化较小,可以忽略,由(11)式可知,膜态沸腾球体的阻力系数随球体温度变化较小,可以忽略。因此,可以采用表1所示的不同球体温度与Vakarelski等[11]的实验结果进行对比。在Vakarelski等[11]的研究中,球体水中下落时间小于1.5 s,且由于蒸汽具有较低的导热系数,球体温度降低较小。由于沸腾球体绕流物理过程复杂,本文数值仿真进行了简化,仅对定常状态下的膜态沸腾球体绕流进行研究,球体温度恒为450 ℃.
从表1中可以看到,3种不同Re下的数值仿真Cd值与Vakarelski等[11]实验的Cd值最大相差-12.5%. 由于本文数值计算简化为二维轴对称问题,忽略了尾流不对称性对阻力的影响,会与实际流动过程略有偏差。但阻力系数范围与实验范围一致,并随Re的增加而大幅度减小。因此可以采用本文数值仿真方法对膜态沸腾球体在水中的运动过程进行研究,并分析相应的减阻机理。
2 计算结果及分析
2.1 膜态沸腾球体绕流特性
本文对比分析Re=1.28×105条件下膜态沸腾球体与普通球体的绕流特性。其中水温均为95 ℃,膜态沸腾球体球温为450 ℃,普通球体球温为95 ℃. 两种球体的球体直径D为20 mm,水流速度u=2 m/s. 计算所得的普通球体阻力系数为0.48,计算所得的膜态沸腾球体阻力系数为0.22(见表1)。
当普通球体流动处于亚临界Re范围内,即5×103≤Re≤3×105时,阻力系数约为常数,Cd≈0.44. 本文计算所得的普通球体阻力系数在0.44附近,相差约为9.1%. 膜态沸腾球体的阻力系数约为普通球体的50%,由此可知膜态沸腾可以大幅度减小球体受到的阻力。
为了便于分析,对球体表面位置进行规定,如图2所示,水流方向向上,球面底端位置P对应角度θ=0°,球面中端位置M对应θ=90°,球面顶端位置N对应θ=180°.
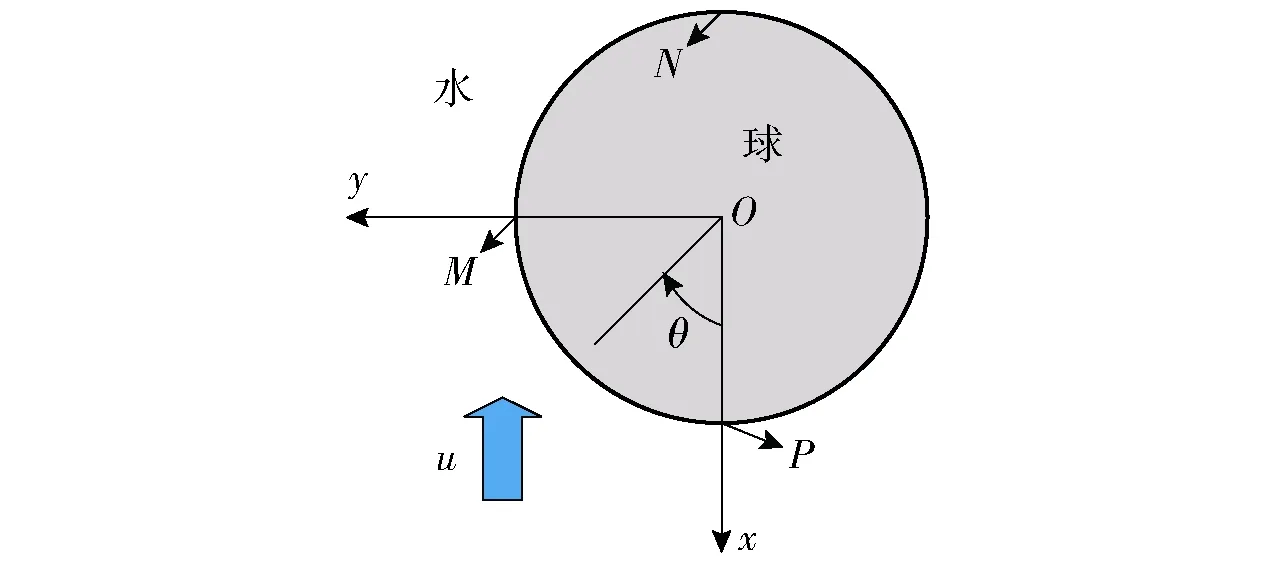
图2 球体表面位置示意Fig.2 Schematic diagram of surface position of sphere
图3(a)所示为膜态沸腾球体绕流的水蒸汽云图,图3(b)所示为球体周围温度云图。当球体表面温度远高于水的沸点时,汽化成的水蒸汽汇聚到一起,使球体被一层水蒸汽膜包裹,如图3(a)中M点处的水蒸汽云图放大部分所示。球体尾部由于旋涡与回流的影响,沿流动方向生成汽泡云。由于球体周围温度大部分较低,且温度范围为95~450 ℃,跨度较大,图3(b)仅显示95~130 ℃部分的温度云图,其中温度大于130 ℃部分显示的颜色与130 ℃温度一致。由于水蒸汽的导热系数远小于水,蒸汽膜的存在使高温球体与周围水隔开,降低了球体的传热能力,温度场中大于130 ℃分布在球体表面附近的蒸汽膜内,球体尾部的汽泡云温度在130 ℃以下。
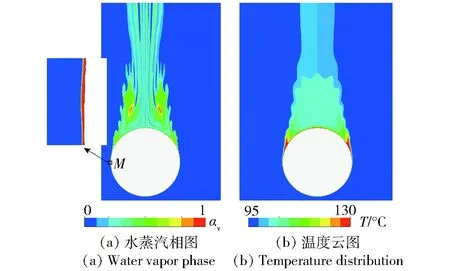
图3 膜态沸腾球体绕流水蒸汽与温度云图Fig.3 Water vapor phase and temperature distribution
图4所示为普通球体与膜态沸腾球体的绕流速度v矢量图。由图4可见:球体侧面位置附近流速较高,尾部旋涡区速度较低;由于蒸汽膜的润滑作用,膜态沸腾球体绕流速度最大值要大于普通球体;膜态沸腾球体尾部低速区比普通球体窄。

图4 普通球体与膜态沸腾球体绕流速度矢量图Fig.4 Velocity fields of ordinary sphere and film boiling sphere
图5所示为普通球体与膜态沸腾球体的绕流流线图。由图5可见,球体在水中受到的阻力分为摩擦阻力与压差阻力,摩擦阻力由水的粘滞性引起,压差阻力由球体上表面和下表面的压力差产生。对于普通球体,当5×103≤Re≤3×105时,摩擦阻力占总阻力的比例较小,球体主要受压差阻力的作用。针对球体绕流问题,压差阻力主要由球体表面发生流动分离的位置决定,流动分离发生的越迟缓、越靠近球体尾部,球体绕流受到的压差阻力就越小。对于普通球体,球体表面流动分离发生在M点稍前的位置,即分离角度略小于90°[16],与图5(a)所示的结果相吻合。

图5 普通球体与膜态沸腾球体绕流流线图Fig.5 Streamline distributions of flows around ordinary sphere and film boiling sphere
Vakarelski等[10]对膜态沸腾球体在氟化液体中的自由下落过程进行了研究,发现膜态沸腾球体达到匀速时的速度要大于普通球体。结果表明,膜态沸腾阶段产生的蒸汽膜使流动分离位置向尾部移动,减小了球体受到的压差阻力,从而减小了球体受到的总阻力。与Vakarelski等[10]的研究相吻合,图5(b)所示膜态沸腾球体绕流,分离位置位于球体表面的尾部区域。相比于普通球体,膜态沸腾球体尾部旋涡区较窄,尾部形状趋于流线型。流线形状与图3所示水蒸汽相与温度相云图尾部形状一致。本文的数值方法可以较好地模拟膜态沸腾球体绕流问题。
2.2 不同Re膜态沸腾球体绕流特性
对于普通球体,阻力系数大小主要与Re有关。当Re很小(Re<1)时,黏性力起主要作用,阻力系数可以表达为Cd=24/Re. 随着Re增大,Cd不存在解析解,Cd随着Re增大而减小。当5×103≤Re≤3×105时,流动分离点几乎不发生改变,Cd几乎与Re无关。当Re达到临界值,即Re≈3.5×105时,边界层转化为湍流边界层,使流动分离位置向后移动,阻力系数减小为Cd≈0.1. 不同于普通球体,Vakarelski等[10-12]的实验表明,在亚临界流动范围内,即5×103≤Re≤3×105时,膜态沸腾球体阻力系数随Re增大而减小。
本文采用数值仿真方法研究亚临界流动范围内Re对膜态沸腾球体阻力系数Cd的影响。Re分别取值5.06×104、1.28×105和2.24×105. 如表1所示,得到的阻力系数分别为0.38、0.22和0.14,与Vakarelski等[11]的实验结果相吻合。这一结果表明,随着Re增大,膜态沸腾球体绕流运动的阻力系数逐渐减小。在2.1节已经对比分析了Re为1.28×105时普通球体与膜态沸腾球体的绕流特性,该节主要分析Re分别取值5.06×104和2.24×105时的膜态沸腾球体绕流特性,其中球体直径均为20 mm,水流速度分别为0.79 m/s和3.50 m/s.
图6~图8所示分别为两种Re条件下膜态沸腾球体绕流的水蒸汽相图、速度矢量图和流线图。由图6~图8可以看出,Re越大,球体尾部水蒸汽云越趋于流线型,尾部低速旋涡区越窄,流动分离位置越靠近球体尾部。
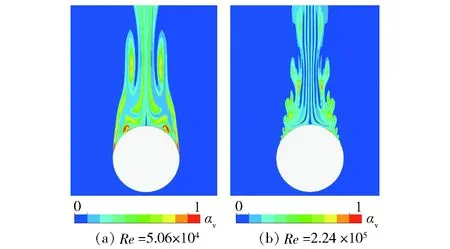
图6 不同Re膜态沸腾球体绕流水蒸汽相图Fig.6 Water vapor phase distributions of flows around film boiling spheres with different Re

图7 不同Re膜态沸腾球体绕流速度矢量图Fig.7 Velocity fields of flows around film boiling spheres with different Re
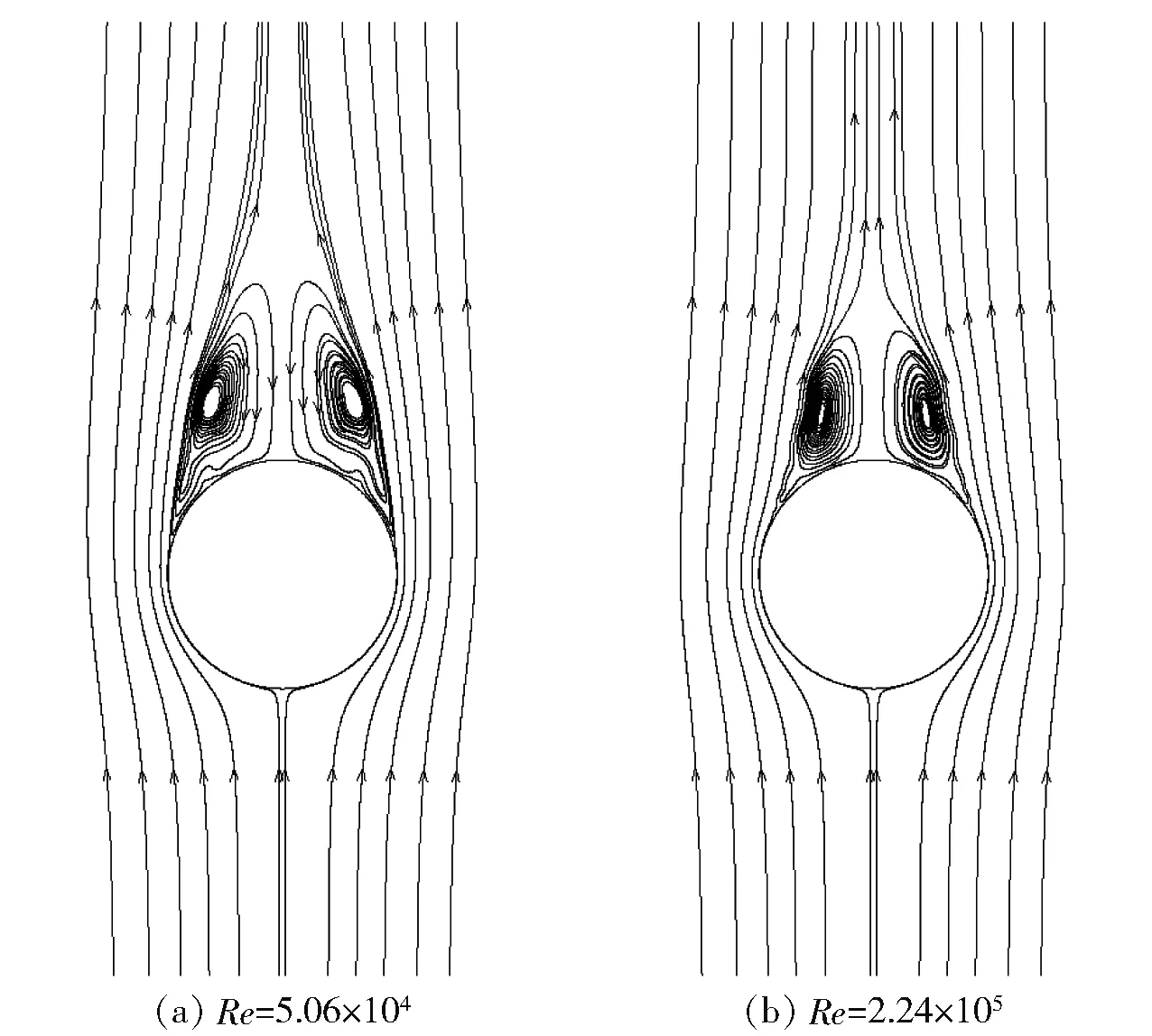
图8 不同Re膜态沸腾球体绕流流线图Fig.8 Streamline distributions of flows around film boiling spheres with different Re
为了清晰对比不同雷诺数膜态沸腾球体绕流的流动分离特性,图9给出了不同雷诺数膜态沸腾球体及常温球体绕流近壁面流线对比图。由于在亚临界流动范围内,常温球体绕流的流动分离位置几乎保持一致,图9仅呈现Re=1.28×105的普通球体近壁面流线。分析图9可知,普通球体绕流的流动分离位置为θ≈85°,略大于Achenbach[16]实验所得的θ≈82.5°.Re取值分别为5.06×104、1.28×105和2.24×105时膜态沸腾球体绕流的流动分离位置分别为θ≈99°、θ≈108°和θ≈120°.膜态沸腾球体绕流与普通球体相比,流动分离位置偏向尾部,且随着Re增大,分离角度逐渐增大。在亚临界流动范围内,阻力大小主要由压差阻力决定,即由流动分离位置决定。因此,膜态沸腾绕流受到的阻力要小于普通球体,且随着Re增大,减阻效果越明显。

图9 近壁面流线对比Fig.9 Comparison of streamlines near the sphere surface
2.3 膜态沸腾球体绕流运动减阻机理
流动分离的条件为逆压梯度,流动分离发生的根本原因为流体黏性的存在。在分离区附近,流体的动能不仅逐渐转变为压强能,同时边界层内的粘性流体(特别在临近壁面处)受到壁面的滞止作用(表现为切应力),不断消耗动能。当靠近壁面处流体的动能全部耗尽,流体微团将在分离点处停滞不前,并发生堆积。分离点后在反向压差作用下,壁面附近产生回流,排挤上游流体使流动在分离点处发生分离。Vakarelski等[10-11]的实验研究指出,膜态沸腾球体被一层蒸汽膜包裹,减小了切应力对流体的滞止作用,使流动分离点向后移动。
图10所示为Re=1.28×105时普通球体与膜态沸腾球体绕流在图2所示M点附近的速度矢量对比图。由图10可见,普通球体壁面附近速度梯度较小,距离壁面较远位置速度才达到外部主流速度。由于水的黏度远大于水蒸汽,膜态沸腾球体在蒸汽膜内,速度梯度较大,在距离壁面较近的蒸汽膜外部具有较大的流动速度。且膜态沸腾球体外层速度与来流速度平行,普通球体速度稍偏离来流方向偏向远离球面的方向。图11给出了M点处沿y轴方向流体的x轴方向无量纲速度v(v=vx/u,vx为x轴方向的流动速度)对比,其中来流方向为x轴负方向。球体直径为20 mm,M点处y轴坐标值为10 mm(位置与方向规定见图2)。由图11可知:普通球体M点位于流动分离点之后近壁面位置发生回流,因此普通球体近壁面处x轴方向速度为正值(与来流方向相反);蒸汽膜的存在,使膜态沸腾球体沿y轴方向流体速度增长较快,且达到的速度最大值略大于普通球体。
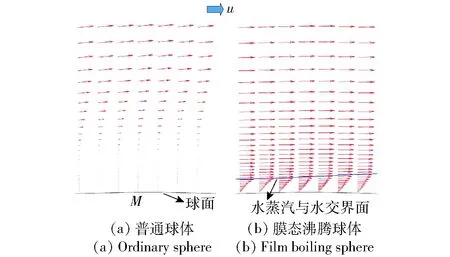
图10 普通球体与膜态沸腾球体在M点附近速度矢量Fig.10 Velocity vectors of ordinary sphere and film boiling sphere near point M
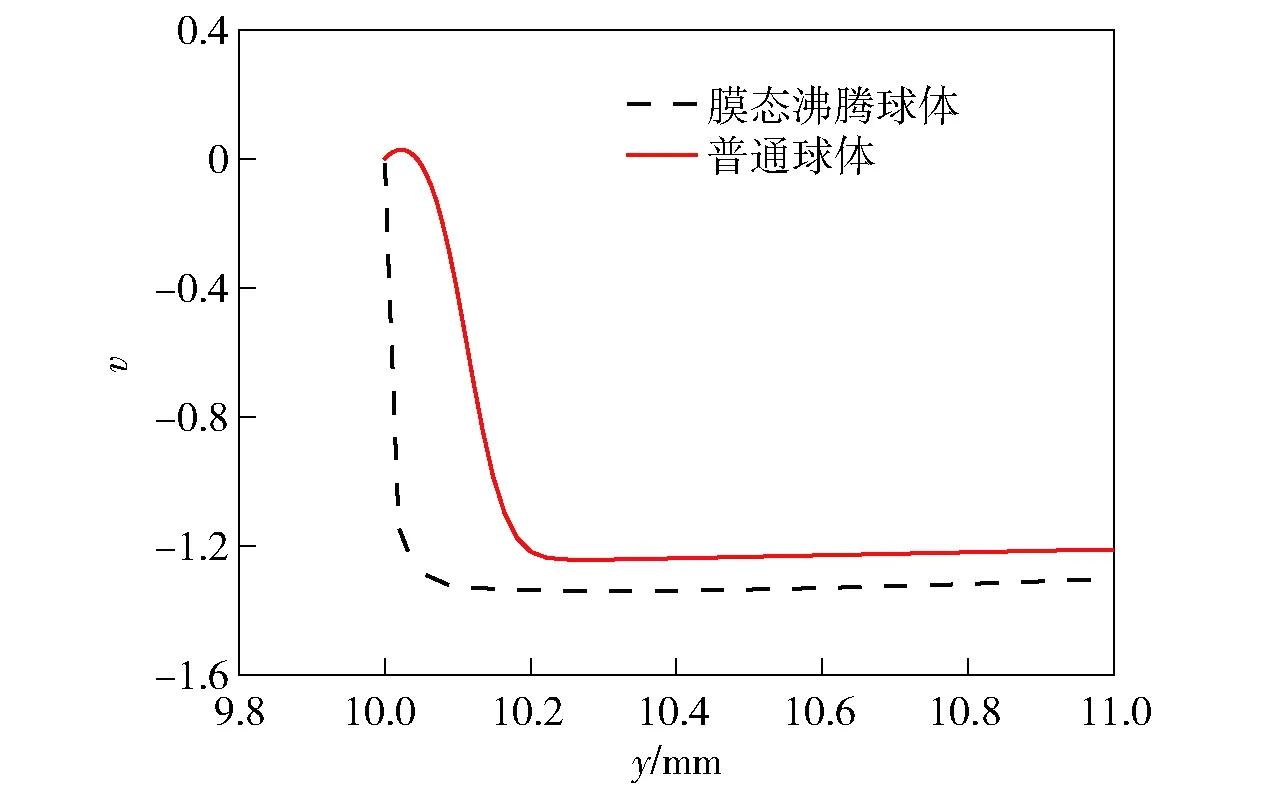
图11 M点处沿y轴方向流体的x轴方向无量纲速度对比Fig.11 Comparison of fluid velocities in the direction of x at point M
将蒸汽膜与球体看作整体,膜态沸腾球体的绕流运动可以等效为流体绕蒸汽膜的运动,则壁面处的无滑移边界条件可以转换为蒸汽膜处的滑移边界条件。蒸汽膜边界处黏滞力的减小使膜态沸腾球体绕流流动分离点向球体尾部移动,减小了球体受到的阻力。
由2.2节可知,Re对膜态沸腾球体绕流的阻力特性有较大影响。Gruncell等[14]通过在球体表面固定一层厚度相等且不变形的气体层,对超疏水球体的绕流过程进行了数值仿真研究,结果表明气体层的滑移效应使流动分离点向球体尾部移动,极大地减小了球体绕流受到的阻力。对于膜态沸腾球体的绕流过程,球体表面的蒸汽膜厚度并不处处相等。图12所示为不同Re膜态沸腾球体绕流蒸汽相体积分数为0.5的等值线图。由图12可知:蒸汽会在逆压梯度作用下发生堆积,使蒸汽膜外部流动发生分离;类似于普通球体,随着Re增大,堆积位置会向球体尾部移动;蒸汽膜的减阻作用,会由于蒸汽的堆积而受到抑制。因此膜态沸腾球体绕流过程中球体的阻力系数随着Re增大而减小。
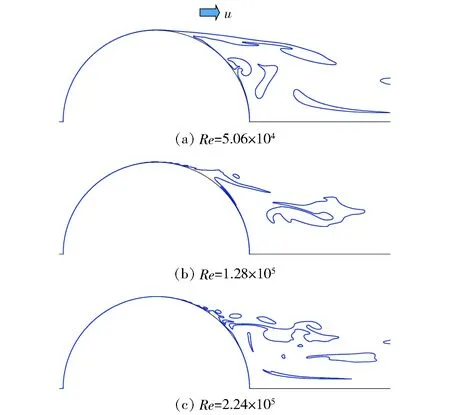
图12 不同Re水蒸汽相体积分数为0.5的等值线图Fig.12 Contour plot of 0.5 vapor fraction for different Re
3 结论
本文采用数值仿真方法对亚临界流动范围内膜态沸腾球体的绕流特性进行了研究,分析了Re对阻力特性的影响,并对膜态沸腾减阻机理进行了研究。主要得到以下结论:
1)本文数值仿真方法可以较好地模拟膜态沸腾球体绕流特性,得到的阻力系数与已有文献[11]的一致性较好。
2)由于水蒸汽的黏度远小于水,壁面附近蒸汽膜内部的速度梯度较大,相比于普通球体,膜态沸腾球体绕流在距离壁面较近的水蒸汽膜外部具有较大的流动速度,水蒸汽膜的滑移效应减小了壁面对流体的粘滞力作用,使流动分离点向尾部移动,使球体受到的阻力减小。
3)由于逆压梯度的存在,膜态沸腾球体生成的水蒸汽会在球体壁面尾部区域堆积,随着Re增大,堆积位置向后移动,延缓流动分离,阻力系数逐渐减小。
