乙醇偶合制备C4烯烃的数学模型

柯佳慧 蔡 琼 田丽歆 周文黎

（江汉大学 湖北·武汉 430056）

1 问题的提出

随着化工医药业的发展，烯烃原料具有清洁，可再生等特点，被广泛应用于生产生活中。而C4烯烃作为塑料，香精等主要原材料之一，其制备研究就显得更有意义。目前最常见的C4烯烃制备方法就是利用乙醇催化偶合，但过程中除了要考虑反应物的利用率以及生成物的量之外，还要考虑实际实验操作难度，以及反应生成的一些副产物也最好尽可能的小，那么就需要找到最佳的催化剂组合和温度，确保实验在相对安全便捷的情况下，生成尽可能多的有用生成物，以及使烯烃收率最优。

2 问题的分析

现已知某化工实验室针对两种催化剂装料方式1和2，其中分别在不同催化剂组合以及不同温度下做了一系列试验，得到生成物结果记录。数据显示催化剂是由Co负载量、Co/SiO2和HAP装料比以及乙醇滴加速度组合而来，实验温度大多为250℃～400℃，生成物也有相关记载，反应性能评价由乙醇转化率与C4烯烃选择性组成，此二者均为正指标。

首先，将数据集中的催化剂组合进行拆分，并对数据无量纲化，标准化处理。其次，利用Pearson相关系数分析不同特征之间的相关性强弱，得出不同特征对试验结果的大致影响。将拆分后的各数据集，分别按温度，Co负载量等等特征分组，将分组后的数据分别用TOPSIS模型计算，得到大概的各个特征对催化剂效果的影响趋势。最后，利用支持向量机模型对原有的拆分后的数据集进行训练与测试，用枚举法对这些特征的取值进行重组，得到关于装料方式，催化剂组合，温度的36036个组合，将得到的这些数据集放入前面训练过的SVM程序中运行计算，便可得出最大的生成物百分数，以得到对应最优的催化剂组合与温度。

3 模型的建立与求解

3.1 数据预处理

（1）拆分数据集：首先将催化剂按照Co负载量，Co/SiO2和HAP装料之比，乙醇加入的速度这三个特征值进行数据的拆分。但由于数据中含有Co/SiO2和HAP装料比相同但各自的值不同这一因素，为了消除这种比值相同但质量不同的影响，在此还增加了一个HAP的质量作为一个特征值，以便随意组合后可以得到每一个重要的影响因素的具体数值。其次数据集中有一些数据没有直观的数值，因此，我们针对每一种拆分数据进行了数值替代，具体替代方法如下：①feature1：Co负载量的数值替代。如Co/SiO2质量之比为1wt%=1:100，近似认为Co的负载量为1；②feature2：Co/SiO2和HAP装料之比的数值替代。通过查询资料得知装料比只有1:2，1:1，2:1三种情况，因此用0.5,1,2来代替。如Co/Si02装料为200mg，HAP装料为200mg，用1代替；③feature3：加入HAP的数值替代。例如数据显示HAP为200mg，则用200代替；④feature4：乙醇加入速度的数值替代。比如乙醇浓度为1.68ml/min，用1.68代替。

（2）标准化处理：根据题目需要，我们仅对生成物中乙醇转化率和烯烃选择性这两个因素作为实验好与不好的参考依据，此时该数据的显示方式为百分比，此类数据量级等均与其他数值类型不同，所以此时若直接代入原始数据，由于量级问题可能会对后续的结果造成影响，例如数值较大的数据对结果影响会较为突出，而数值小的数据对结果的影响可能会被“忽略不计”等问题。所以为了减小运算结果误差，我们针对上述问题对进行了标准化处理。由于我们的数据中，两个重要需求因素（乙醇转化率和烯烃选择性）都是正指标，所以我们是直接对其进行了离差标准化处理，使之范围均控制在区间[0,1]中。

3.2 相关性分析

Pearson相关系数的基本思想为任取两个变量X=[x1,x2,…,xn]，Y=[y1,y2,…,yn]，当变量为连续性数值且总体呈正态分布或接近正态分布时，通过计算x,y的离差平方和及离差平方和之积，求得相关系数r,从而确定其相关性强度。本文利用Python建立了相关系数矩阵，发现了不同催化剂组合，温度与乙醇转化率，C4烯烃选择性都是强相关的，相关系数达到了0.9左右，因此不需要筛选特征。

3.3 TOPSIS模型分析

针对标准化之后的数据，首先按温度由小到大排序，将温度相同的看作同一组，找到每一组最优值和最劣值，然后计算标准化之后的数据到这两个值的欧氏距离，然后得到距离的综合指标。发现温度对两个生成物的影响都是温度越高越好。同上处理方式，我们对装料方式等等，也进行了相应的处理，得到催化剂的装料方式1明显优于装料方式2，因此后续对于寻找最优实验组合时，可以不用考虑第二种装料方式。另外发现：Co负载量越小，得到的所需物相对越高；Co/SiO2和HAP装料之比1:1时对于乙醇的转化率效果较好；当HAP的质量越多时，转化率与选择性越高；加入乙醇的速度越慢则实验结果越好。

3.4 构建支持向量机回归模型

支持向量机方法是建立在统计学习理论的基础上，对特定训练样本的学习精度，Accuracy和学习能力。通俗来说，支持向量机就是通过给定的数据集中，找到一个超平面，使它能够尽可能的分开两类数据点，使这两类数据点距离该平面的距离最远，SVM就是要寻找这个最好的超平面，划分数据集。

依据前面针对催化剂组合特征对实验结果影响的研究结果，我们对原始数据中所给的5个指标进行了扩充，分别为：

①feature1:[0.3 0.4 0.5 0.7 0.8 1 1.5 1.9 2 2.5 4 4.5 5]

②feature2:[0.5 1 2]

③feature3:[10 25 33 50 67 75 90 100 140 170 200]

④feature4:[0.3 0.9 1.3 1.68 2.1 2.4]

⑤实验温度:[250 275 300 325 350 375 400]

利用Python对5组数据做笛卡尔积，将数据放入了不同的列表中，分别定义对两组数据，求笛卡尔积的封装函数two（）以及n组数据（n个列表）求笛卡尔积的封装函数process（），其中n组数据求笛卡尔积函数采用递归方法，将所得笛卡尔积用for循环与split（）方法以单元格为单位进行数据切分，最终共有36036个测试数据组合。

通过前面已经测试检验过的支持向量机回归模型遍历所有的36036个组合，用温度划分之后进行最优排序，得到最终结果为：

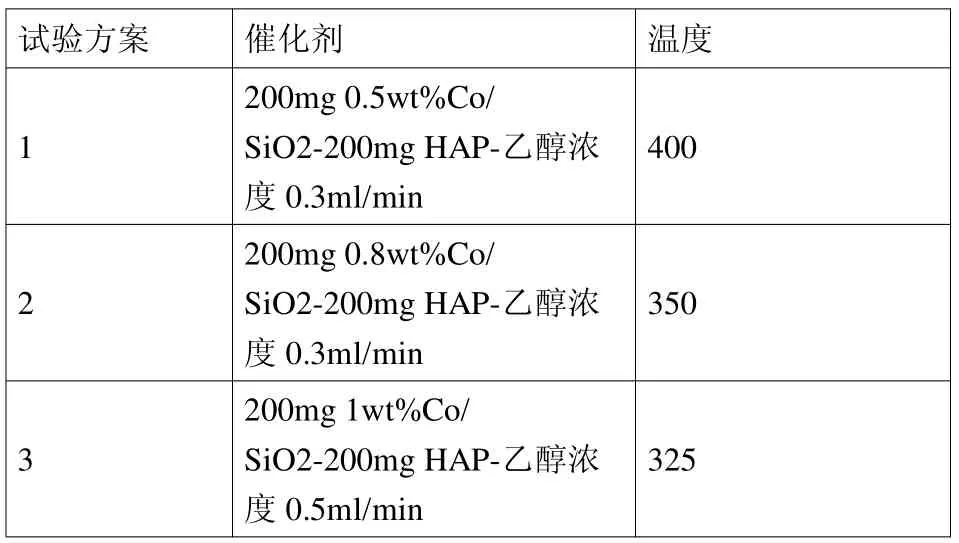
试验方案 催化剂 温度1 200mg 0.5wt%Co/SiO2-200mg HAP-乙醇浓度0.3ml/min 400 2 200mg 0.8wt%Co/SiO2-200mg HAP-乙醇浓度0.3ml/min 350 3 200mg 1wt%Co/SiO2-200mg HAP-乙醇浓度0.5ml/min 325

出于对试验安全性，节约成本等考虑，我们选择试验方案2。

4 模型的评估与改进

4.1 模型的优点

（1）SVM模型比直接线性回归要拟合度更高，实用性较强，可以应用于许多非线性的实际问题。

（2）本文中创建了封装函数，即代入任何类似数据都可以直接得到计算结果，用很少的实验次数，得到最好的实验结果，对于实验评估与实现都有很大的意义，具有很好的推广性。

4.2 模型的缺点

由于试验数据过少，导致我们模型的稳定性不高；对于化学反应过程中的其他副产品没做过多研究，实际操作中会面临许多的不可控因素；支持向量机（SVM）的测试机中拟合度r2还不够高，还有改进空间。

4.3 模型的改进

后面可以通过询问化学老师等，了解一下其他副产物对实验是否有影响，那样就会有更多的影响因子，对我们的程序测试也更加有利。针对支持向量机SVM的情况，我们可以对数据集的结果进行分类处理，放在分类器中，得到不同的分类组合，使结果拟合到这些组合中，以便精度更高，效果更加明显。