“六步法”在小学数学概念教学中的应用研究——以“因数与倍数”为例

禹 迪，田应仟

(黔南民族师范学院教育科学学院，贵州都匀，558000)

一、引言

《义务教育数学课程标准(2011年版)》指出：“教师要发挥主导作用，处理好讲授与自主学习的关系，引导学生独立思考、主动探索、合作交流，使学生理解和掌握基本的数学知识与技能，体会和运用数学思想与方法，获得基本的数学活动经验。”[1]数学概念在小学数学中是重要的基础内容，是学生形成数学思维的基础。掌握基本的数学概念，不仅可以在一定程度上使学生打好数学基础，还可以培养他们的数学素养。

然而，在当前的小学数学概念教学中，部分教师采取的教学方法较为单一，忽视对概念形成过程的讲解，且缺乏对学生语言阅读能力和表达能力的培养，影响了学生对数学概念的学习效果。以忽视对概念形成过程的讲解为例，学习数学概念的过程应是先感知，由感知表象到理解抽象，最后由抽象回到具体的过程，但目前的数学概念教学多采用“师问生答”的传统教学方法，未能让学生充分参与课堂教学，学生往往处于被动接受的状态；同时，部分教师习惯让学生死记硬背数学概念，再通过题海战术来巩固概念，不重视概念形成过程的讲授。在这种情况下，有时学生还未充分感知、体验概念的含义，教师就已经结束概念的讲解，导致学生对概念的理解仅仅停留在表面，不能灵活运用概念及相关知识来解决实际问题，更不利于数学核心素养的形成。

有学者以“数学活动促进数学核心素养发展”理念为指导，提出了“读、说、讲、练、问”五环综合数学活动。[2]周淑红参照这五个基本活动环节，提出小学生数学“RQSES”(Reading阅读、Question提问、Study探究、Expression表达、Summary总结)五步训练法。[3]

学生在学习新概念时，有一个从具体到抽象，再从抽象到具体的过程。练习在这个过程中扮演着重要的角色，其目的是让学生熟练掌握数学概念的内涵，巩固概念，进一步加强数学概念和生活的联系。因此，本文在“五步训练法”的基础上加了练习(Exercise)，由此而形成小学数学概念教学“六步法”(RQSEES)的内涵，即阅读、提问、探究、表达、练习及总结。下文以人教版五年级数学下册“因数与倍数”为例，探讨“六步法”在小学数学概念教学中的应用。

二、“六步法”在小学数学概念教学中的应用

(一)阅读

阅读是数学学习活动之一，是学生自主获得知识的一种方式。阅读是动眼、动口、动手及动脑的有机结合、协调统一的过程。数学阅读不仅仅局限于数学课本的内容，同时需要多方面搜集对数学有用的信息。会阅读的学生会思考以下问题：所阅读的数学材料是关于什么的内容？这个数学结论从何而来？其作用是什么？阅读时边读边思考，可以提高学生的注意力，也是培养学生思维的首要环节。教师首先要指导学生读出对概念的初步印象和概念的关键地方，其次读出心中的疑惑，最后读出概念真知。

阅读教材时要做到“读”“思”“查”三者结合。以“因数与倍数”这一概念的教学为例，在阅读教材时，教师要给学生一些明确的要求，如“一读”“二思”“三查”。一读，是认真读教材内容两遍以上，在认为重要的地方画线并做适当的批注。二思是思考“‘因数与倍数’研究的是哪些数？为什么是这些数？”“因数与倍数的概念是什么？它们之间有什么关系？”“通过阅读，还有哪些疑惑？”。三查是学生可以根据自己的实际情况查阅相关资料，以巩固自己的阅读成果。

这样的安排让学生的阅读有了具体的抓手，避免了阅读的盲目性和无序性。久而久之，学生可以养成数学阅读的好习惯，也会从数学阅读中获得新发现。阅读的过程就是锻炼思维的过程，学生通过数学阅读能够对概念进行初步感知，能够更准确地了解数学概念的相关信息，逐渐掌握一定的数学阅读方法，增强阅读自学能力。

(二)提问

提出一个问题往往比解决一个问题重要。学生提出问题，才会积极认真地思考。学生的问题意识越强烈，思维越活跃，进步也就越快。因此，教师设置相应的问题情境就显得尤为关键。问题情境应该贯穿于整个课堂之中。学生问题意识的培养依赖教师的教学设计，教师要了解学生的实际情况，找准学生的最近发展区，用多种方式呈现问题情境，激发学生的问题意识，使学生有问题可问。教师应该根据数学学习内容的不同创设不同的问题情境，激发学生的问题意识，让学生享受提出问题及解决问题的过程。

以“因数与倍数”的教学为例，教师可以首先出示“漂亮”一词，该词有两层含义：一是好看美观，二是出色。同一词语有着不同的意思，而本课研究的“因数与倍数”和学生之前了解的“因数与倍数”有区别也有联系。例如：1.2×3=3.6，其中各部分的对应名称为“因数×因数=积”，学生之前了解的因数有的是整数，有的是小数。在这个等式里，能说3.6是3的1.2倍，3.6是1.2的3倍。从这一例子中，学生可以理解以下知识：“倍”可以表示两个数的商，是一种数量关系，而商可以是整数、分数、小数等多种表现形式。

接下来，教师可以出示一系列除法算式，并提出以下问题：“如果要对这些算式进行研究，那得怎么研究？”这一问题可以把课堂交给学生。通过课前阅读，学生一般可以提出“把这些算式分类”的建议。分好类后，学生往往会产生新的疑问：“为什么要分类？难道是因数与倍数只需要整数而且被除数除以除数要除尽吗？为什么不要有小数和除法中有余数的？因数与倍数之间有什么关系？这里的倍数与之前学过的倍有什么不同？”这些问题的最终目标是弄清楚什么是因数、什么是倍数。虽然学生经过课前阅读对这些问题有了初步的认识，但往往还处在表面层次，需要进一步探索。学生的提问促进了其思维的发展，一些学生通过提问“开窍”，对学习更加积极和自信。

(三)探究

概念教学不是把概念硬塞给学生，让学生死记硬背，也不是咬文嚼字地讲授概念，而是根据学生已经有的经验引导和鼓励学生主动探索，让学生了解概念的形成过程。因此，探究活动在数学概念教学中不可或缺。学生能在探究中感知概念、形成概念、完善认知结构，并在操作过程感受数学的思想和方法。另外，教学情境可以产生数学问题，而教学探究来源于数学问题，因此，教师要把情境、问题和探究紧密结合起来。

1.4 统计学方法 采用SPSS 22.0统计软件对数据进行分析。计数资料以百分比表示，采用χ2检验；计量资料以x±s表示，采用t检验。以P<0.05为差异有统计学意义。

在“因数与倍数”的探究活动中，教师可以借助拼接长方形的数学活动，使学生在构建因数与倍数的概念时获得经验支撑，加深对概念的理解。[4]在探究的过程中，学生能体会因数与倍数的概念以及为什么因数与倍数是自然数(一般不包括0)。教师应把数学概念形成的过程变为在问题情境中操作、思考的过程，让学生通过探究体验概念的本质属性，逐渐形成正确丰富的概念表象，并逐渐把握概念的内涵，在大脑中形成概念。教师还要重视学生思维的发散，选择的探究内容应在学生的最近发展区内，既有挑战性又有可达成性。

数学概念教学中的探究活动旨在让学生通过探究建立正确的概念表象，逐渐把握概念的内涵，最终在大脑中进行自动化建构，抽象出概念特有的性质，从而对数学概念的认识由感性上升到理性阶段。

(四)表达

第斯多惠的发展性教学观认为，一切教学的最高目的是发展学生的思维和语言表达能力，以及借助理性的领会和研究新教材、新问题的能力，而绝不是简单地传授科学知识。[5]学生在讨论概念形成的过程中，会用数学语言解释、阐述或证明自己的研究结果，这也是对数学思维的梳理。数学表达是学生将数学概念内化为认知结构的表现。教师要抓住数学重要知识，分析教材，组合教材，运用符号、文字等多元化表达，不断优化概念的呈现方式。在注重数学表达的课堂上，学生不仅要看懂概念，还要讲出概念，即能够用自己的语言表达对概念的理解。

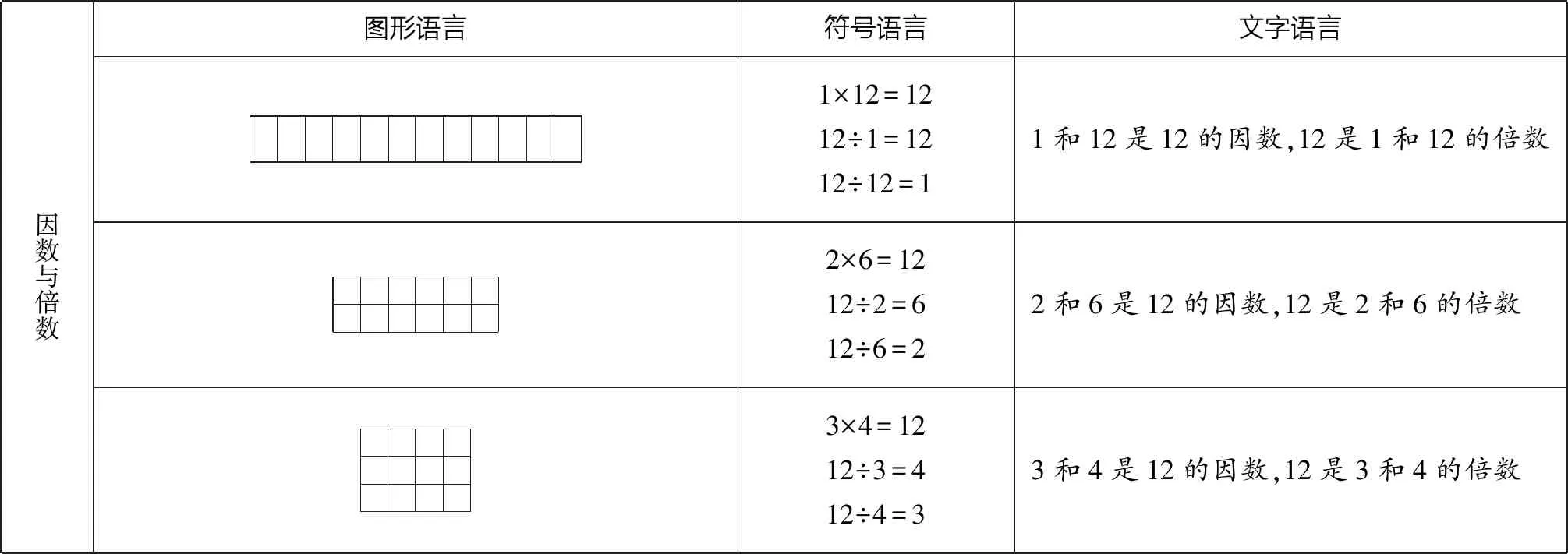
表1 “因数与倍数”概念的多元化表达

表1展示了“因数与倍数”概念的多元化表达，同时从多角度揭示了概念的内涵。对于同一概念来说，其定义可以选择不同的定义性特征。教师在教学中要引导学生多层面地感知概念，学生一旦建立了概念域，就会加深对该概念的理解。例如，“因数与倍数”的概念可以有以下几种表达方式：(1)在整数除法中，如果商是整数而没有余数，我们就说被除数是除数的倍数，除数是被除数的因数；(2)一个整数能被另一个整数整除，这个数就是另一个数的倍数，另一个数就是这个数的因数；(3)如果A×B=C(A、B、C都是0以外的自然数)，那么A、B都是C的因数，C是A、B的倍数。

在这样的概念表达中，学生可以学会用数学语言解释、阐述或证明自己的研究结果，这是对数学思维的梳理，也是将数学概念内化为认知结构的表现。对平时课堂上不爱表达的学生，教师也应多给予他们机会，让他们充分展现所学成果，以加深对所学概念的认识。

(五)练习

一是练习有层次。教师在设计练习题时，由于学生对知识的掌握情况不同，教师不能用一个标准去衡量所有的学生。在练习环节，教师需要尊重学生的主体性，在对作业的难易度和数量进行合理分层后，让学生自主选择习题进行分析和解答，这样既能体现作业分层实施的理念，又能培养学生自主学习的能力。

二是练习有趣味。单纯做练习，难免会比较枯燥，因此，教师可以将练习设计得丰富有趣。例如，教师可以充分发挥学生的主动性，让学生分组竞赛，互相出题、互相批改，而这也是数学概念由抽象回到具体的过程。

三是练习生活化。生活是数学知识的来源，对数学的学习最后也要回归生活。教师在进行概念练习设计时也应把握这一理念，确保数学概念练习生活化，以推动学生更好地理解并运用概念。例如，在“因数与倍数”的概念练习中，教师可先为学生呈现以下材料：

古时候，人们把数字分为阳数和阴数，奇数是阳，偶数是阴。阳数中九最高，五居正中，所以“九”和“五”象征着帝王的权威，称为“九五之尊”，代表至高无上的权威。皇帝喜欢把“九”这个数字用在建筑上，北京故宫的角楼相传有九梁、十八柱、七十二脊。

之后，教师可以让学生在上面的文字中找到与9有关的数，并说说它和9的关系。教师也可以引导学生找到自己学号的因数和倍数。这样的设计既开阔了学生的视野，也增加了练习的趣味性，使学生知道数学和生活是紧密相连的。

(六)总结

及时进行课堂总结能够让学生建构起数学概念体系。教师对这个环节是否重视，会直接影响学生掌握数学概念的程度。

一是概括式总结。进行概括式总结时，教师提出的问题需要清晰明确。例如，教师可以提问以下问题：本节课收获了哪些知识？你是怎么学会这些知识的？这些问题可以促使学生简单回顾知识，加深理解。

二是设疑式总结。进行设疑式总结时，教师要根据教学实际情况，有针对性地提出一些有启发、有趣味的数学问题，并将这些问题留给学生，让学生再思考和验证，以此激发学生主动探索数学的意识。例如，教师可以做如下设计。

师：咱们班女生有24人，能不能说出24的因数有哪些？24的倍数呢？

生：24的因数有1、2、3、4、6、8、12、24；24是这些数的倍数。

师：因数说出来了，但24的倍数没讲，同学们课后思考一下，明天课上告诉老师24的倍数是多少。

三是解惑式总结。课前提出的问题可以激发学生强烈的求知欲和好奇心，课中回答课前提出的问题，可以让学生加深记忆，获得更好的学习效果。例如，教师可以提出以下问题：因数与倍数的概念是什么？它们之间有什么关系？因数与倍数研究的是哪些数？这里的倍数与之前学过的倍有什么不同？

三、结语

教学概念时，教师应重视引导学生进行数学材料的阅读，培养学生的问题意识，使学生在探究中建立初步的概念感知，在课堂上敢于表述和交流自己的发现并规范自己的语言表达，在课后练习题中巩固对概念的认识，最后进行总结，深化概念的习得。此外，教师在数学概念教学中，需要结合具体学情和概念的特点，灵活设计教学环节，合理运用“六步法”，让学生在掌握数学概念的同时，对数学产生兴趣，提高数学素养。