全空间上类p-Laplacian方程解的存在性
2022-03-31丁玲
丁 玲
(中国人民解放军陆军炮兵防空兵学院 基础部,安徽 合肥 230031)
1 预备知识
在全空间RN(N≥3)上考虑类p-Laplacian方程

(1)
的解,其中2≤p 陈祖墀等[1]在有界光滑区域Ω⊂RN(N≥3)中研究了类p-Laplacian方程的特征值问题,证明了以下两个有趣结果: 假设 A3)NB(r)-B′(r)r关于r是严格单调递增的. 定理1设A1)—A3),f1)—f2),V)成立,则方程(1)存在非平凡解u(x)∈W1,p(RN). 记 由变分原理,寻求方程(1)的弱解可归结为寻找 (2) 引理1设A1)—A3),f1),V)成立,则由(2)式定义的泛函I∈C1(E,R). 步骤1证明IA是Gateaux可微的.证明过程见文献[1]. 步骤2证明I′A是连续的,从而IA是Frechet可微的. (3) 对于(3)式右边第1项,有 →0. 对于(3)式右边第2项,因为a0≤a≤T,且Dum→Du,a.e.x∈RN,故由Lebesgue控制收敛定理,得 这就证明了I′A在u连续,从而IA是Frechet可微的,即有IA∈C1(E,R). 步骤3对于泛函I中的其他积分项,可类似IA的证明,从而I∈C1(E,R). 接下来证明能量泛函I(u)具有山路几何结构. 引理3存在v∈E,使得I(v)<0. 由引理2和3,以及山路定理[7-8]知,对 其中:c为常数;Γ={γ∈c([0,1],E):γ(0)=0,γ(1)≠0,I(γ(1))<0},存在(PS)序列{um}⊂E,即有I(um)→c,I′(um)→0(m→∞). 命题1(PS)序列{um}是有界的. (4) 计算可得 I′(um)φ→I′(u)φ. (5) 为此,先证明下面的梯度几乎处处收敛. 命题2设{um}为泛函I的有界(PS)序列,则Dum→Du几乎处处于RN中. 证由E=W1,p(RN)及延拓定理,可取紧集K′⊂⊂K⊂RN.设光滑函数φK:RN→R满足0≤φK≤1,并且φK=1在K′上,φK=0在RNK上.取φ=φK(um-u).由于um→u几乎处处于K中,um→u于Ls(K)(1≤s (6) 由A2)知 (7) (8) 结合(6)—(8)式,易知Dum→Du几乎处处于K中.利用一列紧集Ki(i=1,2,…)覆盖RN,则由可数可加性知,Dum→Du几乎处处于RN中. 下面证明(5)式.易知 等式右边第2,3项显然收敛于零,对于第1项,有 而在BR上,由于Dum→Du几乎处处成立,故由Egrov定理,得 从而可知Ⅳ→0.另一方面,由Lebesgue控制收敛定理易知Ⅴ→0.从而(5)式成立. 下面证明u≠0,即u是方程(1)的非平凡弱解.利用反证法.假设u=0.考虑泛函I∞:E→R, 命题3{um}是泛函I∞在水平的(PS)序列. 命题4存在R>0,α>0,使得 证假设结论不成立,则由集中紧性原理[8-9]知,um→0于Ls(RN)(p 从而有 即um→0于E以及Lp(RN)中,从而由I的定义,有I(um)→0,这与I(um)→c>0矛盾. 由命题4,存在α>0,R>0以及序列{yn}⊂RN,使得 (9) 例1考虑方程 解的存在性,其中p≥2,N≥3,p 从而有 关于r是单调递增的.故由定理1知方程存在一个非零解.


2 主要结果
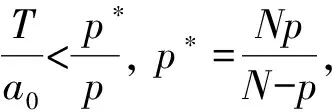
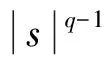
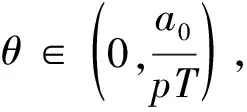

3 定理1的证明
3.1 能量泛函分析

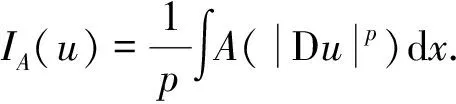
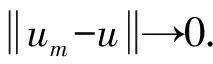






3.2 (PS)序列分析


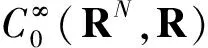

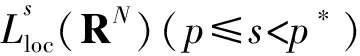
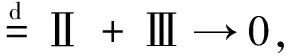


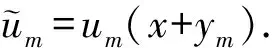







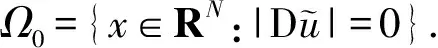



4 例子

