多层圆线圈在电磁计算中全空间磁感应强度B的分布
2016-04-12Thefullspacedistributionofmagneticinductionintensityofmultilayercircularcoilsinelectromagneticcalculation
The full space distribution of magnetic induction intensity B of multi layer circular coils in electromagnetic calculation
周 敏,田大庆,李小润,刘 畅ZHOU Min, TIAN Da-qing, LI Xiao-run, LIU Chang(四川大学 制造科学与工程学院,成都 610065)
多层圆线圈在电磁计算中全空间磁感应强度B的分布
The full space distribution of magnetic induction intensity B of multi layer circular coils in electromagnetic calculation
周敏,田大庆,李小润,刘畅
ZHOU Min,TIAN Da-qing,LI Xiao-run,LIU Chang
(四川大学 制造科学与工程学院,成都 610065)
摘要:励磁类线圈在线圈通电流时在线圈内外空间产生相应的磁感应强度,如亥姆霍兹线圈。从毕奥-萨伐尔定律出发,通过矢量运算和几何关系,利用多层圆线圈磁场的对称性推导出全空间磁感应强度分布的积分表达式,并运用Ansoft Maxwell软件仿真模拟磁场的分布。
关键词:多层圆线圈;全空间;磁感应强度;Ansoft Maxwell;仿真模拟
0 引言
对于抓取本身具有磁性的微小尺寸物体,由于尺寸极小的原因,通常情况下,用机械方式和真空吸取难以实现,只有用电磁吸取的方式,但物品重量极小和自身带有磁性,故不能采用传统的电磁铁吸取,直接由多层圆线圈和非导磁材料组成的方式来实现,且线圈材料需为漆包铜线。在该电磁计算中要涉及到多层圆线圈的磁感应强度的计算,在匝数有很多时就需要将绕线分别排布在多层之中,即绕线在径向有定的厚度。很多论文对单层载流圆线圈全空间的磁场分布进行了讨论,但对多层圆线圈的全空间的磁场分布讨论较少。本文应用多层圆线圈的等效半径和毕奥-萨伐尔定律计算了多层圆线圈在空间任意点的磁感应强度,并运用Ansoft Maxwell软件分析模拟了磁场的分布。
1 多层圆线圈的等效半径
我们设多层线圈是密绕的,即相邻两层线圈之间没有间隙。其中最内层线圈的半径为r1,最外层线圈的半径为r2,绕制线圈所用漆包线的直径为d,显然根据可求出多层线圈的层数,N匝绕线均匀地分布于厚度为r2-r1的圆环状空间内,线圈内的电流为I。
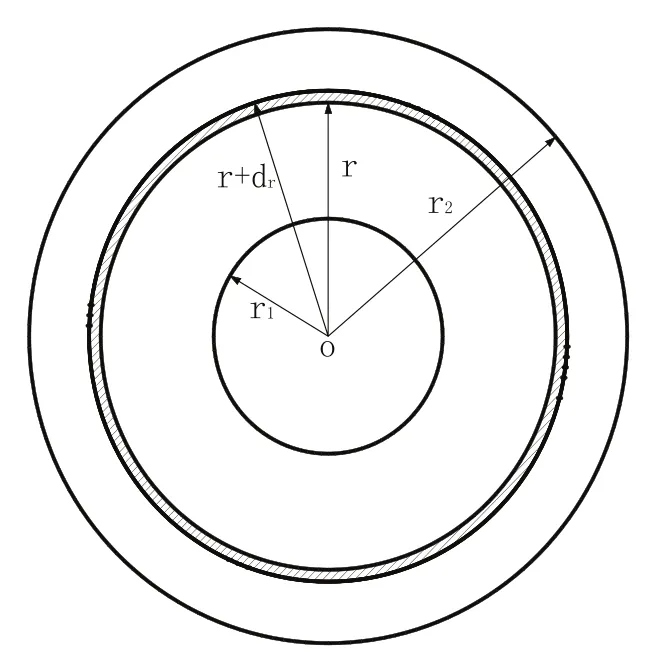
图1 等效半径推导示意图
任取半径r(r1<r<r2)。做半径为r的圆,在其外做半径为r+dr的圆,在这微环内绕线匝数为,u0为真空磁导率,其值为如图1所示。它对O点磁感应强度为:

整个线圈在中心O点产生的磁感应强度为:

设等效半径为Rd,则B0应与半径为Rd,电流为NI的匝线圈在中心O点产生的磁感应强度相等,由此可得等效半径为:
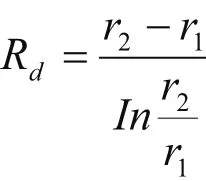
2 应用毕奥-萨伐尔定律求解多层载流圆线圈在全空间的磁感应强度的分布
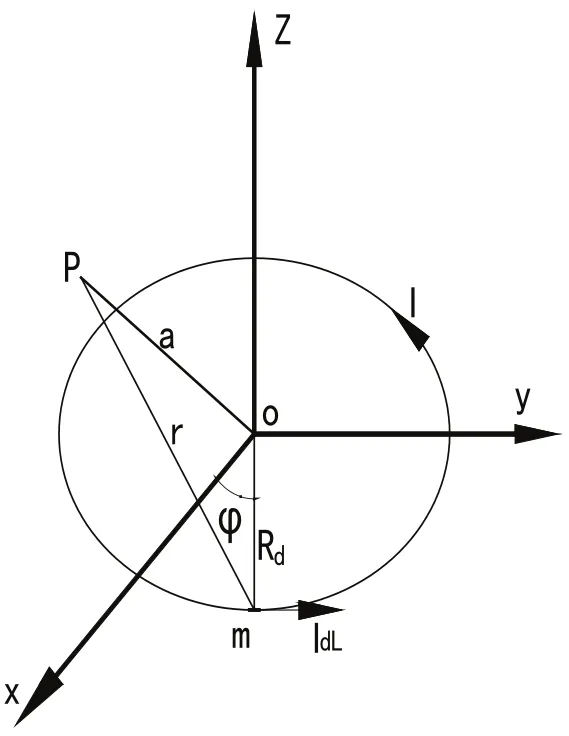
图2 计算载流圆线圈磁场分布的示意图



其中:
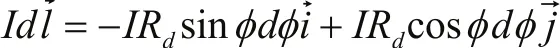
则:

所以P点处的磁感应强度为:
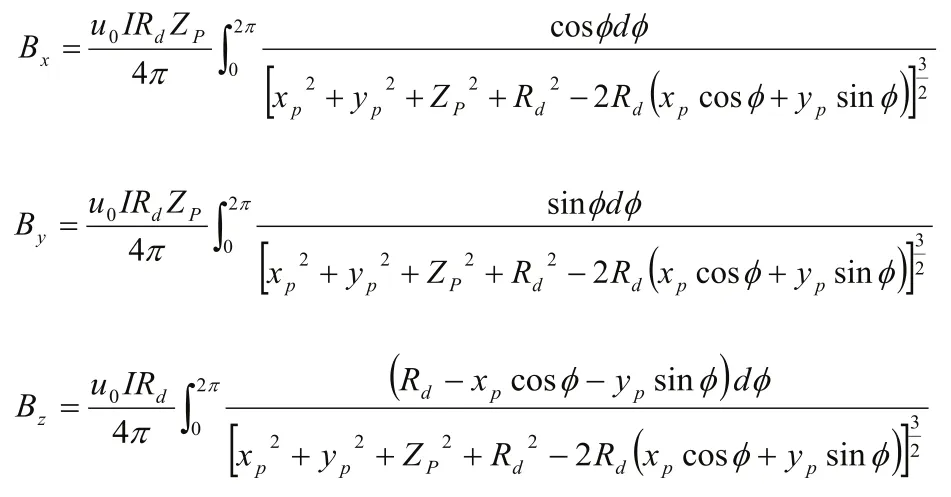
1)当点P在多层圆线圈的轴线上时,P点坐标为(0, 0,Zp):

等效半径:

2)当P点在多层圆线圈所在o-xz平面上时,P点坐标为(xp,0,Zp),此时:
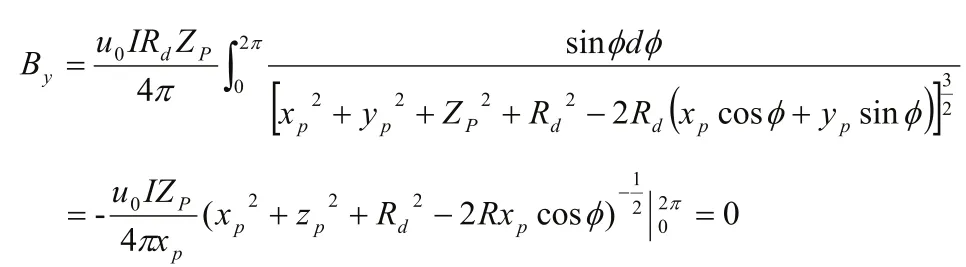
由于By=0,磁场在该方向的分量为零,P点的选取
【】【】
是任意的,由于多层圆线圈具有对称性,所以多层圆线圈外任意点的磁场在垂直于原点与P点的连线和多层圆线圈的轴线组成的平面的方向上的分量为零。
3 运用Ansoft Maxwell模拟多层圆线圈在全空间的磁感应强度分布
本文研究多层电磁圆线圈在恒定电流状态下的磁场强度分布,稳态下线圈产生的磁场适用于Maxwell 2D静态磁场的magnetostatic方法分析。为简化分析,假设电阻为线性,与温度无关。假设r1=0.4mm,r2=0.8mm,总的安匝数为1A,即IN=IA,线圈材料为漆包铜线。在Ansoft Maxwell图形编辑环境下,建立线圈、空气等二维截面模型如图3所示。

图3 线圈模型
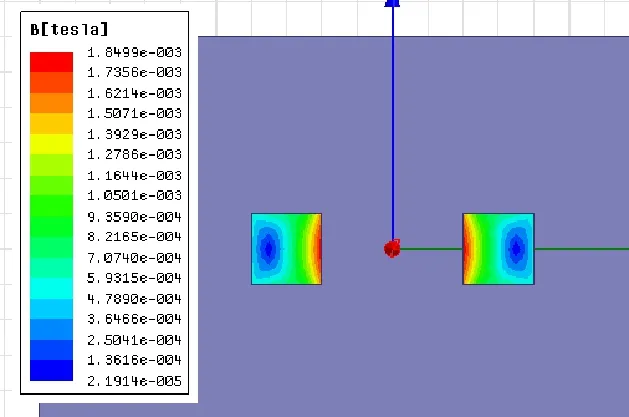
图4 多层载流圆线圈磁密B标量分布
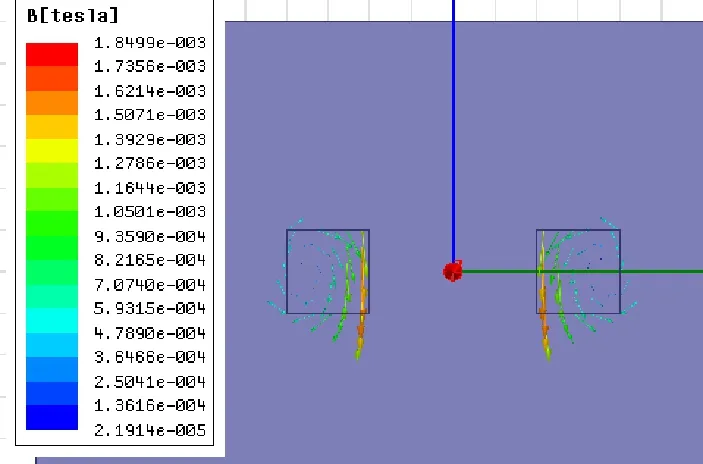
图5 多层载流圆线圈磁密B矢量分布
通过图4和图5可以看出,多层载流圆线圈在空间磁密B的分布是不均匀的,靠近中心处磁密较大,而随着半径的增加外侧的磁密逐渐减小,这个分布规律与理论是致的。同时验证了多层圆线圈外任意点的磁场在垂直于原点与P点的连线和多层圆线圈的轴线组成的平面的方向上的分量为零这结论。
4 结束语
参考文献:
[1] 张欢,马全喜.多层圆线圈在电磁计算中的等效半径[J].物理通报,2010(10):17-18.
[2] 李春明,刘承师,张俊峰.计算载流圆线圈空间磁场分布的方法[J].辽宁工学院学报,1999(1):62-66.
[3] 詹树军.载流圆线圈外空间任意点磁场的研究[J].毕节学院学报,2012(8):112-120.
[4] 罗宏超,蔡敏.圆电流全空间磁感应强度B的分布[J].沈阳航空工业学院学报,2006(23):79-80.
[5] 刘保义,张明霞.圆环电流在全空间形成的磁感应强度分布[J].天水师范学院学报,2009(29):65-66.
作者简介:周敏(1990 -),男,四川南充人,硕士研究生,研究方向为机电控制技术和智能控制。
收稿日期:2015-11-25
中图分类号:TM153.1献标识码:A
文章编号:1009-0134(2016)03-0018-03
