桨叶重力作用下的旋翼载荷标定测试技术

焦帅克， 耿丽松， 王泽峰， 郑甲宏

(中国飞行试验研究院，陕西 西安 710089)

0 引 言

自从直升机首次被发明出来，直升机应用领域广泛，虽然全世界几万架直升机遍布于军用、民用各个领域，但是直升机技术的潜力仍被开发得很少，与固定翼飞机技术相比仍有很大差距。飞机飞行寿命偏低，安全性不高是约束直升机技术发展的因素之一。旋翼作为直升机的核心部件之一，其主要为直升机提供升力，从而使直升机稳定的飞行[1]。因此，旋翼系统的安全性影响着直升机的飞行安全。直升机旋翼系统工作时，其有挥舞、摆振、扭转等多个运动自由度，这些自由度之间存在着复杂的耦合关系，旋翼系统会受周期载荷的作用，从而引起桨叶的疲劳，影响直升机的飞行安全[2-4]。因此，旋翼载荷测量是直升机技术必不可少的研究课题，如何准确地测量出直升机的挥舞、摆振、扭转等载荷显得尤为重要[5]。

直升机部件载荷测量技术已经十分成熟，许多直升机部件的变形已经能够准确测量[6-7]，直升机的旋翼部件也是其测量的一部分。国内外在直升机桨叶载荷测量技术方面有所研究，大多数对旋翼系统载荷测量一般采用电阻应变计法[8]，通过标定载荷和电桥输出的关系，得到标定曲线，将实测数据带入该曲线反算出飞行载荷[9]。由于飞行载荷中存在挥—摆耦合，2000年，Bernard Y[10-11]针对某型直升机通过数值解耦的方法将挥舞、摆振载荷分离出来；2001年，余洵等[12]提出了一种高效的载荷标定方法，通过理论分析的方法，认为找出“最佳角度”更能减少载荷标定的工作量；2009年，刘正江等[13]对模型桨叶载荷进行标定研究，为实际桨叶载荷标定奠定基础；2010年，余洵[14]对比分析了“数值解耦”和“物理解耦”方法的优劣性；2012年，韩树旺等[15]系统描述了飞行载荷的标定方法，但未曾分析旋翼重力在载荷标定过程中的影响；2014年，李永寿等[16]将“物理解耦”的方法应用到实验上；2018年,王泽峰等[17]提出了一种桨叶预扭角的确定方法。

该文在以上研究结果的基础上，考虑分析了桨叶重力对载荷标定实验的影响，并为后续载荷标定实验中“预扭角”确定的过程中出现了一种“预扭角”随旋转方向的不同而不同的“伪现象”进行了解释分析，并对“错误”数据进行了理论和实验修正，说明了载荷标定过程中桨叶的重量不可忽略，否则将会影响标定曲线的准确性，进而影响飞行载荷数据测量的准确性，影响直升机的飞行安全。

1 应变片的选择与粘贴

为了测得更为准确的主桨叶的载荷数据，选取合适的应变片尤为重要。该文选用的是中航电测生产的应变片，型号为BA350-2AA(9)-G150-JQC，相关参数如表1所示。

表1 应变片的相关参数

根据设计所给出的贴片剖面位置及类型，如图1和表2所示。可知，共有8个剖面需要贴片，其中柔性梁上（AreaⅠ）有4个剖面（r=185 mm，r=265 mm，r=305 mm及r=550 mm剖面）；另外4个剖面位于桨叶上（r=650 mm，r=845 mm，r=970 mm及r=1 160 mm剖面）；r=1 500 mm为加载剖面。挥舞方向的弯矩载荷和摆振方向的弯矩载荷如图1（b）所示。在柔性梁的r=185 mm，r=265 mm及r=305 mm剖面的中心位置的上下表面分别贴上一组平行片并组成全桥用于柔性梁挥舞弯矩的测量；柔性梁的前后表面分别贴上一组平行片并组成全桥用于柔性梁摆振弯矩的测量；在柔性梁r=550 mm剖面上下位置分别贴上一组扭矩片并组全桥用于柔性梁的扭矩测量。由桨叶的结构可知，C字梁为主要承受挥舞载荷的部件，即桨叶的弦线处，应在桨叶的r=845 mm，r=970 mm及r=1 160 mm剖面的上下表面分别贴上一组平行片并组成全桥用于桨叶挥舞弯矩的测量，但由于红色区域（Area Ⅱ） 内无法进行贴片，故r=845 mm和r=970 mm的贴片位置需尽量靠近弦线处；由于桨叶的前后缘位置很薄无法进行贴片工作，同理，这3个剖面的摆振片的贴片位置应尽量靠近桨叶的前后缘；在桨叶r=560 mm剖面上下位置分别贴上一组扭矩片并组全桥用于桨叶的扭矩测量。

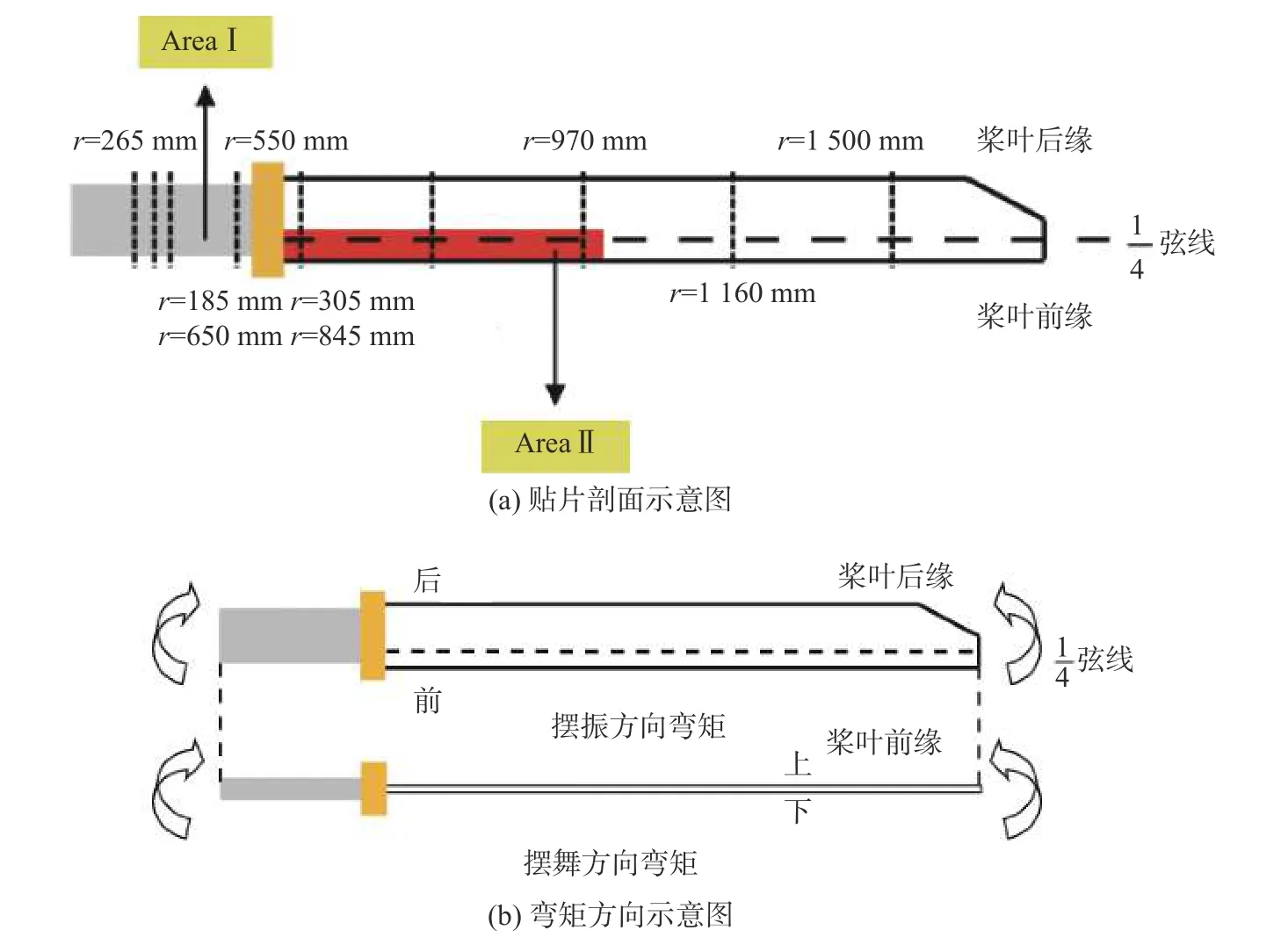
图1 贴片位置及弯矩载荷方向示意图

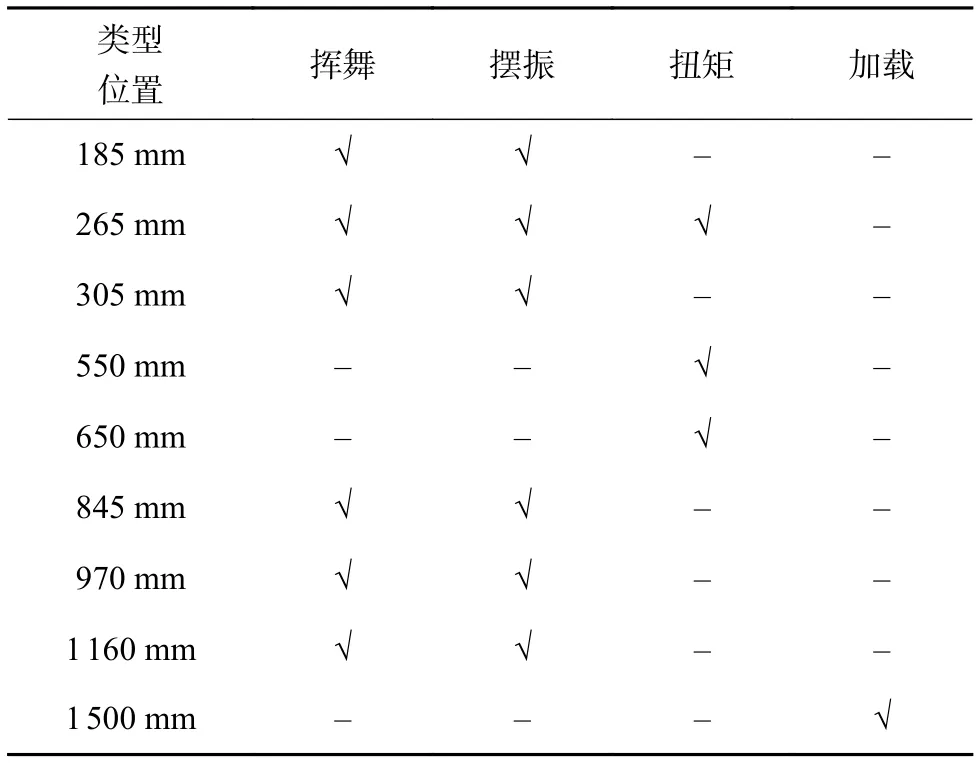
表2 贴片剖面位置与贴片类型

表2中每个剖面的类型分为四种，第一种代表该剖面贴有挥舞片，简称“挥舞”；第二种代表该剖面贴有摆振片，简称“摆振”；第三种代表该剖面贴有扭矩片，简称“扭矩”；第四种代表该剖面为加载剖面，简称“加载”。如若该剖面有某一类型的情况，则用“√”表明，如若没有用“-”表明。

2 预扭角的测量

2.1 测试原理和装置

直升机桨叶在正常工作状态下，会存在挥舞运动和摆振运动。通常情况下，挥舞运动和摆振运动会相互影响，即两种运动会相互耦合。故如何准确测出桨叶某个剖面的挥舞弯矩和摆振弯矩尤为重要。桨叶载荷标定是实测桨叶载荷最重要最基本的一个步骤，由图2可知，若标定桨叶摆振载荷时，当桨叶竖直放置时，加载力的方向与剖面的中性轴存有一定的夹角 α，将角 α称为预扭角，则加载力F不仅会使该剖面产生摆振弯矩还会产生挥舞弯矩。

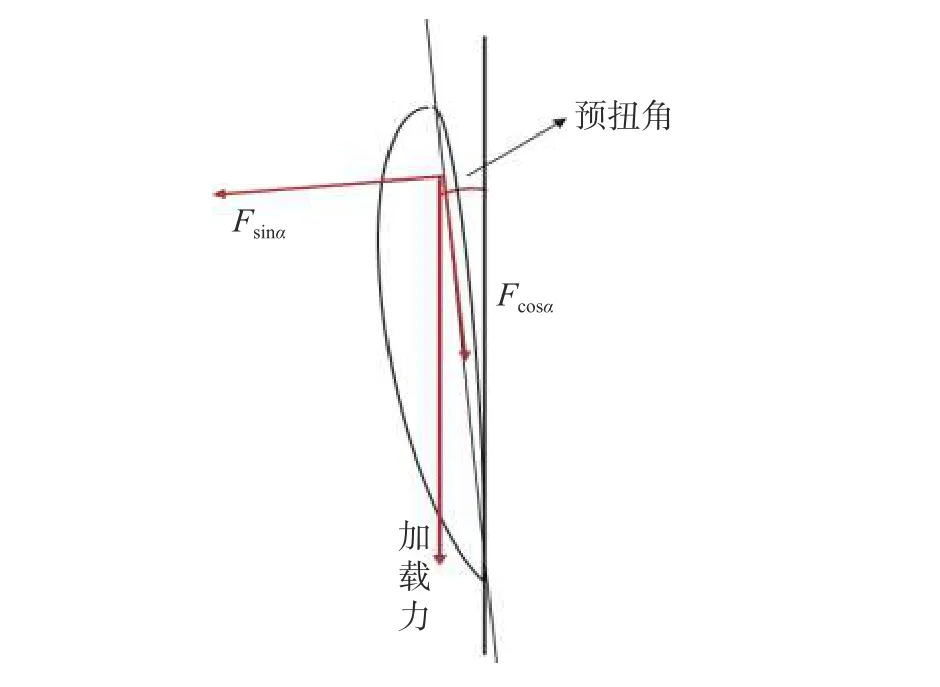
图2 摆振标定加载

设加载端距计算剖面的距离为d，则该剖面的摆振弯矩为Mb=Fcosα·d，挥舞弯矩为Mh=Fsinα·d≈Fα·d。若想要得到更为准确的标定曲线则需要知道预扭角 α。

测量装置如图3所示，部件①是转动轴，用于调节加载方向与剖面中性轴之间的夹角；部件②是角度测量仪，用于测量旋转轴转过的角度；③是待测试件，某型直升机的桨叶；④是桨叶根部的固定夹具；⑤是加载夹具。

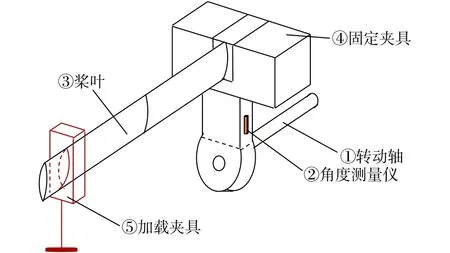
图3 测试装置

一般预扭角都较小，基本都小于10°。本文桨叶自由端加载均为5 kg的砝码，并以0°为起始点，2°步长旋转转动轴，记录每个角度下的挥舞应变的输出值，当旋转角度等于预扭角的大小时，中性轴与加载力的方向垂直，那挥舞应变理论上应为零，此时便能测出预扭角的大小。

2.2 未考虑重力的测量结果

桨叶载荷标定方法中预扭角的确定过程若未考虑过桨叶自重对预扭角确定的影响会导致测量结果出现偏差，且会出现预扭角随旋转轴的旋转方向不同而不同的伪现象，如图 4 所示。图 4（a）（b）（c）是3个剖面未考虑重量影响下的曲线，图4（d）表明预扭角两次实验明显差别过大。

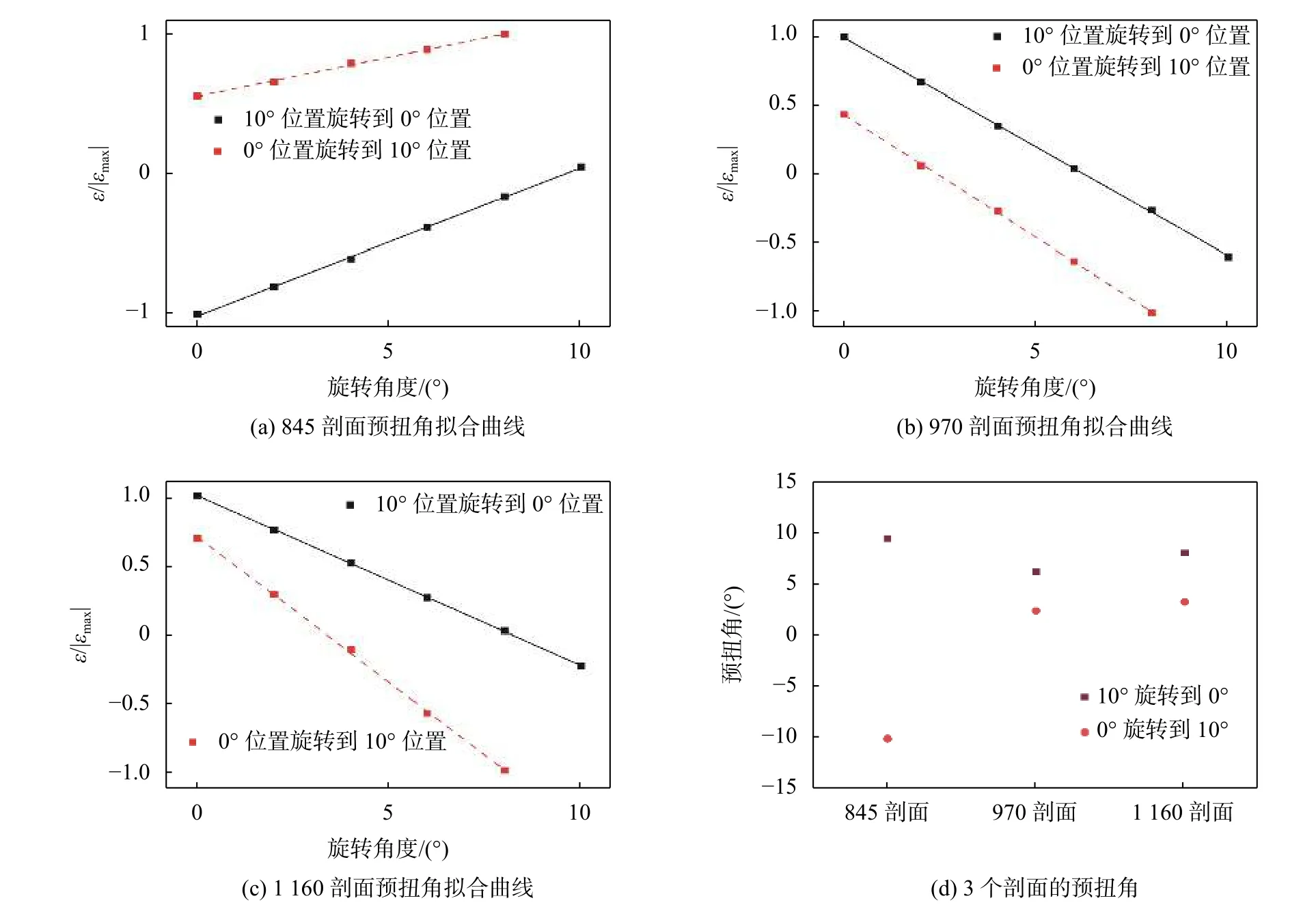
图4 三个剖面的扭转角测试分析图

为了消除重力的影响，可以从两个方面入手，一方面，从理论上分析，计算出重力的影响，然后进行数据修正；另一方面是从实验入手，每转过一个角度记录一次零位（进行清零操作）。

2.3 理论修正数据

第一次实验从10°位置转到0°位置，如图5（a）所示。由于只在初始位置（10°）进行了一次清零操作，这时每个角度下对应的真实应变值可由公式（1）表示；同理，第二次实验，如图5（b）所示，可得到公式（2），其中 εi代 表i°时的真实应变， ε1i代表第一次实验i°时，测量仪器的输出值， εi°重力代表i°时重力产生的应变值。

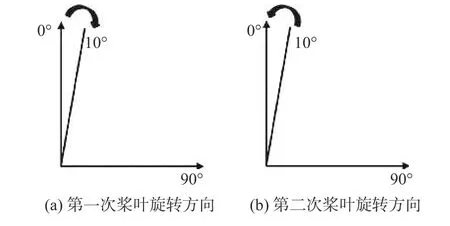
图5 桨叶旋转方向

用（1）式减去（2）式可得公式（3）：

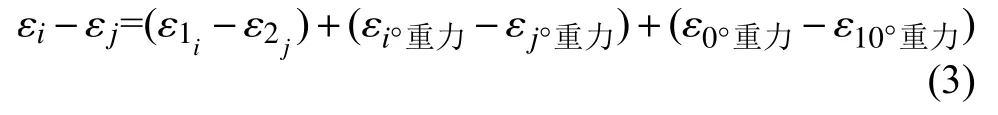
令i=j，式子（3）变为式子（4）：

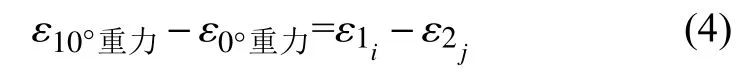
由于当F值一定时，近似有Mh∝α，且 ε ∝Mh，故 ε ∝ α，则得公式（5）：

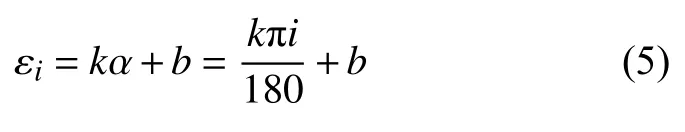
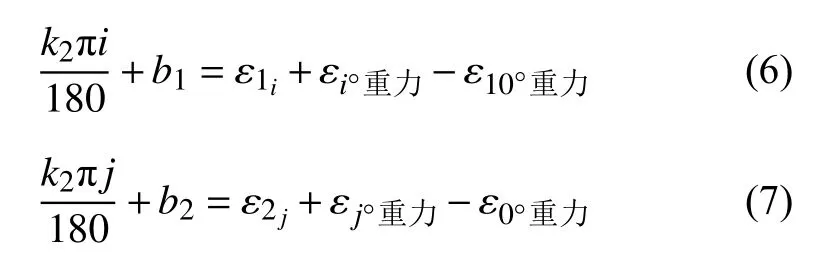
令i=10可得，；令i=0可得，b1= ε10+ε0°重力-ε10°重力则得：

同理，得：

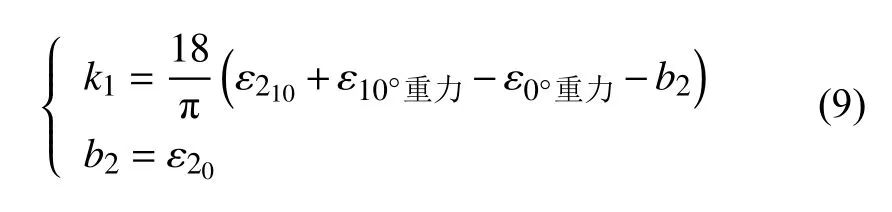
根据公式（4）计算得到3个剖面的差值，并做平均处理，然后根据计算结果代入公式（8）（9）计算，计算结果如表3所示，3个剖面的预扭角如图6所示。从图5可知经过修正后的数据不再受旋转方向的影响。预扭角是否计算准确需要通过实验修正来验证。

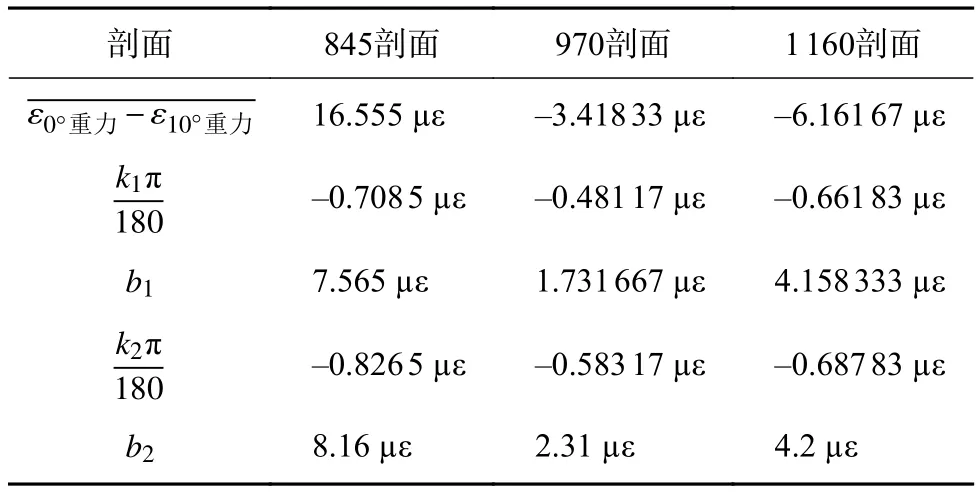
表3 计算结果

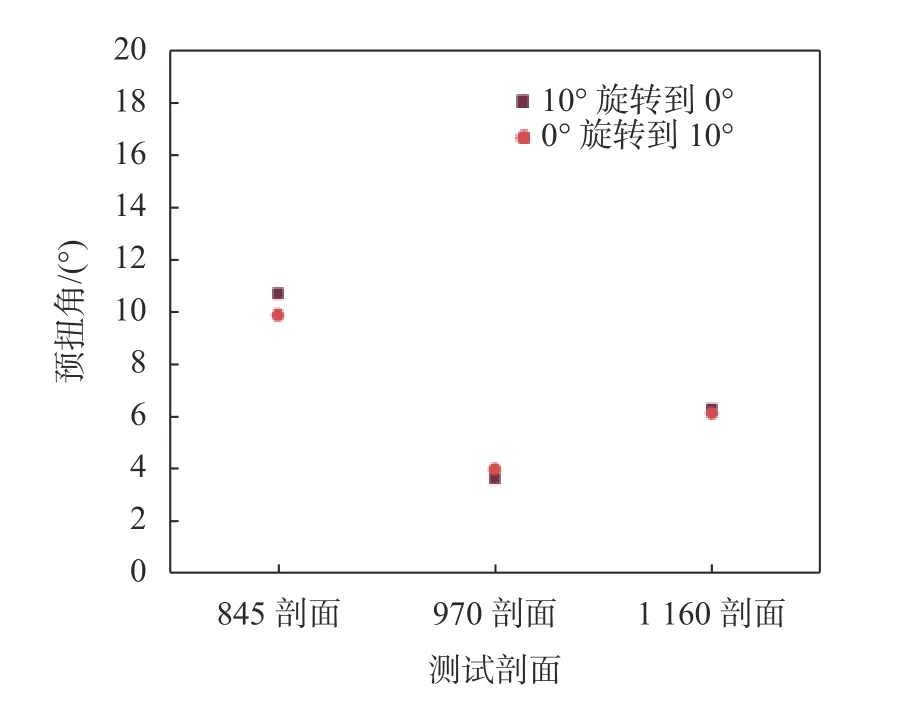
图6 数据修正后的预扭角

2.4 实验修正数据

实验修正也按照图5方式进行两次实验，每转过一个角度就进行清零操作计算结果如图7所示。图7（a）（b）（c）分别是 3 个桨叶剖面的预扭角拟合曲线，图7（d）是两次数据修正结果和两次实验修正结果的比较，可以发现四次结果基本吻合，结果见表4。数据修正和实验修正结果相互印证，这说明经过修正后的数据有效且具有一定的准确性，可供后面标定实验使用。修正后的扭转角存在一定偏差是可能是因为桨叶的不均匀性以及在数据修正时候采用了线性插值引起了一定的误差。

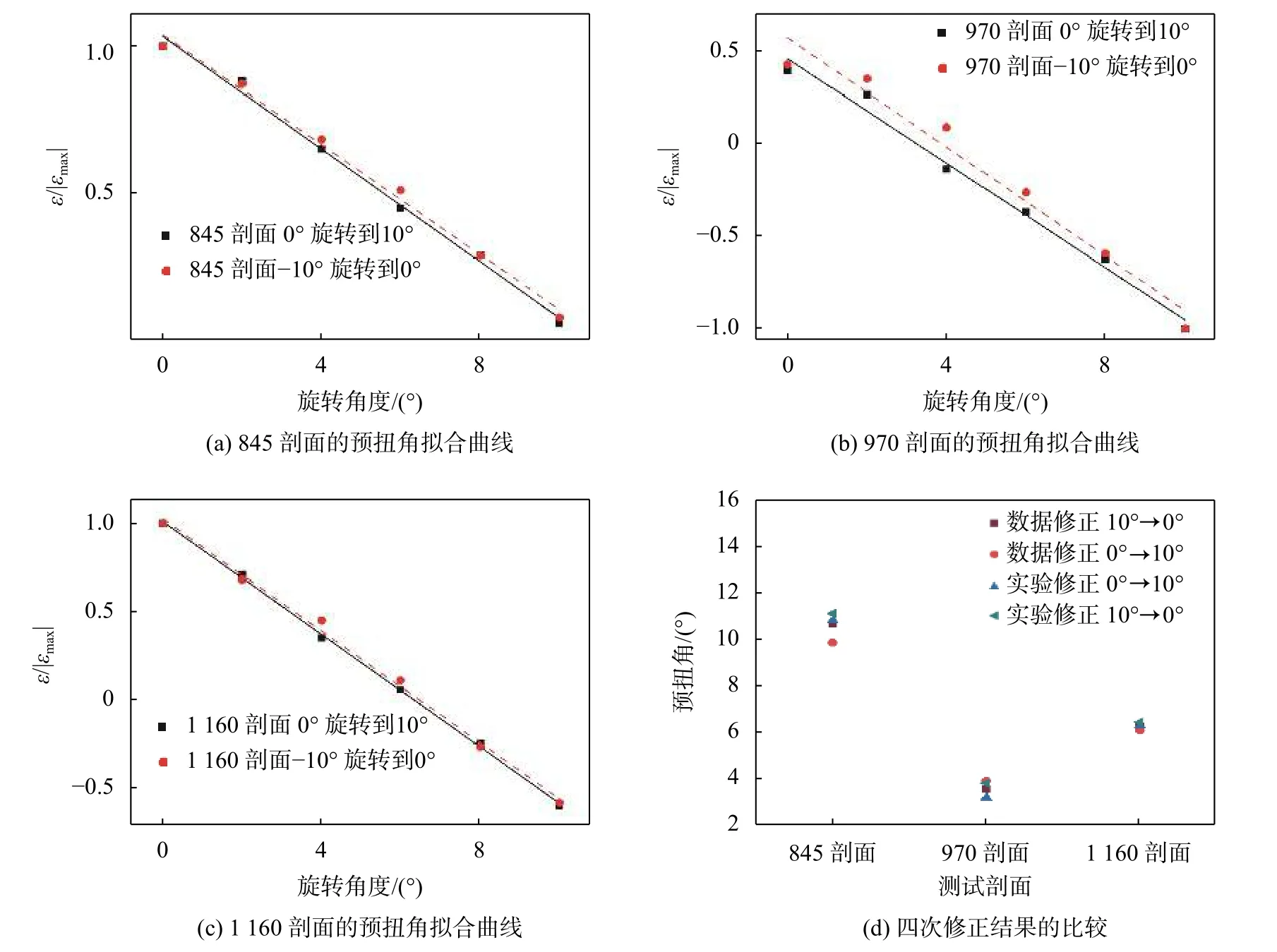
图7 三个测试剖面的结果分析图

表4 三个剖面四次扭转角修正结果

3 摆振片的选择

由第二小节内容可知摆振片无法粘贴在桨叶的两侧，只能尽可能贴在靠近桨叶的前后缘处。首先在桨叶的上表面贴四分之一弦线处贴上一个应变单片，作为应变全桥桥路的1号应变片，下表面对称位置贴一个应变单片作为2号应变片；靠近桨叶后缘处，以1 cm为梯度布片，上表面布3个应变片，下表面布3个应变片，从这6个应变片中找出应变桥路中的2,4号应变片，如图8所示。

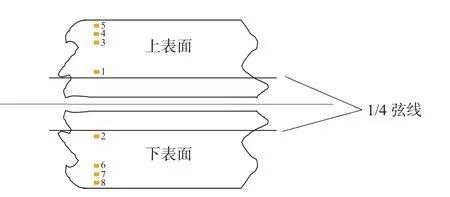
图8 摆振片贴片示意图

按照文献[12]给出的方法进行摆—挥解耦，挥舞加载载荷为 2 kg，摆振方向施加载荷 6 kg，，当挥舞方向加载产生的应变比上摆振方向加载的应变小于“耦合系数”5%时，即认为解耦成功，否则需根据测试结果重新解耦[16]。845剖面测量结果如表5，表6所示，其余2个剖面不再展示。

表5 845剖面摆振方向测量结果

表6 845剖面挥舞方向测量结果

由表7可知845剖面的摆振片的选片结果为1，2，3，5，其余两个剖面选片过程与845剖面选片同理。

表7 选片结果

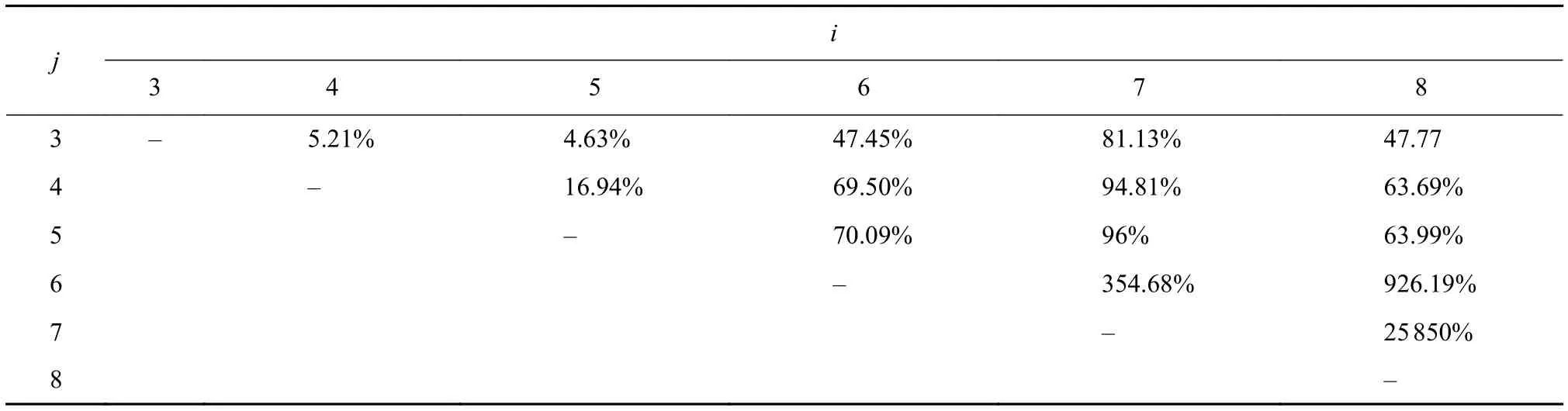
表7 选片结果

j i 3 4 5 6 7 8 3 - 5.21% 4.63% 47.45% 81.13% 47.77 4-16.94% 69.50% 94.81% 63.69%5 70.09% 96% 63.99%6-354.68% 926.19%-7 25 850%8--

4 标定结果

桨叶和柔性梁的上的挥舞片、摆振片、扭转片均贴好后，进行标定试验，标定结果如图9和图10所示。由图可发现桨叶和柔性梁标定曲线均呈良好的线性，这表明把桨叶等效为弹性梁是基本正确的，同时侧面反映了标定结果的可靠性。同时，发现相同载荷状态下桨叶越靠近根部桨叶所受的挥舞和摆振应变越大，这与弹性力学中的观点一致；而柔性梁265剖面的受载最为严重，这与柔性梁的结构和材料有关。

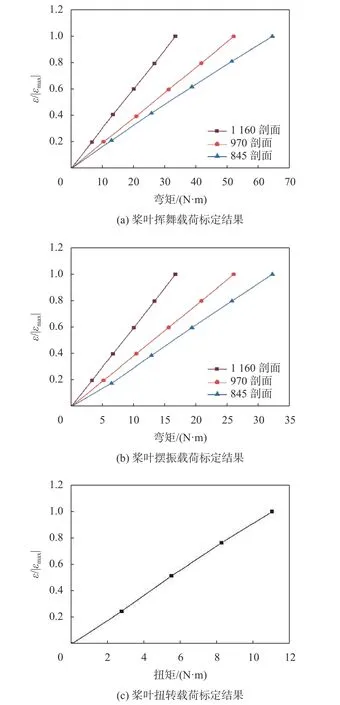
图9 桨叶载荷标定结果

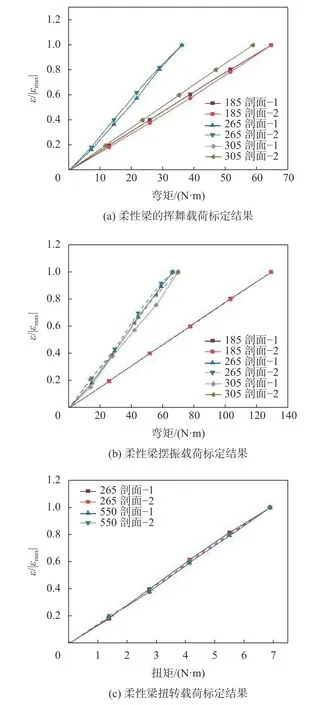
图10 柔性梁标定结果

5 结束语

该文在标定实验过程中发现了一种伪现象，通过分析发现是由于桨叶重力的作用造成了这一现象的产生，这表明在标定过程中桨叶的重力影响是不能忽略的。该文从理论分析和实验测量两方面入手，对数据进行修正，结果表明理论分析和实验测量基本吻合，理论和实验相互印证，这表明了测量结果的准确性。最后，通过载荷标定方法给出了旋翼柔性梁和桨叶的标定曲线，曲线呈现良好的线性结果，该结果与理论分析一致，这也说明了标定结果具有极高的可信度，为未来进行飞行载荷测量提供依据。