柱面统计最优近场声全息参数对比研究

陈 璐， 郭世旭， 王月兵， 郑慧峰

(中国计量大学计量测试工程学院，浙江 杭州 310018)

0 引 言

随着航海军事能力逐渐重视，在反潜战、水下侦察与后勤支援等军事领域中水下航行器的性能起到重要作用。若要实现成为航海军事强国，研发出能监测到对方水下航行器，对自身设备进行噪声识别并做出针对性降噪工作，隐匿我方位置信息的声源定位分析技术尤为重要。近场声全息（near-field acoustical holography, NAH）作为近场内噪声定位、声场可视化的重要算法，国内外对其开展了大量研究。

近场声全息是声学研究中的一种极其重要的声场推算方法，最早由Williams提出，并根据空间声场变换进行了大量实验应用[1-3]。统计最优近场声全息（statistically optimized NAH, SONAH）作为声全息技术中的重要算法，因其优秀的声源重构能力被广泛研究。李卫兵等人利用双全息面对统计最优算法进行改进，实现声场分离技术[4]。张永斌提出了一种平面波优化方法，对传递函数进行改进，提升了重构精度[5]。赵报川通过多种波函数组合得到声场传递函数，提高了声场重构的精度[6]。熊久鹏提出二维平面声压重构技术来提高声场测量效率[7]。陈新宁对胶囊状壳体进行的仿真和实验分析，验证了基于近场声全息的反射场重构的可行性[8]。杨枭杰在重构算法中引入滤波算法，对比了三种滤波对边缘误差的抑制效果[9]。

本文在柱面统计最优近场声全息算法基础上对比研究了基于声压与振速进行声场重构时分别在声源频率与重构距离变化情况下各自的重构精度与重构效果，利用仿真分析与实验验证，证明了统计最优近场声全息算法的可靠性，以及基于振速矢量信息进行声场重构时在声源分辨与声场还原的优势。

1 基于统计最优的近场声全息技术

统计最优近场声全息是局部近场声全息算法的一种，由于不涉及傅里叶变换，因此有效的解决了基于傅里叶变换的近场声全息中存在的窗效应和卷绕误差。但算法中参数受矩阵求逆的影响较大，因此矩阵中奇异值较小项成为误差主要来源。

通过以上分别基于声压或振速重构声场声压的统计最优近场声全息算法，可以得到近场区域内任意位置的声场信息。由于算法重构精度受外界条件影响多，其中声源频率与重构距离尤为重要，下文将从这两个方面分别对声压与振速重构情况进行对比，分析比较两种重构方式在不同工况情况下的变化趋势。

2 近场声全息仿真与结果分析

建立有限元仿真模型，将激振源所在柱体设为柱坐标中心，柱体中轴线为柱坐标的z轴，柱体半径为0.2 mm，有效振动柱面高为0.5 mm，柱体内壁位于（0.2 mm，0°，0.15 mm）与（0.2 mm，0°，0.35 mm）处有两个同频同相向外振动的激振点，重构柱面半径r0=0.25 m，全息柱面半径分别为r1=0.30 m，r2=0.35 m，r3=0.40 m，信号采集范围与柱面共形且与有效振动柱面等高，轴向采样点数为21个，周向采样点数为16个。仿真环境设为声速c=1 500 m/s，水密度 ρ=1 000 kg/m3的水域，模型采用边界元，因此可以忽略实验环境中的水面和池壁反射。

为了便于算法重构效果比较，定义声场重构误差为：

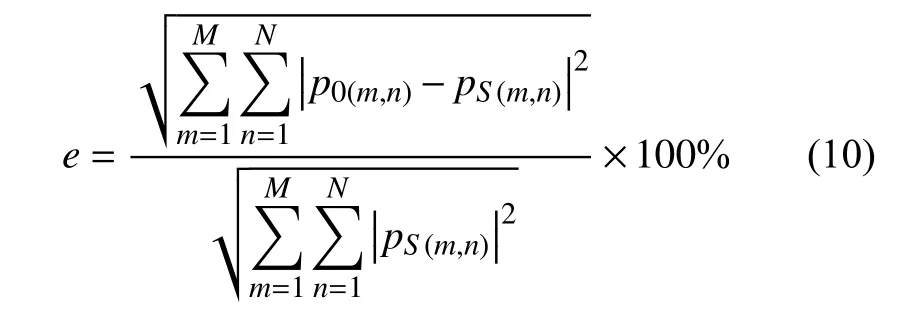
其中，p0(m,n)与pS(m,n)分别表示重构面的测量声压与计算声压。

2.1 声源频率对两种算法重构精度的影响

修改仿真条件中声源参数设置，声源与柱体参数不变，重构柱面半径r0=0.25 m，全息柱面半径r1=0.30 m，分别在声源为100 Hz到1 000 Hz时对算法的重构精度进行计算，重构误差随声源频率变化趋势如图1所示，“+”表示用声压重构声压算法，“*”表示用振速重构声压算法。

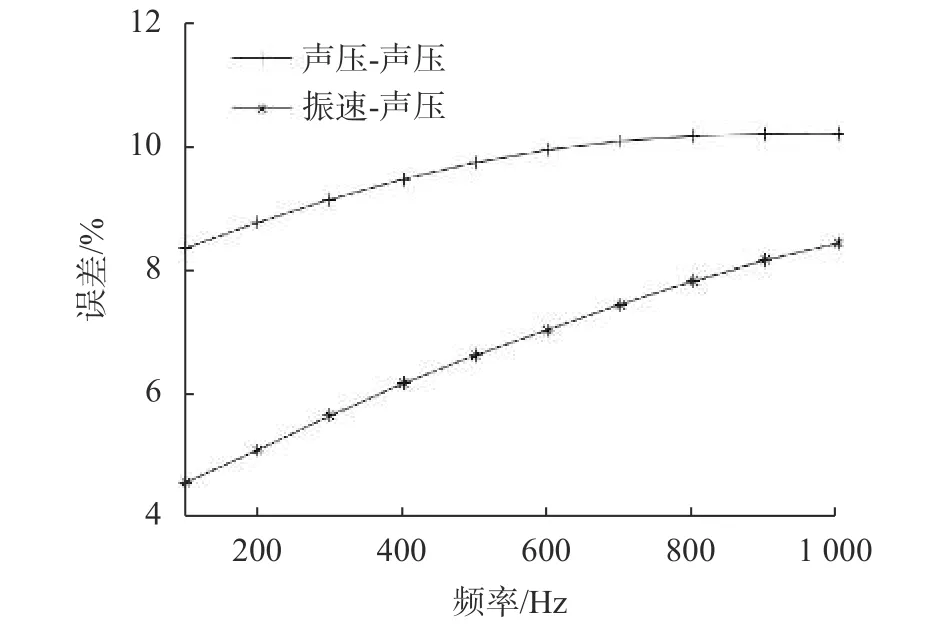
图1 重构误差随声源频率变化曲线图

分析上图变化趋势可以看出，随着声源频率增加，算法的重构误差也在增大，由于近场范围与声源频率有关，近场范围定义为 2D2/λ，D表示声场测量范围长度，λ表示声波波长，频率越高，近场距离越短，因此当在同一距离下测量声场时，频率高的声场复声压相对混叠偏高，声场重构与声源分辨能力较差。另外，通过振速重构声压能更好地对声源定位进行分辨，因此具有更高的重构精度。

2.2 重构距离对两种算法重构精度的影响

修改仿真中声场全息面的采集距离，声源发出500 Hz稳定频率声波，柱体参数不变，重构柱面半径r0=0.15 m，全息测量柱面半径为0.26 m到0.53 m，对算法的重构精度进行计算，重构误差随重构距离变化趋势如图2所示，“+”表示用声压重构声压算法，“*”表示用振速重构声压算法。

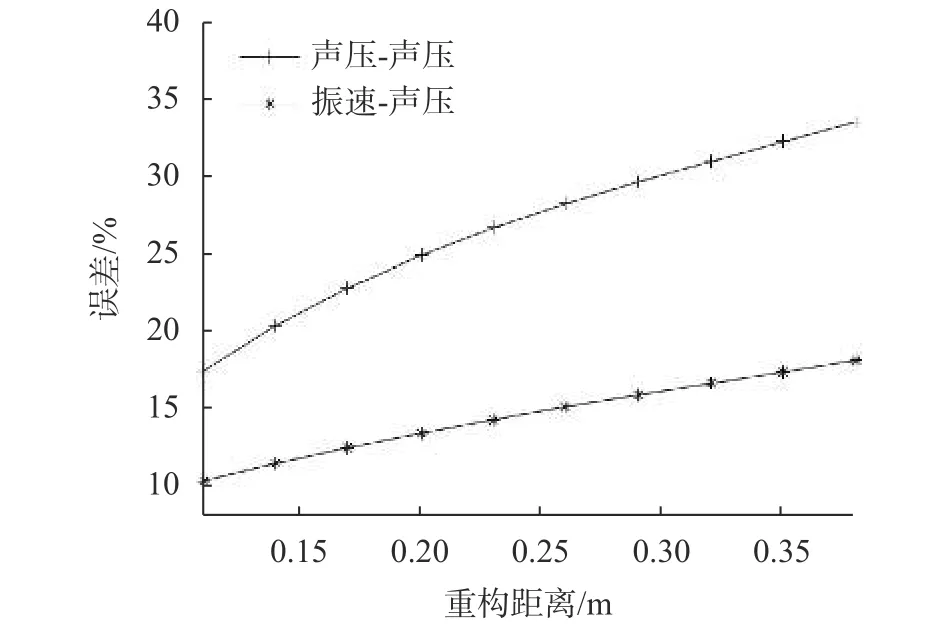
图2 重构误差随重构距离变化曲线图

分析上图曲线看出，随着重构距离增加，声场信号混叠情况严重，算法的重构误差逐渐增大。振速信号的抗干扰性优势更为明显，因此通过振速进行声场重构的计算误差更小，且受重构距离增加的影响更弱，重构误差上升趋势更缓。

3 实验与结果

为验证上文中柱面近场声全息算法的可靠性以及仿真中重构精度的变化规律，在消声水池中进行近场声全息实验。实验中柱体采用φ0.2 m×0.5 m×0.003 m单层加肋碳钢材质，在桶内壁放置激振器，激振器外接信号源与功率放大器，用以调节激振器发出稳定的信号。激振器连接激励杆紧贴桶内壁，带动柱体发出两个同频同相，向水域辐射的声波。在距离桶面d=rH-r0处布放矢量水听器，由PC端控制运动机构调整水听器在水中的位置，矢量水听器的x通道接收端正对声源发射方向，由上而下进行列向声场采集，数据通过采集系统采集后传向PC端进行保存和后处理。当一列声场数据采集完成后控制固定端的旋转杆，使柱体旋转一定角度后进行声场采集。重复上述步骤，即可完成16×21的柱面声场矢量及标量信号测量。相关器材及型号：信号源（RIGOL DG4062）、功率放大器（YE5873A POWER AMPLIFIER）、激振器（SA-JZ002）、矢量水听器、信号调理器（UTC3124）、采集卡、上位机。信号采集系统示意图如图3所示。

将采集得到的声场用本文中的近场声全息方法进行声场重构，并分别计算不同实验工况下的重构精度。

3.1 不同声源频率时的重构情况

当声源频率分别为100 Hz、500 Hz、1 000 Hz时，分别采集距柱体中心r0=0.25 m与r1=0.30 m时的声压与振速声场信号，此时重构距离为0.05 m，对比两种重构方式的声场计算效果，对比结果如图4所示，重构误差如表1所示。

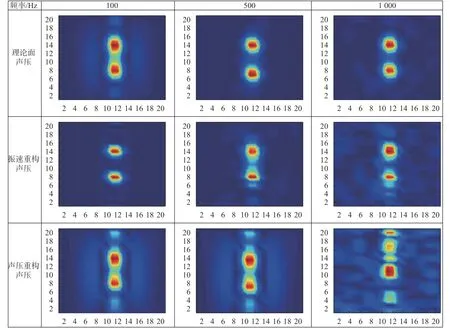
图4 不同声源频率时的声场重构情况

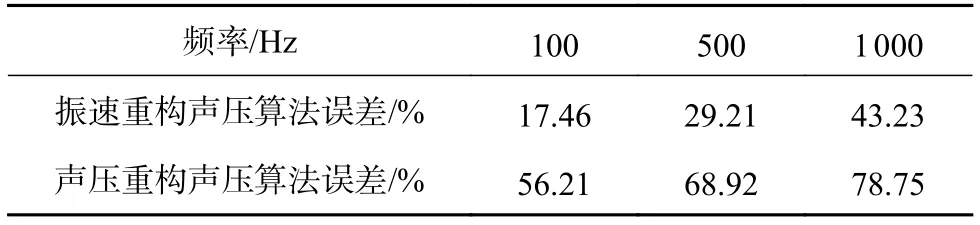
表1 不同频率下的重构误差

由图4及表1重构声场对比效果可以看出，随着声源频率增大，两种算法的重构效果变差，且产生了不同程度的虚像和旁瓣，算法重构误差减小了35%～40%。当声源频率过高时，通过声压进行重构的声场无法对双声源进行较好的区分，因此由振速进行声场重构效果总体优于声压重构算法，且具有较好的声源定位能力。

3.2 不同重构距离时的重构情况

将声源频率设置为500 Hz，分别采集距柱体中心r0=0.25 m与r1=0.30 m、r2=0.35 m、r3=0.40 m时的声压与振速声场信号，此时重构距离分别为0.05 m、0.10 m、0.15 m，两种重构方式的声场计算结果如图5所示，重构误差如表2所示。

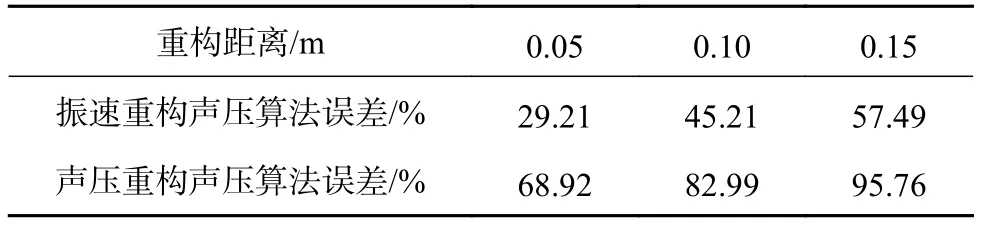
表2 不同重构距离下的重构误差

由图5及表2重构的声场对比效果可以看出，随着重构距离增大，算法的重构效果变差，逐渐产生了旁瓣，此时算法重构误差减小了37%～40%。当重构距离过大时，由声压信号重构的声场已无法进行声源定位，而采集到的振速信号为矢量信号，能对声源所在位置进行还原，因此在距离增大时仍保持较好的声源定位效果。

4 结束语

本文分别用声压和振速信号进行基于统计最优近场声全息的声压重构，从声源频率和重构距离两方面进行算法效果对比。通过仿真和实验发现：用振速进行声场重构时在信号采集中会过滤采集方向以外的信号，因此能够有效屏蔽声场混叠与反射带来的误差，有更好的声源定位能力。随着声源频率增加，重构距离增大，两种近场声全息算法的重构精度都会降低，因此在使用这两种算法进行声场重构时需要注意选取合适的工况。