基于改进ICP算法的波磨区域动态检测方法研究

董庆仑， 尧辉明， 翟字波

(上海工程技术大学，上海 201620)

0 引 言

钢轨波浪形磨耗（波磨）是在钢轨投入使用后轨顶表面沿纵向产生的规律性波浪形不平顺现象。它不仅会缩减轨道使用年限，严重的还会威胁轨道车辆的安全运营[1-5]。所以，准确且全面的波磨检测对制定钢轨维保计划是非常必要的。

常见的波磨检测从检测形式上可以分为静态检测与动态检测，静态检测精度高，但是效率低，且消耗大量的人力资源，所以动态检测是目前常用的波磨检测形式。动态检测在检测原理上分为惯性基准法与弦测法。由于列车低速时加速度信号微弱，容易造成积分饱和，故惯性基准法在低速下误差较大。对此，程朝阳[6]结合惯性基准法传递函数，通过设计低频信号的补偿滤波器解决了数据处理过程中速度移变问题；刘力[7]等联合EMD与小波阈值去噪方法对加速度信号降噪，再通过高通滤波器对积分结果滤波，可以有效反应钢轨波磨值。弦测法根据测量点数的不同可以分为两点弦、三点弦等，测量结果虽不受车速的影响，但如何保证弦测值与波磨值之间传递函数不为0是提高检测精度的关键。魏珲[8]等根据不同波长弦测法复原特性，提出一种结合两点弦与三点弦的广域测量方法，实现不同波长段的波磨复原；王源[9]等根据弦测法原理建立数学模型，提出一种波磨精确值的迭代算法并通过数值仿真验证了其传递函数的优越性；毛晓君[10]等通过推导四点弦测传递函数，将测量结果精度提高到微米级。随着机器视觉技术的发展，利用结构光等光学技术结合弦测法测量波磨的形式也逐渐得到应用，杨杰[11]等利用弦测法提取波磨的波长与波深数据，结合密度聚类算法将三维结构光遍历所得的波磨接触斑进行区分计算，虽然检测效率高于波磨仪，但没有做到真正意义上的动态检测；为了使弦测点始终保持在轨面中心线±10 mm[12]范围内，陈亮[13]运用图像处理算法获得波磨测量点位置，通过动态位置修正保证测量点在有效测量范围，但运用两台机器视觉设备大大增加了检测成本。由此，本文提出一种基于点对加权的改进迭代最近点（iterative closest point, ICP）算法实现精确的点云钢轨轮廓曲线配准，结合弦测法波磨动态检测的优势与结构光面扫描形式，实现了轨顶中心范围内波磨曲面区域的数据提取。

1 动态波磨检测系统方案设计

点线结合动态波磨检测系统主要由两个点激光传感器、一个轮廓线激光传感器、测量运动载体和数据采集系统等组成。系统测量模型如图1所示，前后两个激光测量点与结构光中点三点组成中点弦波磨测量模型，由弦测法可得结构光中点O波磨信息。选取钢轨断面轮廓外侧（未被磨损一侧）数据集及轮廓线上O点弦测波磨真实值为参考点，运用ICP算法将测量轮廓线对齐到标准轮廓线，求得轨顶波磨曲面信息。

图1 系统测量模型示意图

2 点线结合动态波磨检测算法

2.1 结构光视觉模型及系统标定

结构光视觉测量的数学建模过程如图2所示，其中Owxwywzw为大地坐标系，Ocxcyczc为相机坐标系，Ouuv为像素坐标系，将成像平面与相机光轴zc交点O1作为图像平面坐标系O1xuyu的坐标原点。

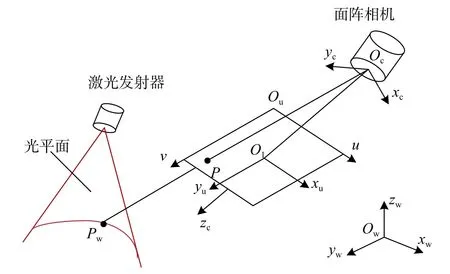
图2 结构光视觉测量数学模型

假设P为空间中一点，其在各个坐标系下的齐次坐标矩阵分别为Pw=(xw,yw,zw,1)T，Pc=(xc,yc,zc,1)T，P=(u,v,1)T，根据相机成像模型有：

式中：ρ——比例因子；

A——相机的内部参数矩阵。

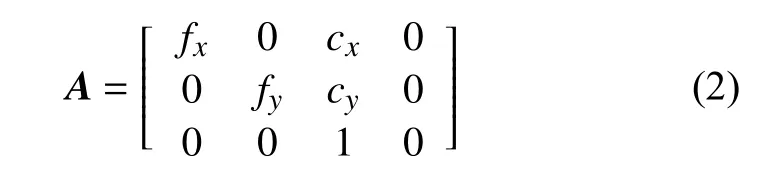
式中：(cx,cy)——相机的主点坐标；

fx,fy——相机的有效焦距。

相机的外部参数矩阵M：

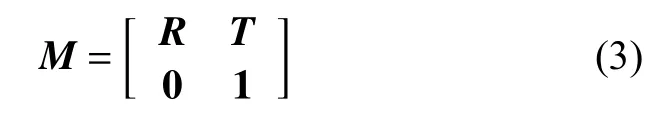
式中：R——大地坐标系向相机坐标系转换的旋转矩阵；

T——平移矩阵。

光平面在空间坐标系下的空间方程为：

式中：a,b,c,d为光平面方程系数。

直线Ocp的方程可由式（1）确定，联立式（4），即为结构光视觉测量的数学模型：

经对相机内部参数标定[14]与结构光平面标定[15]后，由式（5）确定的结构光视觉测量模型可以计算出结构光条上任一点的世界坐标。

2.2 结构光中点真实值获取

车辆载体在运动过程中，会产生由于轨道长期使用导致多几何方向不平顺所引起的左右颠簸蛇形运动现象，从而导致结构光中点不能总是与轨顶中心线重合，即随着车体的运动，每个瞬时结构光中点位置相对于钢轨横向与垂向都是变化的。对此，针对每条采样点云轮廓线中点，利用三点弦测法计算其垂向位置变化，利用结构光在钢轨表面的跳变值计算其横向位置变化。

2.2.1 结构光中点垂向位置计算

钢轨波磨测量的弦测法是一种常用的动态波磨测量方式，以首尾两端的连线作为弦，以中间弦测点到弦的距离作为波磨测量值，本检测系统设计中点弦测法3个测量点由前后两个激光点与结构光中点组成，其测量原理如图3所示。

图3 中点弦测法原理示意图

轨道实际不平顺f(x)与弦测值y(x)关系为

转换到频域为

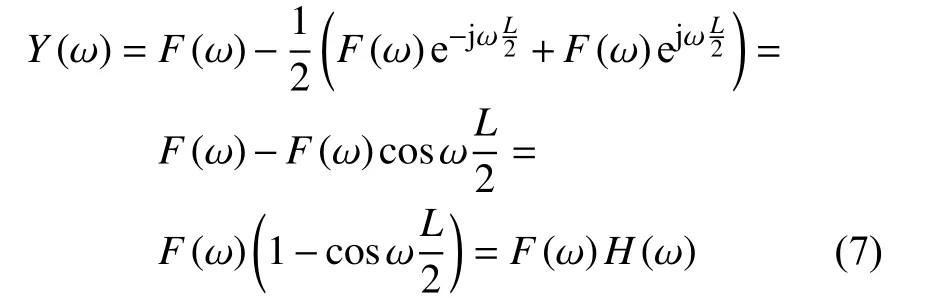
式中：α——常数；

[ω1,ω2]——复原的空间频率区间范围；

Hi(ω)——逆滤波器频率响应函数。

三点弦测法可以有效去除动态检测由车体振动引起的纵向颠簸误差，进而还原结构光中点的垂向高度信息。

2.2.2 结构光中点横向位置计算

由于测量系统载体的蛇形运动，结构光中点不总在轨顶中心线上即其在点云轮廓线上的横向位置是不固定的。以轨道纵向为y轴方向，轨道横向为x轴方向，波磨高度信息为z轴方向，在测量过程中，轮廓传感器的点云密度会随着车体在z轴方向的不规则运动而改变。设测量原点的轮廓点云密度为ρ，轮廓的有效宽度（两跳变值之间距离）为b，有效轮廓点云个数为N，原点高度数据为Z则有

由相似三角形定理得第i个采样轮廓的点云密度，如下式所示。

第i个采样时刻结构光中点相对于轨顶中点偏移量：

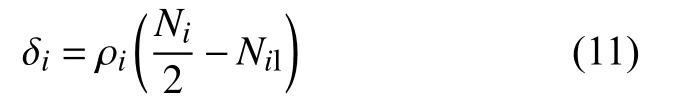
其中Nil为第i个采样时刻结构光中点与左跳变点之间点云数据个数。

2.3 点云轮廓曲线配准

钢轨波磨主要出现在轨顶中心线±10 mm区域内，只要获得准确的轨头断面轮廓曲线，使之与轮廓标准曲线点云配准，便可精确获得轨顶表面的波磨信息。选取轨顶外侧数据为基准，结合结构光中点真实位置信息，利用点对加权的改进ICP算法将轨头测量轮廓对齐到轨头标准轮廓，求得波磨值。

2.3.1 ICP算法

ICP算法，是一种基于最小二乘法的点云精确配准算法，通过重复进行选择对应关系点对，计算最优刚体变化矩阵，直到满足设定的阈值要求。假设源点云为P，目标点云为Q，对于P中每一个点Pi，在Q中查找与其最近的点Qi作为其对应点，则所有点对构成的误差函数式为

式中：Ro,to——点云配准的旋转矩阵与平移向量；

No——点对数量。

求解使f(Ro,to)最小的Ro,to，并记录此时最小误差ek，将前一次计算出的Ro,to应用于P，即得到第二次迭代的初始点云P′：

重复上述步骤直至接连两次迭代的误差函数值变化量 |ek-ek-1|小于提前设定的阈值。

2.3.2 点对加权的轮廓曲线配准

如图4为设计坐标系下的标准钢轨断面轮廓，CE段为钢轨头部未被磨损的一侧，AB段为轨顶波磨检测的有效区域，点D为弦测法理想轨顶中心线测量点，在本文中为轮廓传感器结构光中点，其实际位置随机出现在AB之间。传统ICP算法构造误差函数时对所有点对等权叠加，但在实际情况下对每对点对的迭代精度要求是不同的。如只以CE段点云作为点云配准初始点集容易出现如图5所示局部最优解，本文中，以CE段点云与结构光中点D构造从测量坐标系到设计坐标系基于ICP算法的点云配准，构造误差函数时，对在波磨有效测量区域内的D点及对应点点对的精度要求要高于CE段点云点对，所以有：

图4 标准钢轨断面轮廓图

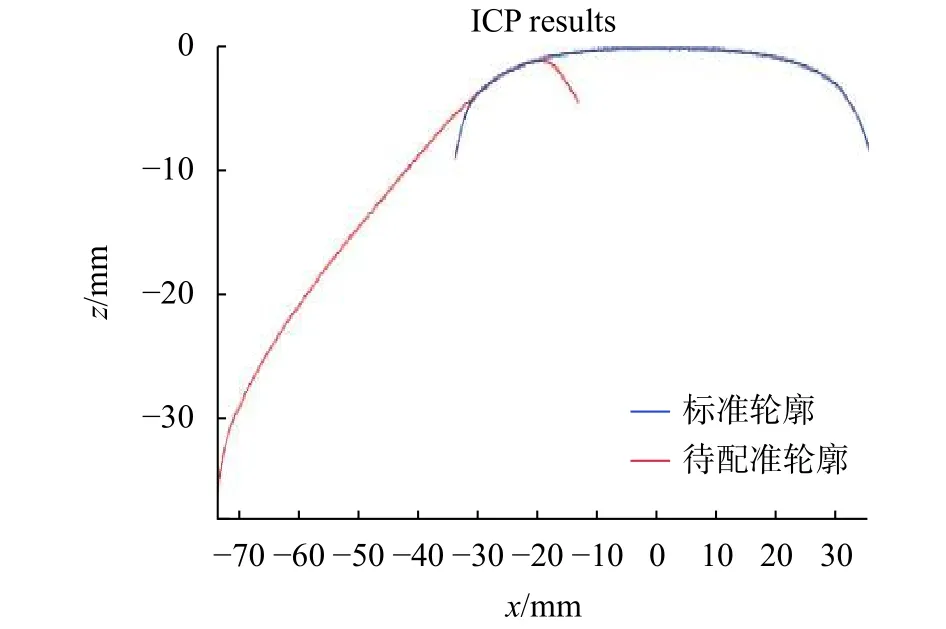
图5 局部最优案例图

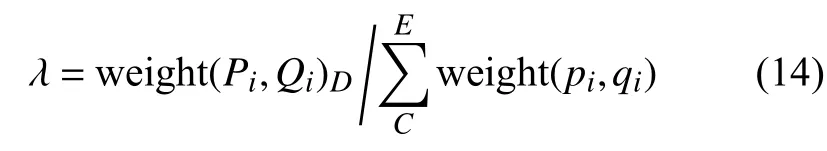
其中 λ为D点及其对应点点对权重与AC段所有点对权重之和的比值。

对动态工况下测得同一轮廓分别运用传统ICP算法和点对加权的改进ICP算法进行轮廓点云配准的多次比较，前者的配准速度约为后者的1.24倍，图6与图7分别为某次采样点完成钢轨轮廓配准两种算法的迭代次数；以静态测量的轮廓点云为基准，后者的配准精度提高了56%。

图6 传统ICP算法迭代次数

图7 改进ICP算法迭代次数

为了使式（11）与式（13）确定的目标函数取得最优，首先要完成迭代初值的选取，以确保迭代的收敛性，其次是确定最近点搜索方式，以减少基准对其的时间。挂载轮廓激光传感器的检测装置载体在运行过程中与钢轨的相对位置比较稳定，点云轮廓线在图像中的位置变化不大。

3 实验设备

为完成对点线结合式动态曲面检测算法的验证，设计以CAT型波磨检测车为基础的实验装置如图8所示，其具有的功能及特点如下：满足动态三点弦测法的实验要求；满足点线结合式钢轨动态波磨采集数据；弦测点位置可调节。实验将传统三点弦测法中间波磨测量1D激光点改为更为先进的2D激光传感器轮廓线，是一种新型的波磨测量方式。

图8 实验装置结构图

选用前后两激光传感器与中间轮廓激光传感器双线程的数据采集模式，避免因数据量过大引起的数据丢失，两个激光传感器数据采集由MCU微处理器控制，数据经无线传输至上位机，轮廓激光传感器采集数据由I/O线缆直接传至上位机。为实现三独立传感器的数据同步，采用TRD-MX型编码器同步发送采集脉冲，使传感器的采样由时间域转变为空间域，提高了信息的定位精度。

4 数据处理与分析

在实验室条件下，对一段0.85 m钢轨表面进行多次动态检测实验，本实验采用中点弦测法，将2D轮廓激光传感器置于左右两1D激光传感器中间位置，弦长为1 m，载体移动速度为5 km/h，λ取0.1。数据处理算法流程如图9所示，以左右两点与中间线中点为弦测法三测量点，经逆滤波算法得结构光中点真实波磨值，并结合轨顶外侧未被磨损段为ICP点云配准算法基准数据集。

图9 数据处理算法流程图

将校准后的实验装置与传感器置于轨道未被磨损的位置所采集的轮廓线作为算法轮廓基准，图10为某位置处基准轮廓与待配准轮廓相对位置，以弦测法所得结构光中点波磨真实值与轨道未被磨损一侧点云数据为基准，利用点对加权的改进ICP算法配准后的轮廓相对位置如图11所示，所得其中点±10 mm范围内波磨值如图12所示。

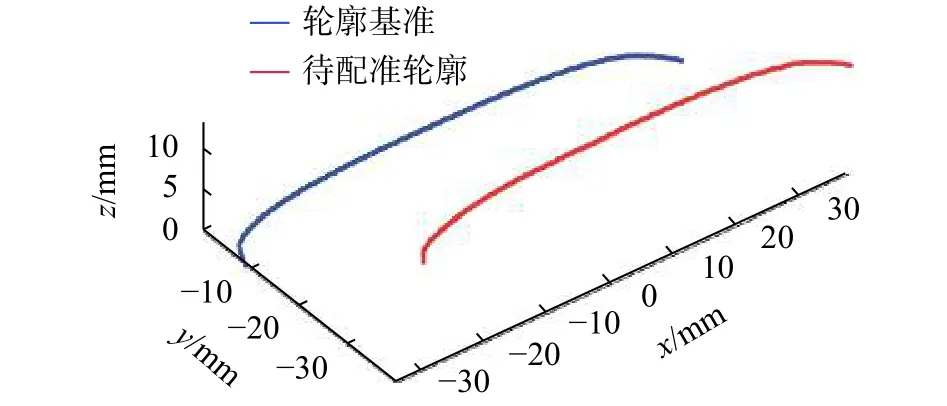
图10 基准轮廓与待配准轮廓相对位置

图11 配准后轮廓相对位置

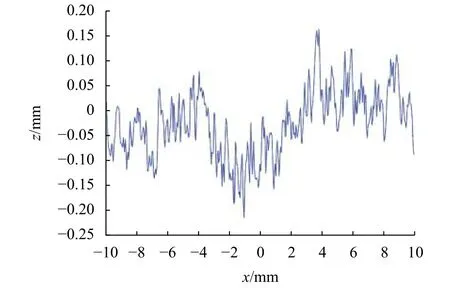
图12 算法处理后轮廓中点±10mm波磨值

连续对同一截面测量10次，记录每次轮廓中点±10 mm范围内波峰与波谷值，表1为固定位置轮廓每次测量结果，以标准差评价测量重复性精度，Vmax为0.049 mm，Vmin为0.045 mm。

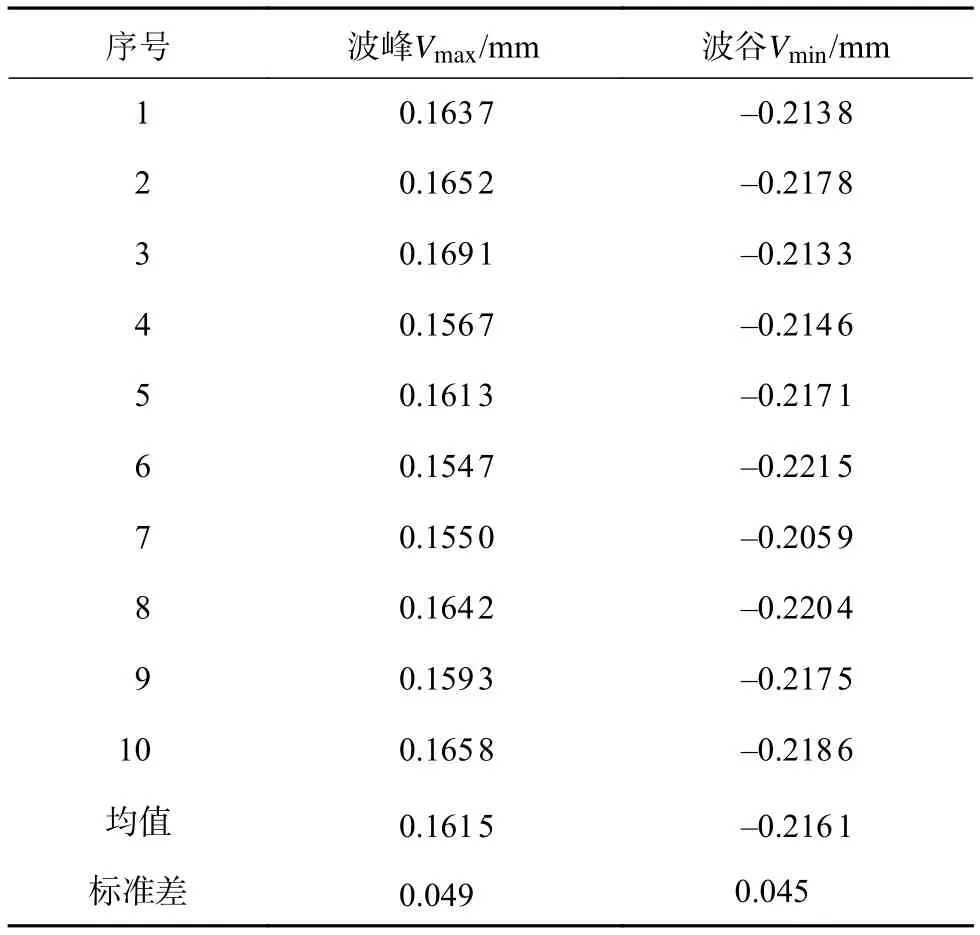
表1 单轮廓波磨测量结果

将每个采样点对应轮廓配准到标准轮廓，如图13所示，为部分轮廓配准后钢轨表面三维效果图。

图13 部分轮廓配准后钢轨表面效果图

5 结束语

本文以点线结合的波磨测量方式，结合点云轮廓数据与传统动态波磨检测弦测法获得结构光中点真实波磨值，使其与钢轨轨头未被磨损一侧共同作为点云配准参考点集，利用点对加权的ICP点云精确配准算法将测量轮廓配准到标准轮廓，获得轨顶中心线±10 mm范围内波磨曲面信息。该方法将传统弦测法波磨测量与结构光点云配准技术相结合，实现了从二维的波磨曲线提取到三维波磨曲面的提取，经多次重复性实验证明本文波磨测量方式的最大标准差为0.049 mm，具有良好的测量精度。