中小直径棒料径向掰断低应力下料起裂机理研究

徐嘉怡，张立军，孙旭东，周强，杨宁

(中国石油大学(华东) 机电工程学院，山东青岛，266580)

下料是机械制造中金属成型的第一道工序，由于传统的下料方式如剪切、锯切等存在材料浪费严重、能耗大、环境污染严重等问题[1]，一种基于裂纹技术的低应力下料方法应运而生，这种下料方式具有材料利用率高、加载力小等优点，符合绿色制造的要求[2]。一些学者对不同的低应力下料加载方式进行了研究。景飞等[3]提出旋转疲劳弯曲的精密下料加载方式并对旋转疲劳弯曲加载机理进行了分析；张立军等[4-6]研究了液压补偿型低应力精密断料和高速离心下料中的棒料断裂机理，提出了单臂低应力下料合适的工艺参数；ZHANG等[7]研究了变频振动精密下料方法的工艺参数，通过改变振动频率提高断面质量；TANG 等[8]提出旋转冲击精密下料方式，设计了旋转冲击精密下料机；WANG 等[9-10]提出了通过液压补偿和调节力臂实现控制加载力的低应力下料系统。目前的低应力下料方式大多为单臂加载的周向加压下料，由于夹持端反支力的影响，棒料V 型槽尖端同时受到拉应力和切应力共同作用，导致萌生的裂纹为复合裂纹，难以对起裂过程进行有效控制，而初始裂纹的起裂方向又直接影响下料效果，起裂不可控导致下料效率低，断面质量不理想。因此，低应力下料没有被规模化应用，为了尽早实现低应力下料的工业化，本文作者提出径向掰断低应力下料法，借助ABAQUS 软件进行有限元仿真分析，应用正交试验法对仿真结果进行研究，获取提高棒料低应力下料质量和效率的工艺参数。

1 径向掰断低应力下料机理

低应力下料是一种利用裂纹技术，通过人为控制裂纹的萌生和扩展，达到材料分离目的的下料方式。目前的低应力下料技术是首先给棒料表面预制V 型槽，再对棒料施加一定的外载荷，进行低周疲劳加载，使V 型槽尖端处产生应力集中效应，出现裂纹并扩展[7]。通过控制载荷和加载位置等外部条件，最后实现棒料完全断裂。因此裂纹的起裂位置、起裂方向等参数直接影响棒料的断面质量[6]。

径向掰断低应力下料工作原理如图1所示。径向掰断低应力下料原理是在棒料V 型槽两侧对称同步加载，加载力F与夹持力在V型槽两侧对称分布。夹持力臂L1与加载力臂L2以V 型槽尖端为对称轴线在两节棒料上对称，这能减小V 型槽尖端应力场中的切应力，使单臂加载的复合型裂纹转化成I型裂纹，实现裂纹萌生于V型槽尖端，并减小起裂角。图1中棒料下方对称设置的推力锤头和棒料上方对称施加的加载力为一个施力组合，在棒料圆周上设置4～8组力组合依次加载，对棒料进行圆周变加压加载以使裂纹周向均匀扩展。

图1 径向掰断低应力下料工作原理图Fig.1 Working principle diagram of radial breaking of low-stress cropping

2 径向掰断下料起裂原理分析

根据径向掰断的力学模型，理想状态下棒料为纯弯曲变形，其V 型槽尖端的横截面上只有弯矩，裂纹应为纯I 型[11]。根据断裂力学对裂纹尖端应力集中的研究理论，带有预制V 型槽的构件受到外载荷的作用，在V 型槽底部应力增大产生初始裂纹[12]。I 型裂纹的应力强度因子KI决定了裂纹尖端具有奇异性的应力场的强度，当KI达到I型裂纹的材料断裂韧性KIC时，棒料的初始微裂纹发生失稳扩展。根据最大周向正应力理论的基本方程[13]：

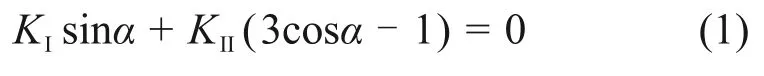
其中：α为起裂角；KI为I型裂纹的应力强度因子；KII为II型裂纹的应力强度因子，对于纯I型裂纹，KII=0，得：

此时裂纹应沿V 型槽底部向所在横截面的中心扩展，起裂角应为0°。但在实际下料过程中往往存在一定的起裂角，即产生的裂纹为复合裂纹，这是因为裂纹方位、载荷分布不能够完全对称或材料不能达到严格的各向同性等。研究裂纹的起裂质量和起裂条件对径向掰断低应力下料的工业化应用十分关键，而下料过程中的复合型裂纹的起裂质量和起裂条件通过理论分析很难得到准确结果，本文通过仿真技术与理论分析相结合的方法对径向掰断低应力下料的起裂阶段进行探究。

3 棒料V型槽尖端起裂仿真研究

3.1 有限元三维模型的建立

采用文献[6]提出的棒料低应力下料有限元分析模型和加载方式，以棒料直径d=15 mm 为例进行研究。棒料毛坯通常需要加工45°的倒角[14]，为减少后续加工，选择V型槽张角φ=90°，单节棒料长度L=40 mm。利用ABAQUS 软件中的part 模块建立棒料有限元分析模型，如图2所示。为提高计算精度与可靠性，将棒料分为左右棒体、V型槽底部及两侧过渡边5个部分，进行2种类型的网格划分，其中左右棒体及V 型槽底部采用六面体C3D8R 网格划分，棒体网格最小边长为1 mm，V 型槽底部进行最小边长为0.2 mm 的网格细化；而两侧过渡边采用四面体二次单元C3D10 进行网格划分，共划分84 651个结点，52 112个网格。棒料材料为45 号钢，性能参数如表1 所示，在ABAQUS 中采用XFEM 仿真分析[15]，边界条件和加载方式为以V 型槽为中心，两侧对称，在棒料下方夹持力处各添加3个平动自由度的约束，棒料上方加载力处各添加竖直向下的集中静态加载力，模拟径向掰断加载方式。为探究径向掰断下料的最佳工艺参数，采用正交试验法探讨夹持力臂L1、加载力臂L2、V 型槽槽深q和底角半径ρ对起裂偏距e和起裂角α的影响规律。

图2 棒料有限元三维模型Fig.2 Finite element 3D model of bar

表1 棒材性能参数Table 1 Material performance parameters

3.2 正交试验方案

正交试验是一种使试验次数尽可能减少且所得结果与全面试验所得的结果相差不大的统计方法。本文通过“正交表”用尽可能少的仿真试验获得典型数据，分析掰断下料的最佳工艺参数[16]。根据掰断棒料的下料原理，取夹持力臂L1(因素A)，加载力臂L2(因素B)，槽深q(因素C)和底角半径ρ(因素D)4 个因素，每个因素根据实际的加工范围选取5 个水平，选用L25(54)正交表，正交试验方案及仿真实验结果如表2所示。

表2 试验方案及仿真结果Table 2 Test scheme and simulation results

仿真实验结果以起裂偏距e和起裂角α为评价指标，同时作为每次试验的评价参数得分，e和α含义如图3所示，其中，起裂偏距e定义为起裂点位置与V型槽最底部的水平最短距离，起裂角α定义为裂纹的径向起裂角。

图3 起裂偏距和起裂角的定义Fig.3 Definition of crack initiation deviation and initiation angle

3.3 仿真结果分析

该正交试验有起裂偏距和起裂角2个指标，采用多指标正交试验分析方法中的综合平衡法进行分析[16]，即先对各指标分别按单一指标进行直观分析，然后再对各指标的分析结果进行综合比较，得出最佳试验方案。表3所示为以起裂偏距和起裂角为评价指标，通过极差分析得到较优水平和因子主次。最优方案使起裂偏距和起裂角尽可能小，结果分析时得分越小，试验所得效果越好。K表示单一因子各水平的分数；极差为各因素主效应的差值，表示该因素的重要水平，因子主次根据对应的极差排序，表示对试验结果的影响程度。通过分析以起裂偏距为评价指标的K和以起裂角为评价指标的K，得到单一指标的较优水平组合，再通过综合平衡法给出起裂偏距和起裂角的较优水平组合，得到试验的最优方案。

表3 试验结果分析Table 3 Analysis of test results

3.3.1 起裂偏距下较优水平的确定

起裂偏距e对断面质量和下料效率有直接影响。在理想下料过程中，裂纹在V型槽尖端萌生，即起裂偏距为0，但在实际下料过程中，由于棒料加工工艺和加载方式很难达到理想状态，最大主应力常出现在偏离V 型槽尖端处，即出现起裂偏距，进而影响裂纹的扩展走向，因此，在下料过程中应尽量减小起裂偏距。初始裂纹在V 型槽底端最大主应力处萌生，如图4所示，掰断下料棒料起裂前一个时刻的应力云图中，Mises应力和最大主应力集中在V型槽底部，τxy切应力关于V型槽底部近似呈对称分布。

图4 径向掰断低应力下料V型槽尖端的应力云图Fig.4 Stress contour of V-shaped notch tip with radial breaking of low-stress cropping

根据表3中起裂偏距极差可知，对起裂偏距影响最大的因素是底角半径，影响最小的是加载力臂。因为径向掰断的加载方式为关于棒料V 型槽最底部对称施加加载力，起裂偏距在V 型槽底部对称的两侧随机起裂，而在工业化可实现的范围内，底角半径越小，应力集中效果越好，起裂位置越靠近V 型槽最底部，起裂偏距就越小[4]，因此，对于起裂偏距评价指标的较优水平的组合是

3.3.2 起裂角下较优水平的确定

棒料V 型槽底部应力场复杂，形成了立体的不规则裂纹，如图5所示。起裂角总体分为从棒料表面向内部扩展的径向起裂角α和沿棒料表面圆周扩展的周向起裂角β(见图3)，2种起裂角均对棒料断面质量均产生直接影响，即起裂角越小，起始断面越平整。由于径向掰断下料方式在V 型槽尖端基本消除了切应力，周向起裂角β极小可以忽略不计，因此本文中未特别说明的起裂角是指径向起裂角α。根据表3 中起裂角极差，对起裂角偏距影响最大的因素是底角半径，影响最小的是夹持力臂。起裂角主要与V 型槽底端的切应力相关，而切应力在V型槽底部近似呈对称分布，如图4所示。底角半径影响V 型槽底部的应力集中程度，底角半径减小使得主应力与切应力的比值增大，萌生的裂纹也能更好地向棒料中心径向扩展，从而减小起裂角。以起裂角为评价指标的较优水平组合是A1B1C1D1。

图5 径向掰断低应力下料初始裂纹形态Fig.5 Initial crack morphology of radial breaking of lowstress cropping

3.3.3 较优工艺参数分析

根据综合平衡法综合考虑2个评价指标，对起裂偏距和起裂角影响最大的都是底角半径，较优水平均为D1，由于现用开槽工艺开槽越深对刀具的磨损越大，能耗也越高，且开槽过程中产生一定的材料浪费，因此，在影响断面质量较小的情况下选择槽深较小的水平C1；夹持力臂和加载力臂对起裂偏距和起裂角的影响较小，根据径向掰断力学原理，同侧夹持力与加载力的距离越远，棒料所受弯矩越大，因此，选择较小的夹持力臂和较大的加载力臂A1B5。综合以上因素可知，较优的工艺参数如下：夹持力臂为5 mm，加载力臂为35 mm，槽深为0.6 mm，底角半径为0.1 mm。

4 径向掰断下料效果优势分析

4.1 对起裂质量的影响

对于不同的加载方式，V 型槽处的应力状态不同。图6所示为目前常见的棒料单臂加载低应力下料原理图，在棒料V 型槽一端使用夹持机构对棒料进行固定，另一端进行周向加载。图7所示为仿真中单臂加载低应力下料方式起裂前一时刻棒料V型槽尖端的应力状态。由图7可知，棒料V型槽处的最大主应力分布不对称，而是偏向V 型槽底部附近靠近加载力一侧，这就导致裂纹萌生位置出现在靠近加载力一侧，Mises应力和切应力集中在V型槽底部靠右侧，萌生的裂纹扩展时偏离垂直于棒料中心的方向，使断面凹凸不平[6]。这主要与单臂加载时棒料V型槽处的受力状态有关。

图6 单臂加载低应力下料原理图Fig.6 Schematic diagram of single-arm loading lowstress cropping

图7 单臂加载低应力下料V型槽尖端的应力云图Fig.7 Stress contour of V-shaped notch tip of single-arm loading low-stress cropping

单臂加载方式的最佳加载参数为L1=15 mm，L2=30 mm[6]。单臂加载低应力下料初始裂纹形态如图8所示。单臂加载方式中应力分布的不对称也导致了径向起裂角增大且同时出现周向起裂角，切应力导致V型槽处的应力集中效应减小。

图8 单臂加载低应力下料初始裂纹形态Fig.8 Initial crack morphology of single-arm loading low-stress cropping

图9所示为在最佳加载参数下掰断加载和单臂加载2 种方式V 型槽处的应力最大值对比。从图9可以看出，掰断下料方式的最大应力关于V 型槽中心对称分布，而单臂下料应力最大值分布复杂，导致起裂质量相对较差。与单臂加载最佳加载参数的起裂评价指标相比，基于较优工艺参数进行径向掰断加载得到的起裂偏距减小了8.2%，径向起裂角减小了17.9%。进一步试验结果显示，此较优工艺参数对直径为12～20 mm、单节大于35 mm的常用长度45 号钢棒料进行径向掰断低应力下料同样适用。

图9 棒料表面最大主应力对比Fig.9 Comparison of the maximum principal stress on surface of bars

4.2 临界起裂加载力的估算

4.2.1 确定临界起裂加载力的意义

在棒料参数确定的情况下，通常V 型槽尖端的临界起裂力是一定的，对于不同的加载方式和加载参数，只要得到棒料起裂所需的临界起裂加载力，令实际加载力大于临界起裂加载力，即可实现棒料的起裂加载[17]。下料过程中施加准确的临界起裂加载力能够缩短起裂时间，进而提高下料效率。对于目前单臂加载的下料方式，棒料V 型槽尖端起裂加载力是根据断裂力学的估算和有限的经验数据得出的，由于这种加载方式下V 型槽尖端应力场复杂，理论计算较为困难，数值模拟得出的数据规律性较弱，因此，很难采用理论分析和数值模拟的方法来准确计算下料时棒料V 型槽起裂力，进而难以对起裂力进行有效估算，导致起裂过程不易可靠控制：起裂加载力过小，导致起裂时间增加或下料不成功；起裂加载力过大，棒料瞬断区面积增大导致下料断面质量变差，从而使得断面质量与下料时间无法同时达到最优解，限制了这种低应力下料方法的工业化应用[18]。但是对于径向掰断的低应力下料加载方式，因其棒料V型槽处应力场分布对称，主应力集中，力学模型相对容易建立，理论分析数值偏差较小，对仿真结果进行拟合的准确性也高，因此可以通过理论分析和仿真相结合的方式计算起裂加载力。

4.2.2 临界起裂加载力的确定方法

临界起裂加载力的确定方法和步骤如图10 所示。在ABAQUS 中进行仿真试验的流程为：首先细化分析步跨度，保证裂纹萌生时的起裂力为棒料起裂的临界加载力，进而能够控制棒料的起裂深度满足初始裂纹要求，即起裂深度为0.1～0.2 mm[10](图5)。然后，根据裂纹萌生时的分析步时间和施加总载荷计算临界加载力。棒料的强度极限与通过临界加载力计算所得的最大正应力比值即为V型槽尖端的应力集中系数[19]。进行多组棒料参数和加载参数的仿真试验并得到对应的临界加载力后，运用MATLAB 进行数据拟合得到应力集中系数的表达式。最后，通过仿真试验对应力集中系数表达式进行准确性验证，即可确定不同加载参数的临界起裂加载力。

图10 确定临界起裂加载力公式流程图Fig.10 Flow chart to determine formula of critical crack initiation loading force

4.2.3 临界起裂加载力计算公式

针对径向掰断加载方式的力学模型，V型槽尖端起裂所需的临界起裂加载力计算公式为[20]：

式中：k为应力集中系数；δb为材料的强度极限，MPa；d为棒料直径，mm；q为V型槽深度，mm；d=2a+2q。由式(3)和图1可知，临界起裂加载力与V型槽处截面半径a和实际力臂(L2-L1)有关。本文中以45 号钢为例，参数如表1 所示，根据实际工况固定d和L1进行仿真试验，用MATLAB 进行数据拟合计算，综合考虑拟合效果，得到k关于变量q和L2表达式：

图11 所示为基于仿真实验结果的应力集中系数公式拟合图，用确定系数R2表征仿真试验结果拟合程度，R2为预测数据和原始数据均值之差的平方和与原始数据和均值之差的平方和的比值，确定系数的取值范围为[0，1]。R2越大，表明建立的方程模型对数据拟合效果越好，即q和L2对k的解释能力越强。根据式(4)得出R2=0.848，可见通过式(3)和(4)计算得出的临界起裂加载力与仿真所得结果在取值范围内(V 型槽深度为0.6～1.4 mm，加载力臂为15～35 mm)，高度吻合，因此，通过公式可方便地对不同参数棒料的临界起裂加载力进行估算。

图11 基于仿真结果的应力集中系数公式拟合图Fig.11 Formula fitting diagram of stress concentration factor base on simulation results

5 结论

1)提出了中小直径棒料径向掰断的低应力下料方法，该方法提高了棒料的起裂质量和起裂力估算准确性。

2)建立了中小直径棒料径向掰断下料的仿真模型。通过对直径d=15 mm 棒料进行正交试验，得到针对直径为12～20 mm、单节大于35 mm的45号钢棒料径向掰断加载方式的较优工艺参数组合为L1=5 mm，L2=35 mm，q=0.6 mm，ρ=0.1 mm，得到的相应起裂角为4.24°，起裂偏距为0.009 mm，在V型槽底部中心起裂。

3) 提出了能够满足工业化应用的评判标准：棒料起裂质量起裂角＜5°，起裂偏距＜0.05 mm。基于起裂偏距和起裂角的评价指标，与目前的单臂下料方式相比，径向掰断下料的起裂质量较高，且掰断下料时起裂力范围可以通过理论计算和仿真分析确定，在研究取值范围内准确性较高，方便获得不同参数下棒料径向掰断低应力下料的临界起裂力。