基于尖点突变模型的微波加热固体介质的热失控分析

杨彪，邓卓，刘志邦，母其海，朱娜

(1.昆明理工大学信息工程与自动化学院，云南昆明，650500；2.昆明理工大学云南省人工智能重点实验室，云南昆明，650500；3.昆明理工大学非常规冶金教育部重点实验室，云南昆明，650093)

微波加热作为一种新型的绿色冶金方法，通过微波在介质内部的介电损耗直接将能量选择性地传递给被加热介质的分子或原子，宏观上表现出可选择性加热、加热均匀、热效率高、清洁无污染、启动和停止加热迅速等优越特性。由于微波加热具有独特的优势，美国能源部已将微波加热技术列为一种新能源和振兴现代制造业的技术。在微波加热过程中，随温度升高，会出现“热失控”的宏观现象。“热失控”是微波与物料相互作用形成正反馈的结果，微波输入功率的微小改变会导致被加热物料温度发生剧烈变化[1]。KENKRE等[2]研究了微波加热陶瓷的温度变化过程，并用经验公式对该过程中温度的急剧升高进行描述。KRIEGSMANN[3]建立了微波加热陶瓷板的一维模型，在渐进分析的基础上预测了物料温度与微波输入功率之间的关系，发现当物料电导率与温度呈指数关系时，可描述为“S”形曲线。此后，该预测结果在许多理论研究中得到证明，但并未通过实验方法证实。STUERGA 等[4]在微波加热冷冻物体过程中，分析温升曲线的斜率变化形式，为S形曲线提供了实验依据。随着对热失控现象的深入研究，众多研究者从不同角度对热失控现象进行研究，并在微波加热热失控的控制研究方面取得了显著成果[5-9]。由于热失控发生时物料升温很快，研究者们大多采用定性方法对该过程进行分析，对其定量研究相对较少，且温度的“跳跃式”变化难以用传统的微积分方法进行研究。本文作者将突变理论引入热失控研究，并采用有限元方法进行数值模拟，实现微波加热热失控的定量分析。

突变理论是一门以现代控制理论和拓扑学为基础，通过将突变现象用数学方式描述为7种基本初等突变，以解决非线性系统中不连续跳变问题的方法。其中，尖点突变模型使用最广，具有突然跳跃性、滞后性、双模态、不可达性和发散性等基本特点[10]。在尖点突变模型中，系统的控制变量和状态变量构成系统的平衡曲面，系统在连续变化的控制变量作用下，其状态变量会发生不连续的跳变，在图形上表现为一个带尖点的S 形曲面。尖点突变理论被广泛应用于隧道[11-14]、边坡[15-17]、岩土[18-19]、交通流模型[20-21]等多个领域，并能为其他领域突变现象的研究提供相应的理论基础和研究依据。

本文基于微波加热原理，通过将突变理论与微波加热热失控的产生机理相结合，构造出热失控的尖点突变模型，分析尖点突变模型得到判断加热过程中温度稳定性的充要判据及临界温度表达式，从而实现对热失控现象的定量研究。使用有限元方法，通过COMSOL Multiphysics软件平台模拟微波加热碳化硅陶瓷过程，对尖点突变模型中的稳定性判据进行数值计算，并结合临界温度表达式，从而实现微波加热陶瓷介质热失控的定量分析，进而判断微波加热系统的稳定性。

1 微波加热系统模型

1.1 物料的电磁特性

微波加热过程涉及电磁场、温度场及运动场在内的多物理场耦合、分布参数的非线性问题。其中，电磁场满足Maxwell方程组，其微分形式表示如下：

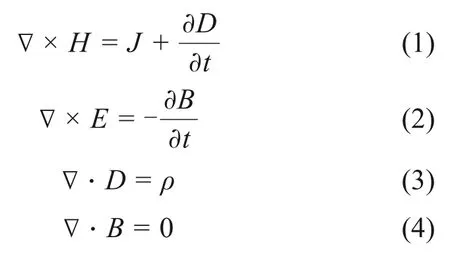
式中：H为磁场强度，A/m；D为电位移，C/m2；E为电场强度，V/m；B为磁通量密度，Wb/m2；J为电流密度，A/m2；ρ为电荷密度，C/m3。H，D，E，B和ρ均为空间位置和时间的函数。

温度场满足的热传导方程表示如下：

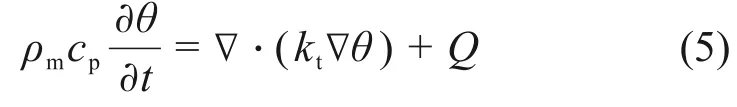
式中：θ为物料温度；ρm和cp分别为物料的密度和比热容；kt为热传导系数；Q为微波加热过程中电磁功率的损耗。

微波加热实质是微波穿透加热物料，物料吸收微波能并将其转化为热能，从而实现快速加热的过程。在此过程中涉及微波能的吸收与转换。对于介质材料，考虑其在微波电磁场中的加热效果与其介电特性密切相关，在电磁场中可用本构关系进行表示。描述电场、磁场及物料介电特性之间关系的本构方程表示如下[22]：

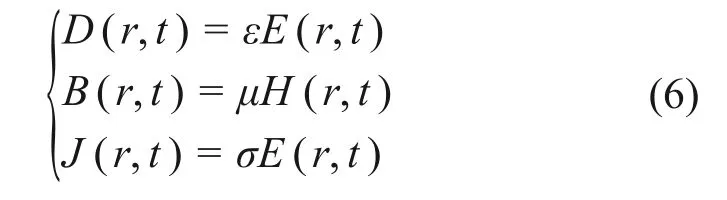
式中：ε，μ和σ分别为介电系数、磁导率和电导率，是影响微波加热过程中物料升温特性的物理参数。

由式(5)和式(6)可知：微波加热中电场能和磁场能密切联系，变化的磁场产生电，变化的电场产生磁，变化的电磁场相互激励产生电磁波，波动过程在介电质中电磁能耗散直接转换为热能，进而提供加热物料的热源。同时，在电磁转化过程中，物料的介电系数、磁导率和电导率影响着物料与微波电磁场相互作用的效果。

1.2 电磁特性对热失控的影响

微波加热物料实质上是电磁场与物料相互作用的过程。物料温度升高导致介电损耗、电导损耗和磁损耗。对于本研究采用的碳化硅陶瓷固体，考虑其在加热过程中无明显磁化现象，忽略磁损耗的影响。在已有的文献中，微波加热陶瓷过程中大多只考虑陶瓷的介电损耗，本文根据碳化硅陶瓷的物理特性并结合陶瓷加热的特点，同时考虑介电损耗和电导损耗。

当微波与物料接触时，部分物料内部的极性分子在高频电磁波的作用下不断进行转向极化而发生碰撞、摩擦，从而将微波能转化为热能，实现物料的加热。在物料的极化损耗中，其吸收和转化微波能的能力可用复介电常数ε*表示，即

式中：ε′为介电常数，表示物料吸收微波的能力；ε″为介电损耗，表示物料将吸收的微波能进一步转化为热能的能力；j为虚数单位。根据热失控发生的机理，本研究重点考虑微波加热过程中介电损耗(ε″)对热失控的影响。

对于通过电导损耗产生热量实现加热的物料，在电场作用下将其吸收的电磁能量以传导电流的形式转化为热能。因此，在电导损耗中主要考虑物料电导率σ对加热的影响。

综合上述分析，考虑到热失控现象发生的难易，且研究所使用的陶瓷介质主要靠介电损耗和电导损耗来升温，在文献[23]与[24]中，使用指数函数模型[23]描述物料等效介电系数虚部与温度的关系，使用幂函数模型[24]描述电导率与温度的关系。因此，物料等效介电系数虚部ε″eff(θ)和电导率σ(θ)分别表示为：

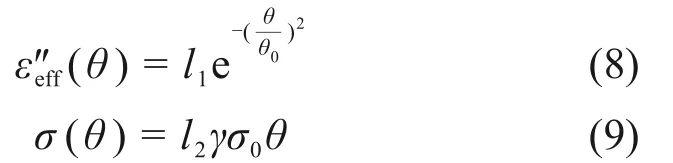
式中：σ0为真空中的电导率；θ0为峰值温度；γ，l1和l2为与介质物理性质、微波穿透深度、加热过程的初始条件和边界条件等有关的系数。

根据文献[25]，l1和l2可分别表示为：l1=其中：Rz为物料在z轴上的高度，即物料的厚度；θe为环境温度；ε(θe)和σ(θe)分别为环境温度下的介电系数和电导率。

2 热失控的尖点突变模型

2.1 微波加热热失控现象

通过能量守恒方程可以对热失控现象进行描述，故式(5)可表示为

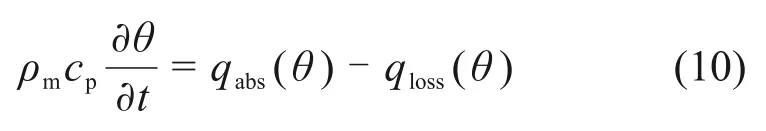
式中：qabs和qloss分别为产热量和散热量，表示微波加热系统能量的变化量。因此，在某个临界温度时产热大于散热(即qabs＞qloss)，若继续保持加热则会出现热失控现象。热失控可以描述为在加热过程中，微波与物料相互作用产生的热量远比散失的热量多，此时，物料温度急剧升高，为热失控的产生创造了条件。

刘长军等[26]基于FDTD 算法耦合求解Maxwell方程组和HTE 方程，完成微波加热陶瓷板的数值模拟，其结果与GUPTA 等[27]的结论基本一致。根据数值计算得到的陶瓷板中心稳态相对温度(相对温度其中，θ为物料温度，θh为常温)可知，温度随施加的微波功率不同呈现出S 形曲线变化趋势。通过分析由功率和温度组成的二维S 曲线可知，整条曲线分为上、中、下3 个部分。在上、下2个分支部分，温度与功率呈现一一对应的关系；在中间分支部分，同一功率下对应3个不同的温度点A1，A2和A3，表现为不稳定的状态。因此，温度急剧变化发生在曲线的中间分支。数值计算获取的S形曲线如图1所示。

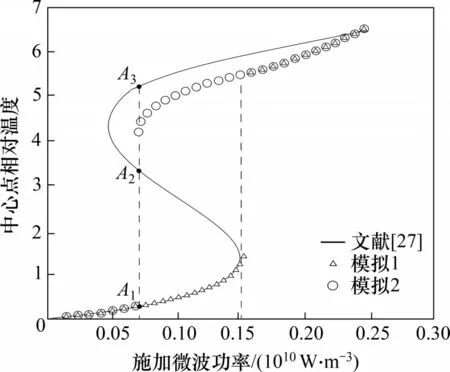
图1 微波加热过程S形曲线Fig.1 S-shaped curve of microwave heating process

由图1可知：采用响应曲面法可将二维的S曲线拓展为三维的S曲面。对于S曲面的研究，根据影响热失控的因素，并结合曲面特征可以将其用突变理论进行描述与研究。

2.2 微波加热能量分析

考虑微波加热过程中陶瓷固体介质通过介电损耗和电导损耗来实现快速加热。通过介电损耗产生的热量Q1表示为

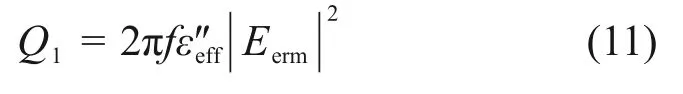
式中：f为微波源频率；|Eerm|为电场强度的均方根值[28]，为了方便后面计算，记|Eerm|为E。

通过电导损耗产生的热量Q2表示为

因此，结合式(10)可将微波加热过程中产生的总热量Q表示为

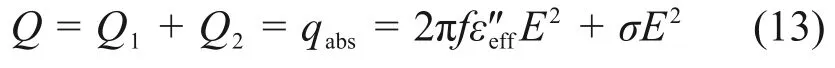
2.3 尖点突变模型

热失控是一种宏观表现为被加热物料温度发生急剧变化的突变现象，在此过程中涉及能量的聚集。当同种物质能量聚集到一定值时，其能量会发生从连续量变到突然质变的变化过程，即发生突变。在微波加热过程中，当微波能量在某一点富集到一定程度时，会使温度快速上升，即产生失控现象。能量在聚集过程中，往往会在一些突出点内富集，这些富集的突出点会发生尖点效应，从而产生更大突变，为物料发生热失控创造条件。因此，为了更好地定量研究热失控现象，本研究采用尖点突变理论来对温度变化进行研究，并通过尖点突变模型将热失控现象以数学表达式的形式定量呈现出来。利用尖点突变理论进行微波加热热失控分析的具体实现过程包括如下7 个步骤。

1)根据微波加热中物料吸收的总能量，建立加热系统尖点突变模型的势函数V(x)，并将其转化为如下尖点突变模型的标准形式：

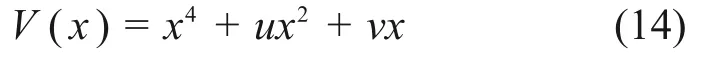
2)根据步骤1)所构造的势函数，对其状态变量x求一阶导数并令其值为0，即可得到平衡曲面M的方程：

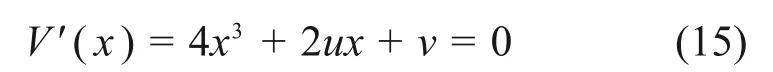
3)在步骤2)的基础上，再次求导，即可得到奇点集S的方程：

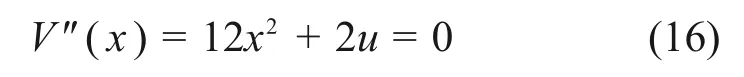
4)联立M和S的方程，消除x，即可得到突变的分叉集B的方程：

5)分析系统控制变量的变化情况并结合分叉集方程，可得微波加热过程中温度失稳的充要判据，即必要条件为u＜0，充分条件为Δ≤0。同时，分析突变过程状态变量的变化情况，可进一步推导得到热失控的临界温度表达式。

6)在COMSOL Multiphysics软件平台中建立微波加热SiC陶瓷介质的实验模型，加热一段时间并记录陶瓷介质的温度变化情况。根据陶瓷介质温度的分布、变化情况及获取的温度数据，结合步骤5)的稳定性充要判据及临界温度表达式即可判定系统的稳定性，并得到热失控临界温度。

7)根据稳定性判据和临界温度表达式及仿真加热过程的温度变化情况，对比验证尖点突变模型的有效性。

图2 所示为根据上述步骤构造的尖点突变模型。由图2 可见：由于系统状态会发生突变，因此，整个平衡曲面可分为上叶、中叶和下叶3个部分，状态变量x在控制变量u-v平面的投影Δ(即图中AOB围成的封闭区域)将整个控制变量空间分为稳定区域(即Δ＞0)和突变区域(即Δ≤0)，分别对应平衡曲面的上下叶部分和中叶部分。当x位于稳定区域时，系统在上叶或下叶发生平滑、稳定变化，而当x由上叶(或下叶)运动到下叶(或上叶)时，将不经过中叶，而是在上、下叶之间发生“跳跃”式变化，即系统状态发生突变。

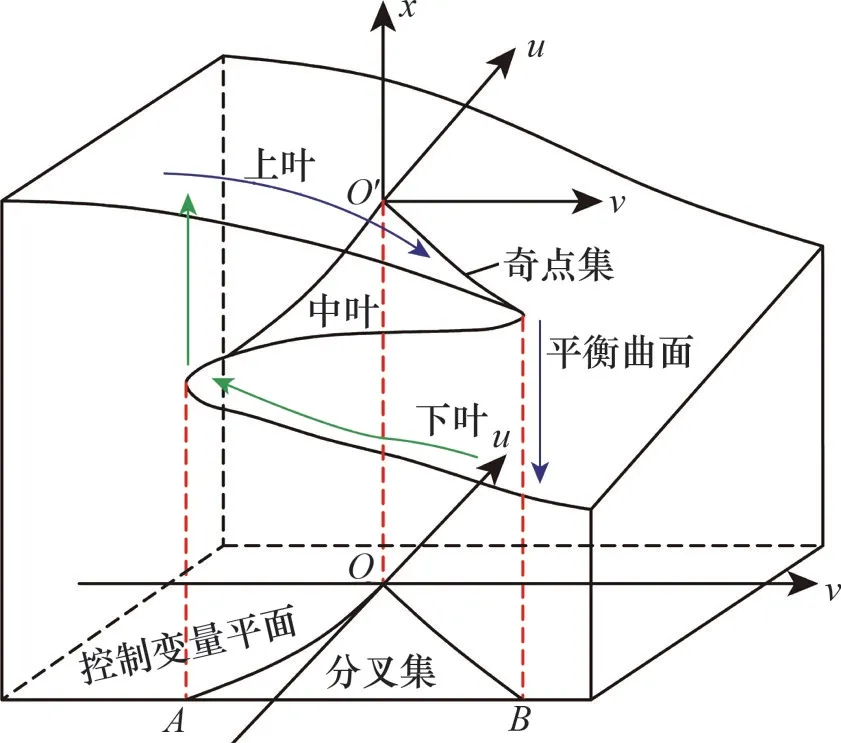
图2 尖点突变模型Fig.2 Cusp-catastrophe model

2.4 热失控发生的理论判据

本研究选择SiC陶瓷为加热物料，将加热过程中t时刻r处耗散的微波功率记为Q(r,t)，由式(13)可得

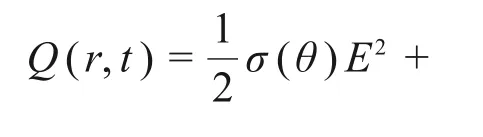
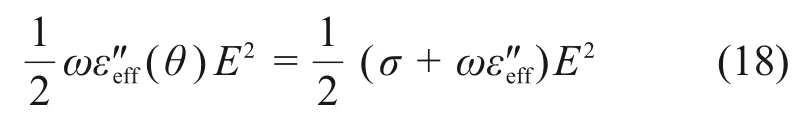
由突变理论可知系统状态的变化趋势可用势函数表示，结合式(8)和式(9)，则物料温度变化情况可表示为

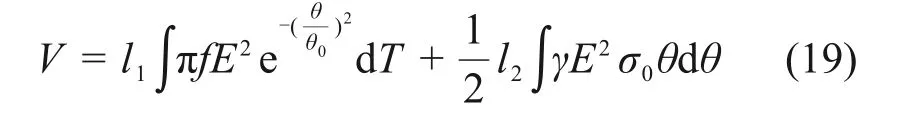
平衡曲面方程为

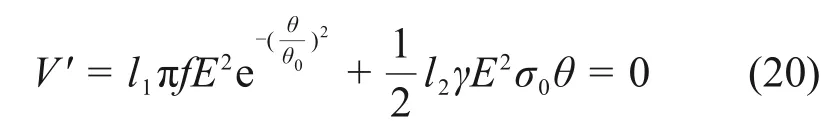
对平衡曲面进行二次求导可得尖点，即

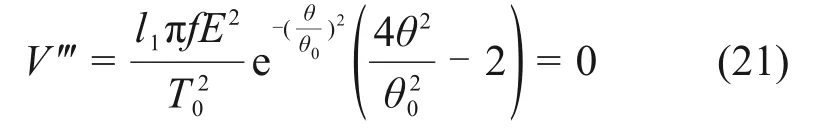
由式(21)可知，尖点处对应的物料温度可表示为

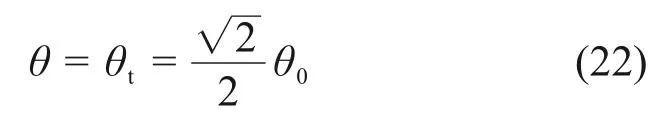
式(20)并不是标准形式，因此，需要将式(20)相对于尖点处的温度作Taylor展开，并截取至3次项，化简得

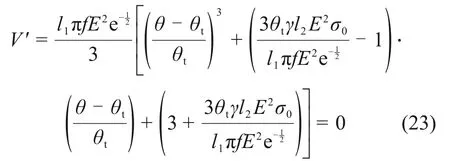
将式(23)进行变量代换，即可得到平衡曲面的标准形式：

式中：

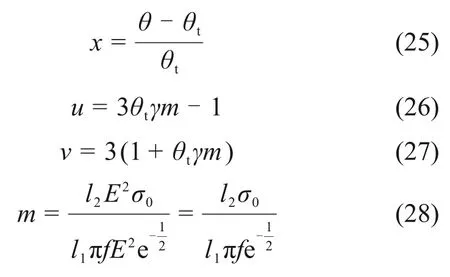
由式(28)可知，m与物料属性及微波加热的参数有关。联立式(26)和式(27)，即可得分叉集方程：

经过分析可知，式(26)和式(29)可作为判断加热过程的热稳定判据。结合图2可知，在热失控尖点突变模型中，只有当u≤0时，系统状态变量x才有可能与分岔集B相交，即发生突变。因而，发生突变的必要条件可表示为

式(24)为一个标准的一元三次方程，结合式(29)及方程的求根公式可知，当Δ= 0 且u＜0 时，状态变量x会产生突变，其温度变化率为：Δθ=因此，可得热失控临界温度表达式：

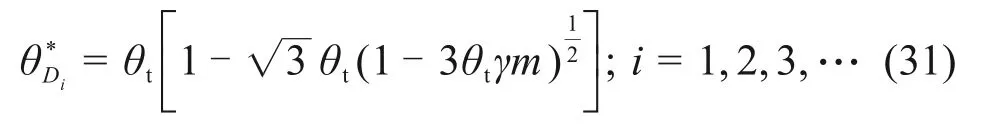
式中：Di为物料第i层临界温度点。

3 模型有限元分析

微波加热是一个复杂的物理过程，涉及电磁场、温度场等物理场的耦合，在该过程中介质温度的变化与系统几何模型、介质物理属性和介电特性等密切相关，呈现非线性、时变等特点，使用传统方式难以对其进行准确研究。有限元方法是一种广泛应用于解决复杂过程的数值计算方法，其基本思想是：在数值模拟软件中，通过离散化方法将整个求解对象划分为若干个小单元集合体，并根据小单元体的特性求解代数方程组，综合分析各个小单元体的解，最终即得到整个求解区域的近似解。为了研究微波加热过程固体物料温度的变化对系统稳定性的影响，本文采用有限元方法将整个复杂的物理求解域划分为若干微小的单元，通过研究各个小单元在加热过程中的温度变化情况，并综合分析即可近似得到整个物料的热力学性质。同时，在分析过程中考虑本构关系、初始条件、边界条件、介质的物理属性和电磁特性等对系统稳定性的影响。为了更好地进行数值模拟，选取第2节构造的尖点突变模型作为有限元分析的本构模型，并建立出微波加热碳化硅固体介质的几何模型。通过COMSOL Multiphysics软件平台，数值模拟出碳化硅陶瓷温度随时间的变化曲线，分析温升特性曲线并结合热稳定判据即可实现微波加热系统的稳定性分析。

在微波谐振腔中加热物料时，进行以下假设[29]。

假设1：加热介质陶瓷为均匀同质；

假设2：仅考虑z轴方向上的温度分布情况；

假设3：不考虑加热过程中物料体积变化和相变；

假设4：xOy平面电场分布均匀。

此外，在加热碳化硅陶瓷过程中，考虑到微波在谐振腔内不可能仅辐射于物料并被其完全吸收，将在腔体边界会发生一部分透射，故存在阻抗边界条件：

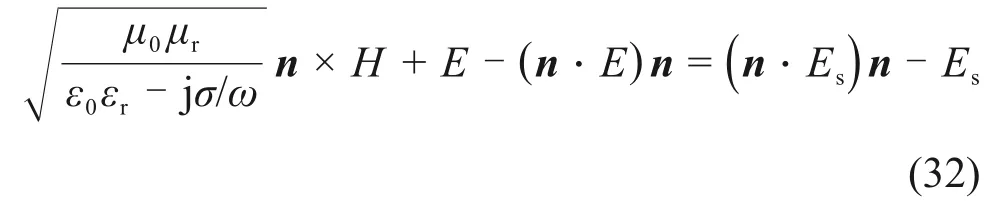
式中：μ0和ε0分别为真空磁导率、真空介电常数；μr和εr分别为相对磁导率、相对介电常数；ω为角频率；n为单位法向量。

3.1 几何模型

本文研究的微波加热陶瓷的几何模型如图3所示。模型主要由微波加热腔体、微波输入端口和加热物料组成。在加热过程中，馈口使用BJ-26波导馈入频率为2.45 GHz、功率为200 kW 的微波能量，微波谐振腔的长、宽、高分别为300，300 和200 mm，加热时间为340 s，腔壁为铜。被加热物料为正方体SiC 陶瓷片(边长为50 mm)，将SiC 陶瓷放置在一个绝热、不吸波、不反射波的“工”字形载物台上，且载物台长度、宽度、高度分别为80，40 和5 mm。为了实验结果的准确性，需对几何模型进行网格剖分，因此，本文定义最大单元边长为24.74 mm，最小单元边长为0.734 2 mm，网格划分结果如图4所示。

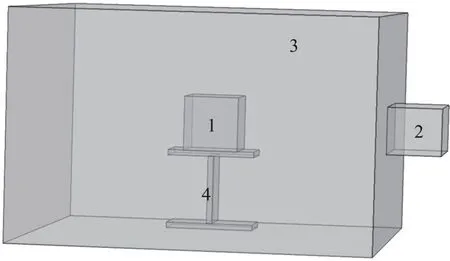
图3 微波加热系统几何模型Fig.3 Geometric model of microwave heating system

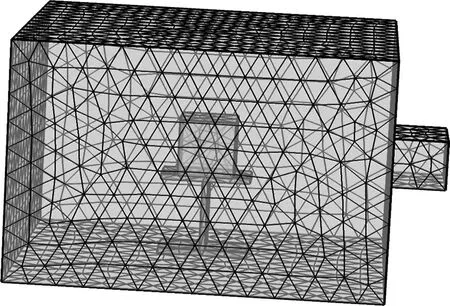
图4 加热系统模型网格划分Fig.4 Mesh generation of heating system

对于加热物料SiC 陶瓷， 在COMSOL Multiphysics 软件平台中进行仿真加热实验时，需要根据其介电参数及物理属性导入物料参数，从而进行仿真加热实验及有限元分析。SiC陶瓷的属性参数如表1所示[30-31]。

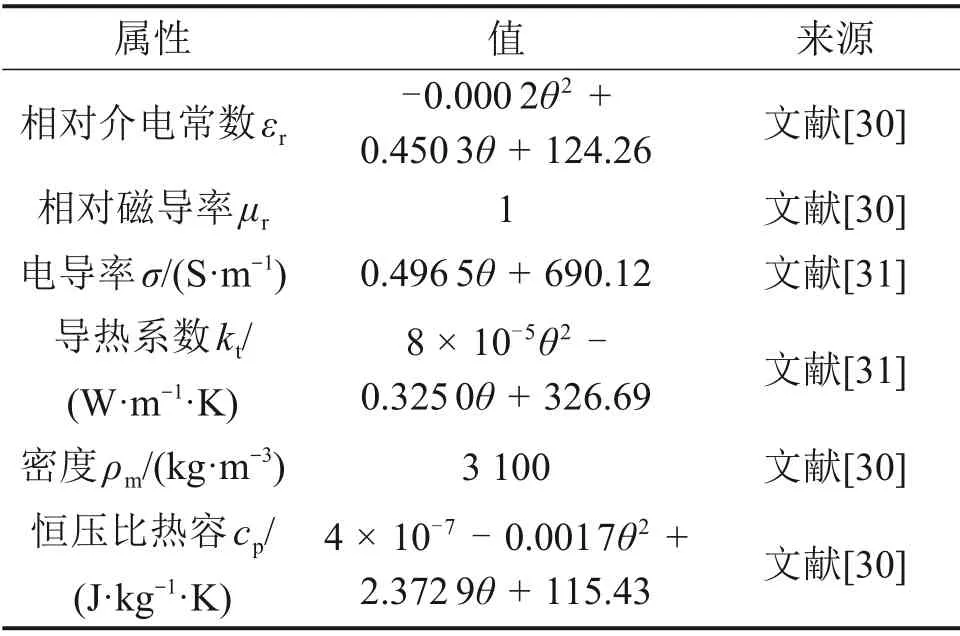
表1 数值模拟中所用材料属性Table 1 Properties of materials used in numerical simulation

3.2 模拟计算与结果分析

微波激励源频率为2.45 GHz，求解设定加热时间为0～340 s，通过数值计算可得陶瓷介质整体温升特性曲线如图5 所示。选取340 s 时的温度分布三维视图进行分析，如图6 所示。由图5 和图6可知：在开始阶段，陶瓷在微波电磁场作用下温度平稳升高，物料表面温度分布均匀，体现了微波均匀加热的特点。由于微波加热具有选择性加热的特点，物料不同部分、不同位置的温度分布逐渐呈现不均匀性，其中，上、下表面温度较高，而中间部分温度相对较低，这与物料对微波的吸收能力及微波的穿透深度等因素有关。

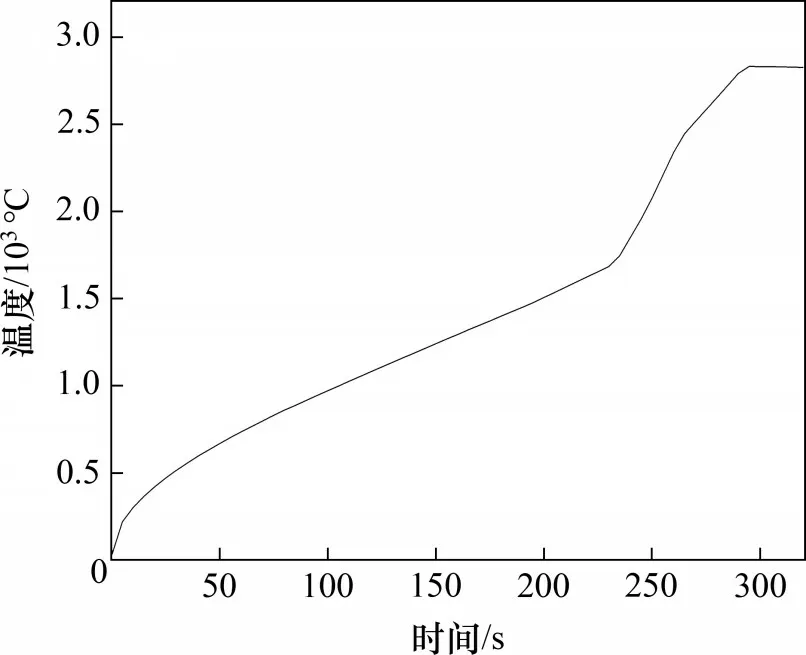
图5 碳化硅陶瓷整体升温特性曲线Fig.5 Overall temperature rise characteristic curve of SiC ceramic

图6 加热340 s时微波场内陶瓷表面温度分布Fig.6 Temperature distribution of ceramic surface in microwave field when heated for 340 s

本文选择截取加热时间为340 s 时，对物料上表面、中间截面及下表面进行研究，选取物料中心位置处作为坐标原点，3个截面的温度分布如图7 所示。此外，由于热失控表现为局部热点，因此，在3 个截面中分别选择点F1，F2和F3进行分析，其温升特性曲线如图8所示。

由图7和图8可知：在微波加热碳化硅陶瓷过程中，物料温度分布不均匀，上、下表面存在较为明显的热失控现象，表现为部分区域温度快速升高，而对于中间截面部分，温度呈现稳定上升趋势。

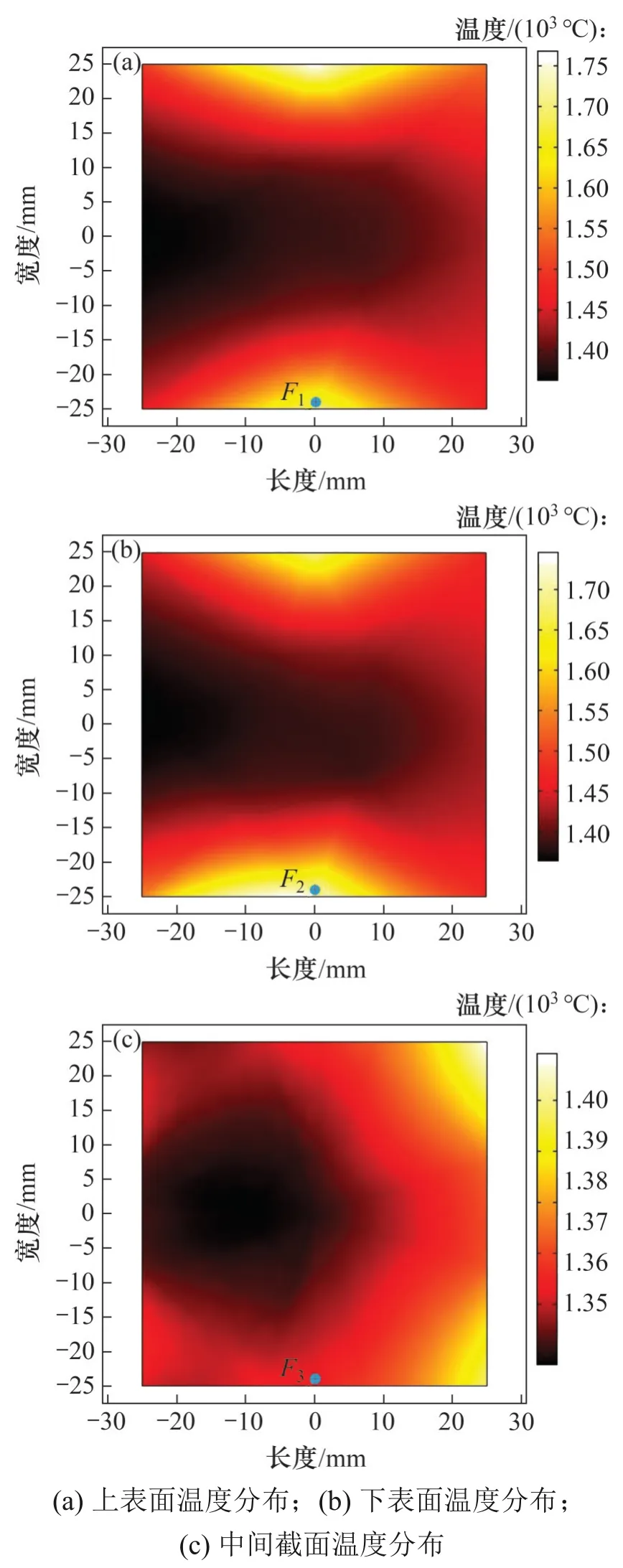
图7 340 s时3个截面的温度分布Fig.7 Temperature distributions of three cross sections at 340 s

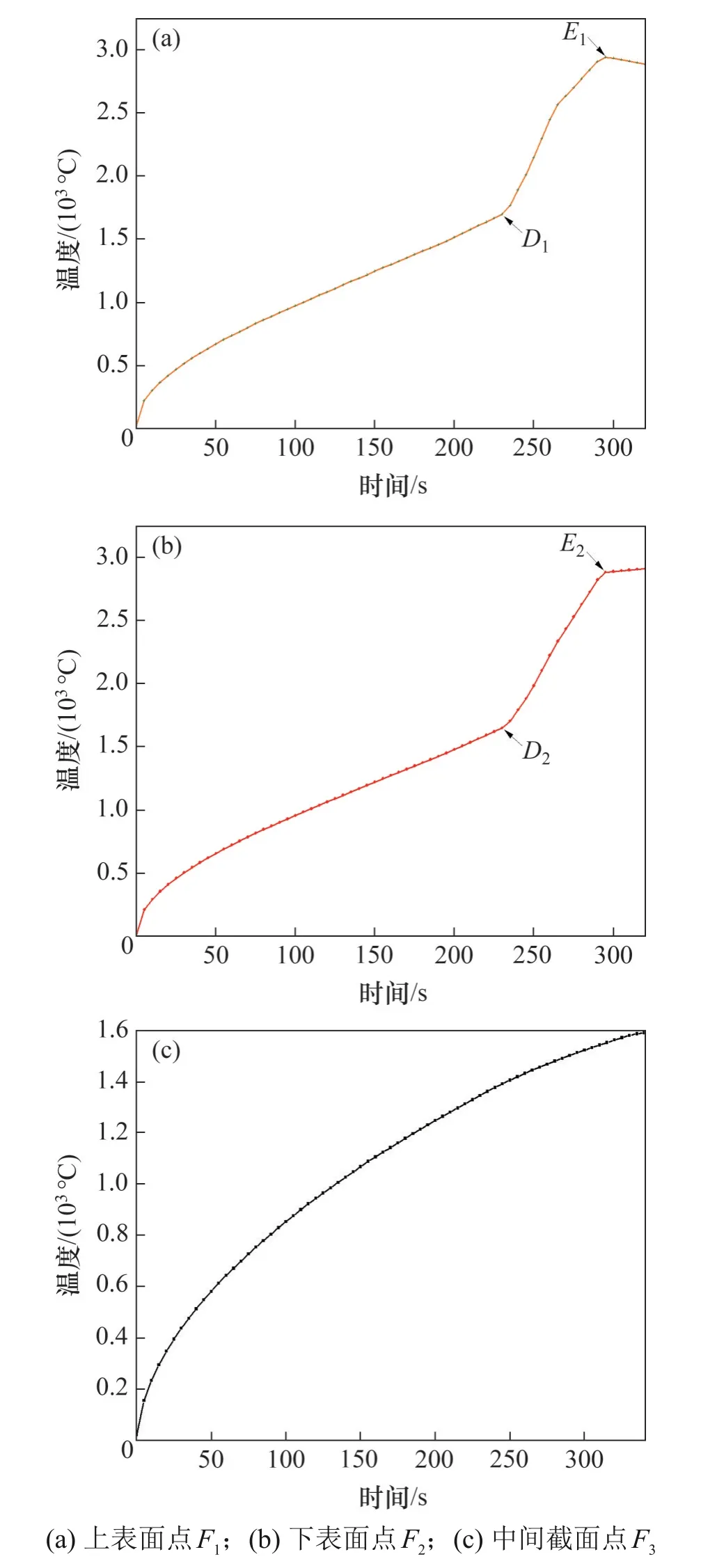
图8 3个截面选定点的温升特性曲线Fig.8 Temperature increase characteristic curves of selected point at three cross sections

记陶瓷板温升曲线温度发生急剧升高的点为Di，最高温度点为Ei，其中，i取1和2，则上、下截面Di温度分别为1 768 ℃和1 746 ℃。在COMSOL 仿真中，通过有限元分析考虑被加热物料的物理属性、微波穿透深度、系统初始条件和边界条件等，并结合文献[25]可知，微波加热SiC陶瓷时γ取-4，l1和l2的取值满足l2/l1=4.57×108是合理的。因此，可通过对截面定量分析来判断系统的稳定性。

对于上截面点F1而言，由温升特性曲线可知，从235 s开始，温度急剧上升，加热至295 s，温度出现最大值，即θ0=2 943 ℃，根据2.4 节，结合式(26)～(31)可知，u≈-5，Δ≈-475.0，由稳定性判据可知，u＜0，Δ＜0 时，发生热失控。根据第2节突变理论的相应推导，可通过式(21)，(27)和(31)得到此时热失控的临界温度，即

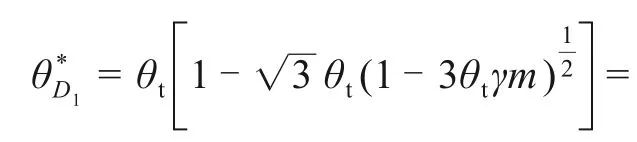
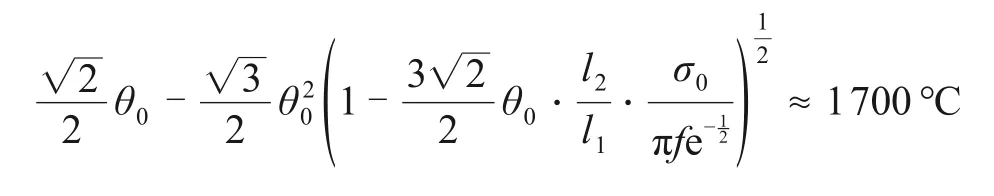
同理，对于下截面点F2，从235 s 开始，温度急剧上升，加热至295 s，温度出现最大值，即θ0=2 832 ℃，根据稳定性判据可知，u≈-4.84，Δ≈-472.6，此时存在热失控现象。相应地，此时热失控的临界温度表示为

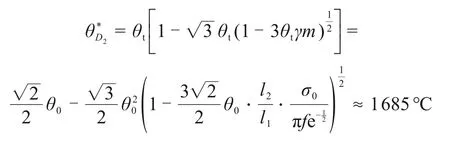
对于中间截面点F3，同样选择235 s 时的温度进行研究。 此时，u≈-2 ＜0，v≈1.5 ＞0，Δ≈28.8 ＞0，结合稳定性判据可知，没有发生热失控现象。

根据上述分析可知，温度数值计算结果与实验模拟结果中的点Di对应的温度接近，表明理论计算结果与有限元分析结果接近，通过尖点突变方法能对热失控现象进行定量研究。

4 结论

1)根据热失控的发生机理，通过对微波加热过程进行能量分析并结合加热介质的电磁特性及物理属性，构造出定量描述热失控现象的尖点突变模型。分析突变模型并推导得到判断加热稳定性的充要判据及临界温度表达式。

2)采用COMSOL Multiphysics软件平台构造微波加热SiC陶瓷的几何模型，综合考虑系统的初始条件、边界条件及物料的物理属性、微波穿透深度及电磁特性，可对陶瓷介质进行有限元分析。通过分析物料上表面、中间截面和下表面的温度分布情况及温升特性曲线，发现陶瓷上、下表面温度在235 s 时急剧上升，经过60 s 加热，温度分别从1 768 ℃和1 746 ℃升至稳定最高温度2 943 ℃和2 832 ℃，而中间截面温度稳定升高。

3)结合加热稳定性判据和临界温度表达式对加热过程进行定量分析可知，上、下表面Δ均小于0，分别为-475.0 和-472.6，u分别为-5.0 和-4.8，中间截面Δ为28.8，u为-2，说明物料在加热过程中温度分布不均匀，物料表面存在热失控现象，温升速率变化较大且温度相对较高，而中间温度升高较为平稳，温度相对较低。上、下表面临界温度分别为1 700 ℃和1 685 ℃，与有限元分析结果相吻合。定量分析结果验证了本研究提出的热失控尖点突变模型的有效性与可行性。