高速铁路Y型声屏障动态特性数值研究

吴小萍，朱烨，鲜凌霄，黄映凯，杜鹏程

(中南大学土木工程学院，湖南长沙，410083)

随着高速列车运行速度增加，其产生的噪声显著提高。研究表明，当列车速度达到300 km/h时，气动噪声将大于轮轨噪声成为首要噪声源[1]。声屏障作为降低铁路沿线噪声的重要措施，除承受自然风荷载之外，还会受到列车高速行驶通过时产生的脉动风荷载作用。当列车速度较高时，产生的脉动力对声屏障的作用效果更为明显，严重时会导致声屏障组件发生破坏从而影响行车安全[2]。2003年，德国科隆至法兰克福段高速铁路两边的金属插板式声屏障出现了铝合金单元板断裂、钢立柱与基座的连接螺栓松动等问题，为了保证行车安全，全线的金属插板式声屏障被拆除。声屏障的结构安全性与其动态性能密切相关，对其结构动力学性能进行研究具有重要的应用价值。人们对声屏障最初的研究主要集中在其降噪性能方面，随着列车速度提升，高速列车脉动风压问题逐渐受到普遍关注[3-4]。

国内外许多学者对声屏障的动态特性进行了大量试验研究和数值模拟研究。在试验研究方面，TOKUNAGA等[5-6]通过现场试验研究了高速列车通过声屏障时的空气动力特性，验证了数值模拟方法的可行性，并提出了2 种声屏障设计方法。LÜ等[7]从列车速度、列车类型等方面对声屏障的空气动力特性进行了试验研究，得到了不同参数的影响规律。在数值模拟方面，VITTOZZI 等[8]通过引入调谐质量阻尼器提出了解决结构振动的初步方案；LUO等[9]采用改进的延迟分离涡流模拟方法模拟了磁浮列车通过双侧声屏障时的气动性能，研究了声屏障高度和声屏障-列车距离等参数变化对流场的影响；卫星等[10]研究了封闭式声屏障在列车通过时所受脉动风压的特征规律；杨梦琦等[11]通过模态分析及瞬态动力学分析研究了不同工况下自然风与气动力作用下声屏障动力响应变化规律；罗文俊等[12-13]采用动网格法模拟了高铁进出声屏障全过程，得到声屏障各部位的脉动风荷载时程曲线及不同参数的影响规律，发现声屏障结构最大位移和最大应力随车速和立柱间距增大呈非线性增大。

上述关于声屏障的研究为高速铁路声屏障结构的优化设计提供了理论参考，但主要集中于直立型声屏障研究。Y型声屏障作为常见的声屏障类型之一，现有研究大都集中于如何提高降噪效果[14-17]，而忽略了其动力学性能研究。由于声屏障结构存在差异，在同等工况下，135°Y 型声屏障有效风压较直立型声屏障可增大4.6%[18]。为此，本文采用滑移网格方法模拟高速列车进出Y 型声屏障的全过程，研究不同折板角度(90°，105°，120°，135°，150°，165°和180°)、不同列车速度(300，350 和400 km/h)及不同声屏障-列车距离(3.6 m和4.0 m)等工况列车对声屏障的脉动风压规律，将其与声屏障有限元模型耦合进行瞬态动力学分析，得到声屏障的动态响应规律，并据此得到Y 型声屏障折板角的合理取值范围，以便为实际工程中Y 型声屏障的结构安全设计阶段提供技术支撑。

1 数值分析模型

1.1 列车-声屏障外流场模型

采用CRH380A 型高速列车，在保证其空气动力学的性能下，忽略列车的转向架、受电弓、车轮等精细结构，将列车简化成由光滑曲面构成的几何体。采用1 节头车、1 节中间车以及1 节尾车的3 编组列车模型[19]，模型总长为78.0 m，高为3.6 m，宽为3.4 m。Y型声屏障总长为200.0 m，高为3.0 m；折板长为0.5 m，宽为0.2 m。铁路、桥梁中屏障迎风面距离列车的距离通常为3.6 m 或4.0 m。为对比与其他类型声屏障的异同，将T 型(折板角90°)与直立型(折板角180°)声屏障加入计算。列车网格划分、列车与声屏障相对位置及不同折板角度声屏障示意图如图1所示。

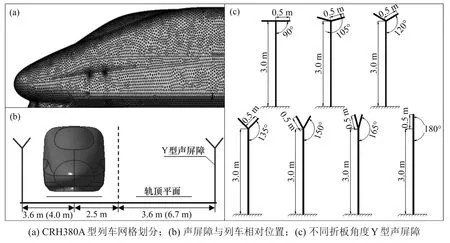
图1 模型及其参数示意图Fig.1 Schematic diagrams of model and its dimensional parameters

由于列车表面形状复杂，采用四面体非结构化网格划分，在车头车尾处进行局部网格加密，网格总数为800万个。高速列车与声屏障外流场计算域(长×宽×高)为300 m×50 m×30 m。列车表面、桥梁底面、声屏障等固体边界均设置为无滑移的壁面边界，计算域顶面、侧面设置为对称边界，计算域前后设置成压力为零的出口边界条件。

高速列车通过声屏障区域时，车头不断地压缩周围的空气，形成三维、黏性、可压缩的非稳态湍流场。采用标准k-ε双方程模型，相应控制方程如下：

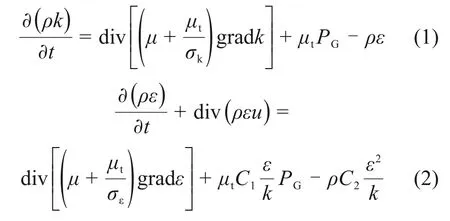
式中：k为湍动能；ρ为密度；ε为耗散率；t为时间；PG为湍动能产生项；μ为层流黏性系数，σε为湍流动能耗散率普朗特数；μt为湍流黏性系数；C1，C2，Cμ，σk和σε均为经验常数，一般取C1=1.44，C2=1.92，Cμ=0.09，σk=1.0，σε=1.3。

1.2 声屏障有限元模型

为对Y 型声屏障进行动力响应分析，建立有限元模型。将声屏障固体模型进行如下简化：将多孔的铝合金吸声板简化为表面无孔的封闭面板；声屏障单元板与立柱间的连接简化为由橡胶垫连接。本文建立20 m 长的声屏障有限元模型，共计10跨、11个立柱和10块铝合金复合吸声板。声屏障各构件的材料参数设置如表1所示。

表1 声屏障各构件的物理和力学参数Table 1 Physical and mechanical parameters of each component of sound barrier

1.3 模型验证

在模拟声屏障脉动风压与动态性能的过程中，不同计算方法与参数取值会对仿真结果产生一定影响。为此，以天津—秦皇岛客运专线某直立型声屏障区段为研究对象，采用上述计算方法和模拟参数建立相应列车脉动风数值分析模型，将车速为300 km/h 时的脉动压力仿真结果与实测结果进行对比[20]，结果如图2所示。

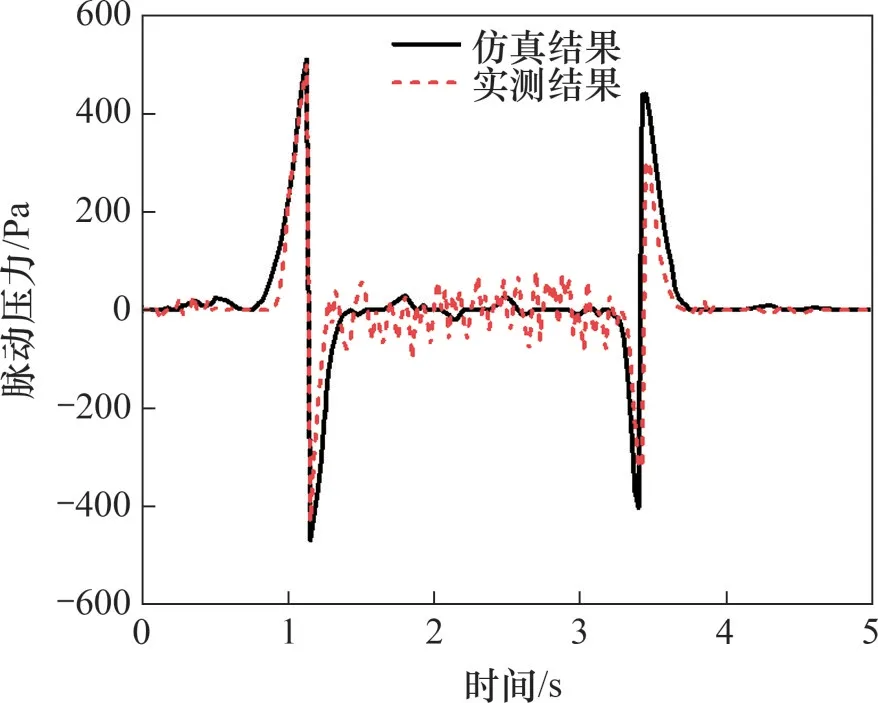
图2 脉动风压实测值与仿真值对比Fig.2 Comparison between measured and simulated aerodynamic impulse pressure

从图2可见：脉动压力仿真结果略大于实测结果，这是由于仿真模拟中将列车表面简化为光滑表面，削弱了风阻等作用。但这2条曲线的变化趋势基本一致，表明本文所采用的计算方法与参数能够较准确地模拟声屏障所受到的实际压力规律。

2 Y 型声屏障脉动风压仿真结果与分析

2.1 脉动风压分布规律

计算工况和结构参数不同，声屏障的脉动风压峰值也不同，但其变化趋势一致[12]。当列车速度为350 km/h，声屏障距列车为3.6 m 时，135°Y 型声屏障脉动风压时程曲线如图3(a)所示。从图3(a)可以看出：高速列车在通过Y 型声屏障区域的过程中，其压力波动与列车通过直立型声屏障时产生的波动趋势一致；在车头经过时，声屏障面板出现先正后负的脉动风压区；在车尾经过时，声屏障表面出现先负后正的脉动风压区，分别称为“头波”与“尾波”，并且“尾波”峰值明显小于“头波”峰值。

脉动风压峰值沿声屏障面板竖向分布如图3(b)所示。从图3(b)可见：在正压区沿声屏障高度方向，Y型声屏障的脉动风压变化规律为底部脉动风压最大，自下而上脉动风压先缓慢减小，在接近Y型折板区域时急剧降低，底部脉动风压约为顶部风压的1.77 倍。这是由于列车与声屏障间的空气受到挤压时，声屏障底部结构与地面连接，底部空气的外流场较封闭，空气流通速度小，而折板处空气与外部流场相流通，气流速度大，因此，声屏障底部脉动风压较大，沿着高度方向衰减，且越接近顶部，衰减越快。

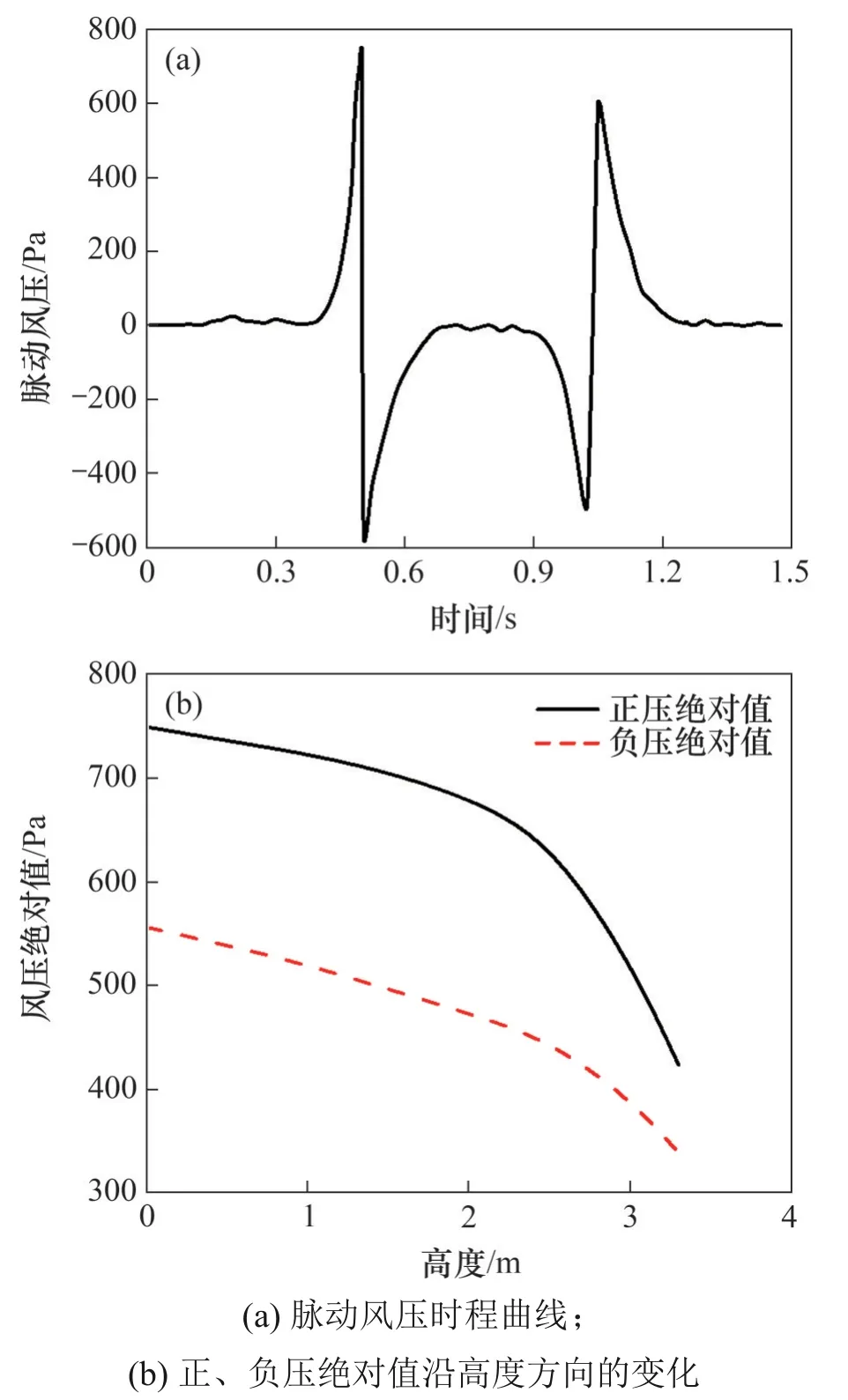
图3 列车通过Y型声屏障时的脉动风压Fig.3 Aerodynamic impulse pressure when train passes through Y-shaped sound barrier

2.2 不同参数下声屏障脉动风压影响规律

分析不同工况及结构参数下声屏障所受脉动风压的变化，车速分别取300，350 和400 km/h，声屏障-列车距离分别取3.6 m和4 m，弯折角度分别取90°，105°，120°，135°，150°，165°和180°。在不同车速、声屏障-列车距离和弯折角下，Y型声屏障脉动风压峰值变化曲线如图4所示。

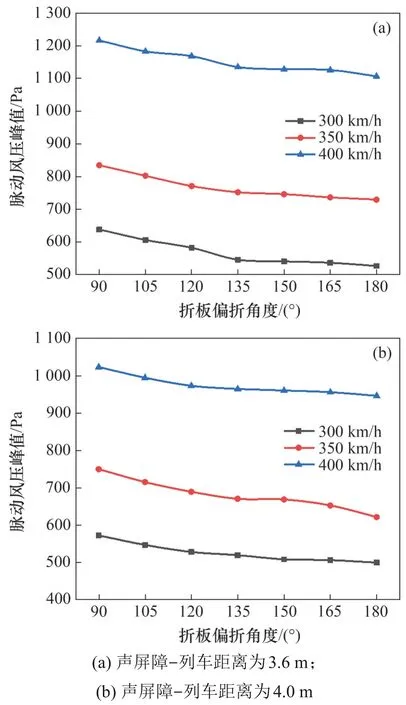
图4 不同参数下脉动风压峰值变化曲线Fig.4 Variation curves of peak aerodynamic impulse pressures under different parameters

2.2.1 列车车速对脉动风压峰值的影响

由图4 可知：当车速由300 km/h 增加至350 km/h时，T型、135°Y型、直立型声屏障所受脉动风压峰值分别增大30.8%，37.8%和38.4%；当车速由350 km/h增加至400 km/h时，3种声屏障所受脉动风压峰值分别增大45.7%，50.9% 和51.7%；随着列车速度增大，声屏障所受脉动风压峰值随之增大，且呈现出非线性加速增大的趋势。这是由于列车车速达到400 km/h 时，马赫数超过0.3，高速列车周围的流场将会出现从低速不可压缩流动向高速可压缩流动变化。

2.2.2 声屏障-列车距离对声屏障脉动风压峰值的影响

由图4 可知：声屏障-列车距离越大，列车与声屏障之间的空气流场越开放，其所受到的脉动风压越小；当列车速度为350 km/h 时，距列车4.0 m 的135°Y 型声屏障最大风压比距列车3.6 m的声屏障最大风压下降10.9%，T 型、直立型声屏障最大风压分别下降11.4%和17.4%。

2.2.3 声屏障折板角度对声屏障脉动风压峰值的影响

当声屏障折板角度在90°至135°之间变化时，声屏障面板脉动风压峰值逐渐降低；当折板角度在135°至180°之间变化时，脉动风压虽有降低的趋势，但变化幅度很小，逐渐趋于稳定；当折板角度为90°时，折板角度太小，导致声屏障与列车之间的流场相对较封闭，空气流通较弱，因此，此时脉动风压峰值最大；随着折板角度逐渐增大，折板与列车之间的开口越来越大，与列车之间的流场也逐渐开放，空气流通加强，因此，脉动风压的峰值开始逐渐降低。

以声屏障-轨道中心距3.6 m 时135°Y 型声屏障脉动风压最大值为基准，T型声屏障与直立型声屏障最大风压的相对差如表2 所示。从表2 可见：当车速为300 km/h时，T型、直立型声屏障最大风压相对Y 型分别增大16.9%和减小3.5%；当车速为350 km/h时，声屏障最大风压分别增大11.0%和减小2.9%；当车速为400 km/h 时，声屏障最大风压分别增大7.2%和减小2.4%。T 型、Y 型和直立型声屏障所受风压依次减小，随着车速增加，三者所受最大风压差距不断减小。

表2 3种型式声屏障的最大风压对比Table 2 Comparison of peak pressures of 3 types of sound barriers

3 Y型声屏障动态响应分析

3.1 模态分析

为检验高速铁路声屏障在列车通过的过程中是否发生共振，对声屏障结构进行模态分析。折板角度为135°的Y型声屏障前10阶振型云图如图5所示。

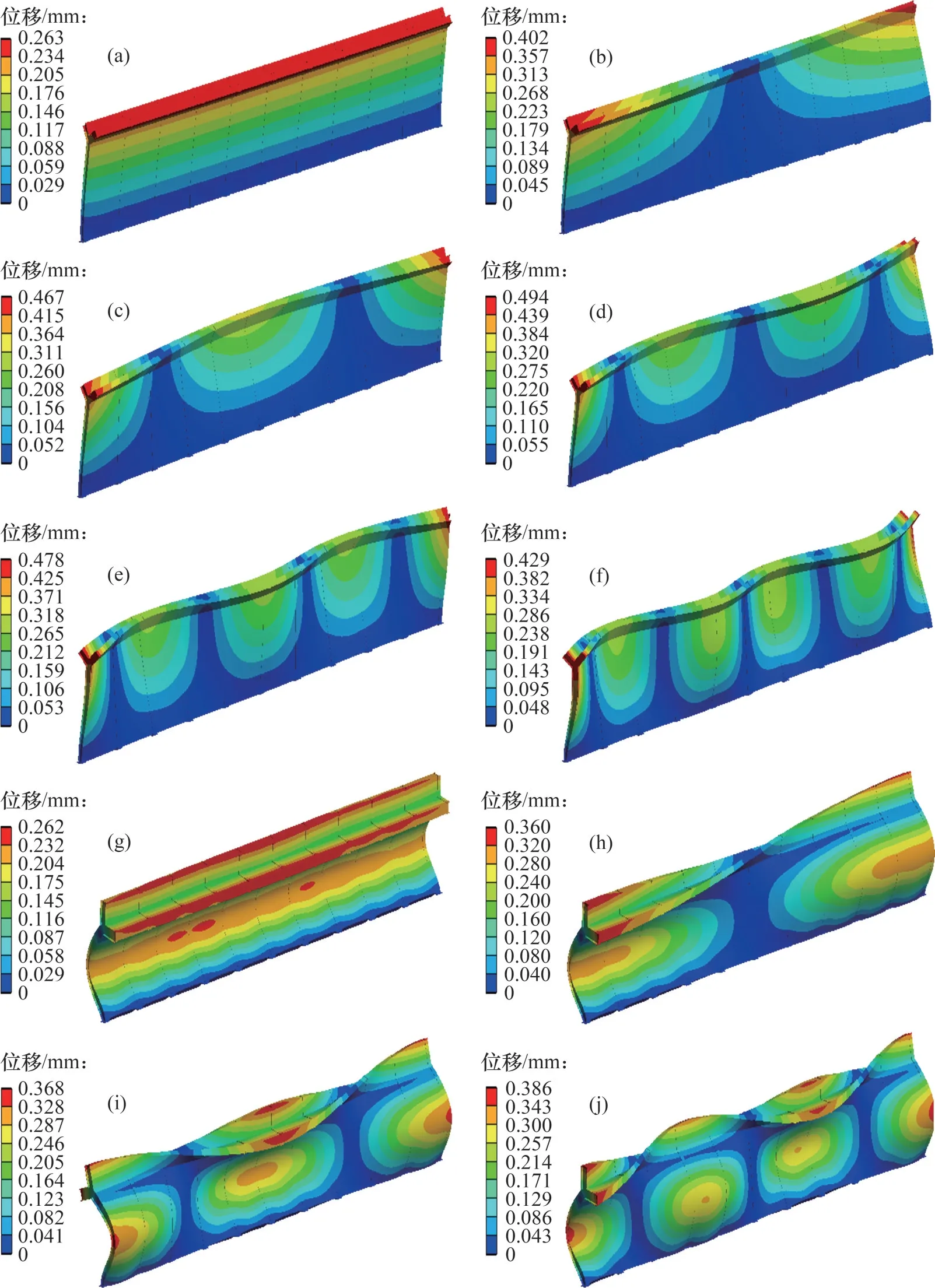
图5 135°Y型声屏障前10阶振型云图Fig.5 Cloud images of the front 10 modes of 135°Y-shaped sound barrier

从图5可以看出：第1阶振型主要是Y型声屏障整体结构的侧向弯曲；第2阶振型为立柱的扭转变形；第3 阶至第10 阶振型主要是折板结构及附近区域的扭转变形。声屏障振动的形状类似于弦曲线，在弦曲线的波峰处振动幅度最明显，Y型折板的振动幅度大于立柱和吸声板的振动幅度；振型越大，结构的振动幅度越大。不同类型、不同折板角度的声屏障前10阶模态振型基本一致。

不同折板角度声屏障前10 阶振型的固有频率如表3所示。由表3可知：各类型声屏障前10阶固有频率变化趋势基本一致，对于各阶固有频率，T型最大，Y型次之，直立型最小。以135°Y型声屏障基频为基准，T 型声屏障基频增加了21.3%，直立型声屏障基频减少了24.5%。改变折板角度对Y型声屏障的前2阶固有频率影响不大，但随着Y型声屏障折板角度增加，高阶固有频率呈现出显著变小趋势。这是由于立柱的扭转变形引起了相邻声屏障单元板的侧向振动。

由表3可以看出：声屏障一阶固有频率稳定在8～15 Hz之间，远比高速列车行驶过程中脉动压力的频率范围(2～4 Hz)大[12]，因此，声屏障结构在脉动风荷载下不会发生共振破坏。

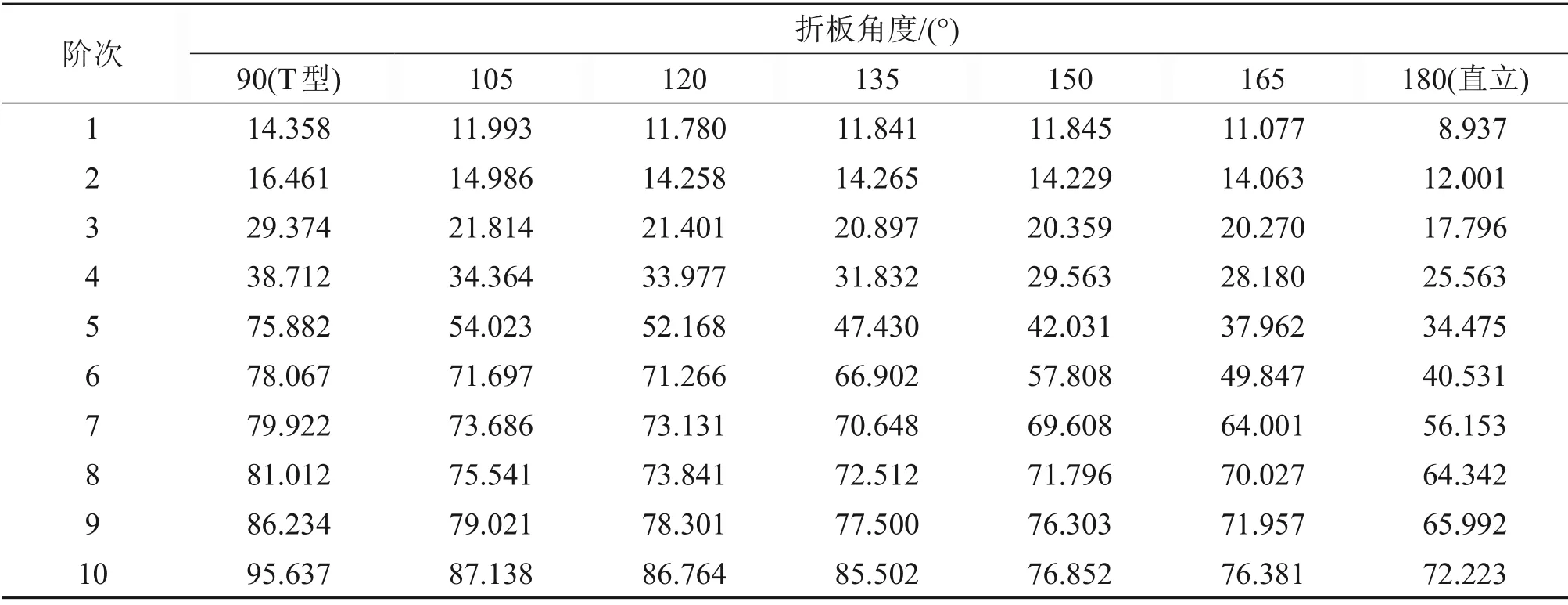
表3 不同折板角度的声屏障前10阶固有频率Table 3 The 1-10 natural frequencies of sound barrier with different folded plate angles Hz

3.2 瞬态动力学分析

将得到的声屏障脉动压力时程曲线加载至声屏障面板上，得到Y 型声屏障的瞬态动力响应曲线。图6所示为列车以350 km/h速度通过135°Y型声屏障时的最大变形时程曲线与最大等效应力时程曲线。从图6可见：声屏障的最大变形时程曲线和最大等效应力时程曲线与脉动风荷载时程曲线相吻合；在脉动风压的“头波”和“尾波”处，声屏障变形与等效应力响应曲线均达到峰值，最大等效应力为14.35 MPa，最大变形为1.03 mm。

图6 瞬态动力响应曲线Fig.6 Transient dynamic response curves

在不同车速、不同中心距下声屏障的变形与等效应力峰值有所差异，但其变化规律相同。在不同工况、不同类型下声屏障面板所受的最大等效应力和脉动压力如图7所示。从图7可见：随着折板角度增加，Y型声屏障的最大等效应力呈现出增大趋势，并且与脉动压力先下降后平缓的变化趋势不同，折板角度增加对Y 型声屏障的等效应力影响一直较大。这主要是由于声屏障实际高度随着折板角度增加而增大，声屏障整体结构的刚度减小，柔度增大，其受风压的影响作用也更大，从而使等效应力增大。

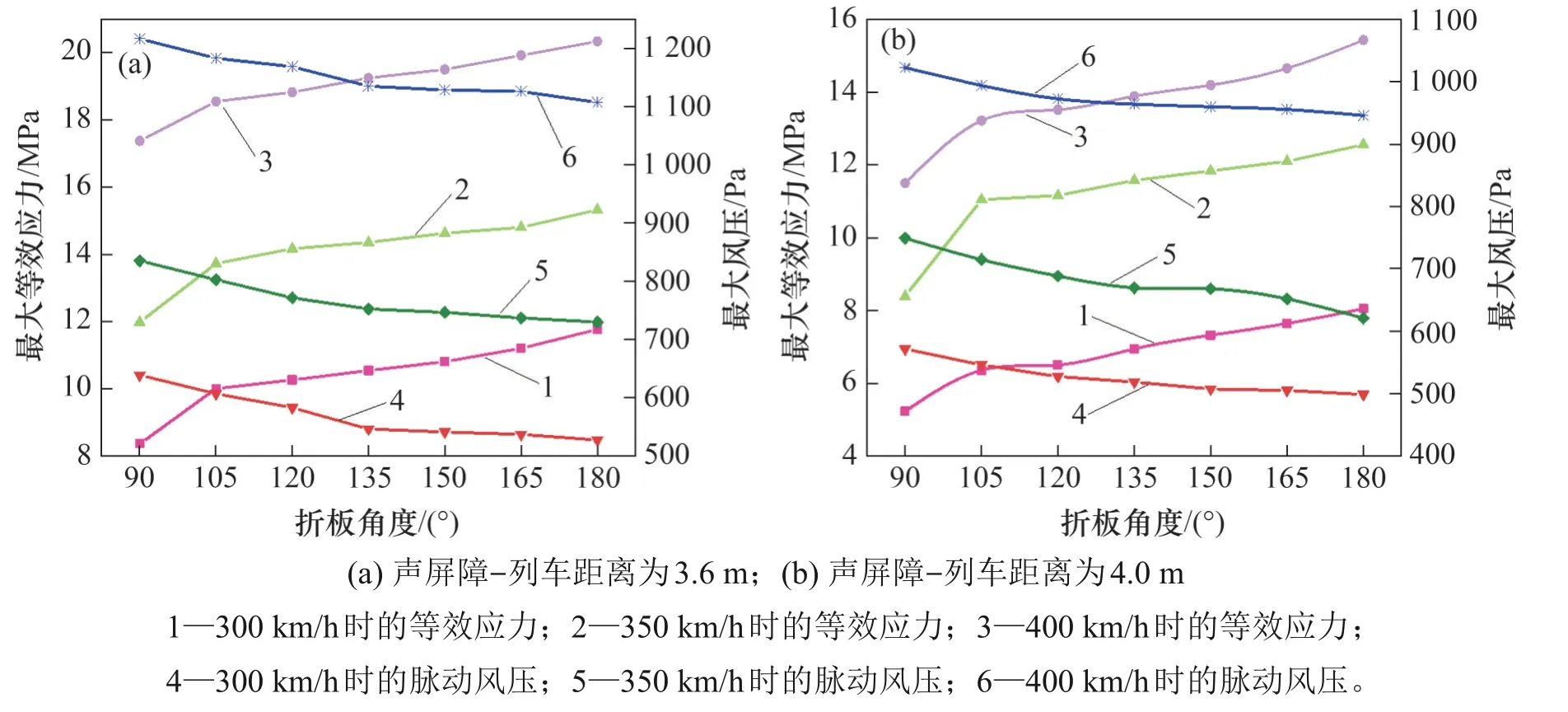
图7 不同工况、不同类型的声屏障面板所受的最大等效应力和脉动风压Fig.7 Peak equivalent stresses and aerodynamic impulse pressures on different types of sound barrier panels under different working conditions

由于折板角度增加对最大等效应力与脉动风压的影响规律相反，根据这2个指标对Y型声屏障折板角度进行优化。以T型声屏障为基准，在不同工况和折板角度下，Y型声屏障面板所受最大等效应力和脉动压力及其相对差如表4所示。对等效应力与脉动风压取相同权重，在各工况下，等效应力、脉动风压的相对差的矢量之和最小时的折板角度即为该工况时的最佳折板角度。

因此，当声屏障距线路中心线3.6 m，车速为300 km/h和350 km/h时，Y型声屏障最佳折板角度为135°；当车速为400 km/h 时，最佳折板角度为105°；当声屏障距线路中心线4 m，车速为300 km/h和350 km/h时，Y型声屏障最佳折板角度为120°；当车速为400 km/h 时，最佳折板角度为105°。因此，在实际工程中，在满足声屏障降噪性能的基础上，需选择较小角度Y 型声屏障(折板角度为105°～135°)。

4 结论

1) 当列车通过声屏障时，出现明显“头波”和“尾波”效应。沿高度方向，声屏障底部脉动风压最大，自下而上缓慢减小，在接近Y 型折板区域时开始急剧降低。

2)声屏障所受脉动风压峰值随着列车速度的增大呈非线性加速增大，随声屏障至列车距离增加而减小，随折板角度增加而降低。不同类型声屏障脉动风压峰值存在明显差异，T型的脉动风压峰值最大，Y型的次之，直立型的最小。

3)折板角度增加对Y型声屏障基频影响不大，但高阶固有频率随折板角度增大而减小。各类型声屏障结构基频集中于8～15 Hz，均大于高速列车脉动压力频率，不会发生共振破坏。

4)声屏障的最大变形、等效应力时程曲线在脉动风压“头波”和“尾波”处出现峰值；但最大等效应力随着折板角度增加而增大，其变化趋势与脉动风压的变化趋势相反。综合声屏障等效应力与脉动风压变化规律，在实际工程中，需选择小折板角度(105°～135°)Y型声屏障。

5)在列车脉动风作用下，声屏障的最大风压出现在其结构底部，因此，应对钢立柱底部与加劲板焊接处采取措施进行加固并加强监测。同时，列车速度对声屏障脉动风压影响明显，在声屏障区域，适当降速可延长声屏障使用寿命。